基于可變模糊理論的建筑工程造價估算研究
張如好 柳裕政
(1.江蘇天舜建設有限公司,江蘇 淮安 223003; 2.淮陰工學院,江蘇 淮安 223003)
在我國,傳統工程項目主要是通過施工圖預算和最后的竣工決算來進行工程造價控制,一方面工程造價需要在設計圖紙基本完成之后,而且工作量巨大,一旦圖紙變更,造價工作又要重頭再來;另一方面在工程初期,項目建議書和可行性研究階段,決策者十分重視投資估算,此時由于缺少必要資料傳統造價方法難以運用。隨著經濟建設的高速發展,建設項目的全壽命周期概念的提出,工程計價貫穿于建設項目各個階段,在工程項目前期很難根據傳統的定額計價和清單計價確定出一個合理、正確、科學的造價。因此工程投資估算作為工程造價中的第一個環節,其地位在與日遞增。
由于建筑項目各階段的造價指標不同,其工程造價的內容和方法也有許多種。施工圖設計階段的預算和竣工階段的決算往往都是清晰明確的,相比而言項目建議書和可行性研究階段的投資估算和初步設計階段的概算具有明顯的模糊性、灰色性,因此很多學者將模糊數學、灰色預測模型、大數據和智能算法等方法應用于工程造價估計,顯著的減少了計算周期,在工程項目前期為決策管理者提供了有效的途徑和有力的支撐。工程造價估算影響因子眾多,如何在眾多的因子中選取最相關的因子并計算多因子對目標的隸屬度是問題的關鍵,而可變模糊集理論在計算多因子對目標隸屬度上具有獨特的理論與模型優勢,已經在多領域類似問題上得到廣泛的應用。
1 可變模糊集理論簡介

(1)
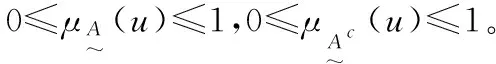
令:

(2)

(3)


2 基于可變模糊集理論的建筑工程造價估算模型
2.1 指標體系選取和歸一化處理
假設已建工程A和擬建工程B的指標體系分別為a和b,二者組成指標體系向量組xij,由于建筑工程不同指標的單位數量級差異較大,在同一模型中無法進行數值計算,首先要對指標體系進行歸一化處理。本文中對指標數值越大,造價越高的指標采用式(4)進行處理,對指標數值越大,造價越低的指標選用式(5)。歸一化后的指標體系在數值上統一可比對,即指標數值越大,工程造價越高。
(4)
(5)
2.2 層次分析法確定指標權重
對建立的指標體系采用9標度法,將多指標的重要性比較簡化為多層次的兩兩比較,構建判斷矩陣,從高層到底層計算判斷矩陣的特征根,并檢驗一致性,最后求出各指標對目標層的權重,即求出指標“重要性”權重w。
w=(w,w,…,wm)=Wi。

2.3 可變模糊估算模型
應用兩級模糊優選模型,得到已建工程和擬建工程各指標的對造價綜合貢獻相對隸屬度uj:
(6)
其中,uj為相對隸屬度;α為模型優化準則參數,α=1,2分別為最小一、二乘方準則;p為距離參數,通常可取為海明距離p=1,歐氏距離p=2。
已知已建工程的造價為S,擬建工程的造價S0為:
S0=S×uB/uA
(7)
3 實例與比較分析
3.1 工程基本特征
隨著經濟社會和城鎮化的快速發展,城市多個商圈模式凸顯其交通和區位優勢,高層建筑作為商圈的核心,其造價估算在區域用地規劃中的意義十分重大,造價估算的準確性直接影響項目建議書和可行性研究報告的編制,甚至決定項目能否落地,按計劃和設想發揮其區域帶動力。本文以某一高層建筑單方造價估算為實例進行研究,已知兩棟高層建筑已建工程A和擬建工程B的基本建筑信息情況如表1所示。

表1 已建工程A和擬建工程B的工程特征
工程造價的估算,涉及因素很多,建筑本身的設計、用途、材料、價格直接影響造價,同時施工企業的技術水平、管理水平、天氣、物價波動等間接因素也對工程造價產生一定影響。根據高層建筑特點,選擇最相關的因子建筑面積、層數、檐高、底下深度四個參數作為造價估算指標體系。
3.2 建筑工程造價估算
對指標體系進行歸一化處理后,采用可變模糊估算模型分別計算已建工程和擬建工程對造價的隸屬度uA=0.53和uB=0.47,已建工程的造價S為1 516.75元,則擬建工程的單方造價S0為1 363.42元。
將估算所得數值與建筑工程項目建成后的實際工程造價進行對比,進而驗證準確度,如表2所示。

表2 基于可變模糊集理論的建筑工程造價估算模型驗證結果
4 結語
由于工程項目規模大,耗費大量人力物力財力,工程項目造價也很大,同時不同類型工程項目,造價也各不相同,且隨著建設周期的推移,工程造價也具有動態性。工程造價遍布于建設周期的各個階段,不同階段諸如項目建議書中的投資估算、初步設計階段的概算和施工圖設計的預算及最后的竣工決算,是一個逐步深化的過程,不同階段的工程造價內容、含義和方法均不相同。
隨著建筑工程全過程、全生命周期的概念被引入到建筑工程規劃、設計、施工、運行中,在工程項目可行性研究階段就需要對擬建工程進行合理、正確、科學的造價估算,針對工程造價估算的非線性、動態性和模糊性,提出了一種基于可變模糊理論的建筑工程造價估算模型,可以在相似已建工程的基礎上,對尚未進行施工圖設計的擬建工程造價進行有效的估算,方法簡單有效,可為項目建議書可行性研究中的項目投資估算提供有效的支撐,隨著建筑信息云數據和云平臺的應用,該方法的優勢將得到更好的體現。

