基于特征基函數法的一維理想導體粗糙海面電磁散射快速算法研究

王晶晶 王安琪 蔣鐵珍 黃志祥

(安徽大學 計算智能與信號處理重點實驗室,合肥 230039)

引 言

粗糙海面電磁散射特性的研究在現代雷達探測、海洋探測、目標隱身等領域有著廣泛的應用[1-3]. 近年來有關該問題的研究受到國內外諸多學者的關注,如有限元積分方法在海面電磁散射中的應用[4],雙尺度法在海面電磁散射中的應用[5]等. 而矩量法[6](method of moments, MoM)因其自動滿足輻射條件、無需額外設置邊界條件、計算精度高等優點被廣泛應用于粗糙海面電磁散射的數值仿真中[7-11]. 然而MoM中的矩陣通常是一個滿陣,當求解具有較多未知量的矩陣方程時存在對計算機內存需求過大、計算耗時的缺點. 尤其是當利用MoM仿真模擬大角度入射下粗糙海面的電磁散射問題時,必須模擬足夠長的粗糙海面[12]才能保證計算結果的精確性,這必會引入大量的未知量,對計算機內存的需求過大. 因而尋找一種精確快速計算粗糙海面電磁散射的數值方法就非常必要了.

為克服因計算量大而導致的計算機內存負擔過重的缺陷,前人在傳統MoM的基礎上做了一些改進,相繼提出了一些高效的算法,如快速多極子法[13]、預修正多層快速多極子算法[14]等,然而這些方法是采用一定程度的近似從矩陣方程生成的角度或者結合預處理技術加快迭代收斂過程對MoM方法進行改進,存在迭代收斂的缺陷,導致高海情粗糙海面電磁散射數值仿真時存在迭代步數過多、計算時間過長的困境.

本文應用的特征基函數法(characteristic basis function method, CBFM)最初是由Mittra和Prakash提出的[15],基于子域的概念,根據Foldy-Lax多徑散射方程[16]構造特征基函數,通過離散子域尺寸的選取控制實際操作矩陣的維數. 它可以在保證計算精度的前提下,有效地縮短計算時間,同時降低對計算機內存的需求.

1 粗糙海面電磁散射的MoM研究

圖1為一維理想導體(perfectly electric conductor, PEC)粗糙海面電磁散射的幾何示意圖,其中粗糙海面是PM(Pierson-Moskowitz)譜海面[17],高度函數為z=f(x). 模擬粗糙海面的長度為L,海面風速為U. 本文中所采用的時諧因子是e-iωt,位置矢量為r=xx+zz. 當入射電磁波是水平(Horizontal, H)極化方式時,其電場積分方程(electric field integral equation, EFIE)為[16]

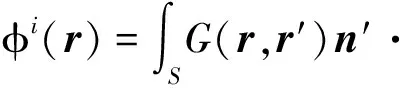
(1)

當入射電磁波是垂直(Vertical, V)極化方式時,粗糙海面的磁場積分方程(magnetic field integral equation, MFIE)為[16]

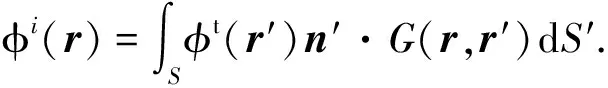
(2)

式(1)、(2)中:

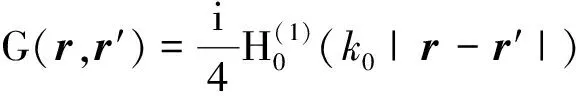
(3)

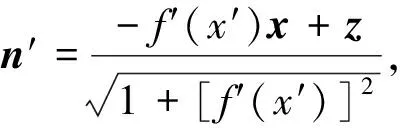
(4)

f′(x′)是高度起伏函數f(x′)的一階導數.

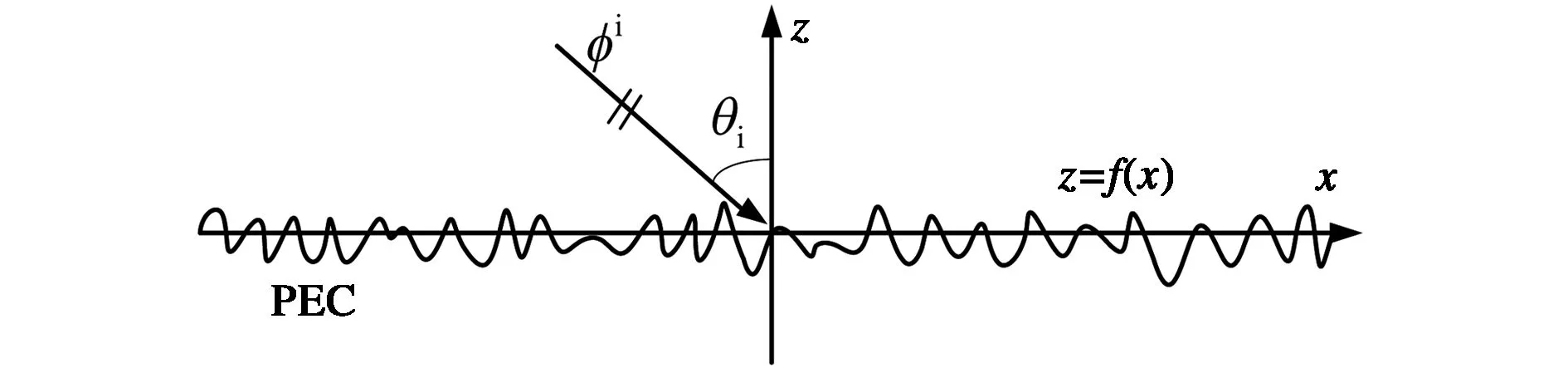
圖1 一維理想導體粗糙海面電磁散射的幾何示意圖Fig.1 Geometric model for EM scattering from the 1D PEC rough sea surface

為避免因模擬粗糙海面尺寸的有限造成的截斷效應,本文采用錐形波作為入射波,即[12]

φi(r)= exp(ik(xsinθi-zcosθi)(1+w(r)))

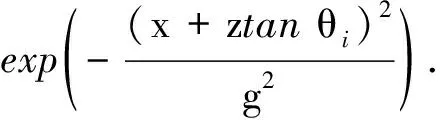
(5)

式中:k是入射波的波數;θi表示入射角;g是錐形波因子;w(r)=[2(x+ztanθi)2/g2-1]/(kgcosθi)2.

在MoM中,分別選取分域脈沖基函數和點匹配技術離散式(1)和式(2)的積分方程. 當H極化入射時對EFIE離散,得到相應的矩陣方程為[16]

A·U=b.

(6)

同樣可以得到V極化波入射下,MFIE離散后的矩陣方程為[16]

B·I=V.

(7)

式(6)與式(7)的具體形式可參考文獻[16].

2 CBFM的數學原理

通過分析,可將式(6)和式(7)轉化為同一類矩陣方程,形如

Z·J=V.

(8)

式中:Z是N×N的阻抗矩陣;V是N×1的激勵向量;J是N×1的未知向量;N是未知量的個數. 由于阻抗矩陣Z通常是滿陣,當處理大角度入射下理想導體粗糙海面電磁散射問題時[12],必須模擬足夠長的粗糙海面才能保證計算結果的有效性,這必會導致較多未知量的產生,會遇到所需計算機內存過大、計算時間過長的問題. 而CBFM很好地解決了這一問題. 下面介紹CBFM的數學原理.

首先將N個離散點的粗糙海面劃分為M個子域或塊,每個子域包含的離散點數是Ni(i=1,2,…,M),且滿足N1+N2+…+NM=N,則式(8)可變為如下形式[18]:

(9)

式中:Zij(i=1,2,…,M;j=1,2,…,M)是Ni×Nj的矩陣;Ji表示需要求解的未知量;Vi表示粗糙海面受到的與入射電磁波相關的激勵向量. 本文的特征基函數(characteristic basis functions, CBFs)是根據Foldy-Lax多徑散射方程[16]構造的,包括主要特征基函數(primary characteristic basis functions, PCBFs)和次要特征基函數(secondary characteristic basis functions, SCBFs). 構造CBFs時,先不考慮子域與子域之間的互耦效應,只考慮每個子域的自相互作用構造PCBFs,再將除了該子域外的所有PCBFs對該子域產生的散射場之和作為此子域第一階SCBFs的激勵源,這樣依次進行高階SCBFs運算,最后由PCBFs和SCBFs的加權疊加構造CBFs. 構造CBFs的詳細過程如下:

1) PCBFsJP

對于第i個子域(i=1,2,…,M),其PCBFs滿足

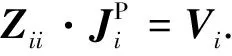
(10)

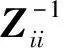
2) SCBFsJS1,JS2,…

用來求解子域i的第n階SCBFsJSn的激勵可由除該子域i外所有其他子域上的前一階的SCBFs對其產生的散射場得到,即JSn滿足

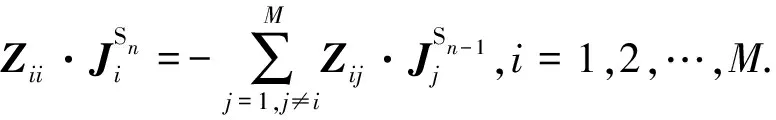
(11)

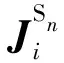
3) CBFsJt

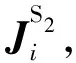
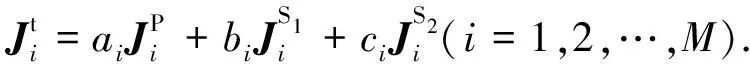
(12)

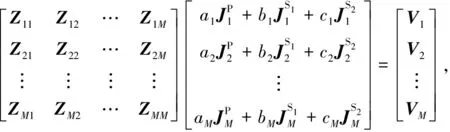
(13)

即

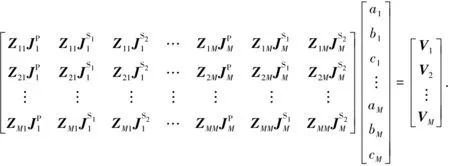
(14)

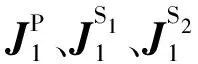
(15)

對式(15)的系數矩陣進行LU分解后求逆可獲得疊加系數ai、bi、ci(i=1,2,…,M),將其代入到式(12)中,可以求得待求表面未知量Jt.

本文中定義CBFM的計算誤差為[19]

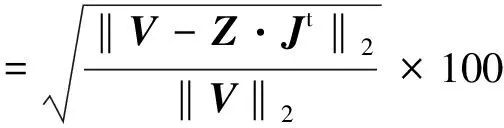
(16)

式中,‖·‖2表示矩陣的二范數.

3 數值計算與結果分析

3.1 算法有效性的驗證

為驗證所提算法的有效性,本文將針對一維理想導體粗糙海面電磁散射的仿真計算分別采用文中所提的算法(CBFM)、基于LU分解技術的MoM (MoM-LU)、基于共軛梯度法的MoM (MoM-CGM),以及快速多極子方法(fast multiple method, FMM). 圖2給出了H極化波和V極化波入射下四種方法的散射系數對比,表1給出了分別采用上述四種方法的計算時間. 粗糙海面模型的參數選擇如下:海面是PM譜海面,風速分別為U=5 m/s(圖2)和U=10 m/s(圖3),入射角分別為θi=45°(圖2)和θi=60°(圖3),模擬海面長度L=81.92 m,采樣間隔Δx=0.1λ,入射波頻率選擇f=1.5 GHz,即可得采用傳統MoM時的未知量個數N=4 096,CBFM算法中選擇了4階SCBFs和8個離散子域. 算例執行的軟、硬件條件為Intel(R) Core(TM) i7-6700 CPU @ 3.41 GHz,內存4.00 GB,操作系統Microsoft Windows 10,軟件環境Intel Visual Fortran 14.0,時間為總的CPU時間. 從圖2可以明顯地看出,本文所提算法CBFM的計算結果與另外三種方法吻合的是比較好的,說明了文中所提算法的精確性．

(a) H極化(a) H polarization

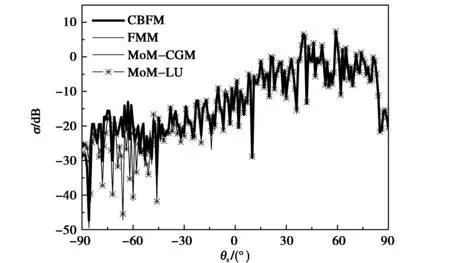
(b) V極化(b) V polarization圖2 H和V極化入射時散射系數對比Fig.2 The scattering coefficient obtained by different method under the H polarization and V polarization

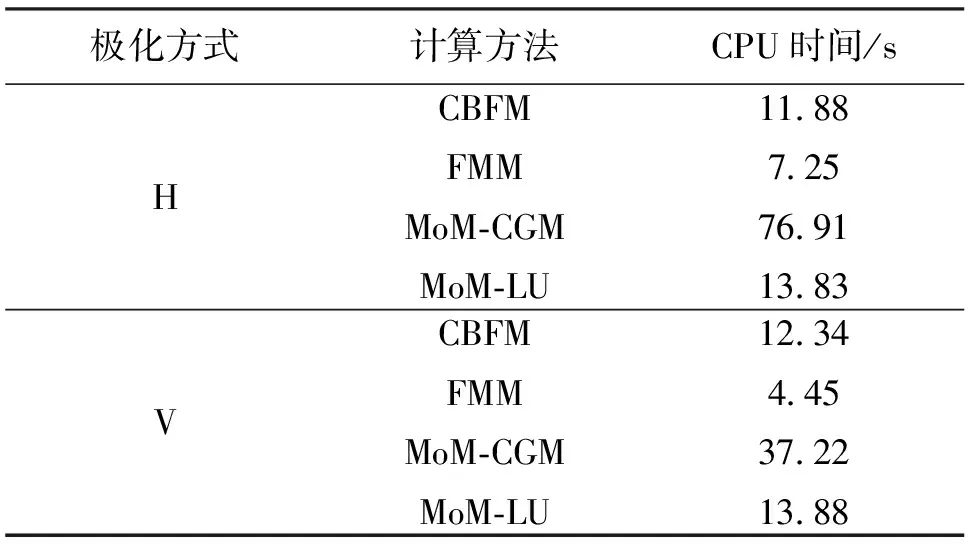
表1 不同計算方法的CPU時間Tab.1 The CPU time of different methods

從表1可以看出本文所提算法明顯地減少了MoM的計算時間,尤其是采用迭代方法的MoM. 在此需要指出的是本文所提的算法慢于FMM,這是因為在FMM中引入了加法原理,但FMM將MoM中的稠密矩陣處理為了幾個對角矩陣,且這一處理過程的數學公式較為復雜,仿真實現比較困難. 而文中所提算法是直接對MoM中的稠密矩陣進行分塊處理,并結合具體的物理機理(Foldy-Lax多徑散射方程),數學公式簡單明了,仿真實現也是比較方便的. 另外,FMM是基于迭代法實現的,受到矩陣方程性態的影響,對于低掠角入射時(入射角θi>85°)的電大尺度粗糙海面電磁散射仿真時發現串行FMM是無法使用的. 而文中所提的算法CBFM對于電大尺度問題可以通過離散子域的選擇控制實際LU分解的矩陣維數,從而保證了單機操作的可行性.

接下來,為進一步說明CBFM的有效性,本文將從SCBFs的階數和離散子域的個數兩個角度展開討論,對比分別采用MoM和CBFM兩種方法的直接求解逆矩陣的維數、百分比誤差和CPU時間,同時,探討大角度入射下CBFM的有效性．以下數值計算中,圖1中粗糙海面模型的參數選擇如下:海面是PM譜海面,風速U=5 m/s,入射角θi=30°(大角度入射除外),模擬海面長度L=81.92 m,采樣間隔Δx=0.1λ,入射波頻率選擇f=1.5 GHz,即可得采用傳統MoM時的未知量個數N=4 096,直接逆矩陣求解的維數是4 096×4 096. 采用MoM計算時,在H極化方式下所用的CPU時間為15.813 s,在V極化方式下所用的CPU時間為15.406 s.

3.2 不同SCBFs的階數

將整個粗糙海面均分成4個子域,即每個子域的剖分點數是Ni=1 024,則采用CBFM時矩陣求解的維數是1 024×1 024. SCBFs分別取為2階、3階、4階、5階,表2給出了不同極化方式下,SCBFs取不同階數時,分別采用CBFM與MoM時的計算時間和百分比誤差對比. 從表中可以很明顯地看出當SCBFs的階數越高時,CBFM的百分比誤差越小,即是說SCBFs的階數越高時,CBFM與傳統MoM的計算結果吻合得越好,這是因為階數越高時各離散子域之間的互作用被考慮的越充分. 然而從表2中還可看出,階數越高時,計算時間越長. 綜合考慮計算時間和百分比誤差,作者認為當SCBFs取為4階時,仿真結果和仿真效率是最好的.

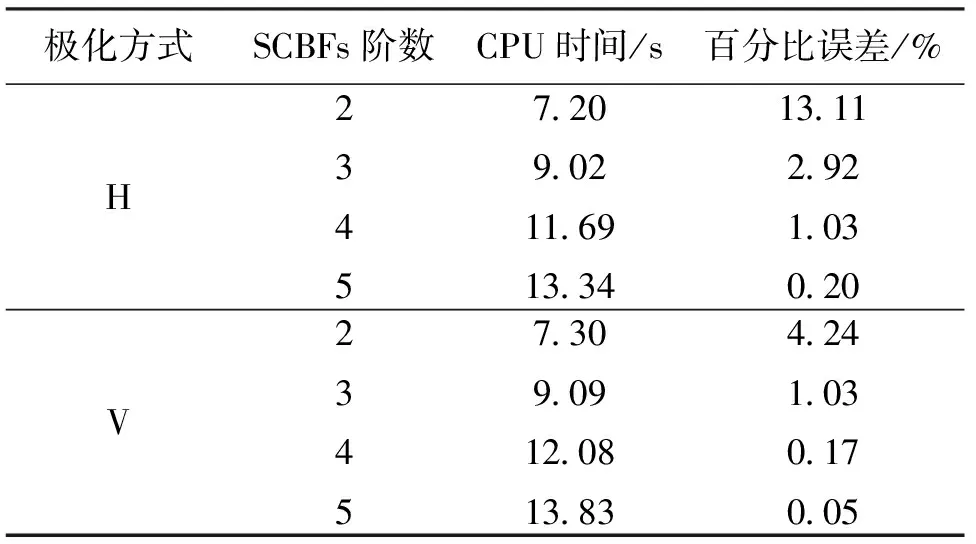
表2 SCBFs取不同階數時的CPU時間與百分比誤差Tab.2 The CPU time and the percentage error of SCBFs with different orders of SCBFs

3.3 不同離散子域個數

表3中列出了將整個粗糙海面分成不同個數離散子域時,對應的CPU時間及百分比誤差的比較.從表3中可以看出,當SCBFs的階數固定,離散子域不同時,劃分的子域越多,百分比誤差越大,這是因為SCBFs計算時忽略了相鄰子域之間的相對較強的互作用. 同時從表中可以看出,劃分的子域越多,相應的計算時間會少點,這是因為劃分子域越多時,各離散子域自作用矩陣的逆矩陣求解的維數越小,LU技術求解時間會減小,但同時SCBFs的互作用項疊加時間增長. 對比表3中的數據可以發現,離散64個子域和離散32個子域在CPU時間上的減少有限,但百分比誤差卻大大增加了,因此綜合考慮計算時間和百分比誤差,作者認為該算例中粗糙海面劃分為8個子域時,仿真結果和仿真效率是最理想的.

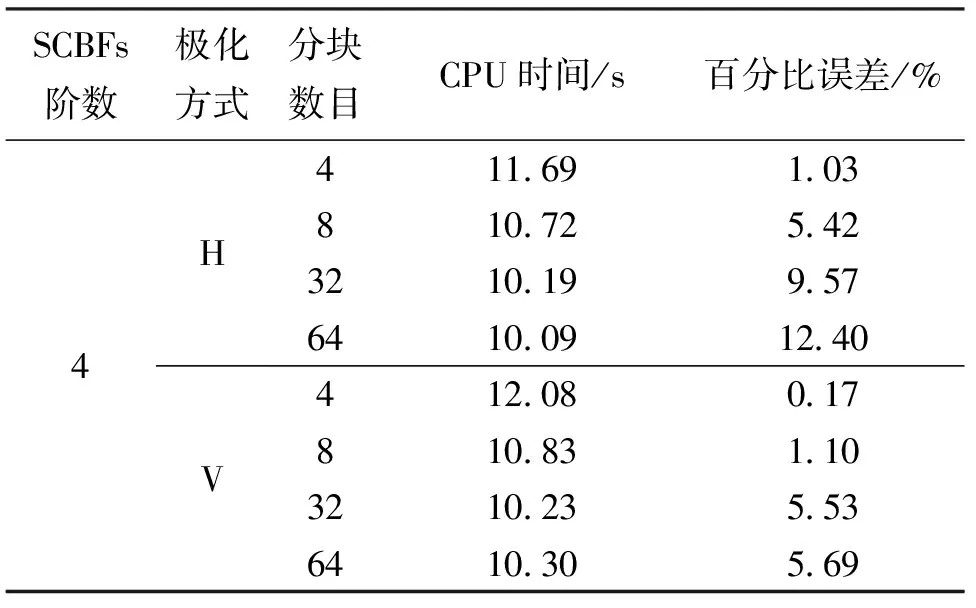
表3 粗糙海面劃分不同子域時的CPU時間與百分比誤差Tab.3 The CPU time and percentage error with different cells

3.4 大角度入射下的有效性分析

從前面的討論中可以得出,將粗糙海面分成8個子域,SCBFs取4階時,仿真結果和仿真效率較好. 現在取入射角θi=80°,其他計算條件保持不變情況下,獲得的不同極化方式下的散射系數如圖3所示,所得的表面未知量如圖4所示. 表4給出了不同極化方式下,CBFM所用的CPU時間及百分比誤差的對比. 從圖中可以看出CBFM獲得的散射系數和表面未知量與MoM的仿真結果吻合得比較好,但從表4中可以看出此時的百分比誤差卻不是很理想的,尤其是HH極化情況下的百分比誤差. 在接下來的研究中,我們將繼續分析大角度入射情況下SCBFs的階數和離散子域的個數對計算精度和計算效率的影響.

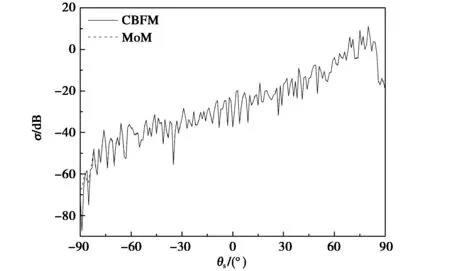
(a) H極化(a) H polarization

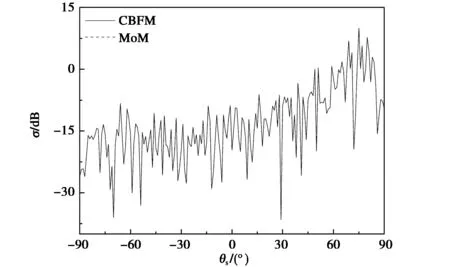
(b) V極化(b) V polarization圖3 大角度入射下采用H和V極化方式時CBFM與MoM的散射系數對比Fig.3 The scattering coefficient obtained by the CBFM and the MoM under the larger angle of incidence under H and V polarization

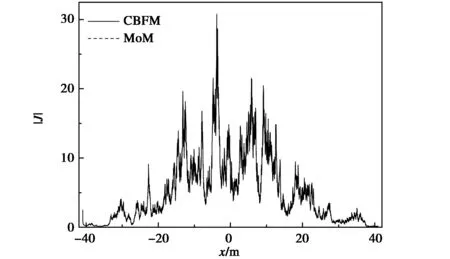
(a) H極化(a) H polarization

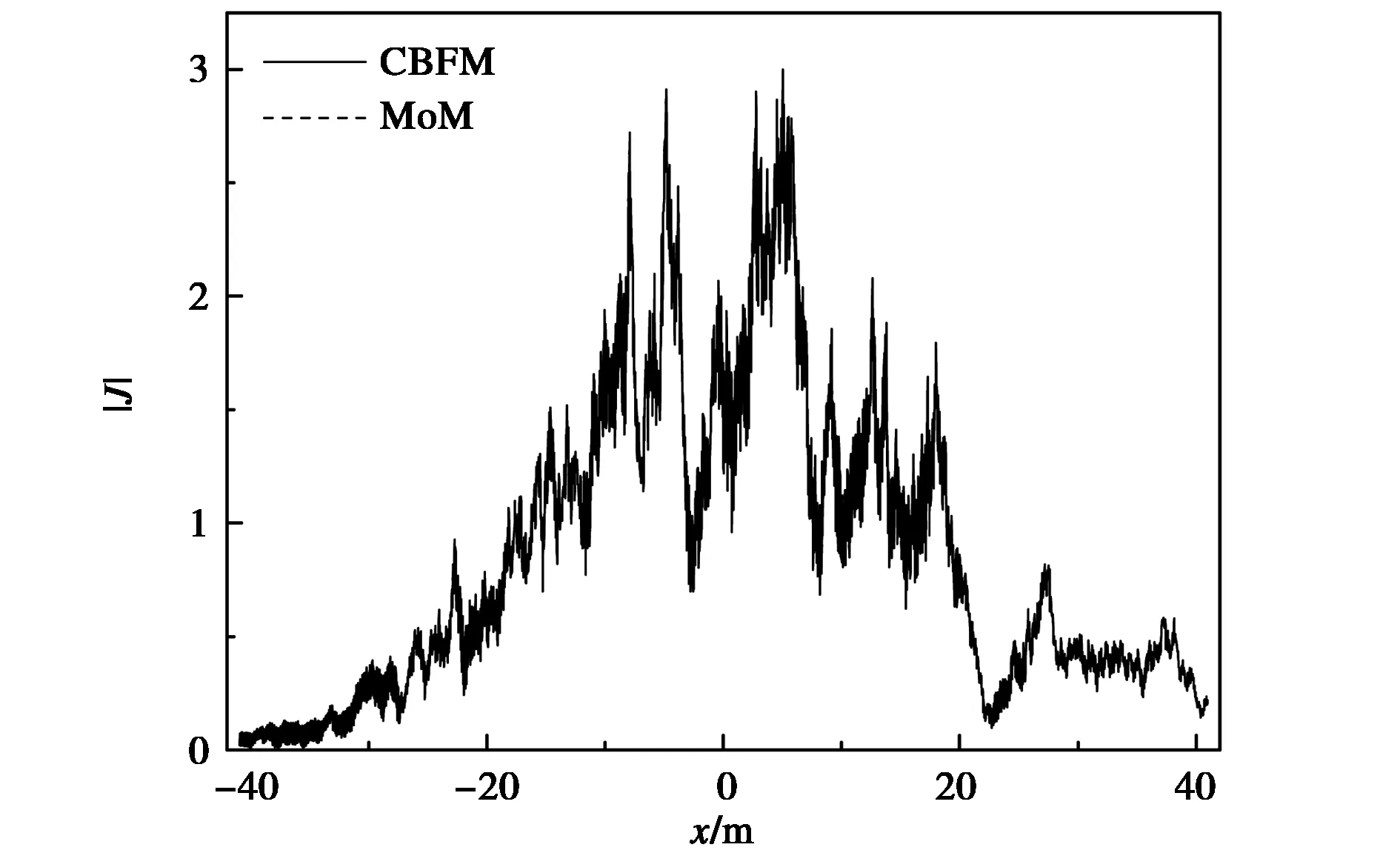
(b) V極化(b) V polarization圖4 大角度入射下采用H和V極化方式時CBFM與MoM的表面未知量的對比Fig.4 The surface unknowns obtained by the CBFM and the MoM under the larger angle of incidence with H and V polarization

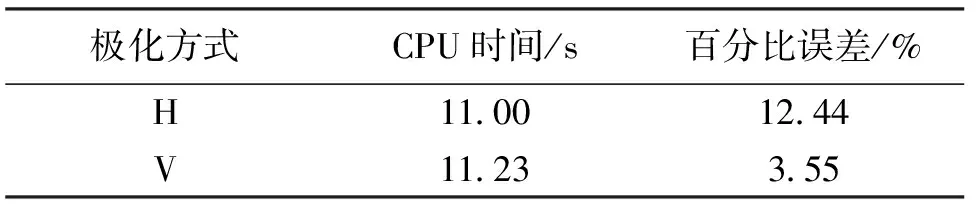
表4 CBFM所用的CPU時間與百分比誤差Tab.4 The CPU time and percentage error

4 結果與討論

本文引入CBFM快速分析了一維理想導體粗糙海面的電磁散射特性,并在兩種極化方式下與傳統MoM的計算結果進行了對比,討論了SCBFs的階數和離散子域的個數對計算精度和計算效率的影響. 當在相同離散子域的情況下,SCBFs的階數越高時,CBFM的百分比誤差越小,然計算時間越長. 當取同一階數時,劃分的子域越多,百分比誤差越高,而且計算時間減少到一定程度后就不是很明顯地減少了. 同時,在仿真結果的對比中可以發現H極化的百分比誤差比V極化的百分比誤差大,這是因為兩種極化方式的積分方程不同,相鄰離散子域的相互作用對整體散射特性的影響不同．另外,在大角度入射時,可以發現散射系數和表面未知量與MoM仿真結果吻合得比較好,但百分比誤差卻不是很理想. 在接下來的研究中,我們將繼續討論入射角度、極化方式、SCBFs的階數和離散子域的個數對計算精度和計算時間的影響,以期獲得一個經驗結論用于階數的選擇和離散子域個數的選取.