基于鏈路選擇學習算法的無設備目標定位
金杰 柯煒,2 陸俊 王彥力 唐萬春,2
(1.南京師范大學物理科學與技術學院,南京 210023;
2. 江蘇省地理信息資源開發與利用協同創新中心,南京 210023)
引 言
無設備目標定位(device-free localization, DFL)一般是通過在待檢測區域周圍設置若干無線收發節點來實現.無線節點間能夠相互通信,在空間內形成許多無線鏈路,當一個目標進入該區域,便會衰減一部分鏈路,相應的這一部分鏈路的接收信號強度(received signal strength,RSS)值也會發生變化.因此,可以通過RSS值的變化來獲得目標的位置信息.文獻[2-3]中將DFL問題建模成一個機器學習問題并通過指紋匹配的方法將其成功解決,它通過當前鏈路測量值與訓練數據庫進行比較來估計目標位置.受計算層析成像算法的啟發,文獻[4-7]中將DFL問題轉換成無線電層析成像問題,并使用正則化的方法進行求解.隨后,Wang J等人將DFL推廣到多維測量條件[8],并通過改進陰影衰減模型進一步提高了DFL的定位精度[9-11].常儷瓊等人針對環境噪聲對鏈路接收信號的影響提出了一種能夠有效消除環境噪聲的DFL方法[12];劉凱等人也就射頻層析成像(radio tomographic imaging, RTI)方法的實時性問題提出了自己的改進方法[13].
隨著壓縮感知(compressive sensing,CS)[14-15]的迅速發展,根據目標的空間稀疏性,文獻[16]將DFL成功建模成一個稀疏信號重建問題并提出了一種貪婪匹配追蹤(greedy matching pursuit, GMP)算法來解決.GMP算法通過排查部署區域里所有位置來確定目標,但是如果部署區域太大,其計算復雜度也會大大提高,并不適用于實時定位.在GMP的基礎上,文獻[17]提出了貝葉斯貪婪匹配追蹤(Bayesian greedy matching pursuit, BGMP)算法,充分利用先驗條件加速了算法并過濾了部分誤差位置,在運算速度和定位精度上都有了一定提高.
上述這些方法雖都成功地將CS應用到DFL,但由于CS模型中所采用的權重字典都是基于經驗模型構建,與實際情況往往存在偏差,所以定位性能達不到預期的效果.針對權重字典的模型誤差,文獻[18-19]都提出了采用字典學習的算法來糾正原權重字典的模型誤差.
此外,在DFL求解目標位置時,傳統做法是將無線傳感網中的所有鏈路的變化情況都考慮進計算,然而實際情況是目標僅會遮擋、衰減一部分的鏈路.如果計算所有鏈路的變化情況不僅會導致冗余的計算步驟,影響DFL系統的實時性,而且也會因為計算誤差的累積和“無關”鏈路的擾動誤差導致定位誤差.
本文針對上述兩方面問題,提出了一種基于鏈路選擇學習(link selection learning,LSL)的DFL算法.不同于文獻[18-19]中的字典學習方法,該算法在更新字典的過程中,不僅糾正了原權重字典的模型誤差,而且結合位置的物理空間信息,完成了有效鏈路選取,實現了對字典維數的壓縮以及對野值目標位置的過濾.
1 系統模型及問題描述
本節,我們首先介紹將RSS測量值與目標空間位置關聯起來的CS系統模型,再討論字典不匹配以及鏈路選取問題.
1.1 系統模型
假設定位區域周圍布置了L個無線節點,并且將定位區域劃分為N個網格,可以形象地將這些網格稱為“像素”.假設區域中有K個待檢測目標,如果網格足夠密集,那么每一個目標都可以保證有一個像素點與它對應.如果K?N,離散空間域中的目標位置可以精確地表示為稀疏向量x.如果目標位于定位區域的相應位置,向量x中對應位置的元素則有非零值,而向量x中其他元素等于零.如上所述,可將DFL轉換為在稀疏向量x中確定非零元素及其特定位置的問題.則稀疏定位模型可以表示為
y=Dx+n.
(1)
式中:y是RSS測量值向量;D為權重字典;n為測量噪聲.傳統的做法是通過經驗模型構建固定的權重字典D,再通過CS重構算法求解稀疏向量x,從而得到目標的位置信息.
1.2 問題描述
對于DFL問題中的權重字典,傳統做法都采用一個固定的模型來描述.最常用的為橢圓模型[4],該模型假設目標只對鏈路所在直線為直徑的橢圓區域產生影響,當像素中心到兩個節點的距離的和大于橢圓直徑加上短軸長度時,判斷該像素有權值.根據該方法,權重字典中的元素Dij可表示為

(2)
式中:dij為節點i到節點j的距離;di、dj分別為像素中心到節點i和節點j的距離;ρ為橢圓的短軸長.該模型假設權重值與鏈路的長度成反比,缺乏理論依據,并且一個橢圓內所有格點對應的權重相同也不符合實際.因此,基于橢圓模型構造的字典D與實際字典D0之間不可避免地存在誤差.為清楚起見,用一個誤差字典矩陣Γ來描述數學解析字典與理想字典之間的差異,則CS框架下的稀疏定位模型可以表述為
y=Dx+n=(D0+Γ)x+n.
(3)
值得注意的是,誤差矩陣Γ不僅是未知的,而且隨著時間和環境的變化而變化.由于模型字典D與理想字典D0之間存在不匹配,所以在稀疏恢復過程中出現誤差是不可避免的.為了獲得準確的定位結果,本文算法采用自學習的方式來訓練字典,減輕模型誤差.
在解決DFL問題時,如何選擇受到目標影響的有效鏈路也是影響定位結果的一個重要因素.傳統的做法是考慮無線傳感網(wireless sensor network, WSN)中所有鏈路的變化情況,如參考文獻[4-7],或者為了滿足CS扁矩陣的要求,隨機選取一定的鏈路數參與計算[16].考慮所有鏈路的變化情況,不僅會導致冗余的計算步驟,影響DFL系統的實時性,而且也會因為計算誤差的累積和“無關”鏈路的擾動誤差導致定位誤差.而隨機選取一定的鏈路參與計算,則會因為有時鏈路選擇的不準確性,導致較大的定位誤差.為了規避兩種鏈路處理方法的弊端,本文算法根據移動目標的位置相關性,在字典更新的同時,完成對參與計算鏈路的選取,不僅壓縮了字典維度,加速了算法,而且也濾除了部分野值目標位置.
2 LSL算法
本節詳細介紹LSL算法,算法包括兩個階段:訓練階段和定位階段,如圖1所示.在訓練階段中我們同時完成字典更新以及鏈路選擇,得到降維后的匹配字典;在定位階段,使用修正后的匹配字典作為權重矩陣,進行稀疏重構.
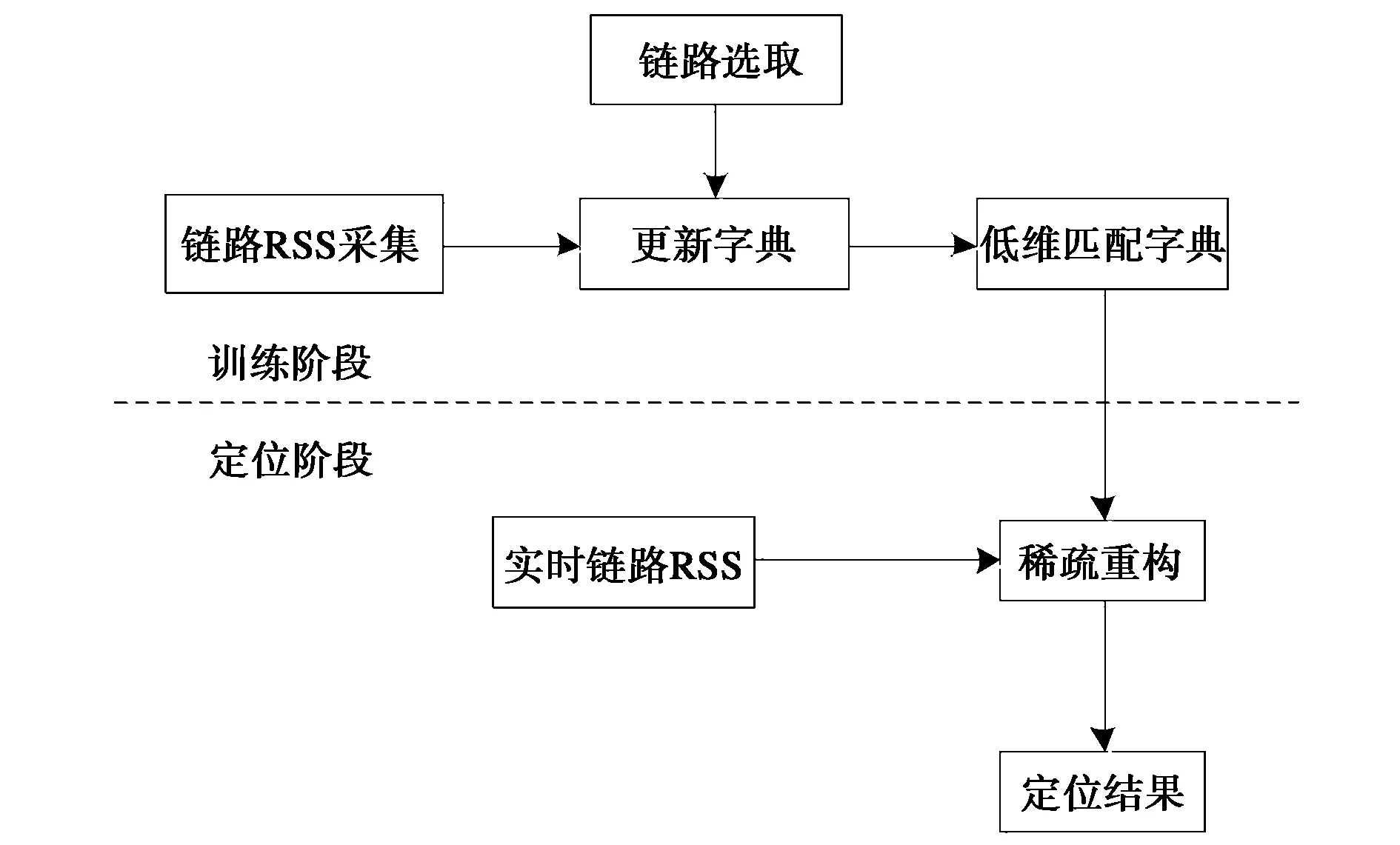
圖1 LSL算法流程圖Fig.1 Flowchart of LSL algorithm
2.1 訓練階段
2.1.1 字典學習
1996年,Olshausen發表了著名的Sparsenet字典學習算法[20],該算法奠定了字典學習理論的基礎,隨后許多改進的字典學習算法也相繼出現了.Lee等提高了Olshausen字典學習算法的速度[21];受廣義聚類算法的啟發,Engan等對Olshausen的Sparsenet字典學習算法進行了改進,提出了最優方向(method of optimal directions, MOD)字典學習算法[22];為減小MOD算法的復雜度,Aharon等又提出了逐列更新字典的KSVD算法[23].本文借鑒上述字典學習的思路,對模型字典進行更新.
由于有L個無線節點,一共可以組成M=(L-1)L/2條無線鏈路,這意味著一次測量可以得到M維的測量矢量yi=[y1,y2,…,yM]T.考慮到訓練要求,我們一共采集P個這樣的測量矢量,組成訓練矩陣Y;其對應的稀疏矢量xi(i=1,2,…,P)組成稀疏矩陣X.根據字典學習理論,要尋找權重字典的最優表示D,我們僅需求解

(4)
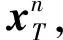


(5)
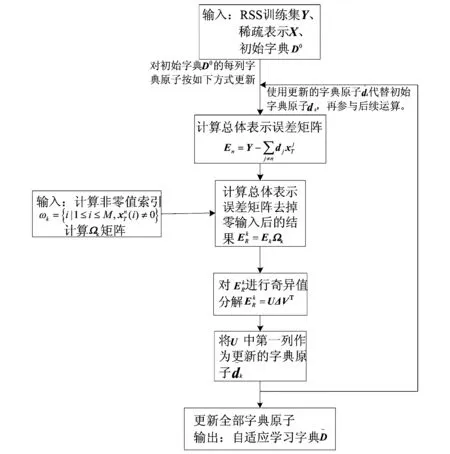
圖2 LSL算法字典學習階段流程Fig.2 Dictionary learning stage process of LSL algorithm
式(5)中,DX被分解為N個秩為1的矩陣的和,假設其中N-1項都是固定的,剩下的第n列就是需要處理更新的.矩陣En表示去掉原子dn的成分在所有N個樣本中造成的誤差,稱為誤差矩陣,如下所示:

(6)
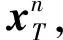

(7)


(8)

2.1.2 鏈路選取
為了加速字典學習過程,同時消除野值鏈路的影響,提出一種鏈路選取方法.根據移動目標的時空相關性,可以依據目標上一時刻位置來判定下一時刻目標可能出現的區域,僅選取通過該先驗區域中的鏈路參與計算.
假設目標初始位置位于像素j處,下一時刻目標可能出現的位置一定是在以像素j為圓心,半徑為h的圓內.半徑h設置如下:
h=Vmax×tint.
(9)
式中:Vmax為定位目標的最大速度;tint為兩次定位算法運行的時間間隔.由于目標只可能出現在先驗區域內,因此只有經過先驗區域的鏈路才可能真正被目標所影響.為了判斷鏈路是否經過置信區域,可以將鏈路看作一條直線,于是上述問題便轉化為直線是否經過圓的數學問題.如圖3中節點6到節點19的鏈路所示,要判斷該條鏈路是否經過置信區域,只需判斷圓心到直線的距離H是否小于圓的半徑h.由于在DFL問題中,像素點到無線節點的距離及無線節點間的距離都是容易獲得的,因此對于這個問題我們可以根據海倫公式和三角形面積公式很方便地求得H,即
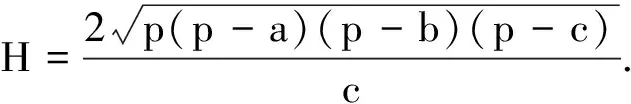
(10)
式中:a、b、c為三角形的三邊長;p為三角形的半周長;H為三角形c邊上的高.凡是滿足H 但對于邊界鏈路,這種判定方法會產生誤判,如圖3中節點4到節點5的鏈路所示.從圖上直觀地看到,從先驗區域圓心處到無線節點4、5之間鏈路所在直線的垂直距離明顯小于先驗區域半徑,但節點4到節點5這條鏈路卻不經過先驗區域.不過,由于DFL通常只考慮邊界內的目標定位,目標出現在邊界上的特殊情況實際中一般不會出現,因此邊界鏈路可以直接排除,所以并不影響上述鏈路選取方法. 圖3 鏈路選取Fig.3 Link selection 在完成訓練階段后,我們得到一個更新后的匹配字典;稀疏恢復階段,我們用該字典替代原始權重字典,并從鏈路索引表index中挑選對應的RSS變化值,最后使用CS稀疏重構算法求解目標位置.文獻[16]中提出了一種BGMP算法得到了較好的定位效果,因此本文也延用了這種方法. 為了體現本文提出算法的性能,本文分別在室外和室內環境下進行實驗驗證.為了便于與文獻[17]的結果進行比較,其中室外實驗數據采用猶他州大學SPAN實驗室提供的數據;室內實驗數據則由本實驗室搭建的DFL系統測量得到.實驗中,我們先采集目標在各個位置處的RSS值作為訓練數據,根據本文所提的鏈路選擇學習方法,自適應學習得到匹配字典;再使用匹配字典以及實時采集的RSS數據,求解目標位置.另外,參考文獻[24]的做法,不失一般性,我們假設目標的初始位置是已知的,首先保證了起點不會出現偏差,但為了保證統計結果的有效性,起點位置坐標不參與統計. 3.1.1 實驗設置 室外實驗直接采用SPAN實驗室提供的數據進行[數據來源:http://span.ece.utah.edu/rti-data-set].該實驗的定位區域大小為6.3 m×6.3 m,在定位區域邊緣以0.9 m的間隔共部署了28個無線節點,為了與文獻[17]中的方法進行比較,本文也將區域劃分為49個小網格,數據集給出了目標位于其中35個參考位置的RSS值,即P=35,并且數據集中也給出了采集這35個參考位置數據時目標的移動軌跡,如圖4所示(我們可以根據移動軌跡來進行鏈路選取).其他參數設置如下:初始字典采用橢圓模型構造,鏈路選擇區域閾值設置為h=1.5 m. 圖4 室外實驗目標移動軌跡圖Fig.4 Target track map of the outdoor experiment 我們將所提LSL算法與文獻[17]中所提算法進行比較,將文獻[17]所提算法記為算法A,為了比較不同算法間的重構性能差異,還與最小化l1范數算法進行了比較,將其記為算法B.我們采用真實位置和估計位置之間的均方誤差作為評估算法定位精度的標準. 3.1.2 實驗結果分析 為了直觀反映定位效果,本節先給出目標在一個位置的定位結果對比圖,然后給出統計分析結果. 圖5為當目標位于(0.9,2.7)m位置時,三種算法的定位結果比較.可以看到:算法B效果并不理想,不僅目標估計位置與真實位置間相差較大,并且會伴隨有偽目標的情況;而算法A對于某些位置的目標定位結果會出現一至兩個格點的偏差,如圖5(a)所示;而本文算法能夠實現準確的定位. (a) 真實位置(單位:m) (b) 算法A定位結果 (a) Real location(m) (b) Location result of algorithm A (c) 算法B最小化定位結果 (d) LSL定位結果 (c) Minimized location result of algorithm B (d) Location result of LSL 圖5 室外環境三種算法定位結果對比Fig.5 Comparison of positioning results of three algorithms in the outdoor environment 圖6給出了在單目標情況下,本文算法和算法A、算法B的定位誤差累積概率分布圖.由于劃分的像素點的尺寸為0.9 m,并且當目標位于某個像素點時,都默認為該目標在這個像素點的中心位置,因此,定位誤差的累積分布函數圖會呈現折線的形狀.從圖中可以看到,由于LSL與算法A最大定位誤差較小,所以累積分布函數圖呈現一種陡峭的上升趨勢.而LSL相比于算法A其優勢體現在,由于學習字典不僅糾正了傳統權重矩陣的模型誤差并且也過濾部分誤差位置,從而使得絕大部分點都能夠準確定位.定位誤差的詳細統計結果如表1所示,我們可以看到,本文所提的LSL算法在室外環境下,定位平均誤差以及均方根誤差上都有米級以上的提升. 圖6 室外環境三種算法定位誤差的累積分布函數Fig.6 CDF of three algorithms in the outdoor environment 表1 室外環境定位誤差對比Tab.1 Comparison of positioning error in the outdoor environment 3.2.1 實驗設置 室內實驗在南京師范大學行健樓一樓大廳進行,實測環境布局如圖7所示,該定位環境三面為磚墻,一面為全玻璃墻面.實測數據采用的是TI CC2530無線節點,采用IEEE802.15.4協議和2.4 GHz頻率.此實驗定位區域為5 m×5 m,在區域邊緣以1 m的間隔共部署了20個無線節點,我們將該定位區域以1 m為邊長劃分為25個小網格點.采集目標位于各位置時的RSS數據,并記錄目標移動軌跡,如圖8所示. 圖7 室內實驗環境Fig.7 Indoor experiment environment 圖8 室內實驗目標移動軌跡圖Fig.8 Target movement track map of indoor experiment 3.2.2 實驗結果分析 圖9為當目標位于(1,1)m位置時,三種算法的定位結果比較. (a) 真實位置(單位:m) (b) 算法A定位結果 (a) Real location(m) (b) Location result of algorithm A (c) 算法B最小化定位結果 (d) LSL定位結果 (c) Minimized location result of algorithm B (d) location result of LSL 圖9 室內環境三種算法定位結果對比Fig.9 Comparison of positioning results of three algorithms in the indoor environment 從圖9我們可以得出和室外環境一致的結論:本文所提的LSL算法,能夠有效修正原傳統權重字典的模型誤差,并且能夠過濾部分誤差位置,因此對于大部分目標位置都能夠實現較準確的定位.現給出在室內情況,目標位于各個位置,多次實驗的統計結果(其中每個位置我們都進行了110次實驗):圖10為在單目標情況下,本文算法和已有算法的定位誤差累積概率分布.本文算法,無論是能準確定位到目標點的概率,還是最大定位誤差,都優于其他算法.本文算法在定位精度上有較大幅度的提升.室內環境定位誤差的詳細統計結果,如表2所示,本文所提算法相比算法B在平均誤差上提高了1.9 m左右,相比算法A平均誤差大致提高了0.5 m;所提LSL算法的均方根誤差也相比算法B、算法A,分別提高了29.7%和14.5%. 圖10 室內環境三種算法定位誤差的累積分布函數圖Fig.10 CDF of three algorithms in the indoor environment 表2 室內環境定位誤差對比Tab.2 Comparison of positioning error in the indoor environment 綜上所述,本文所提的LSL算法無論是室外環境,還是室內環境,其定位精度都大幅優于其他算法,因此具有很好的定位性能. 圖11給出了算法B、算法A與LSL算法在室外和室內情況下的運行時間對比. 圖11 三種算法的運行時間Fig.11 Running time of three algorithms 如圖11所示,盡管本文算法增加了字典學習環節,但由于LSL算法在訓練階段完成了對鏈路的篩選,學習字典的維度大大下降,使得在稀疏重構階段,計算量大大減少,因此算法運行速度較其他算法非但沒有下降,相反還有較大的提升. 本文針對CS框架下DFL的傳統模型權重字典存在字典不匹配問題,提出了一種鏈路選擇學習算法(LSL),能夠在字典更新過程中進行鏈路選取,同時解決了字典不匹配以及有效鏈路選擇的問題.經室外及室內實驗驗證,這種算法不僅很好地解決了傳統方法的字典不匹配問題,而且能夠過濾部分誤差位置,在定位精度和算法運行時間上都有優異的表現.下一步將考慮該方法誤差的克勞美·羅界,并將該方法推廣到多目標DFL定位.
2.2 稀疏恢復階段
3 實驗驗證
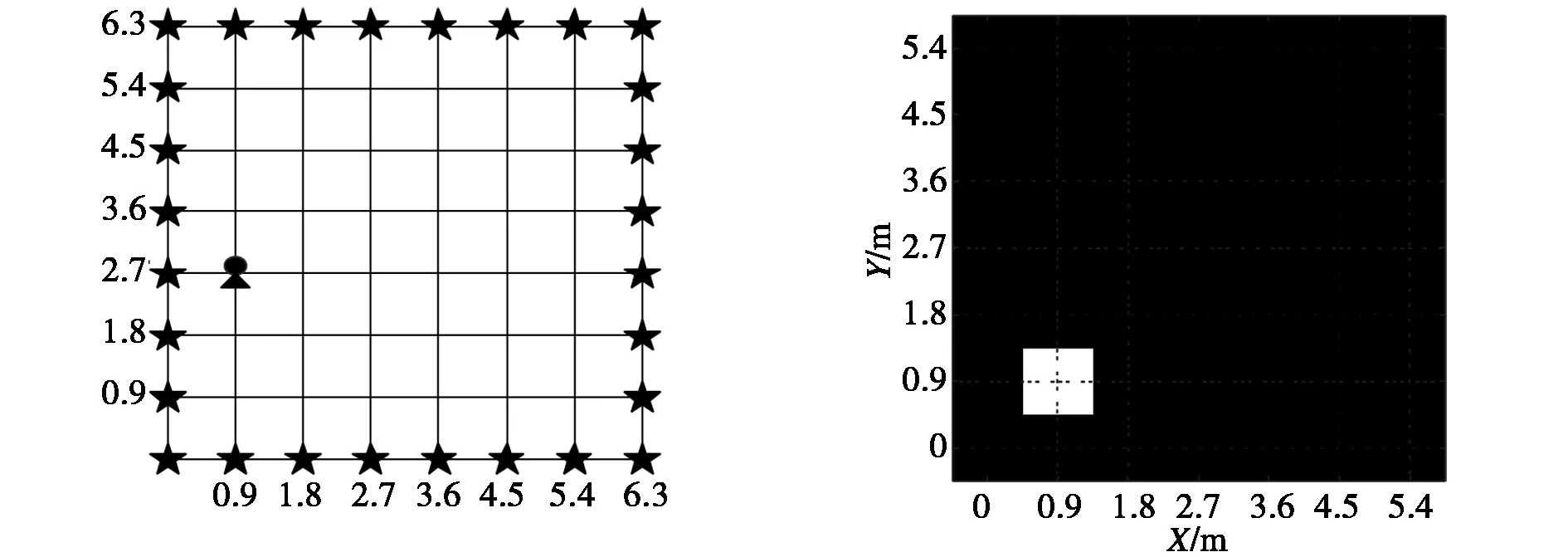
3.1 室外情況




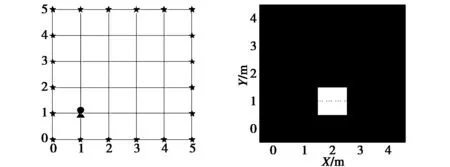
3.2 室內情況





3.3 算法運行時間分析

4 結 論

