基于自組織聚類的多敏感屬性數據發布算法

， ,

(1.北京電子科技學院 研究生部， 北京 100070； 2.西安電子科技大學 計算機學院， 陜西 西安 710071)

隨著數據挖掘技術的飛速發展以及數據擁有者對隱私數據泄露問題的高度關注，隱私數據發布技術不斷進步。如何保證隱私數據在發布后敏感信息不易被攻擊，同時數據可挖掘性能夠得到極大保證，針對這一問題，國內外學者給出了多種可行方案。

l-匿名模型[1]、l-多樣性模型[2]和l-closeness模型[3]是比較經典的3種隱私保護模型。基于這些模型，許多算法被相繼提出[4-10]。這些算法在處理單敏感數據發布時雖然有可觀的抗攻擊性，但是不適用于多敏感數據發布。針對多敏感屬性數據發布隱私保護，楊曉春等[11]提出了基于有損鏈接的多維分桶技術，其將每一敏感值映射到對應分桶，按照策略分組，實現組內滿足l-多樣性。其他基于有損鏈接很多算法被提出[10-12]，但有損鏈接會破壞非敏感屬性與敏感屬性間的關聯關系，影響到發布后數據的信息可挖掘性。與有損鏈接的方法對比，無損鏈接的方法較好地保存了敏感數據與非敏感數據關聯性。基于無損鏈接的算法較少，文獻[13]中提出了基于l-多樣性模型的無損鏈接發布算法,但不適用于敏感屬性值多樣性差異過大的情況。為了解決該問題，本文中提出了(l,x,w)多樣性模型，該模型通過約束等價組內敏感屬性多樣性及均勻性來實現匿名保護，并基于該模型提出了多敏感屬性數據發布的基于信息熵的l-多樣性聚類(entropy basedl-diversity clustering, EBLC)匿名算法。該算法按照非敏感屬性對數據進行聚類后，在同簇中按照策略生成滿足多樣性的等價組，對等價組內元組泛化后進行發布。對該算法進行仿真實驗，通過運行效率、信息損失等實驗結果驗證算法的匿名效果。

1 基本概念

對于一般待發布數據，針對其屬性可劃分為個人標識屬性(individually identifying attribute, IIA)、準標識符屬性(quasi-identifier attribute, QIA)以及敏感屬性(sensitive attribute, SA)。IIA用于直接識別個人身份信息，QIA可結合外部數據識別個人信息，SA包含個體隱私信息。

設T={Q1,Q2, …,Qp,S1,S2, …,Sd}(p為分類性屬性個數，d為數值性屬性個數)為待發布數據集，其中Qi(1≤i≤p)表示準標識符屬性，|Qi|表示敏感屬性Qi在T中不同值的個數。Sj(1≤j≤d)表示敏感屬性， |Sj|表示敏感屬性Sj在T中不同值的個數。T中有n個元組ti(1≤i≤n)，T的元組數目用|T|=n表示，對任意元組ti∈T，用ti、X表示元組ti在屬性X上的取值。

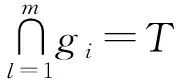
文獻[10]中提出了基于有損鏈接的(l1,l2, …,lm)模型，文獻[13]中提出了(l,m)多樣性模型。在文獻[10]中，(l1,l2, …,lm)模型與噪聲添加配合使用才能抵抗概率攻擊，但是引入的噪聲污染了數據，而文獻[13]中(l,m)模型不適用于敏感屬性值個數差異過大情況，特別是，當某一個敏感屬性取值為2時，此時l的選取受到該敏感屬性候選值個數限制。本文中提出(l,x)多樣性模型用以解決此類問題。

定義2((l,x)多樣性)gi為T的一個等價組，對于任意敏感屬性Sj，多樣性變量x為

x=min{l, |Sj|}

。

(1)

若等價組gi在敏感屬性Sj上的不同取值數不小于x， 則稱等價組gi滿足(l,x)多樣性； 若對任意gi∈T，gi均滿足(l,x)多樣性， 則稱T滿足(l,x)多樣性。

敏感屬性信息如表1所示。當l=3時，顯然年收入的屬性個數已經無法滿足l-多樣性。

表1 敏感屬性信息

盡管也可以使用(l1,l2, …,lm)模型進行數據匿名發布，但是該模型需要引入噪聲，這會污染數據。若使用(l,m)模型則需要調整使l=2，這樣使得發布后數據的安全性降低，無論使用以上哪種模型都不合適；而當使用(l,x)多樣性模型在生成等價組時，只需要使敏感值多樣性小于l的敏感屬性滿足x多樣性即可。表2所示為一個l=3時的滿足(l,x)多樣性的等價組。

2 算法介紹

2.1 聚類生成

近些年來，基于聚類的敏感數據發布算法不斷發展[7,9-10,14-17]，但大多是基于有損鏈接或者單敏感屬性。其中文獻[18]中提出的(t, sim, dif)算法在抗概率攻擊以及同質攻擊方面均有良好表現；但是，由于該算法是從敏感屬性部分生成聚類構造等價組，同時，該算法為單敏感屬性數據發布算法，因此無法解決多敏感數據發布問題。基于文獻[18]中通過聚類尋找等價組思路，本文中提出了針對多敏感屬性數據發布的EBLC算法，由非敏感屬性生成聚類構造等價組，通過對原數據進行去噪點以及聚類劃分，在聚類基礎上生成滿足目標約束的等價組，保證生成等價組有全局最優信息損失與抗攻擊性。

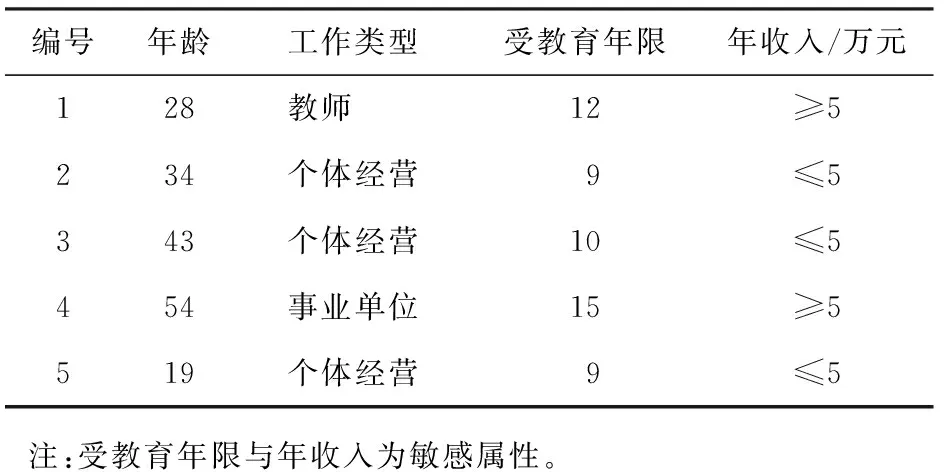
表2 多樣性為3時滿足(l, x)多樣性的等價組

2.1.1 距離定義

本文中主要針對分類型數據及數值型數據進行研究， 根據不同類型數據， 定義不同的距離度量公式。

定義3(非數值型屬性距離) 設屬性X為分類型屬性，按照不同取值構建屬性值分層樹，設xi表示該屬性的某一取值，則距離函數為

Dclassi(xi,xj)=|1/flevel(xi,xj)-1/flevel(xi)|+

|1/flevel(xi,xj)-1/flevel(xj)| ，

(2)

式中：flevel(xi)表示分類值xi在分層樹中的層級；flevel(xi,xj)表示值xi、xj在分層樹中最小祖先節點的層級；Dclassi(xi,xj)表示屬性值xi與xj的分類距離。

定義4(數值型屬性距離) 設屬性X為數值型屬性，xi為該屬性的某一取值，則距離函數為

Ddigit(xi,xj)=|xi-xj|/(max{X}-min{X})，

(3)

式中：Ddigit(xi,xj)表示數值屬性值xi與xj的距離；max{X}表示屬性X最大值；min{X}表示屬性X的最小值。

定義5(元組距離) 元組ti、tj(i≠j)為表T的2個元組，則元組間距離函數為

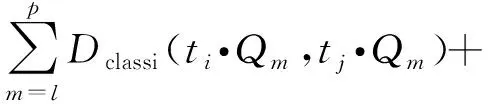
(4)

2.1.2 聚類的生成算法

使用k均值的方法進行聚類，考慮到傳統k均值方法的k值以及初始點的設定對聚類結果的影響，本文中使用自組織k均值算法(self-organizingk-means algorithm, SOKM) 。

算法1：自組織k均值算法。

輸入：元數據集表T、 停止條件δ。

輸出：數據集聚類信息表T′。

1) 令聚類數目Cnum=1，T′記錄T的簇劃分以及簇中心距離信息，令可移動元組數目Cmove=|T|，對原數據集T使用二分k均值算法進行二分;

2) 遍歷當前所有分簇，對每一個分簇進行二分聚類，對比其他簇中元組與其原簇質心距離與新生簇質心的距離，將該元組劃入距離近的一簇，統計每一次二分后移動的元組數目，選擇移動數目多的簇進行二分；

3) 令Cmove等于元組最大移動數目，令Cnum+1，并更新T′；

4) 檢查Cmove與δ，當Cmove小于δ時停止分裂，輸出T′，否則重復步驟2)和3)直到滿足停止條件。

考慮到離群點對匿名算法的影響，在聚類部分對離群點進行處理，計算所有簇的半徑，依據半徑設定離群點判定閾值，當超出該閾值則判定為離群點，劃入簇0中。

2.2 算法核心介紹

2.2.1 (l,x,w)多樣性

信息熵常被用來描述信源的不確定度。為了提升發布數據抗同質攻擊以及概率攻擊的能力，在生成等價組時使用信息熵作為策略之一。

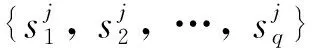
(5)

定義7(敏感標準熵) 設gi為一滿足(l,x)多樣性的等價組， 對于任意敏感屬性Sj， 其標準熵函數為

(6)

當等價組gi中敏感屬性Sj的多樣性數目為x時，可知其敏感標準熵為其信息熵的最大值，此時該屬性的不確定度最大。

定義8((l,x,w)多樣性) 設gi為一滿足(l,x)多樣性的等價組， 對于任意敏感屬性Sj，若等價組中該敏感屬性敏感信息熵與敏感標準熵之比不小于w，則稱等價組gi滿足(l,x,w)多樣性，若T中所有等價組均滿足(l,x,w)多樣性，則稱T滿足(l,x,w)多樣性。

EBLC算法即對原始數據集T在聚類劃分得到T′后， 分簇尋找滿足(l,x,w)多樣性的等價組， 最后對同一等價組按分組中心泛化， 最終得到發布數據集T*。 對于泛化后產生的信息損失， 給出以下定義。

定義9(等價組信息損失) 設gi為一滿足(l,x,w)多樣性的等價組，t為等價組中的元組，t′為等價組組中心，定義等價組泛化信息損失函數為

(7)

定義10(全局信息損失) 設T*為數據集處理后得到的滿足(l,x,w)多樣性的待發布數據集，其等價組集合G={g1,g2, …,gs}，全局信息損失函數為

(8)

定義11(平均信息損失)T*為數據集T處理后得到的滿足(l,x,w)多樣性的待發布數據集，Iinfoloss(T*)為全局信息損失，則平均信息損失函數為

ηinfoloss(T*)=Iinfoloss(T*)/|T*|

，

(9)

式中|T*|為數據集T*的元組數目。

2.2.2 基于信息熵的多樣性聚類匿名算法

算法2：EBLC算法。

輸入：元數據集T、 聚類信息T′、 多樣性l、 敏感熵比值w。

輸出：可發布數據表T*。

1) 獲取表T所有敏感屬性的多樣性集L={l1,l2, …,ld}；

2) 由T′得到所有的簇集合信息C={c1,c2, …,ck}，按照簇半徑進行升序排序得到半徑信息矩陣R；

3) 分別計算所有簇中心距離，并按照升序排序，得到簇間距離信息矩陣N，令T*為空，并依據T′得到所有簇的半徑升序矩陣Cradius；

4) 選擇當前簇集中半徑最小的簇作為等價組生成簇ci，令等價組gtmp為空;

5) 當ci中元組數目大于l時，按照第1次添加l條元組，第1次之后每次添加1條元組的原則向空的gtmp中添加記錄，每次添加后檢查gtmp是否滿足(l,x,w)并刪除ci中對應元組；

6) 當gtmp滿足(l,x,w)多樣性時將gtmp中元組添加到T*，并清空gtmp；

7) 重復步驟5)和6)直到ci為空并從C中刪除當前ci；

8) 此時若gtmp非空則選擇剩余簇中質心與當前ci質心最近的簇作為新的ci，若gtmp為空則對照Cradius與C選擇C中半徑最小的簇最為新的ci；

9) 重復步驟5)到8)直到C為空，得到T*，對T*中元組按照不同等價組質心對其進行泛化后發布T*。

2.3 基于信息熵的多樣性聚類匿名算法復雜度分析

本算法對數據匿名處理分為2個部分即聚類及等價組的生成。

聚類部分的每一次二分可分為記錄重劃分以及簇二分2個部分， 這2個部分每一次的時間復雜度分別為O(n-ni)和O(nit),其中ni為當前遍歷簇大小，t為二分聚類的平均迭代次數； 遍歷所有簇的時間復雜度為O[nt+n(ktmp-1)]， 其中ktmp為每一次遍歷時的分簇總數； 聚類部分的時間復雜度為O(nkt+nk2)， 其中k為最終的分簇數目。

等價組生成部分復雜度最壞情況為O(n2)，最優情況為O(n)，因此，EBLC算法復雜度最壞情況為O[n(kt+k2+n)]，最優情況為O[n(kt+k2+1)]。

2.4 基于信息熵的多樣性聚類匿名算法抗攻擊分析

由于等價組滿足(l,x,w)多樣性， 因此任意等價組內元組t， 對任意敏感屬性Si， 可以保證至少存在x-1條元組與t在屬性Si上的取值不同，保證了發布后數據的抗同質攻擊能力。

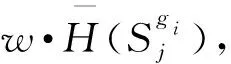
3 實驗結果與分析

3.1 實驗方案

為了驗證EBLC算法有效性，通過仿真實驗，對EBLC算法進行實現，從執行時間、信息泄露、信息損失等方面評估EBLC算法的性能，實驗結果為30次實驗的平均值。硬件環境為Intel(R) Core(TM)i3-3240CPU@3.40GHz 4.00GB RAM。實驗軟件環境為Windows10平臺、 MATLAB2016a軟件。

3.2 實驗數據

使用匿名算法研究領域通用的標準測試數據集，即UCI Machine Learning Repository中的Adult標準數據集。

實驗選取的屬性集合如表3、 4所示

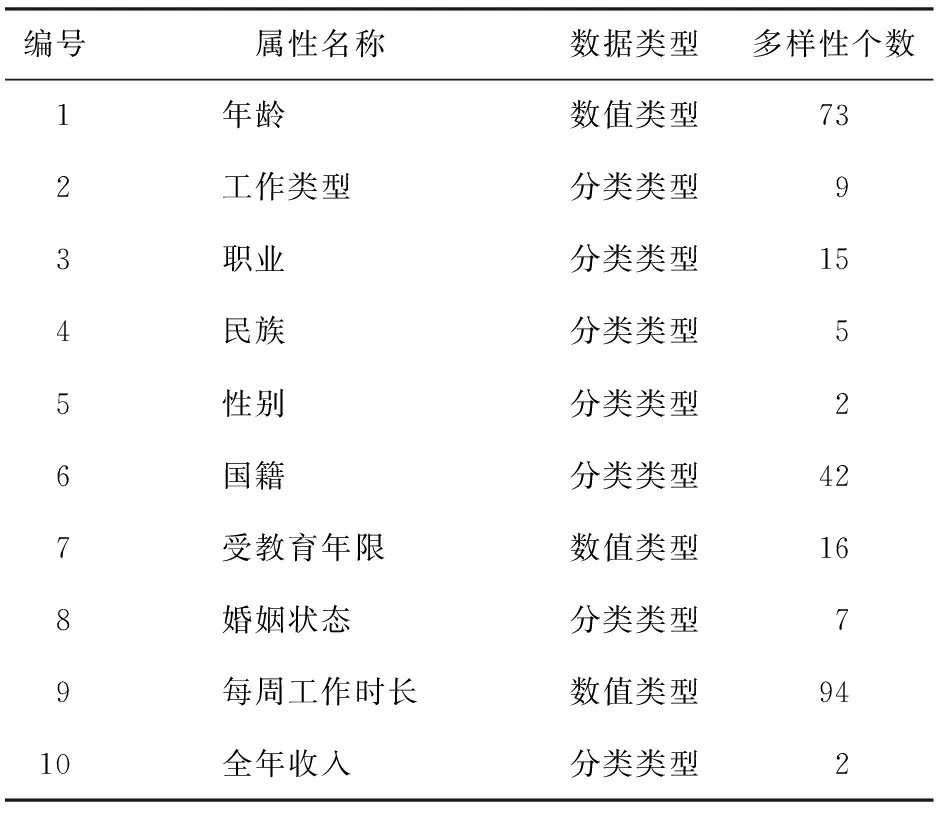
表3 實驗數據集信息

表4 敏感屬性候選信息

3.3 實驗結果

3.3.1 運行效率

圖1所示為敏感屬性m=3、多樣性l=4、信息熵比率w=0.75時，數據量級改變條件下算法的運行時間。觀察發現：隨著數據量的增加，算法的運行時間隨之增加；同時，等價組生成部分的運行時間較短，聚類部分的運行時間長，但運行時間仍然在可以接受范圍內。

圖1還給出了平均信息損失隨數據量增長時的變化情況。從圖中發現，數據量級的改變對平均信息損失沒有明顯的影響。

3.3.2 敏感屬性數目改變時算法信息損失

圖2所示為數據量為4 000、多樣性l=4時，EBLC算法在不同敏感屬性以及信息熵比下信息損失的變化情況。從圖中可以發現，在不同敏感屬性下，當信息熵比率控制在0.65時其平均信息損失不超過0.45，表明算法在抗攻擊性以及信息損失方面均有良好表現。同時可以看出：在相同信息熵比下， 平均信息損失與敏感屬性數目呈現正相關關系； 在敏感屬性數目相同時， 平均信息損失也與信息熵比呈正相關關系。

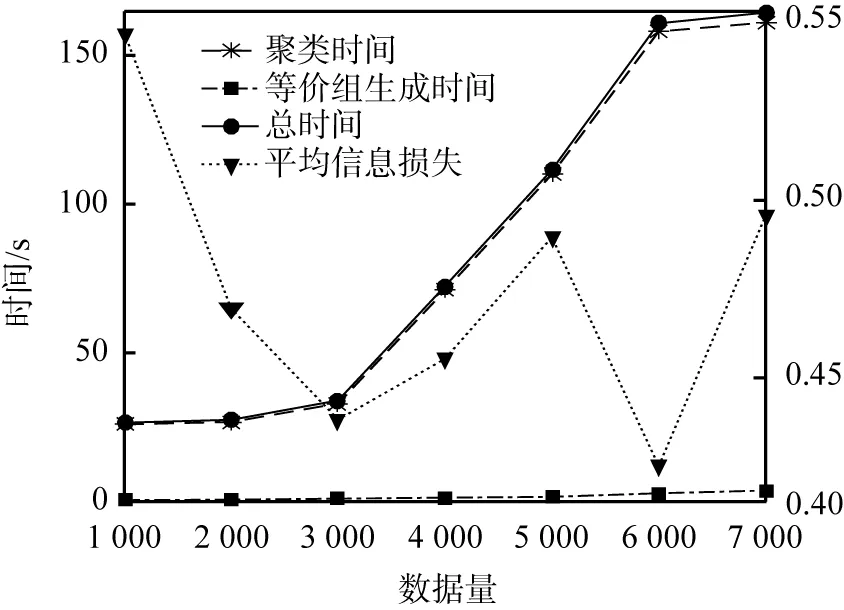
圖1 基于信息熵的l多樣性聚類算法的運行時間

圖2 敏感屬性數目變化時的信息損失

為了使新增加的敏感屬性滿足多樣性要求，在同等條件下，當敏感屬性數目增多時，原等價組元組可能需要添加新的元組，這會造成組內非敏感屬性的泛化程度提高，帶來了更多的信息損失。同時，當信息熵比率上升時，等價組中同一屬性的多樣性分布均勻度需要提升，也會導致原等價組元組數目的增加，造成非敏感屬性泛化程度提高，導致平均信息損失的增加。

3.3.3 多樣性數目改變時算法信息損失

圖3所示為數據量為4 000、敏感屬性個數m=3時，EBLC算法在不同多樣性以及信息熵比下信息損失的變化情況。從圖中可以發現，在不同多樣性條件下，當信息熵比率控制在0.65時，數據的平均信息損失不超過0.5，表明算法在抗攻擊性以及信息損失方面均表現良好。同時可以看出：在相同信息熵比下， 平均信息損失與多樣性數目呈現正相關關系；在多樣性數目相同時，平均信息損失也與信息熵比呈正相關關系。

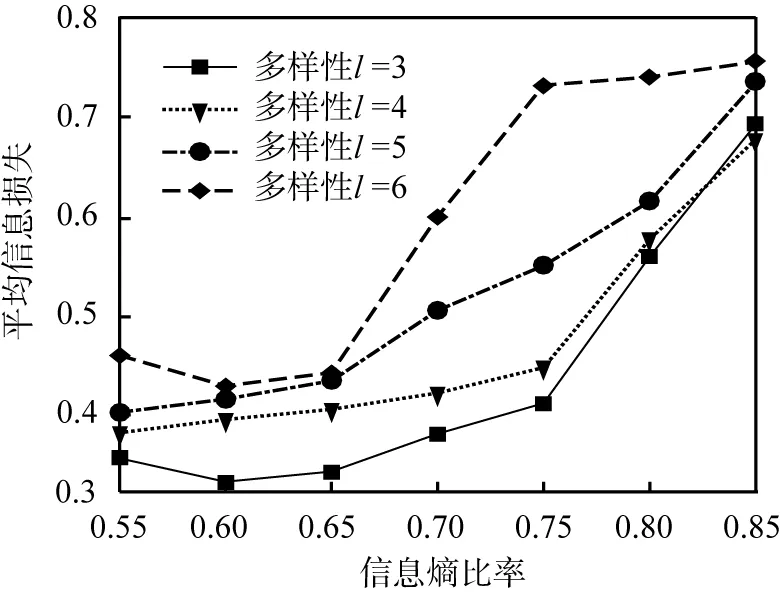
圖3 多樣性數目變化時的信息損失

在信息熵相同、多樣性數目增長時，原等價組需要添加新的多樣性元組，會造成泛化程度提高，引起平均信息損失的增加。當多樣性數目不變而信息熵比提高時，為了提高等價組內敏感屬性多樣性的均勻性，也需要向等價組添加新的元組，造成平均信息損失的增加。

4 結語

本文中基于對原數據集進行聚類分簇后從同簇內元組生成滿足(l,x,w)等價組的思路，提出了一種針對多敏感屬性數據隱私發布的ELBC匿名算法，并對其進行仿真實驗。實驗結果表明：該算法有效降低了發布后數據敏感信息易受到同質攻擊以及概率攻擊的風險，提升了數據發布的安全性；算法在不同敏感屬性數目以及不同多樣性數目條件下對數據進行匿名發布后，數據的信息損失仍然能保證在可靠范圍內，較大程度保證了發布數據的可挖掘價值。不足之處是本文中等價組內屬性的l-多樣性為語法的多樣性，在下一步工作中，將會更多地進行基于語義多樣性的算法研究。