具有通訊約束的多智能體系統的雙向一致性

，

(太原理工大學 a. 數學學院， b. 大數據學院， 山西 太原 030024)

多智能體系統的一致性因其在不同領域的廣泛應用而一直是研究者關注的焦點。例如，在工程與計算機科學中的分布式計算[1]、傳感器網絡[2]、無人機車輛編隊控制[3]和機器人團隊，以及生物學、生態學和社會科學中的羊群集體行為[4]等，已經形成了較為成熟的理論體系。在現有的文獻中，有很多關于智能體的動態行為的研究用一階微分方程進行描述[5-7]， 也有越來越多的研究者用二階微分方程描述智能體的動態行為[8-10]。

目前關于一致性問題研究的一個共同特點是關注協作系統。 各智能體通過協作進行通訊， 從而最終實現共同的狀態。 代表它們之間聯系的權重邊均非負， 然而， 在現實網絡中， 智能體之間的聯系有協作也有競爭。 例如， 在社會網絡理論中， 具有拮抗作用(既有競爭又有協作)的網絡是很常見的[11-12]。 用符號圖表示它們之間的聯系， 其中的邊可以是負權重， 因此， 其鄰接矩陣的元素可以是正的， 也可以是負的。 這是與已有研究中的通常情況的最大區別。

在具有拮抗作用的網絡中，被關注最多的還是智能體最終能否趨于共同的狀態，即一致性問題。研究[13-15]發現，存在另一種類型的一致現象，即所有的智能體會達到一個最終的狀態，大小相同但是符號相反，稱其為雙向一致或反同步。文獻[13]中引入一個合適的概念，在存在拮抗性連接的情況下，研究符號圖中的智能體如何通過分布式協議實現一致以及能達到何種程度的一致。文獻[14]中提出了一種基于事件的具有拮抗作用的多智能體系統的雙向一致性問題。利用多智能體網絡的符號拉普拉斯矩陣的譜性質，分析了系統的雙向一致性。文獻[15]中將基于集中式事件驅動控制下的雙向一致性[14]推廣到具有無向拓撲和有向拓撲的多智能體系統的分布式事件驅動控制策略，從而使所有智能體都能達到雙向一致。文獻[16]中建立了一組具有領導者的高階智能體的雙向一致性條件，所有智能體和領導者都有高階線性動態行為，智能體之間的交互拓撲由一個有向、加權的符號圖描述，得出了一組智能體到領導者狀態和另一組智能體相反的收斂性。

通訊約束是影響系統性能的關鍵因素，在實際中不能忽視。其中最普遍的是局部信息傳輸，即智能體不能將其信息完全傳輸到鄰居智能體，在這個過程中會有一部分信息丟失。現有的文獻中有很多相關研究[17-19]。文獻[17]中研究了基于局部信息傳輸的復雜動態網絡的同步分析，給出了耦合矩陣分別為對角矩陣和下三角矩陣時的同步條件；文獻[18]中針對2個目標跟蹤傳感器網絡, 提出了基于部分信息分布式濾波問題。現有的文獻中很少在智能體系統的雙向一致性問題中考慮通訊約束。

為了研究具有通訊約束的多智能體系統的雙向一致性問題，本文中在現有關于雙向一致的文獻中的控制輸入項加入信道矩陣，使得所考慮的問題更實際，從而得出系統的雙向一致性條件；首先介紹圖論知識和所要描述的問題，然后得出主要結論，再利用Lyapunov理論得出系統實現雙向一致的充分條件，最后進行數值仿真，給出一個數值實例驗證理論結果的有效性。

1 圖論知識和問題描述

1.1 圖論知識

系統中每個智能體可以抽象為一個節點。一個權重符號圖G可以由G(V,E,A)表示，其中V={1,2,…,N}為節點(頂點)集，E?V×V為有向邊的集合，A=(aij)N×N(i,j=1,2,…,N)為G的符號權重鄰接矩陣。如果邊(i,j)∈E，則A的元素aij非零，稱節點i、j相鄰。Ni={j∈V|(j,i)∈E}為節點i所有相鄰點的集合。|Ni|為Ni的基數(節點的鄰居個數)。如果任意2個不同節點間都有有向路徑，則稱G是強連通的。E+={(i,j)|aji>0}和E-={(i,j)|aji<0}分別為正邊和負邊的集合。當aji>0時，2個智能體i、j是協作關系；當aji<0時，2個智能體i、j是競爭關系。本文中不考慮節點有自環的情形，即aii=0,?i=1,2,…,N，并且總假設節點i、j之間的權重滿足aijaji≥0。IN為N階單位矩陣，1N=(1,1,…,1)T為N維向量，ON×N為N×N型零矩陣。n×n為n階矩陣的全體，n為n維向量空間為歐氏范數。圖G的拉普拉斯矩陣L定義為L=(lij)∈N×N，且lij=-aij，i,j=1,2,…,N。

1.2 問題描述

考慮有N個節點的多智能體系統，系統的每個智能體的動態描述為

(1)

式中：t為運動時間；xi(t)∈n和vi(t)∈n分別為第i個節點的位置狀態和速度狀態；ui(t)∈n為第i個節點的控制輸入。為了實現多智能體系統(1)的雙向一致性，考慮控制輸入

[vi(t)-sgn(aij)vj(t)]}，

(2)

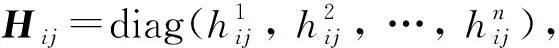
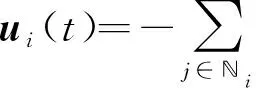
[vi(t)-sgn(aij)vj(t)]},

(3)

其中i,j=1,2,…,N。為了便于數學推導，定義信道拉普拉斯矩陣為

矩陣Rk是從Rij分解得來的。對于任意的i,j=1,2,…,N，Rk(i,j)是Rij的第k個對角線元素。顯然，Rk有行和為0的性質。本文中總是假設Rk不可約，ζk=(ζk1,ζk2, …,ζkN)T∈N是矩陣Rk對應于特征值的規范化左特征向量并且滿足根據文獻[20]，對于所有的i∈{1,2,…,N}以及k∈{1,2,…,n}，有ζki>0。令Φi=diag(ζ1i,ζ2i, …,ζni)，可以得到

定義1[13]向量δ=(δ1,δ2,…,δn)，δi={±1}是n中的一個局部象限階。一個規范變換是對n中的象限階通過矩陣D=diag(δ)進行改變。Ω={D|D=diag(δ),δ=(δ1,δ2, …,δn),δi∈{±1}}表示n中所有的規范變換構成的集合。

定義2[13]稱符號圖G結構平衡， 如果它可以把節點分為2個部分V1、V2， 其中，V1∪V2=V， 且V1∩V2=○/，使得對任意的i,j∈Vq(q∈{1,2})有aij≥0， 以及任意的i∈Vq,j∈Vp,q≠p,(q,p)∈{1,2}有aij≤0。否則，稱之為結構不平衡。

定義3[21]稱多智能體系統(1)雙向一致，如果滿足

(4)

引理1(舒爾補引理) 線性矩陣不等式

其中Q(x)=Q(x)T，R(x)=R(x)T，則該線性矩陣不等式等價于下列任一條件：

1)Q(x)>O,R(x)-S(x)TQ(x)-1S(x)>O，

2)R(x)>O，Q(x)-S(x)R(x)-1S(x)T>O。

2 主要結論

D=diag(δ),δ=(δ1,δ2, …,δN),δi∈{±1}。

則

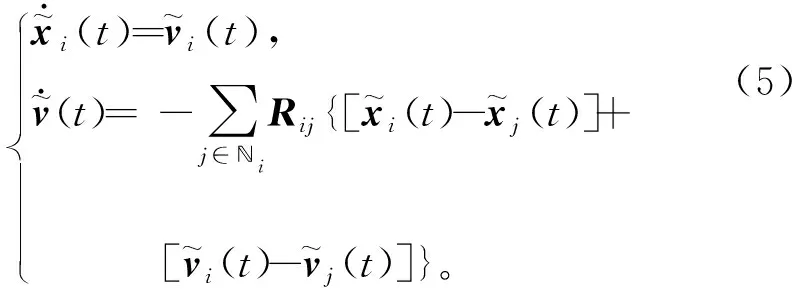
x～·i(t)=v～i(t),v～·(t)=-∑j∈?iRij{[x～i(t)-x～j(t)]+[v～i(t)-v～j(t)]}。(5)

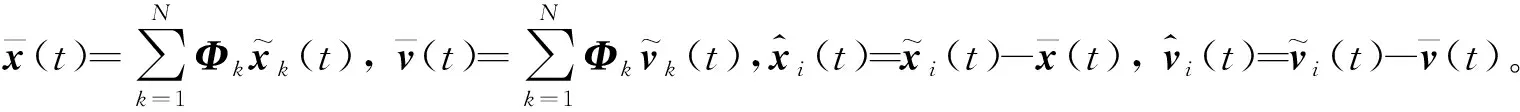
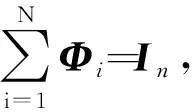
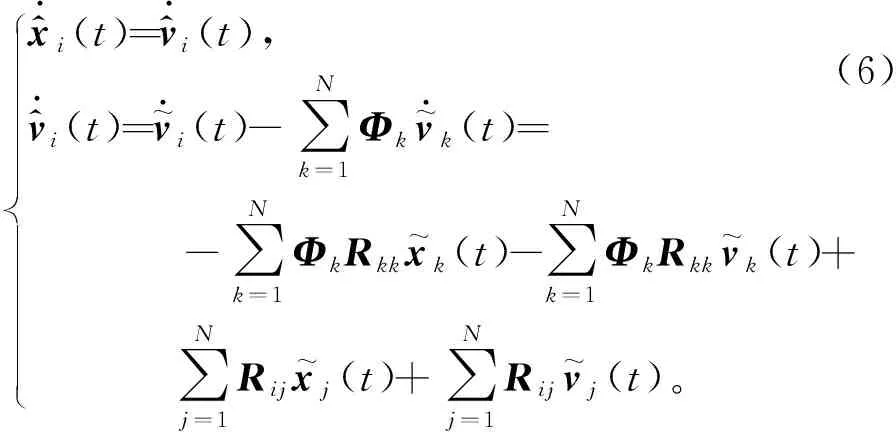
x^·i(t)=v^·i(t),v^·i(t)=v～·i(t)-∑Nk=1Φkv～·k(t)=-∑Nk=1ΦkRkkx～k(t)-∑Nk=1ΦkRkkv～k(t)+∑Nj=1Rijx～j(t)+∑Nj=1Rijv～j(t)。(6)

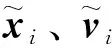
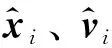
基于以上分析，可以得到多智能體系統(1)雙向一致性的條件。

定理1 假設符號圖G結構平衡，則系統(1)在控制輸入(3)的作用下實現雙向一致性，如果存在標量α>0且滿足下列的線性矩陣不等式，即對任意的i∈{1,2,…,N},k∈{1,2,…,n}，

(7)

其中

證明： 考慮Lyapunov函數

(8)

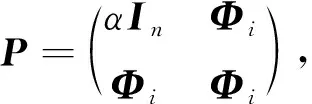
沿著系統(6)的軌跡對V(t)求導可得

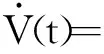
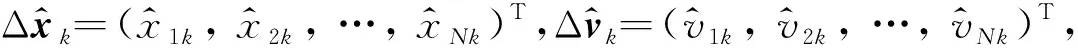
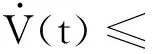
當智能體間的信息可以完全傳輸時，信道矩陣Hij=In。由Rij、Rk、Φi的定義，有Rij=|aij|In，Rk=-L，Φi=ζiIn，Wk=W=diag(ζ1,ζ2, …,ζN)， 其中，L為系統的拉普拉斯矩陣。 對任意的i,j∈{1, 2, …,N}，多智能體系統(1)的模型變為

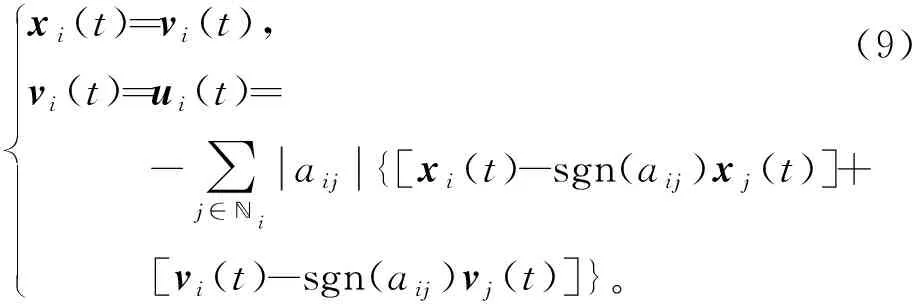
xi(t)=vi(t),vi(t)=ui(t)=-∑j∈?iaij{[xi(t)-sgn(aij)xj(t)]+[vi(t)-sgn(aij)vj(t)]}。(9)

推論1 假設符號圖G結構平衡， 則系統(9)實現雙向一致， 如果存在標量α>0且滿足下列的線性矩陣不等式， 即對任意i∈{1, 2, …,N},k∈{1,2,…,n}，

(10)

3 數值仿真

以下給出一個實例來驗證理論結果的有效性。

例1 考慮一個有5個節點的多智能體系統，每個智能體有2個維度的信息，即N=5，n=2。 每個智能體的連接情況如圖1所示，其中各智能體間的連接權重有正也有負。當權重為正時，2個智能體之間為協作關系；當權重為負時，2個智能體間為競爭關系。智能體間的連接關系用矩陣A表示,

可得D=diag(1,-1, 1,-1, 1)。給定信道矩陣H12=diag(0, 1),H15=diag(1, 1),H21=diag(1, 1),H23=diag(1, 0),H32=diag(1, 1),H43=diag(1, 1),H53=diag(1, 1),H54=diag(1, 1)。通過信道拉普拉斯矩陣的定義, 可以得出

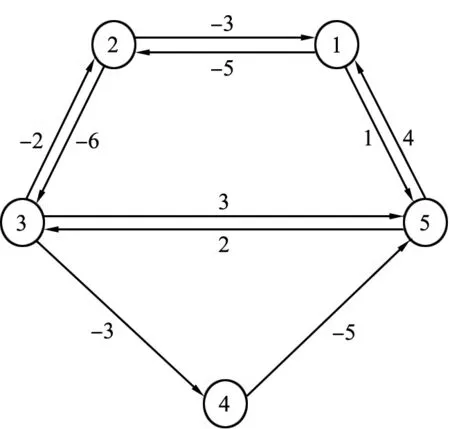
智能體3、4之間的連接-3表示智能體4可以從智能體3獲得信息，權重為3，而且為競爭關系；智能體3、5可以互相獲得信息，但是權重不同：智能體3從智能體5獲得信息的權重為2，智能體5從智能體3獲得信息的權重為3，并且是協作關系。以此類推。

利用MATLAB軟件中的線性矩陣不等式工具箱，可以得出滿足定理1中線性矩陣不等式的可行解α=1.031 2。 圖2所示為系統各節點的位置狀態， 圖3所示為系統各節點的速度狀態。 由圖2、 3可知，V1={2, 4},V2={1, 3, 5}。 屬于同一個類的智能體之間為協作關系， 它們的狀態最終會趨于一致， 而不同類中的智能體之間為競爭關系， 它們最終會趨于相反的狀態。 圖4所示為位置誤差狀態， 圖5所示為速度誤差狀態， 圖6所示為控制輸入狀態。

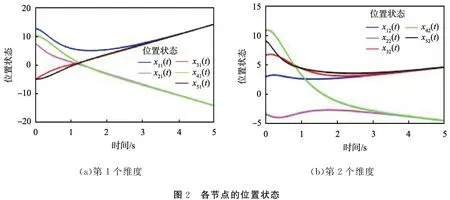
(a)第1個維度(b)第2個維度圖2 各節點的位置狀態

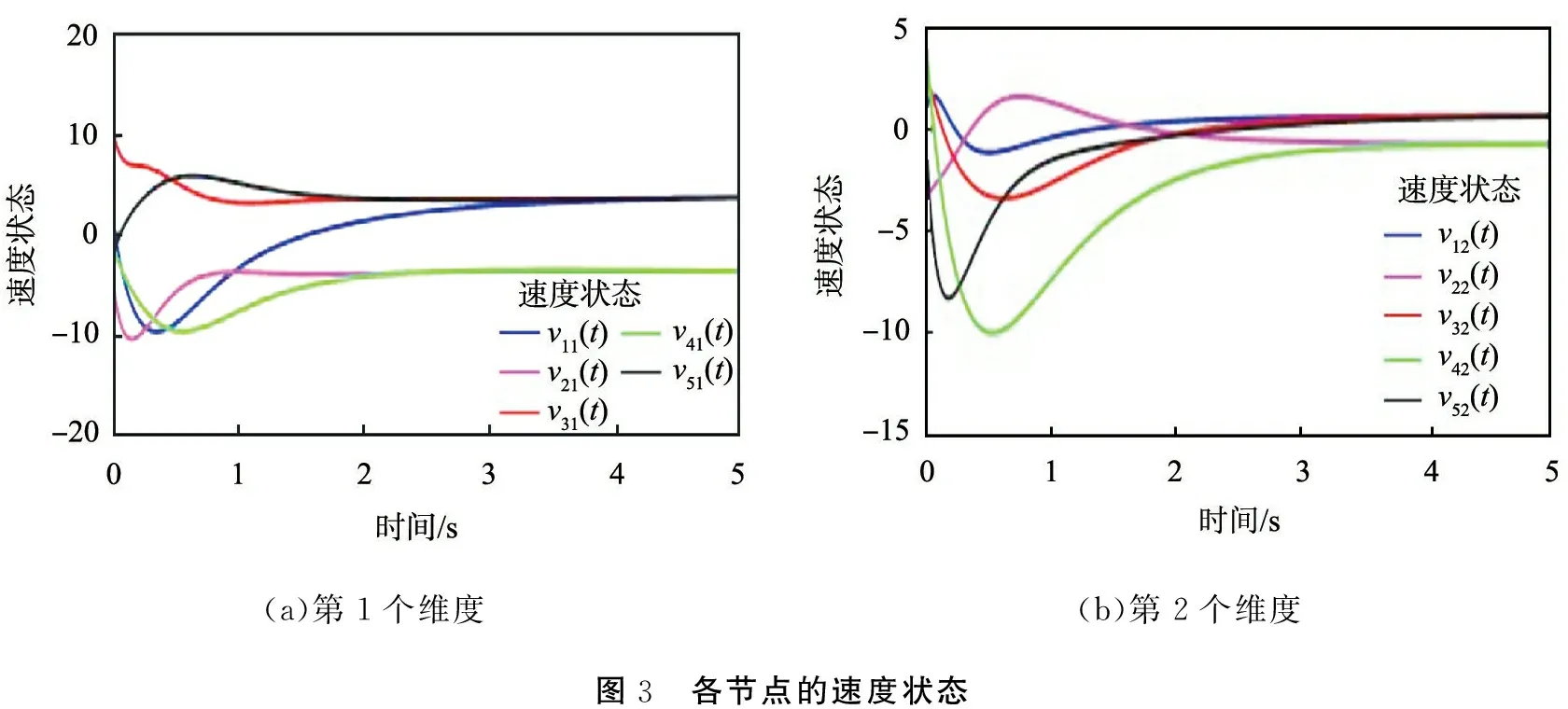
(a)第1個維度(b)第2個維度圖3 各節點的速度狀態

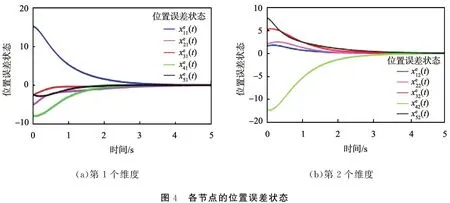
(a)第1個維度(b)第2個維度圖4 各節點的位置誤差狀態

(a)第1個維度(b)第2個維度圖5 各節點的速度誤差狀態

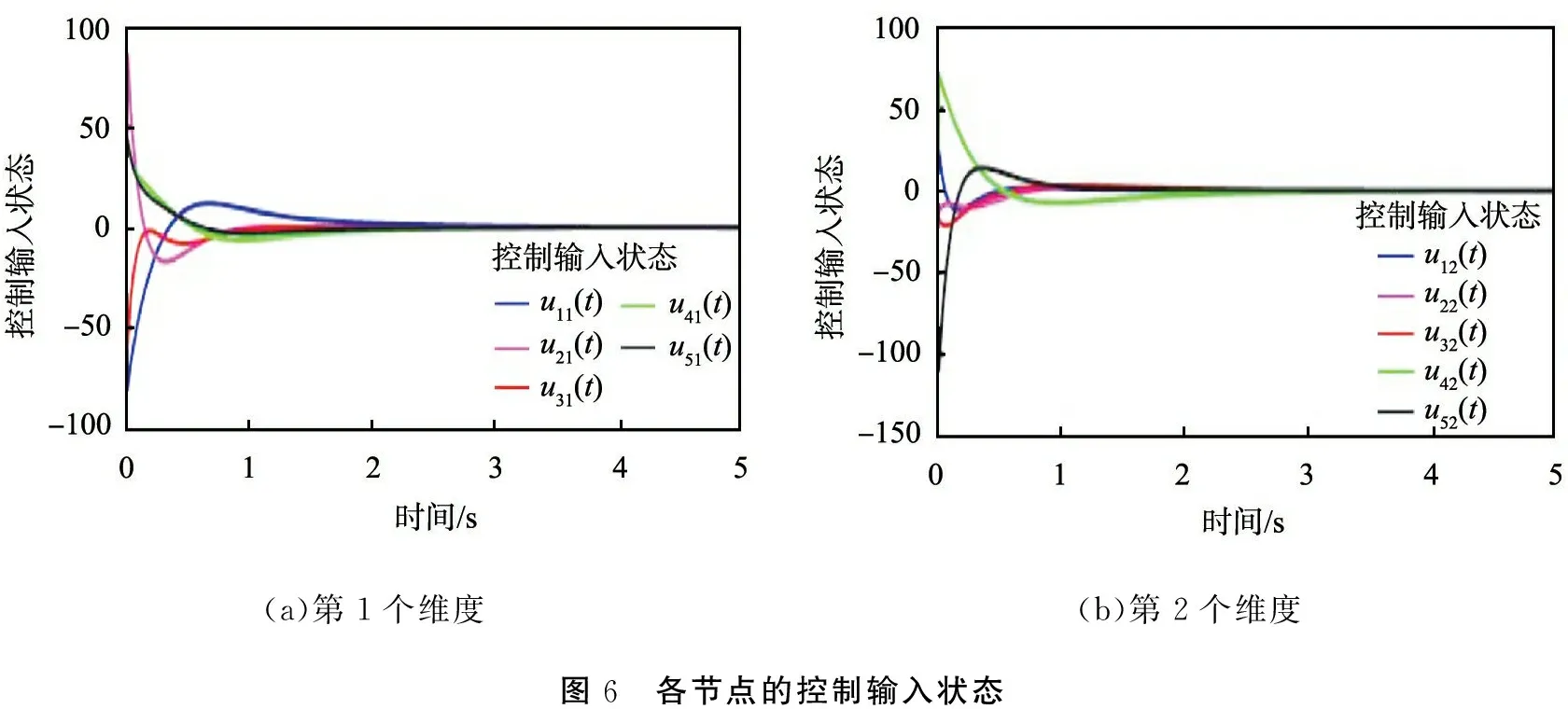
(a)第1個維度(b)第2個維度圖6 各節點的控制輸入狀態

4 結論

本文中研究了具有通訊約束的多智能體系統雙向一致性問題，通過設計合適的控制輸入以及誤差系統，將原系統的雙向一致性問題轉化為誤差系統的穩定性問題，利用Lyapunov理論得到其一致性條件。今后的研究方向是控制輸入中的對應于相對位移和相對速度的信道矩陣不相等時，實現多智能體系統的雙向一致性。