帶負載電流前饋的三相V SR的控制策略

高立東，馮麗娜

（1．泰安供電公司，山東 泰安 271000；2.山東電力設備有限公司，濟南 250000）

1 引言

擁有端口正弦電流，可調功率因數，雙向流動的能量，可調電壓的PWM技術，是能源友好型技術重點發展方向。新能源系統一直研究此項技術，特別是直驅式風力發電、光伏并網發電。PWM整流器是風力發電系統中實現機側BOOST升壓、可調功率因數和最大功率跟蹤控制（MPPT）[1-2]的關鍵技術。功率控制風力發電系統的核心，為達到最大指標功率，捕捉最大風能，利用永磁同步發電機定子磁場定向原理使發電機轉矩跟隨風速變化，實現最優輸出。

在20世紀末期，由于A.W.格林等人提出基于坐標變換的PWM整流器的連續和離散動態數學模型，使PWM整流器提升到嶄新的水平。電壓型PWM整流器主要研究電流控制的控制策略。由于三相電壓型PWM整流器拓撲結構簡單，采用相應的控制系統策略和濾波器就可以得到高品質輸出輸入電流。基于電流電壓雙環控制的三相PWM整流器一般采用間接或者直接電流控制方法。

2 數學模型

三相半橋PWM整流器主電路拓撲結構如下圖。每個橋臂是由兩個帶反并聯二極管的IGBT開關管串聯組成，共有3個橋臂。從圖中可以看出，交流側三相電壓源和三相電流分別是ea、eb、ec、ia、ib、ic；輸入側電感和輸入側等效電阻分別是 L 和 R，三個橋臂的交流輸入測電壓分別為ua、ub和uc，直流側電壓為udc，負載是 RL。

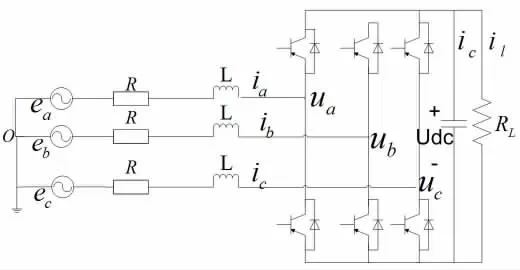
圖1 三相PWM整流器模型

首先定義單極性二值開關邏輯函數：

sj=1時uj=udc；Sj=0時uj=0；在三相靜止坐標系下根據基爾霍夫電壓定律建立回路電壓方程：

在兩相靜止坐標系下，α軸與a軸重合，變換矩陣為：

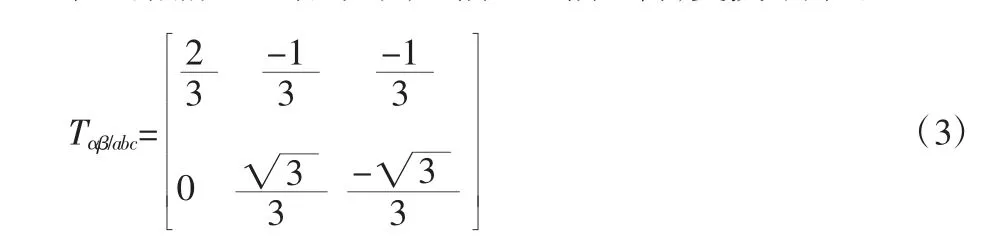
建立回路方程：

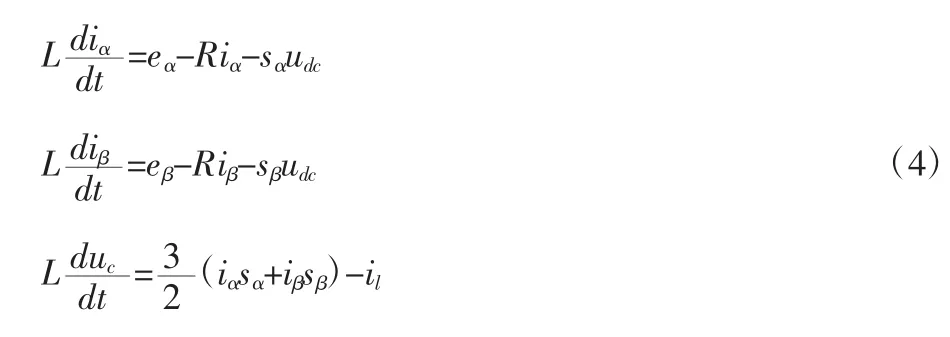
在兩相同步旋轉坐標系下建立回路方程：

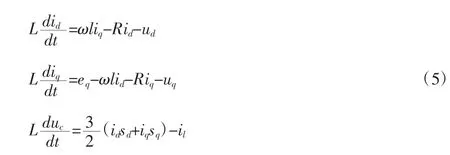
式（5）中電壓矢量定向在q軸則eq=em（電源電壓峰值），ed=0；sd、sq分別為 sa、sb、sc在 d、q 軸的等量變換；ia、ib、ic經過dq軸等量變換后為；ω為電源的角速度。在同步旋轉坐標系中id、iq分別代表無功量和有功量。系統傳遞的有功功率和無功功率分別為（6）（7）所示：

3 控制系統設計

一般的帶SVPWM雙閉環控制策略是由電壓外環和電流內環組成，內、外環的算法和物理意義明確不同；外環負責直流側電壓控制，內環負責相位差控制，保證輸出穩定直流電壓和交流輸入側的功率因數、相位差。由于電感內阻R非常小，可以忽略，控制系統框圖如下所示。

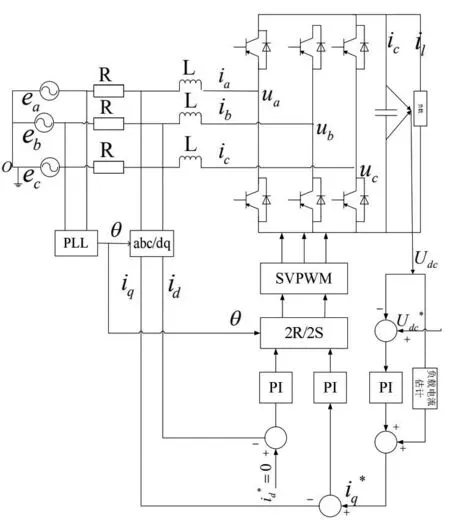
圖2 控制系統框圖

3.1 電流控制器的設計

圖3 電流環解耦控制框圖

從公式（5）可推出電流內環的傳遞函數。如圖3所示，兩個電流內環的前饋解耦算法是對稱的，可取iq為例來分析討論。在比例積分（PI）調節下電流內環iq傳遞函數如圖3所示，Ts為系統采樣周期。

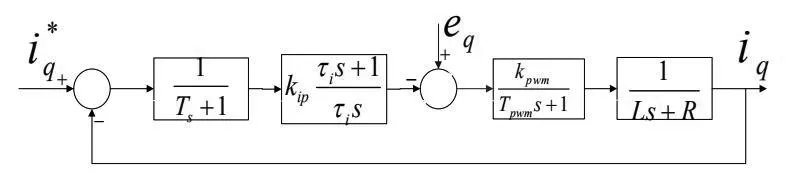
圖4 q軸電流傳遞函數框圖

為提高電流的跟隨性，系統采用型設計，使控制器的零點與被控對象極點相互對消，即

電流環開環傳遞函數為：

當ξ=0.707時系統為典型二階系統，可得：

由于開關頻率應非常高（Ts很小），所以電流內環動態響應速度高，可以把電流內環傳遞函數等效為：

3.2 電壓控制器的設計

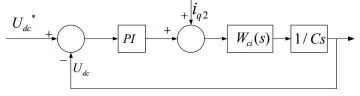
圖5 電壓環控制框圖

理想情況下整流橋的損耗非常小，可以忽略不計，當系統處于穩態運行時，電源輸入的瞬時功率等于直流母線輸出的瞬時功率。

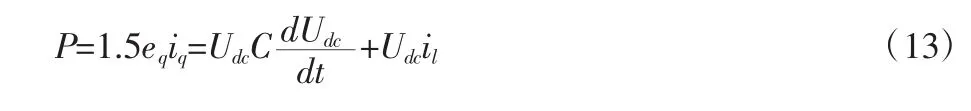
從物理意義上分析，電容電流和負載電流構成了電流iq：

其中iq1、iq2分別代表電容電流和負載電流。負載電流iq2用于前饋控制。

電壓外環使用PI控制器來維持直流電壓的穩定，可得電壓與電流的關系：

三相PWM整流橋輸出的離散且幅值不等的脈沖電流，通過電容器后，濾除雜波和毛刺后，變成負載使用的穩定直流。直流側電壓波形隨著電容器的連續充放電而不斷的波動，t1時刻Udc（t1）到t2時刻的Udc（t2），能量變化量為ΔE。

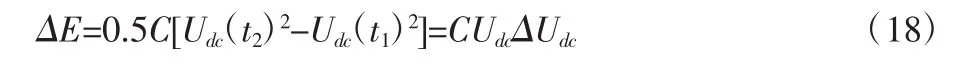
電壓的變化量ΔUdc為紋波電壓峰峰值，且ΔUdc≤0.05Udc。

輸入電源側的能量變化量：

由式（12）和（13）解得：

由式（14）得：

電壓控制器的積分系數Ki_udc可根據(22)(23)

獲得，(22)和(23)分別為零階保持器和一階保持器。由于紋波電壓的限制條件 ΔUdc≤0.05Udc，時間差（t2-t1）可以選取為三相電源周期的n倍(n<10)，這樣可以保證控制系統有效性。

3.3 負載電流il的估計

觀測圖1可知，直流母線電流是電容電流、負載電流矢量和，根據基爾霍夫電流定律可得：

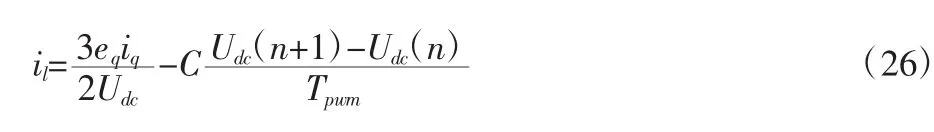
這樣通過利用直流側電壓值和微分觀測器，就可計算得到負載電流。

將式（14）離散化得：

4 仿真結果

利用Simulink中的SimpowerSystems模塊搭建三相VSR仿真模型，仿真使用電網電壓矢量定向和SVPWM調制方式，將電網電壓定向在軸，利用電網電壓瞬時值獲得電網電壓的矢量角，使用直接電流控制技術降低電流諧波含量,建立合適的微分器，估計負載電流。

本文所采用PI設計算法和負載電流的估計方法是正確的，它實現了三相整流器的單位功率因數運行，負載的電流準確估計，有效提高了整流器的抗干擾能力。

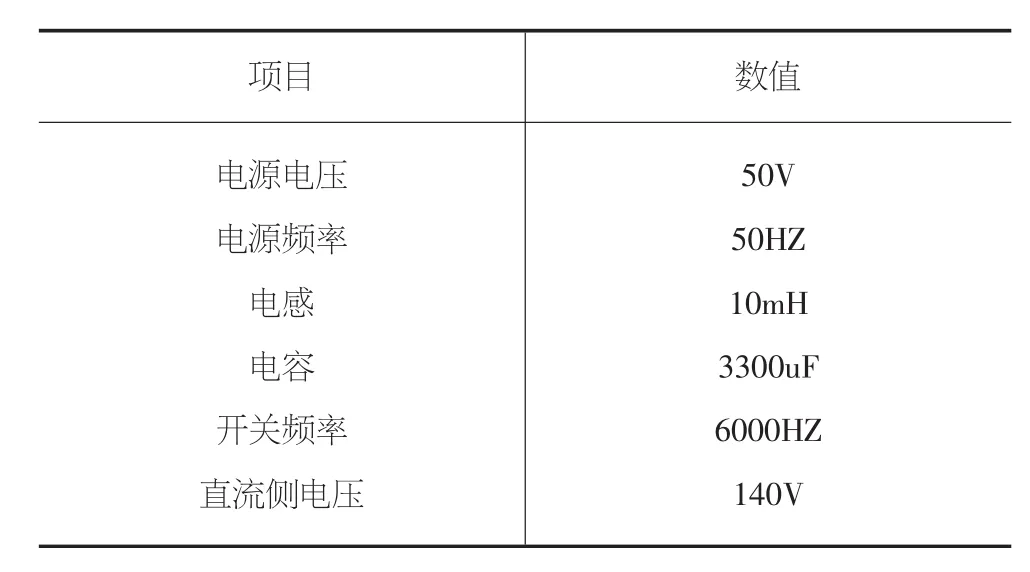
表1 模型具體參數