基于滲透二項式定律的多層織物多孔介質建模研究

代文杰， 楊恩惠， 蘇曉培， 初 曦， 王 寧， 邱 華

(江南大學 生態紡織教育部重點實驗室，江蘇 無錫 214122)

衣服需要一定保暖性和透氣性，并且進行洗滌和干燥時需要考慮織物與水和空氣之間的能量傳遞，另外在氣體的沖擊下會發生變形，所以需要對織物進行流體分析，流體分析的基礎是模型，在以往的研究中也提到了很多方法。

馬崇啟等[1]提出將一個組織循環內的紗線分為兩段并用三次貝塞爾曲線進行擬合的方法，得到紗線的軸心曲線，最后對橫截面進行掃描操作得到紗線和織物模型。這種方法得出了紗線在織物內部的彎曲形式，在紗線和織物建模中具有一定的意義，但需要復雜的數學推理，特征點的選取對模型的影響也較大，如若選取不當會產生誤差。燕春云等[2]、王旭[3]通過三維軟件進行建模，UG可以通過組織層數、經紗列數、緯紗列數、接結紗根數和接結方式等五個主要參數構造出多層織物模型。3D-Max軟件具有較好的渲染功能，主要通過布爾矩陣表示織物的經緯交織規律；通過列向量和行向量表示經浮點和緯浮點。利用三維的建模軟件可以很好地構造出織物的三維模型的外觀結構，但是無法反映紗線和織物的多孔特征。于海燕[4]將織物看做非線性柔性材料，將織物簡化為顆粒通過一定的方式連接起來形成織物模型，該模型可以很好地解決衣服的變形問題，但不能進行模擬分析得到氣流的流動特征。

由于織物內部孔隙數量多且尺度小、分布隨機，所以通過以上方法雖然可以得到紗線和織物模型，但是很難反映出織物多孔性的特征。多孔介質模型主要由骨架和大量密集成群的微小空隙構成，空隙可能相互連通，也可能部分連通，具有多孔性的特點，符合織物內多孔性的特征[5-8]。

多孔介質的數學模型表示多孔介質材料與流動空氣之間的函數關系，所以本文對織物內氣流的流速和壓降進行線性擬合得到擬合函數，利用得到的函數關系與多孔介質數學模型之間的關系，得到多孔介質模型參數。通過對織物模型進行流體計算得到模擬壓降值與實測值比較，這種方法不但簡單方便，而且模型更加符合織物多孔性的特征，此外利用得到的多孔介質模型可用有限元分析，便于研究織物的熱濕傳遞等性能[9-10]。

1 透氣性測試和結果處理

1.1 織物的規格

試驗樣品為平紋絲織物(表1)，絲織物具有良好的光澤性，平紋織物具有織造簡單，生產效率高，便于生產的優點；絲織物與皮膚有著良好的觸感，輕盈滑爽，彈性好，特別適合做貼身服裝，適合兒童嬌嫩的皮膚，具有吸濕透氣的特點，所以研究絲織物的透氣和導濕，可以更好地開發和設計絲織物。

表1 織物規格參數Tab.1 The specification parameters of fabric

1.2 測試結果和處理

織物的透氣性表示在一定的壓差下，空氣通過織物后氣流速度的大小。實驗結果會受到環境影響，所以采用標準大氣條件下(溫度25 ℃，濕度60%)，壓降表示壓差在單位長度上的變化值。

(1)

式中：P表示織物的壓降，Pa/m; ΔP表示織物兩側的壓差，Pa;h表示織物的厚度，m；n表示織物的層數。

織物的透氣性測試主要利用YG(B)461-E透氣性測試儀并根據GB/T 5453—1997《紡織品 織物透氣性的測定》標準，采用如圖1所示的實驗裝置進行透氣性測試。測試裝置主要包括：加持織物部分、測試圓環、風機。織物進行測試時，風機通過離心機使儀器內部形成負壓，織物兩邊形成一定的壓差，通過流量計得到氣流的速度。

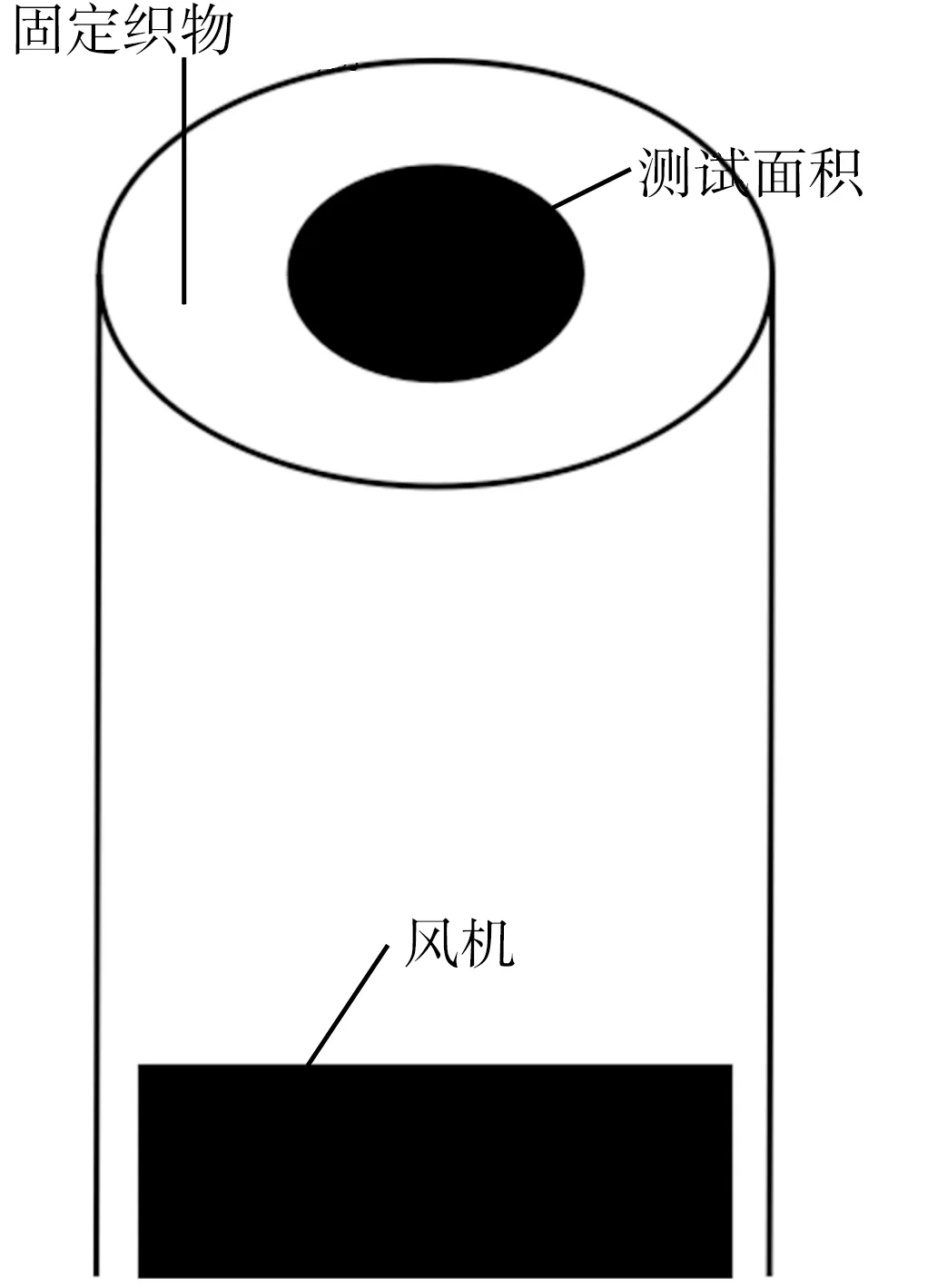
圖1 織物透氣性測試裝置Fig.1 Testing device of fabric permeability

標準規定服用織物采用100 Pa，產業用紡織品200 Pa的壓差，但是為了保證研究的適用性和實驗可行性，所以實驗采用壓差為25 Pa、50 Pa……300 Pa，織物主要由大量的纖維構成，氣流通過織物的速度較小。根據氣體在織物內部的運動，需要對織物透氣性和壓降進行二次函數擬合，得到擬合函數如圖2所示，顯示氣流速度與壓降之間呈正相關。

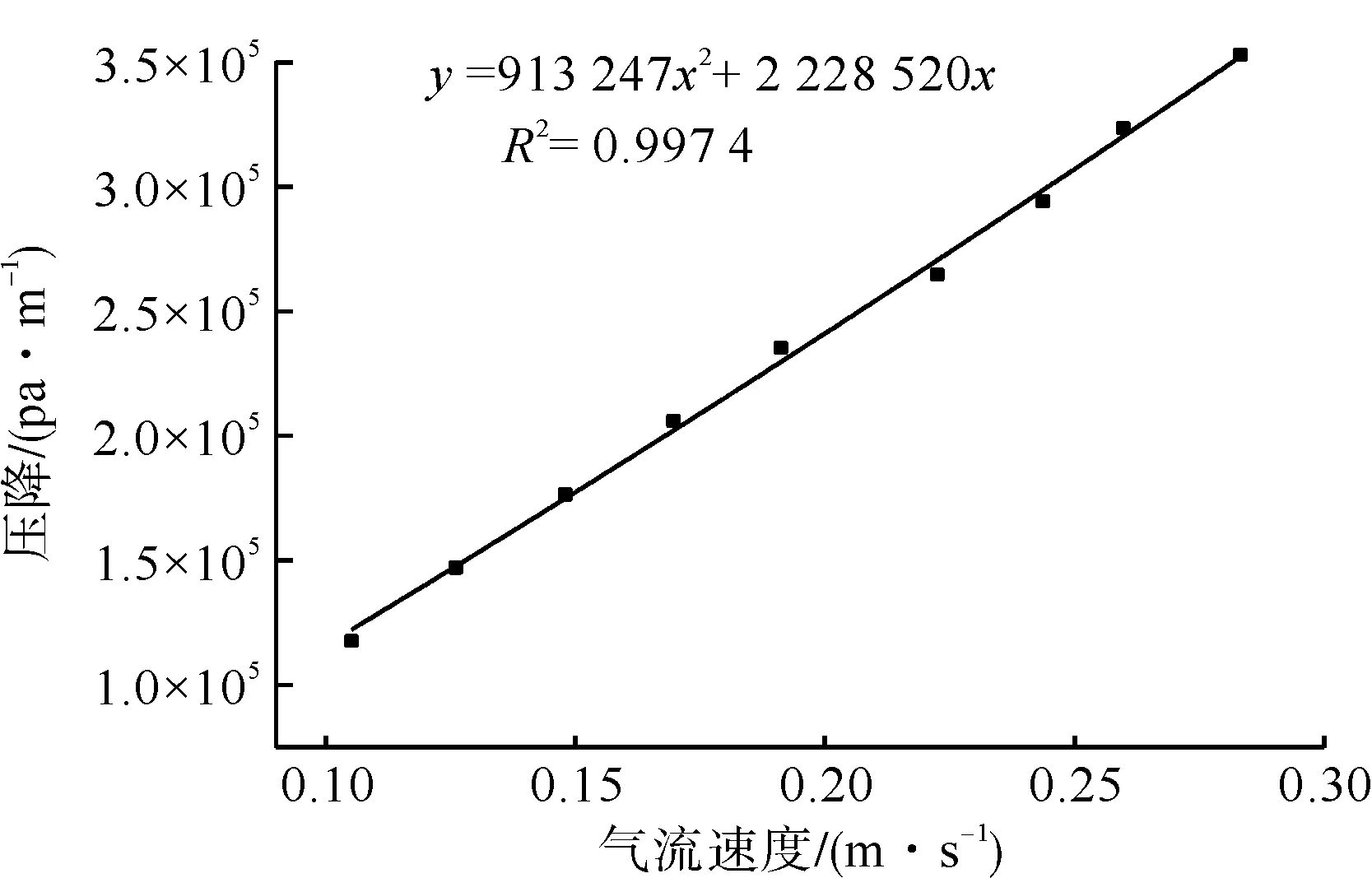
圖2 單層織物壓降與氣流速度擬合關系Fig.2 Fitting relationship between pressure drop and airflow velocity of single layer fabric

隨著織物厚度增加，氣流受到摩擦作用增加，氣流速度減小。由于各層織物之間的相對位置不同，當織物層數較小時，層數對氣流速度和壓降之間的關系影響較大；當織物層數較大時，層數對氣流速度和壓降之間關系影響減小。如當織物厚度大于三層，函數關系趨于一致，如圖3所示。所以本文通過對3～5層織物的氣流速度和壓降進行擬合分析，得到二次擬合函數：y=6.67×106x2+1.22×106x,R2=0.980 44，擬合效果較好，如圖4所示。

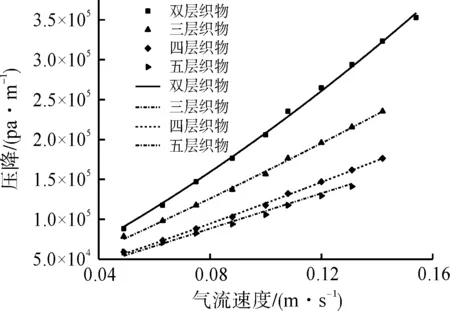
圖3 織物壓降與氣流速度擬合關系Fig.3 Fitting relationship between pressure drop and airflow velocity of fabric

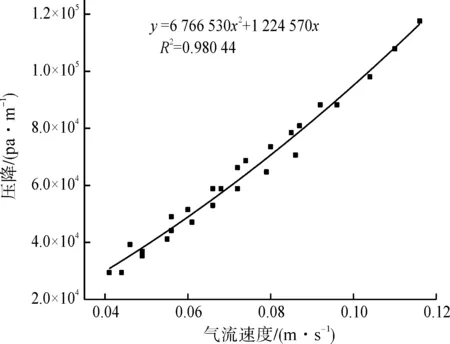
圖4 3～5層織物透氣性與壓降擬合關系Fig.4 Fitting relationship between air permeability and pressure drop of 3 to 5 layers of fabric

2 多孔介質模擬

2.1 多孔介質模型

多孔介質具有一定的滲透性，主要包括隨機排列的固體骨架，骨架會阻礙氣體或者液體的流動，并且會與液體和氣體進行能量交換[11-13]。流體在模型內部按照動量守恒和能量守恒，以及質量守恒等物理方程進行迭代計算[14]。

2.2 多孔介質內氣體的流動特征

當氣體流速較低時，流體質點作彼此平行且不互相混雜的層流運動；當流速逐漸增大到一定值時，流體的運動便成為流體質點互相混雜的紊流運動[15]。

(2)

式中：Rek表示雷諾系數；υk表示氣體的流動速度，m/s；d表示管徑，m；μ表示氣體的黏度。

雷諾系數是一個比例常數，不隨孔隙和流體物理性質而變化。當雷諾系數<2 000時，流體的流態為層流；雷諾系數>2 000時，流體的流態為紊流。當氣體的流動速度較低時，氣體的流動形式主要為層流遵循達西定律。

(3)

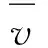
當氣流速度和雷諾系數稍大時，氣流運動除遵守達西定律外還應該考慮到慣性矩損失，如式(4)—(6)[16]所示：

(4)

(5)

(6)

式中：C2為慣性矩阻力系數；A表示線性阻力系數；B表示平方阻力系數。

根據式(4)得出，氣體分子在多孔介質中主要受到局部阻力和沿程阻力，氣流在多孔介質內運動速度與壓降之間符合二次函數關系如式(9)。

2.3 多孔介質參數

2.3.1 多孔介質孔隙率

多孔介質主要由固體骨架和孔隙組成，模型內孔隙體積對多孔介質影響較大，所以多孔介質設置時應該注意模型的孔隙率。孔隙率表示孔隙的體積與多孔介質總體積的比值，如下式所示：

(7)

式中：P表示孔隙率，%；V表示多孔介質的體積，m3；V1表示骨架的體積，m3。

由于織物結構復雜，織物的體積難以計算，所以利用重量之間的比值得到織物的孔隙率，如下式所示：

(8)

式中：Pm表示質量孔隙率，%；m表示單平方米纖維自然堆積質量，g；m1表示織物的平方米克重，g。

2.3.2 多孔介質的阻力系數

多孔介質主要研究多孔介質材料與氣體之間的函數關系，如下式所示：

J=AV+BV2

(9)

式中：J表示壓降，Pa/m；V氣流速度速度，m/s；A、B表示常數。

根據多層織物壓降與氣流速度之間的二次擬合函數關系，得到多孔介質的阻力系數。

2.4 構建多孔介質模型

為了得到準確的模擬結果，要保證氣體進入織物前要達到穩定狀態，所以氣體必須要運動一段距離(采用500 mm)達到穩定，這個距離稱作水力直徑(水力直徑一般為實驗模型直徑的4倍)。氣體作為一種特殊的介質，分子之間的距離大并且不存在剪切應力，如果受到外力會產生形變。氣體在織物內部運動時，氣體受到紗線阻礙后運動方向和大小會發生改變，其運動比較復雜。并且在流體域和多孔介質域之間存在交接面，氣體從流體進入多孔介質域時，氣體的運動會發生劇烈變化[9]。為了使織物在多孔介質內的運動達到穩定，必須適當延長多孔介質的厚度(采用20 mm)增加氣體運動的時間，所以采用如圖5所示實驗模型。

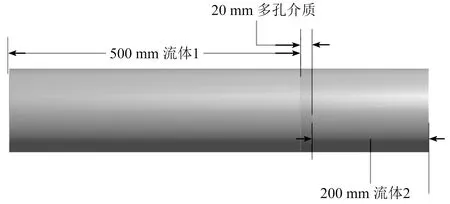
圖5 多孔介質模型Fig.5 The porous media model

多孔介質模型包括三個部分：進口：首先構建流體域；然后氣體進入多孔介質；為了得到的穩定的數據，氣體通過多孔介質后必須達到穩定(采用200 mm)。

2.5 邊界條件設置

模型的主要條件包括壁面邊界條件、進口邊界條件、出口邊界條件，由于此模型需要設置不同的域，所以在不同的域之間必須存在交界面，保證數據可以在不同的域之間進行傳遞，具體的邊界條件設置如圖6所示。

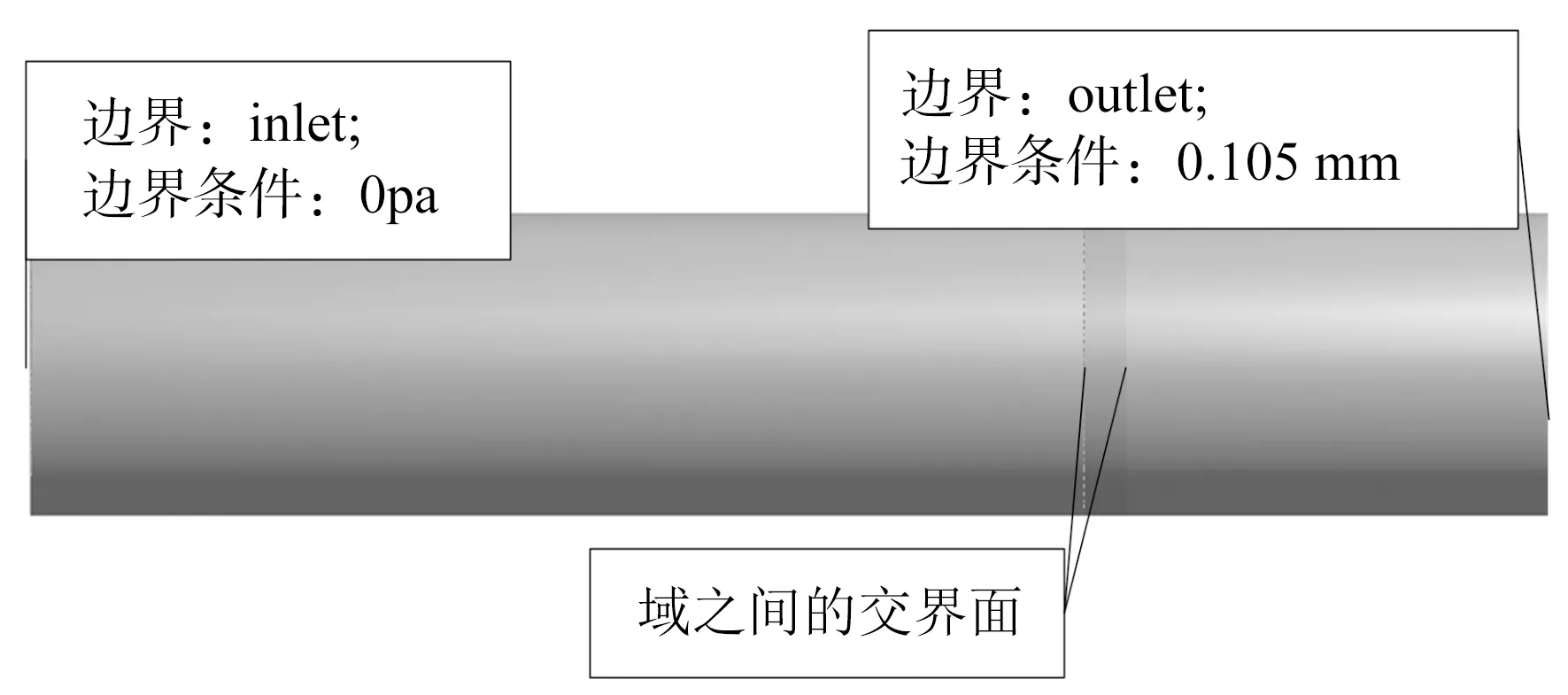
圖6 多孔介質邊界條件Fig.6 Boundary conditions of porous media

3 模擬結果和分析

多孔介質是否可以作為織物模型，需利用多孔介質進行仿真模擬計算，采集多孔介質出口壓力和入口壓力之間的壓差，將模擬得到的壓降值與測試值進行比較。由于當織物的厚度大于三層后擬合函數基本一致，所以通過模擬了1～3層織物的測試值與模擬值之間的誤差，可以驗證多孔介質是否可以用于織物模擬，如圖7—圖9所示。

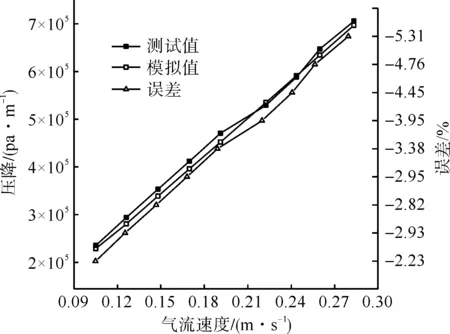
圖7 單層織物模擬值與測試值Fig.7 Simulation and test values of single-layer fabric

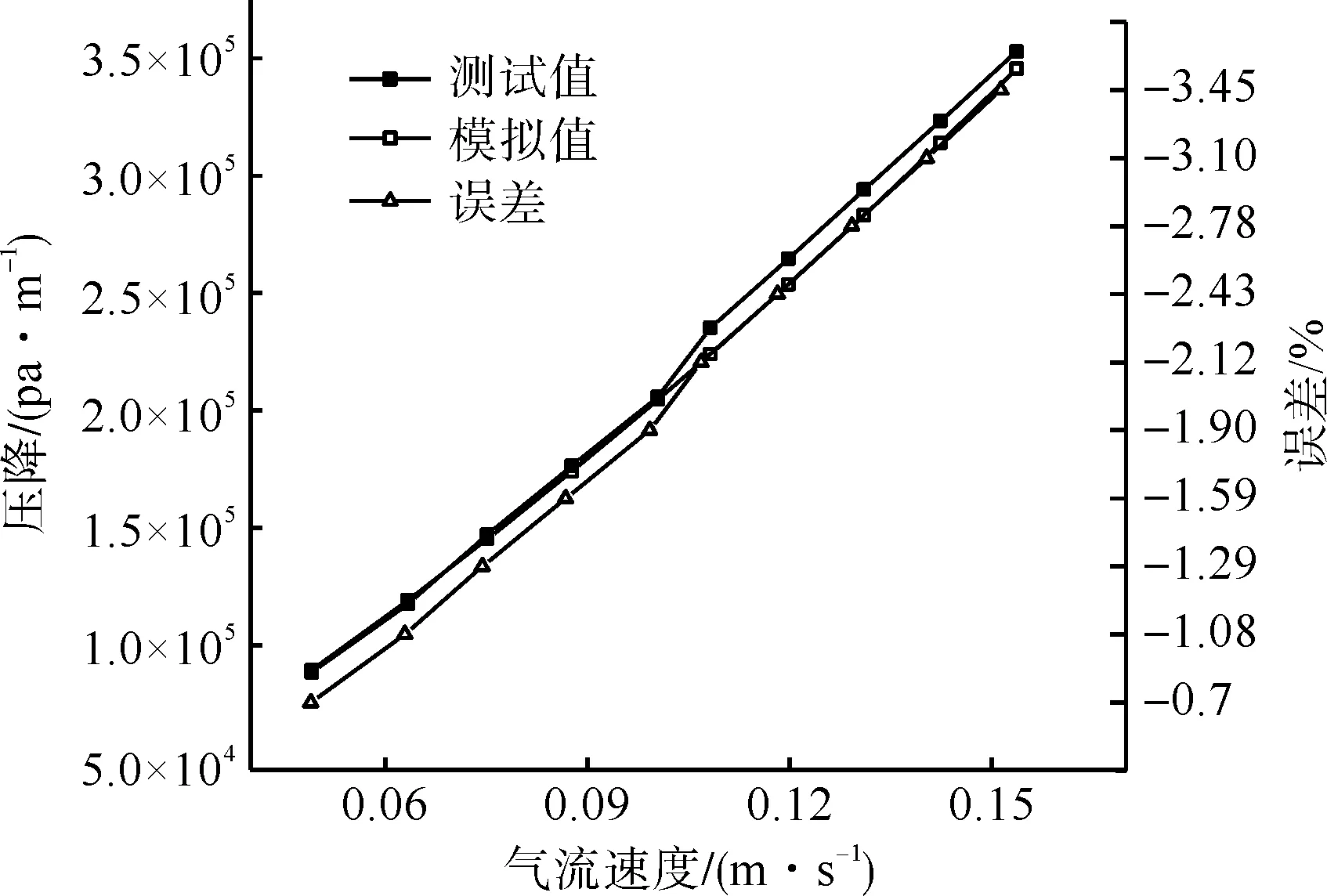
圖8 雙層織物模擬值與測試值Fig.8 Simulation and test values of double-layer fabric

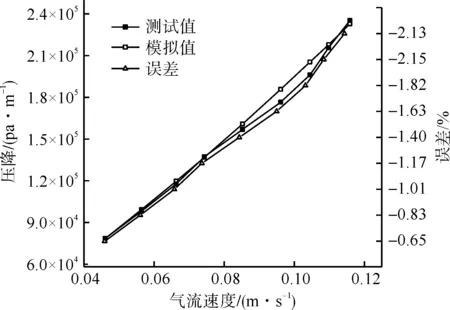
圖9 三層織物模擬值與測試值Fig.9 Simulation and test values of three-layer fabric

以上的數據分別模擬1～3層織物，得到模擬值與實際測試值之間的誤差小于6%，得出多孔介質模型可以用于1和2層織物的模擬計算，由于3層以上的織物具有相同的擬合函數，所以多孔介質模型也適用于多層織物。

4 結 論

為了構建符合織物特征的模型，首先對織物進行透氣性測試；得到壓降和氣流速度之間的函數關系；然后通過擬合多層織物的壓降和氣流速度之間的擬合關系得到擬合函數；最后驗證擬合關系是否適用于多層織物，并利用多孔介質的數學模型與擬合函數的關系，構建符合織物的多孔介質模型，并對模型進行流體計算比較模擬值與測試值之間的誤差。結果表明：織物厚度大于兩層后，得到了擬合函數：y=6.67×106x2+1.22×106x(x表示氣流的流動速度，m/s;y表示織物兩側的壓降，Pa/m)。當織物厚度6～7層時，函數值與實際測試值的誤差小于7%，所以修正函數可以表示多層織物與氣流之間的關系；模擬值和測試值之間的誤差小于6%，所以利用織物壓降與透氣性的擬合函數構建多孔介質模型可以反映織物特征，并可以用于流體模擬計算，為進一步研究織物的導熱和導濕及多種流體在織物內部流動打下基礎。