一種新的基于小波變換的QPSK信號解調方法
史俊鋒,郭華昌
(西安愛生技術集團公司,西安 710065)
在現代通信體系之中QPSK調制是使用頻率很高的一種數字調制模式。而其中相當重要的一個環節就是要對QPSK的信號進行解調。實驗證明,小波變換能夠很好的起到對于QPSK信號的表征作用,且比起傳統方式來說,這種創新的小波變換法更有優勢,對于平穩信號意外的瞬時信號也能夠很好的反映,且可以實時做出反應,精準度很高[1]。本文圍繞基于小波變換的QPSK信號解調展開研究,旨在印證該方法的優異特性,并挖掘其在更多領域的應用價值。
1 小波多尺度時頻分析原理
小波基其實并非唯一性的,還包含了尺度因子與平移因子,也就是說,信號經由小波發生變換后,可以同時得到信號的尺度和時間信息,完成對于這兩者的分析工作。盡管尺度與頻率沒有直接關聯,但實驗證明小波周期與頻率成反比。
2 小波對于QPSK信號特征的提取分析模型
2.1 小波多尺度提取分析
本文研究是基于haar小波基而展開。當QPSK信號瞬時值的跳變位置處于小波窗以外的時候,小波系數的幅值與小波平移量沒有直接關聯,且當小波尺度與載波頻率穩定不變的情況下小波系數的幅值是常數。當QPSK信號瞬時值的跳變位置處于小波窗以內的時候,小波變換系數的幅值會隨著信號瞬時值的跳變出現波動,且瞬時值位置的不同也會造成跳變信號的差異。據此得出結論,可以通過幅值數據的變動來實現對QPSK信號相位跳變的檢測。
實驗證明,瞬時值跳變度、小波尺度、信號的載波頻率等都會對小波系數的幅值造成影響。由表1可以看出,在小波尺度低于100的時候,瞬時值跳變迅速且間隔頻繁,不容易分辨。在小波尺寸超過180的時候,尺度的變化呈現靠近趨勢,依然難以分辨。而當小波尺寸處于100至180之間時,曲線的間隔較為勻稱。因此,該區間是最佳的尺度范圍。
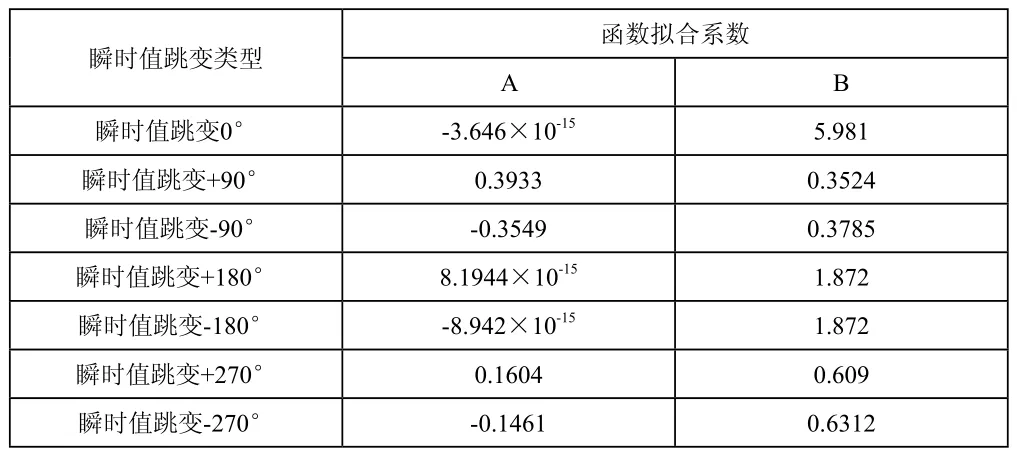
表1 小波系數與小波尺度變化曲線的擬合系數
2.2 QPSK信號的小波盲解調
QPSK信號的基帶信號的組合形式總共可以形成16種。各組基帶信號與組合序列具有關聯性。所有基帶信號的組合除了和本身序列具有較強關聯,還會與另外一個的基組形成較強的關聯,呈現一定的規律。
3 仿真結果分析
3.1 小波基的差異對QPSK信號盲解調的影響
小波基的差異會形成小波變換時段頻率的不同分辨率。其正交性特點有效儲存了QPSK信號的所有能量。小波的對稱性可以有效降低信號瞬時值的邊緣效應。此外,小波的強度會隨著支撐集的減小而增加。
本文研究采取了仿真實驗的方法,來檢驗小波基在各種信噪比噪聲下的能夠實現的盲解調的具體情況,選取了6種小波基在0至20dB的噪聲環境下對QPSK信號進行小波變換操作和盲解調,同時提取出尺度在5-20之間不同尺度的小波系數[2]。實驗結果證明,信號解調的準確率隨著信噪比的增大而提高,不同小波基所反映出誤碼率有所差異。
3.2 小波尺度的不同優化組合形式
采取仿真實驗的方式,進一步展開對于小波尺度之間的各組優化組合形式的研究。仿真過程中,對QPSK信號加噪,以bior1.1為小波基,將小波尺度控制在1:30。實驗結果表明,采用多尺度小波變換的方式可以提供盲解調的精準率。同時也可以有效結合QPSK信號的乘積特征,有效減輕噪聲的干擾。當信號處于小尺度的時候,能夠充分提取信號頻率較強的部分,當信號處于較大尺度的時候,可以有效提取信號頻率較低的部分。
4 結束語
綜上所述,作為現代通信中使用頻率相當之高的一種數字調制模式,具備了一系列的優勢特點,在無線通信領域得到了非常廣泛的應用。展開對于QPSK信號解調的深入研究具有非常積極的意義。本文研究建立在小波變換的QPSK提取分析模型的基礎上,對QPSK信號的盲解調提出一種創新的方式。仿真實驗證明,這種創新的方式有效解決了傳統解調無法做到的實時性的問題。經過對QPSK調制信號展開、提取和分析,該信號解調新方法具備十分出色的抗噪性能。與傳統的QPSK相干解調方式的不同之處在于,它采用具有多分辨特性的時頻分析法,能夠直接判斷接收到的信號頻率與瞬時值,并且能夠實現盲檢,不需要接收信號與發送信號的同步性。該方法比起傳統信號解調法有著非常明顯的優勢,值得在更多領域之中擴大應用。

