時序耦合約束下的多無人機協同任務決策研究

張耀中, 陳嵐, 史國慶, 郭操

(1.西北工業大學 電子信息學院, 陜西 西安 710072; 2.沈陽飛機設計研究所, 遼寧 沈陽 110035)

無人機(unmanned aerial vehicle,UAV)具有隱身性好、自主能力強、可重回收等特點,能夠代替有人機執行“枯燥、惡劣、危險”的任務,減少參戰人員的傷亡,降低裝備和使用成本等,其軍事地位正不斷提高,逐漸成為現代戰場上的重要作戰力量[1]。早期的無人機由于功能單一通常執行戰場目標偵察、跟蹤、監視等單類型任務,隨著無人機平臺以及各類載荷技術的快速發展,無人機的功能不斷完善,任務能力不斷增強,已經逐步轉化為能夠執行一系列復雜任務的多用途空中作戰平臺,如壓制敵防空系統(suppression of enemy air defense,SEAD)、電子攻擊、滲透式偵察/打擊等任務。SEAD主要指對特定區域的敵方防空系統(預警雷達站、地面防空導彈雷達陣地以及通信/指揮控制站等)實施打擊摧毀,使其暫時或永久失去作戰能力,從而極大削弱敵方的防空力量[2]。

在SEAD作戰任務中,假定每個目標都已事先偵察確認,則需要無人機分別對這些目標執行打擊和毀傷評估2類子任務[3]。且打擊任務完成后必須在特定的時間內執行相應的毀傷評估任務,因此這2類子任務間具有特定的時序耦合約束關系。

如何有效執行特定時序耦合約束下的多個任務已經成為當前無人機協同打擊領域的研究熱點問題之一。國內外的研究者提出了不少相應的解決方案,并取得了一定的成果,如文獻[4]以多無人機協同執行搜索——打擊任務為背景,提出了一種PTCFA聯盟組建算法,在搜索到目標時,由leader組建針對該目標的打擊聯盟和毀傷評估聯盟,同時滿足相應的約束條件,是一種比較有效的分配方法,但是該算法對無人機資源約束做了較多的簡化處理。文獻[5]對集中式控制和分布式控制進行比較后認為當無人機執行相互約束性強的任務時,集中式控制往往能獲得更好的性能。文獻[6]同時考慮了多無人機的空間協同約束、任務執行時序約束和時間約束等多類協同約束關系,給出了求解策略,但算法搜索空間巨大,難以在有效時間尋找最優解。文獻[7]考慮了單任務規劃中的優先級約束,規定具有較低優先級的任務必須在具有較高優先級的任務執行之后才能被分配,但算法在考慮2種以上任務類型時的尋優時間隨著任務的增多而呈指數增長,大規模動態任務規劃難以實現。文獻[8]采用分布式方法建立了具有時序約束的任務分配模型,將任務按優先級分層,運用擴展的一致性束算法進行求解,對比集中式算法,求解結果相對較差但可行。文獻[9]針對多異構無人機協同任務規劃問題構建了分層控制算法,在考慮無人機的異構性、資源有限性以及任務多樣性等復雜約束條件下,針對任務中存在的死鎖問題提出了一種基于圖論算法的解鎖方法,取得了較好的效果。

通過對相關文獻的分析可以看出,目前對耦合約束特性下協同任務決策問題的研究已經取得了不少成果。但是由于任務間特定的耦合關系導致任務分配過程具有一定的復雜性,針對特定任務時序耦合下協同分配問題的研究仍然較少。本文通過研究多異構無人機協同執行SEAD任務過程中存在的時序耦合約束,提出了一種基于遺傳算子的離散引力搜索算法(GSA-GA)對問題進行求解,通過仿真驗證了算法的有效性,并采用蒙特卡羅仿真實驗與離散粒子群算法(DPSO)進行了對比,仿真結果表明該算法具備更好的收斂性和更快的收斂速度。

1 具有時序耦合約束時的協同任務決策問題建模

1.1 問題描述

設有3種類型(約定為A/B/C型)共M架無人機,無人機配置信息如表1所示,用集合U={U1,U2,…,UM}表示。任務場景中有N個待摧毀目標,用集合T={T1,T2,…,TN}表示,要求無人機在任務航程最短約束下對所有目標執行打擊和毀傷評估2種任務,要求目標必須在打擊任務完成后的特定時間約束內完成相應的毀傷評估任務。

表1 無人機配置信息表

1.2 目標函數

在無人機執行SEAD任務時要求無人機在任務區內飛行的時間越短越好,因此,以最小化所有無人機中的最大任務航程為目標函數,定義如下:

F=min(maxVi)i=1,2,…M

(1)

式中,Vi表示第i架無人機的任務航程。i=1,2,…M為無人機編號。

假設無人機在任務執行過程中的飛行高度和速度恒定,則第i架無人機的航程為:

Vi=vi×(eTni-sTni)+D(Tni,BP)

(2)

式中,vi為第i架無人機的速度;eTni為任務Tni的完成時刻;sTni為任務Tni的開始執行時刻;D(Tni,BP)為任務Tni與基地BP的歐式距離,計算公式為:

(3)

xBP,yBP,xTni,yTni分別為基地BP與任務Tni的位置坐標。

(4)

pi表示第i架無人機的初始位置,Ti(ni-1,ni)表示第i架無人機從任務ni-1所在的位置飛向任務ni所在位置需要的時間,其計算公式為:

(5)

1.3 約束條件

時序耦合約束下協同任務決策問題中的約束條件如下:

1) 確保每個目標的打擊和毀傷評估任務都能被執行:

(6)

(7)

Tjh為目標Tj的第h類任務(h=1,2),h=1表示打擊任務,h=2表示毀傷評估任務。

2) 確保每個任務只能被執行1次:

(8)

3) 確保每架無人機至少被分配1個任務:

(9)

4) 滿足任務執行的時序耦合約束:

sTjh+xijh*tijh≤eTjh

(10)

eTjh≤sTj(h+1)

(11)

tijh為無人機Ui執行任務Tjh的任務執行時間;sTjh表示任務Tjh的開始執行時刻,eTjh表示任務Tjh的完成時刻。

5) 航程約束:

Vi≤Vmaxi

(12)

Vmaxi為無人機Ui的最大航程。

6) 武器載荷資源約束:

(13)

Ri為無人機Ui攜帶的武器載荷數量。

7) 打擊任務和毀傷評估任務的時序約束:

eTj1+Inter-min≤sTj2

(14)

eTj1+Inter-max≥sTj2

(15)

Inter-min和Inter-max分別為打擊任務和毀傷評估任務間的最小和最大時間間隔。

2 基于遺傳算子的混合引力搜索算法

2.1 引力搜索算法

引力搜索算法(gravitation search algorithm,GSA)是由克曼大學教授Esmat Rashidi等人在2009年提出的元啟發式優化算法,其本質是模擬自然界中的萬有引力現象,并將其演化成隨機搜索最優解的過程[12]。GSA算法的原理如下:

1) 個體表示:

假設在一個D維搜索空間中,存在N個個體構成的群體,第i個個體的位置為:

(16)

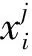
2) 質量計算:

每個個體的慣性質量由個體所在位置所決定的適應度值決定,在t時刻,個體Xi的質量用Mi(t)表示,計算公式如下:

(17)

式中,fi(t)表示個體Xi在t時刻的適應度值,b(t)和w(t)分別表示在第t次迭代中所有GSA個體的最好適應度值和最差適應度值。

3) 引力計算:

在t時刻,個體i和個體j之間在第l維的萬有引力計算公式為:

(18)

式中,Mpi(t)表示在t時刻個體i的被動引力質量,Maj(t)表示在t時刻個體j的主動引力質量,s是防止分母為0的控制常量,Rij(t)為個體i和個體j在t時刻的距離。G(t)表示t時刻的引力常數,它由開始的某一初始值,隨著時間的推移,迭代步數的增加不斷地減小,其計算公式為:

(19)

式中,T表示最大迭代次數,G0和α為固定常數。參考文獻[13],通過多次試驗數據表明G0取100,α取20時算法具有最好的收斂性能。

Rij(t)表示個體i和個體j在t時刻的距離:

Rij(t)=‖Xi(t),Xj(t)‖

(20)

式中,Xi(t)和Xj(t)分別為個體i和個體j在t時刻的位置。而在t時刻,個體i在第l維上受到的合力等于其他所有個體對其作用力的總和,計算公式如下:

(21)

4) 位置更新:

引力搜索算法來源于對萬有引力現象的模擬,它遵循經典的牛頓第二定律。當個體受到其他個體的引力作用后會產生相應的加速度,因此,根據公式(20)計算得到的引力以及牛頓第二定律,個體i在第l維獲得的加速度等于其受到合力與其自身慣性質量的比值,計算公式為:

(22)

式中,Mii(t)為個體i在t時刻的慣性質量,其值等于(17)式中的Mi(t)。

每一次更新過程中,個體根據引力產生的加速度更新自身的速度和位置,更新方式如公式(22)所示:

(23)

2.2 個體編碼模式

針對問題特點,我們采用了一個4N維的數組表示一個個體,分為2部分:任務分配(task allocation)部分和任務排序(task sequencing)部分,其中個體的前2N維為任務分配部分,余下2N維表示任務的排序方式。

任務分配部分表示了N個目標共2N個任務的分配結果,即哪個目標的哪個任務分配給哪架UAV。該部分共有2N個位,由N個目標依次按照目標編號排列,從第一個位開始,每兩個位代表一個目標,其中第一個位表示攻擊任務,第二個位表示毀傷評估任務。每個位的取值為當前位所代表任務可供選擇的UAV順序編號,有效保證了各任務被分配給能夠執行該任務的UAV。

任務排序部分表示了所有任務的排序情況,由2N個位組成,每個位由目標的編號編碼,每個目標的編號出現2次,出現的順序表示該目標兩個任務間的先后順序,目標編號i出現的第j次,表示該目標的第j個任務。設定j=1表示攻擊任務,j=2表示毀傷評估任務。如此編碼,可保證攻擊任務和毀傷評估任務的時序耦合約束。

2.3 個體解碼模式

個體信息的解碼是在編碼的基礎上,采用相反的處理模式,將編碼得到的數據通過一定的方式轉換成所求解問題的可行解決方案,用解碼得到的數據計算出當前方案的適應度值,即目標函數值,并通過目標函數值的大小評判當前解決方案的優劣。

算法的具體解碼步驟如下:

Step1 對個體的任務分配部分進行解碼。

1) 初始化各無人機的任務集合為空集,即Tsequencei=?;

2) 從左至右依次讀取第k位上的值i,若k為奇數,則j=(k+1)/2,h=1;若k為偶數,則j=k/2,h=2,將Tjh加入到Tsequencei中。

Step2 對個體的任務排序部分進行解碼。

1) 從左至右依次讀取第k位上的值j,每個j代表的是目標Tj上的一個任務,若j是第h次出現,則表示Tjh。當k=2N得到所有任務的排列順序Ts;

2) 將Tsequencei根據Ts重新排列任務順序,當Tjh和Tkl都在Tsequencei中時,將兩者按照Ts中的先后順序重新排列。

Step3 輸出各無人機的任務執行序列Tsequencei。

2.4 種群初始化與個體更新策略

以隨機數方法對每個個體進行初始信息賦值。對于個體中的任務分配部分通過(23)式更新個體的位置和速度,更新后的個體位置需要進行可行性修正。首先對每一位的值采用四舍五入的方法進行取整,其次,對取整后的每一位進行合法性判斷,若該位的取值不在該位表示任務的可執行無人機集合內,則采用就近原則,以集合的邊界元素代替。

對于任務排序部分的更新,本文引入遺傳算法中的交叉和變異操作對該部分進行更新。

1) 交叉:交叉操作是利用父代個體經過一定的操作組合后產生新個體,從而達到在不破壞有效模式的前提下對解空間進行高效搜索的目的。采用改進的POX交叉方法,對個體的任務排序部分進行交叉操作,進而達到更新的目的。改進后的POX交叉操作每一次只產生一個新個體,算法步驟如下:Step1:從目標集{T1,T2,…Tn}隨機抽取一個目標子集Tset;

Step2 選擇需要進行交叉操作的個體X1和X2,若X1的適應度函數優于X2,則將X1中包含在目標子集Tset中的目標復制到新的個體C中,保持位置和順序不變;

Setp3 將X2中不包含在Tset中的目標復制到C中,保持順序不變;

Step4 若新個體C的適應度函數優于X2,則保存新個體,并替代原來的個體X2。如圖1所示,含有4個目標,隨機抽取的目標集Tset={2,3},X1要優于X2,將X1中包含目標2,3的位復制到新個體C中,然后將X2中去掉目標2,3后,剩下的部分按照原來的次序依次復制到C的除去2,3所在位的其他位,從而產生新個體C。

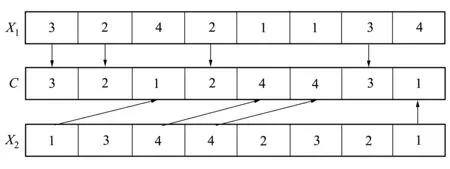
圖1 POX交叉操作

2) 變異:變異操作是通過隨機改變個體的某些位,從而產生較小擾動生成新個體,增加種群多樣性,在一定程度上控制引力搜索算法的局部搜索能力。我們采用基于鄰域搜索變異操作,在個體的任務分配部分不變的情況下,采用基于鄰域搜索的變異方法,能夠更好地通過局部范圍內的搜索找到適合任務分配部分的任務排序,從而改善子代性能。其算法操作步驟如下:

Step1 在個體的任務排序部分隨機選擇r個位,并生成其排序的所有鄰域;

Step2 計算所有鄰域的適應度函數值,選出最佳個體作為子代,并代替原來的個體。

引入遺傳算子改進后的混合引力遺傳搜索算法(GSA-GA)的處理流程如圖2所示。

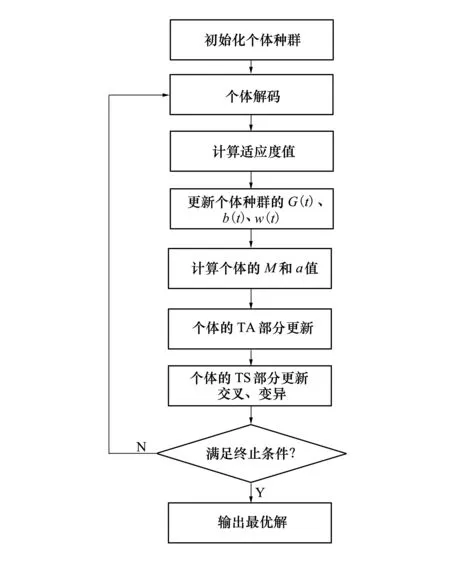
圖2 GSA-GA算法流程圖

3 仿真算例與分析

設定任務場景中有5架UAV和9個待摧毀目標,無人機相關信息如表2所示。

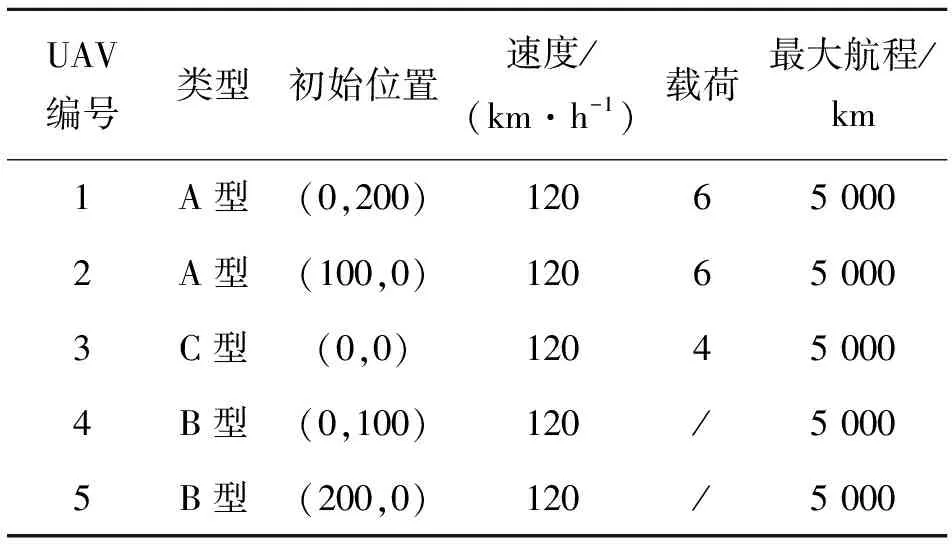
表2 無人機相關信息

目標及返回基地信息如表3所示。假設無人機執行完成打擊任務的時間為0.05 h,執行完成毀傷評估任務的時間為0.1 h,且毀傷評估任務和打擊任務的最小時間間隔為0.1 h,最大時間間隔不能超過0.5 h。

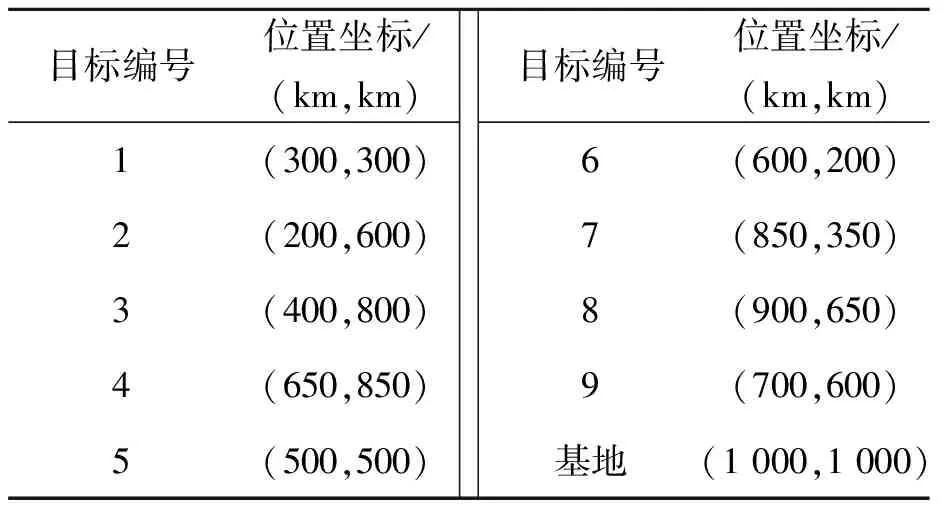
表3 目標及基地位置信息

基于以上作戰想定,采用改進的引力搜索算法進行仿真,種群規模為30,最大迭代次數為100次。仿真得到最優任務分配結果如表4所示,各子任務被執行時刻如表5所示,圖3為最優任務分配結果下的無人機執行任務過程示意圖。

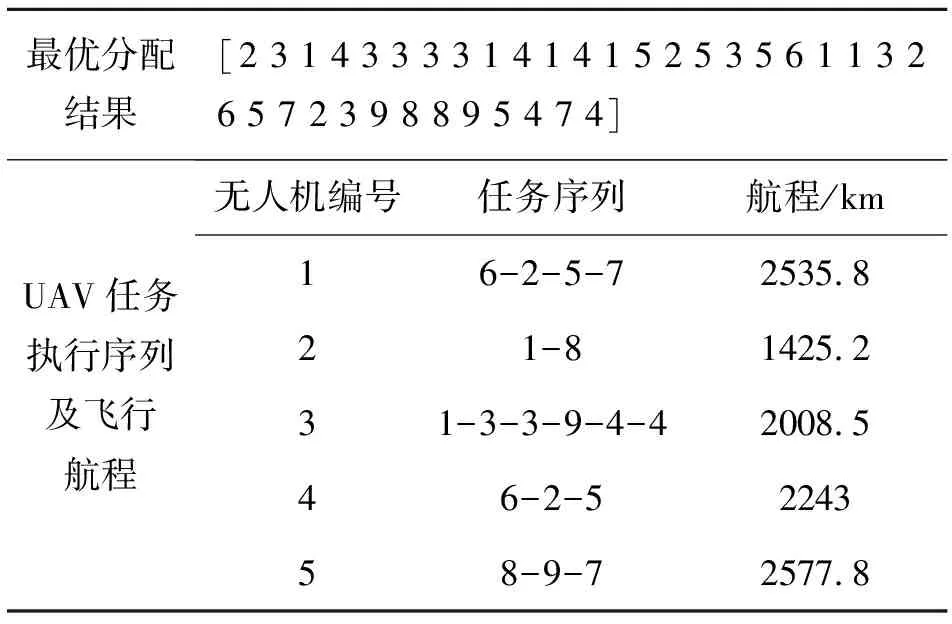
表4 最優分配結果

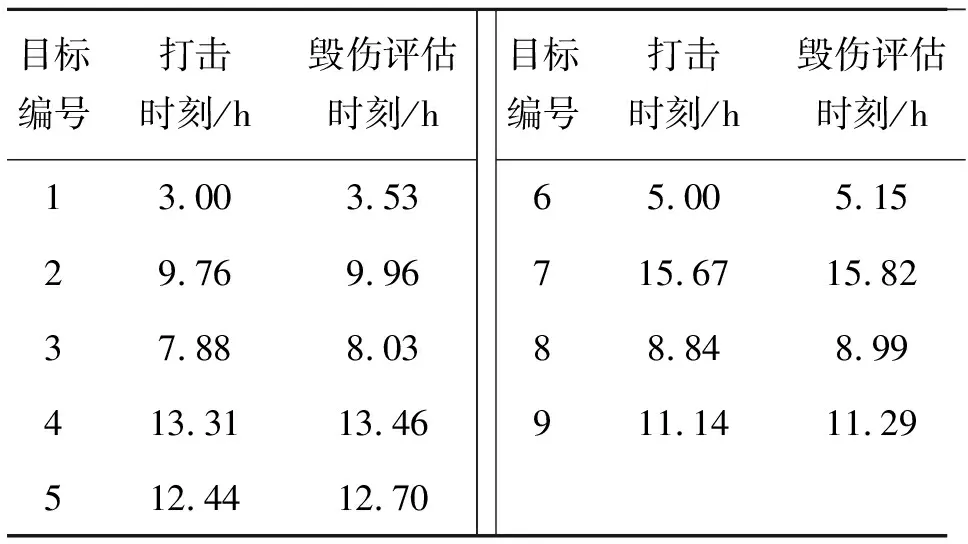
表5 任務執行時刻表

由表4可以看出,分配結果中各UAV的資源約束和航程約束是完全滿足的,由表5可以看出,各目標的打擊與評估任務是滿足任務間的時間耦合約束的。

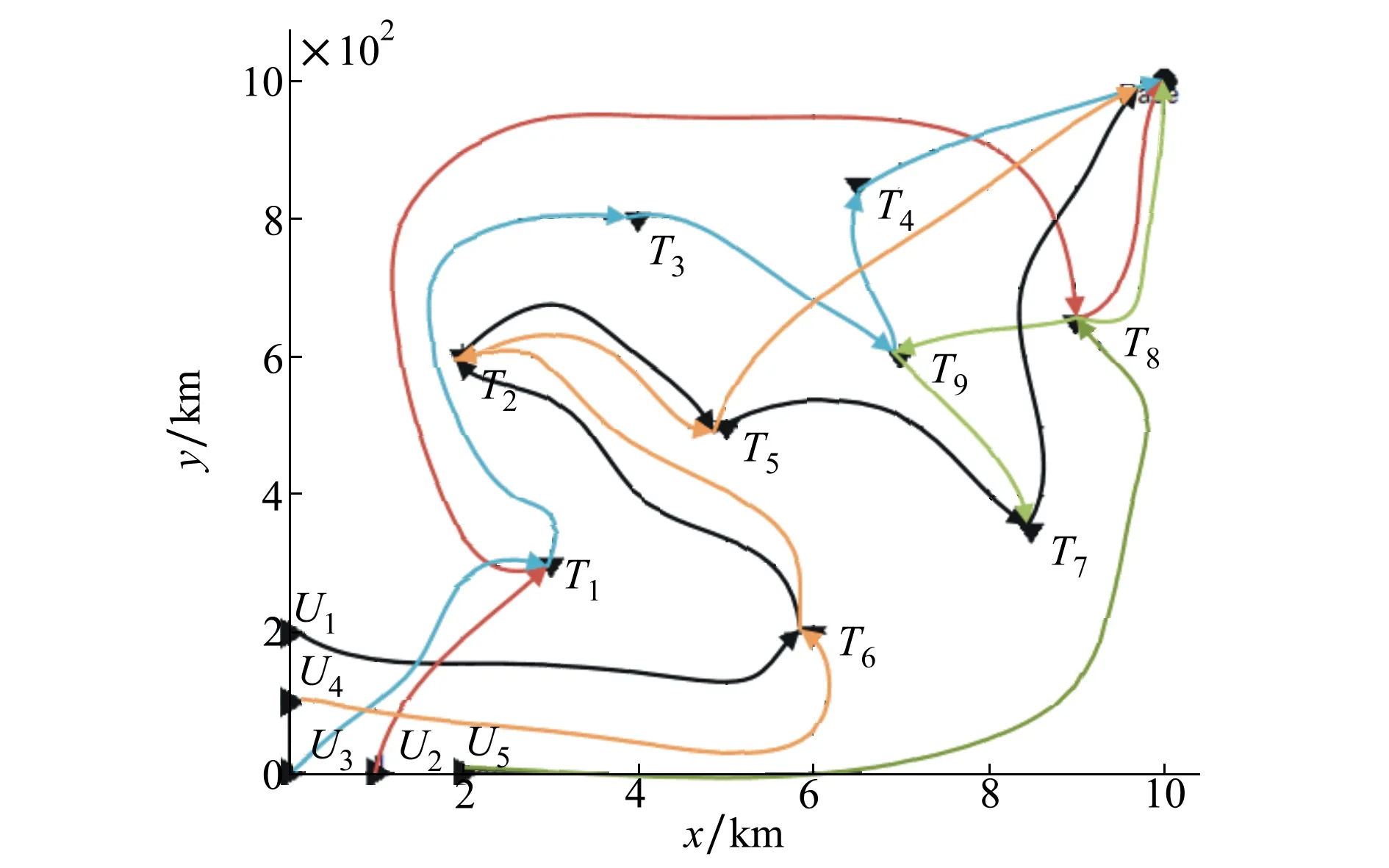
圖3 無人機執行任務過程示意圖

為了驗證GSA-GA算法的性能,針對上述問題,采用離散粒子群算法(DPSO)進行仿真對比分析,DPSO參數參照文獻[11]設置為:粒子種群規模為30,最大迭代次數為100,ω=0.5,c1=0.3,c2=0.2,圖4所示為2種算法求解下的收斂曲線。由圖中可以看出,相對于DPSO算法,改進的引力搜索算法能夠較快地收斂到最優解。但是由于2種算法均屬于啟發式優化算法,求得的結果往往不一定是最優解,也可能是次優解,因而單一的仿真結果并不能準確地比較出2種算法在求解任務分配問題上的優劣,針對以上問題分別采用2種算法進行200次蒙特卡羅法仿真實驗,2種算法的收斂過程如圖4所示,統計結果如表6所示。

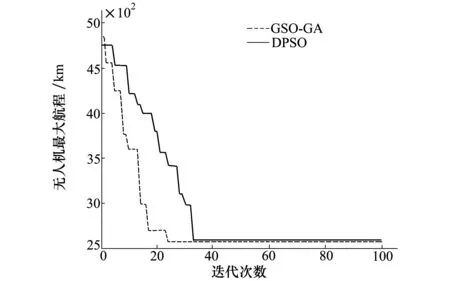
圖4 GSA-GA和DPSO的收斂曲線

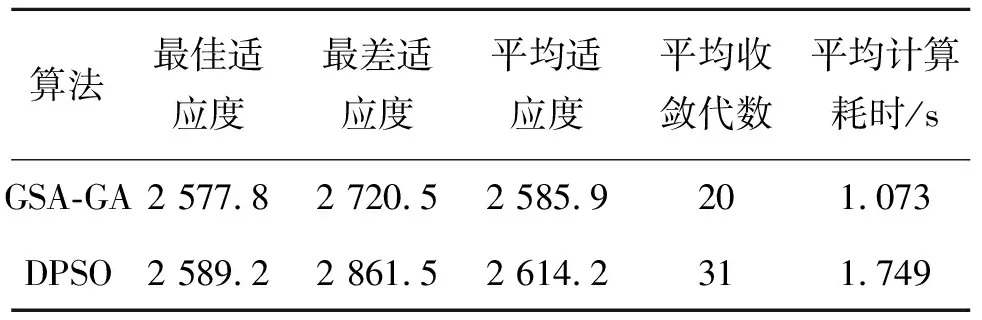
表6 GSA-GA與DPSO算法對比分析

如表6所示,經過200次隨機求解,改進的GSA-GA算法得到的最佳適應度為2 577.8,最差適應度為2 720.5,平均適應度為2 585.9 km,平均收斂代數為20代,平均消耗時間為1.073 s,相比于DPSO算法,在最佳適應度、平均收斂代數及平均消耗時間上均有更好的表現。實驗數據表明,改進的GSA-GA算法能夠更高效地對時序耦合約束下多UAV協同任務決策問題進行求解。

4 結 論

多無人機協同任務決策問題是一個十分復雜的典型NP-Hard問題,本文以多無人機協同執行SEAD任務為背景,重點關注任務間的時序耦合關系,對時序耦合約束下的多無人機任務分配問題進行了數學建模,提出了一種基于遺傳算子的混合引力遺傳搜索算法 (GSA-GA)并應用于任務分配問題的求解,通過算例仿真實驗驗證了所提出算法的有效性和合理性,并采用蒙特卡羅仿真方法對改進算法與離散粒子群算法進行了對比分析,結果表明GSA-GA 算法能夠更快地收斂,尋優結果更優。從而為無人機執行具有時序耦合約束任務時的協同任務分配問題提供了科學的決策依據。