基于多元可靠性模型的復雜結構件危險點選取方法

胡杰鑫,尹偉,任俊剛,孫維光,謝里陽

(1.東北大學航空動力裝備振動及控制教育部重點實驗室,110819,沈陽;2.北京強度環境研究所,100076,北京;3.中車青島四方機車車輛股份有限公司,266000,山東青島)

隨著科學技術的飛速發展,機械裝備趨于大型化和復雜化,并且要求的安全服役壽命也越來越長。對于絕大多數復雜結構件而言,在其服役周期內,主要的失效模式并不是靜強度失效,而是由交變載荷持續作用所導致的疲勞失效。因此,準確評估復雜結構件的疲勞壽命及可靠性,對于機械裝備的服役安全和改進升級至關重要。

在預測復雜結構件的疲勞壽命及可靠性時,主流方法都是先確定復雜結構件上的薄弱部位,作為復雜結構件的危險點,而后結合材料性能計算獲得危險點的疲勞壽命,即為復雜結構件的疲勞壽命。目前,多數學者在確定復雜結構件的危險點時,通常只是根據有限元分析的結果,選取應力集中或者應力最大的位置為危險點,利用此方法分析的復雜結構件包括高空作業平臺[1]、動車組車體[2]、列車枕梁[3-4]、隧道掘進機刀盤[5-6]、航空發動機燃燒室[7]、飛機蒙皮[8]、客車骨架[9]、鑿巖機活塞[10]、拖拉機車軸[11]等。復雜結構件危險點是否發生疲勞失效,不僅取決于應力集中或應力最大,還受到材料分散性、載荷作用次數、環境腐蝕等多種因素的綜合影響。以應力集中或者應力最大為判據確定的復雜結構件危險點有可能并不是真正的危險點,例如:在1個復雜結構件上,不同部位、不同材料的抗疲勞性能不同,如果高應力的位置處恰好材料的抗疲勞性能也高,其壽命并不一定比低應力且抗疲勞性能也低的位置壽命短,這在帶有焊縫的復雜結構件上表現得十分明顯。

為了獲得復雜結構件準確的疲勞壽命及可靠性評估結果,在確定危險點時需要綜合考慮各種影響因素,如載荷不確定性、材料性能不確定性、載荷作用次數和材料強度退化等。因此,本文提出了基于多元可靠性模型的復雜結構件危險點選取方法,并以某型號地鐵列車枕梁的疲勞可靠性評估為例,詳細展示了計算過程。

1 多元可靠性模型

復雜結構件的疲勞可靠性指的是其在規定的服役條件下,疲勞壽命大于設計服役時間的概率。若已知復雜結構件在復雜隨機載荷作用下的壽命分布,則其服役到t時刻的可靠性可以表示為

(1)

式中:h(τ)是復雜結構件在復雜隨機載荷作用下的壽命分布函數,但實際上很難獲得。

影響復雜結構件疲勞可靠性的因素有材料性能的不確定性、外界載荷的不確定性、規定時間內載荷的作用次數以及隨載荷作用而發生的材料強度退化。傳統的應力-強度干涉模型只考慮了強度和應力的不確定性,而且只適用于計算1次載荷作用下的可靠性。在傳統模型下,可靠性的計算公式為

(2)

式中:g(s)為應力概率密度函數;f(S)為強度概率密度函數。

隨著外界載荷作用次數的增加,理論上大載荷出現的次數會增多,因此復雜結構件的疲勞可靠性將隨之降低,故在式(2)的基礎上,考慮外界載荷作用次數對復雜結構件可靠性的影響,可靠性的計算公式可以表示為

(3)

式中:n為載荷作用次數,若n為隨機變量,且為時間t的函數時,則載荷作用次數的發生率可以表示為

P(N=n)=ωn(t)

(4)

其中,ωn(t)為載荷作用次數的概率分布函數。

復雜結構件安全服役到時刻t的可靠性為

(5)

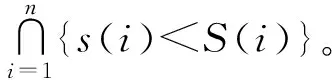
因此,在式(5)的基礎上,考慮材料強度退化的可靠性模型為

(6)

目前,許多學者對材料強度退化已經進行了深入研究,并根據不同的研究對象,提出了多種剩余強度模型,但普適性的模型還有待進一步研究。

式(2)～(6)所考慮的應力不確定性只是復雜結構件某一載荷歷程樣本內部載荷峰值導致的應力分布,但不同的載荷歷程對復雜結構件的可靠性影響也并不完全相同。因此,文獻[13]對外界載荷的不確定性做了進一步區分,定義了載荷宏觀不確定性(即載荷歷程具有不確定性)和載荷微觀不確定性(即同一載荷歷程樣本內部的載荷峰值具有不確定性)。在式(6)的基礎上,文獻[13]提出了綜合考慮載荷宏觀不確定性和微觀不確定性的多元可靠性模型

(7)

式中:h(L)為以L標識的宏觀載荷的概率密度函數;ωn(t,L)為以L標識的載荷歷程樣本的載荷作用次數的分布律;f(S)為強度概率密度函數;g(s,L)為以L標識的載荷歷程樣本的微觀載荷(應力)的概率密度函數;S(i)表示載荷第i次作用時的材料剩余強度,本文所采用的材料剩余強度S(i)的具體表達式詳見3.2節。

2 危險點選取思路

利用多元可靠性模型,可以全面地考慮載荷不確定性、材料性能不確定性、載荷作用次數和材料強度退化對復雜結構件危險點的疲勞壽命及可靠性的影響,據此提出的復雜結構件危險點選取方法的具體流程如圖1所示。其中,潛在危險點選取為有限元計算確定的復雜結構件的應力集中部位;多元可靠性模型以獲得的實際信息為基礎,如材料強度的概率密度函數、宏觀載荷的概率密度函數、微觀載荷的概率密度函數、載荷作用次數分布律以及剩余強度模型;危險點為在復雜結構件的設計服役年限內,對其疲勞可靠性構成較大影響的點,即危險點的可靠性小于0.999 9。

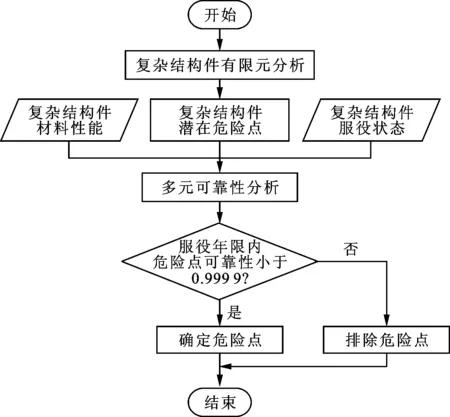
圖1 復雜結構件危險點選取流程圖

3 地鐵列車枕梁危險點選取實例

以某型號未投入使用的地鐵列車枕梁為例,利用本文提出的危險點選取方法,具體展示地鐵列車枕梁危險點的選取及計算過程如下。

3.1 載荷不確定性

載荷不確定性包括載荷的宏觀不確定性和微觀不確定性。對于地鐵列車枕梁而言:載荷宏觀不確定性表現為同一型號的地鐵列車在不同軌道運行的不確定性,由于不同的地鐵軌道所處的地理位置不同,并且不同城市的地鐵乘客數也存在很大差異,因此即使是同一輛列車在不同軌道上運行,所受到的載荷也存在明顯的不確定性;載荷微觀不確定性表現為地鐵列車枕梁在同一線路上運行時所受載荷的不確定性,雖然列車運行在固定不變的軌道上,但每天的人流量并不完全相同,因此在地鐵列車枕梁上的載荷也存在差異。

獲得載荷不確定性的最好方法是統計同一型號列車的銷售和使用情況,并對運行在不同軌道的地鐵列車枕梁進行疲勞載荷實測。宏觀載荷的概率分布根據在不同軌道上運行的同一型號列車的數量來確定,某一軌道的微觀載荷概率分布則通過對該線路枕梁所受的疲勞載荷的實測結果來統計獲得。由于該型號地鐵列車枕梁并未投入使用,而且不同線路上地鐵列車枕梁的應力實測數據也無法獲得,因此,根據相關國際標準[14-18],同時參照沈陽地鐵1號線的運營情況,利用泊松隨機過程編制合理的地鐵列車枕梁載荷譜。

地鐵列車在運行過程中,枕梁將承受中心銷載荷和空氣彈簧載荷,而它們均為整車質量的函數。地鐵列車整車質量由車身質量和乘客質量構成,設計載客量為226人、允許超員至290人的地鐵列車,假設每位乘客體重為60 kg,則乘客質量的正常變化范圍為0～13.56 t,約占車身質量20.5 t的1/2。根據《鐵道車輛車體結構靜載荷試驗方法》[17]和《鐵路機車車輛客車結構體設計一般要求》[18]的規定:在疲勞載荷未知的情況下可以將乘客數量變化作為載荷變化的來源。因此,在地鐵列車枕梁算例中,將乘客質量變化作為引起疲勞載荷變化的主要因素。

泊松隨機過程是一類較為簡單的時間連續且狀態離散的隨機過程。地鐵乘客數量每天都是從0開始,每站之間乘客增加數量相互獨立,同時乘客數量增加是獨立增量過程。因此,地鐵乘客數量變化是一個泊松隨機過程[19],且參數表示單位時間內到達地鐵車站候車的平均乘客數量。某時刻沈陽地鐵1號線各站乘客數見圖2。

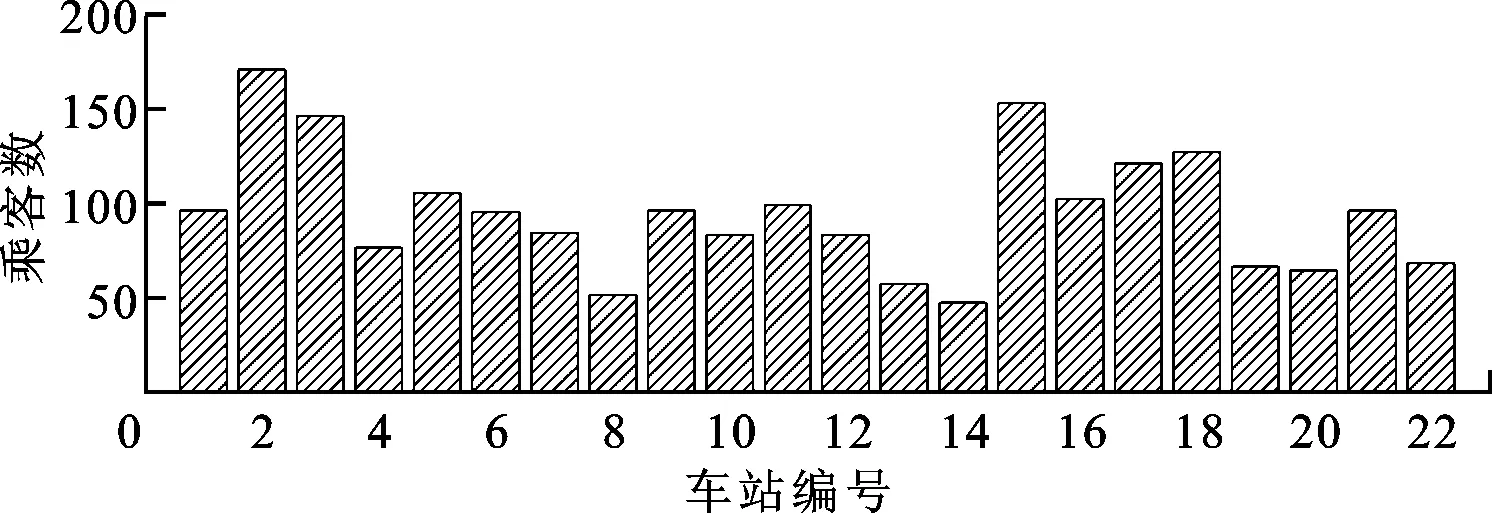
圖2 某時刻沈陽地鐵1號線各站乘客數

沈陽地鐵1號線共22站,每天運行18趟,乘客數量變化396次。假設該地鐵列車枕梁將會服役于國內10個城市的地鐵線路,每天的乘客數量變化次數即為地鐵線路車站數與每天運行數量的乘積,每站乘客的候車數可利用泊松隨機過程來模擬,其參數與城市乘坐地鐵的人口數相關。利用上述方法,產生了10種不同的乘客數量變化譜,作為該地鐵未來服務于10個不同城市將會受到的模擬載荷譜,匯總的信息如表1所示。

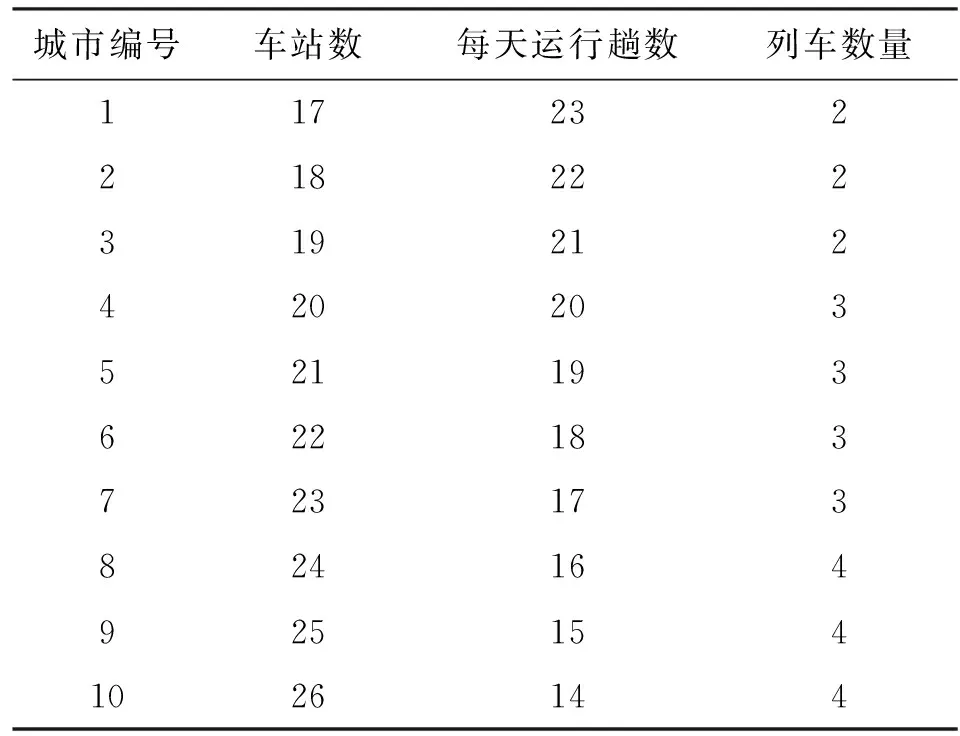
表1 10個城市地鐵的模擬載荷譜

對某城市100天的乘客數量進行觀察,取每天乘客數量的最大值統計獲得的概率分布即為該城市地鐵列車枕梁微觀載荷的概率分布。泊松隨機過程模擬產生并統計獲得的10個城市的微觀載荷概率分布如表2所示,而地鐵列車枕梁在該市的宏觀載荷概率為該市地鐵線路上運行的列車數量占該型號列車總數的比例,每個城市的具體列車數量見表1。

地鐵列車枕梁危險點的微觀載荷(應力)與乘客數量之間的關系可以根據枕梁的理論載荷公式和有限元方法計算獲得,在此不再贅述。

3.2 強度分布及退化模型

地鐵列車枕梁結構件含有鋁合金板材、型材和焊縫,雖然有限元分析結果顯示最大應力主要出現在鋁合金型材上,但由于其強度較高且抗疲勞性能較好,一般不會發生疲勞失效,因此本例以角焊縫為主要研究對象,選擇的潛在危險點(應力集中部位)均位于角焊縫處。根據文獻[20]對鋁合金焊縫抗疲勞性能的研究,鋁合金角焊縫的強度極限服從均值為193.25、標準差為9.61的正態分布。

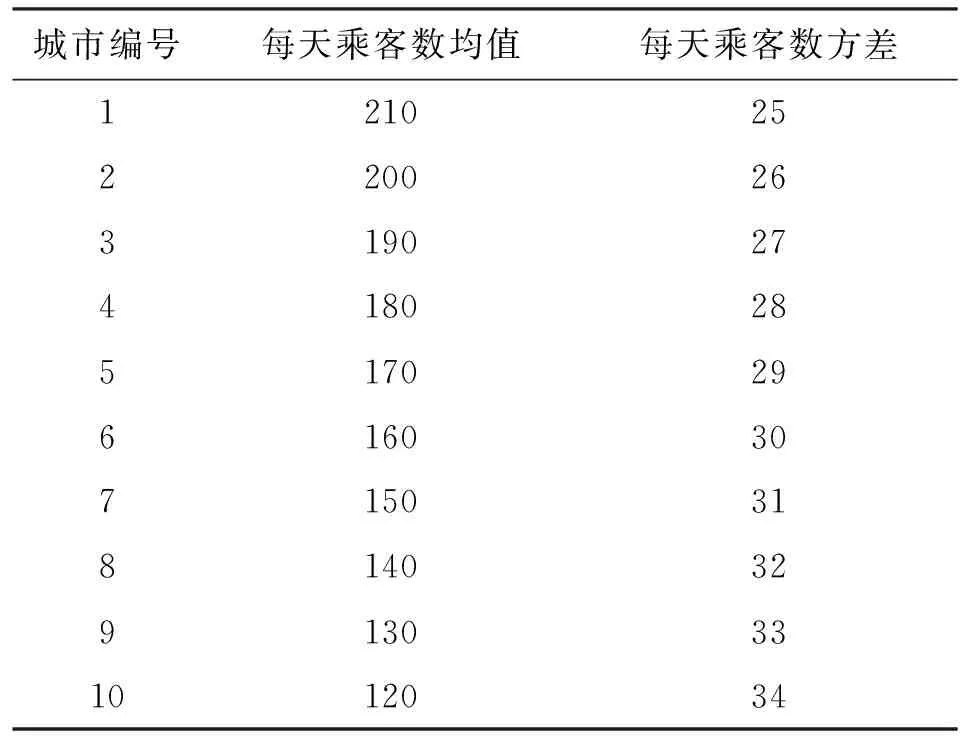
表2 10個城市地鐵的微觀載荷概率分布

隨著地鐵列車枕梁服役時間和載荷作用次數的增加,角焊縫的材料性能逐漸退化,剩余強度將會按某種規律降低,當低于所承受的正常工作應力時即發生疲勞失效。現假設本算例中角焊縫的剩余強度與載荷的作用次數為對數關系,具體表達式[13]為

(8)

式中:S(n)為應力作用n次后的剩余強度;S0為材料的初始強度;σmax為循環應力最大值;n為應力作用次數;Nf為σmax應力水平下的疲勞壽命。

由于式(8)只是一個非線性強度退化模型,而實際使用情況更加復雜。考慮到在復雜載荷歷程作用下(如地鐵列車乘客數量復雜多變),疲勞損傷的非線性效應有很大一部分將會相互抵消,并且有些材料及結構的剩余強度本身就是近似地按線性規律退化,因此,可將式(8)的非線性模型進行初級近似,用線性退化模型描述復雜載荷歷程下的強度退化規律,表達式[21]為

S(n)=S0+(S0-σmax)[n/(N-1)]

(9)

當n=0時表示材料的初始狀態,此時S=S0,S0為靜拉伸強度極限;當n=N-1時(N為疲勞壽命),表示剩余強度已經達到了臨界破壞狀態,此時S=σmax,當應力比為-1時,σmax與應力幅σa相等。在本算例中,角焊縫的初始強度取為193.25 MPa,循環應力最大值為乘客滿員時危險點處壽命為107次載荷循環時所對應的應力值。

由于地鐵列車枕梁不同部位的應力比并不相同,在循環載荷作用下,即使是同種材料,其退化規律也會有差異,這主要是因為危險點處單位載荷循環所造成的疲勞損傷受平均應力影響。因此,在確定式(9)中的σmax時,需要考慮應力比(或者平均應力)的影響。通過研究平均應力對角焊縫處疲勞極限的影響,發現Goodman壽命直線的等效結果最準確[20]。Goodman壽命直線方程為

(10)

式中:σa為應力幅;σ-1為應力比為-1時的疲勞極限;σm為平均應力;σb為強度極限。

利用式(10)計算確定的潛在危險點壽命為107次載荷循環時的σ-1,即為該點在式(9)中的σmax。

3.3 載荷作用次數

本算例中造成角焊縫強度退化的載荷是在每天乘客較多時產生的,這樣的載荷每天出現的概率服從泊松分布,其參數的含義為每天地鐵列車枕梁大載荷出現次數的期望值。對于某一條確定的地鐵線路,由于城市的發展,該線路上每天大載荷出現的次數會隨著時間的推移而發生變化,但在此并不做考慮,僅假設大載荷每天出現次數的概率固定不變,載荷作用次數的分布律為

(11)

10個城市地鐵的載荷作用次數見表3。

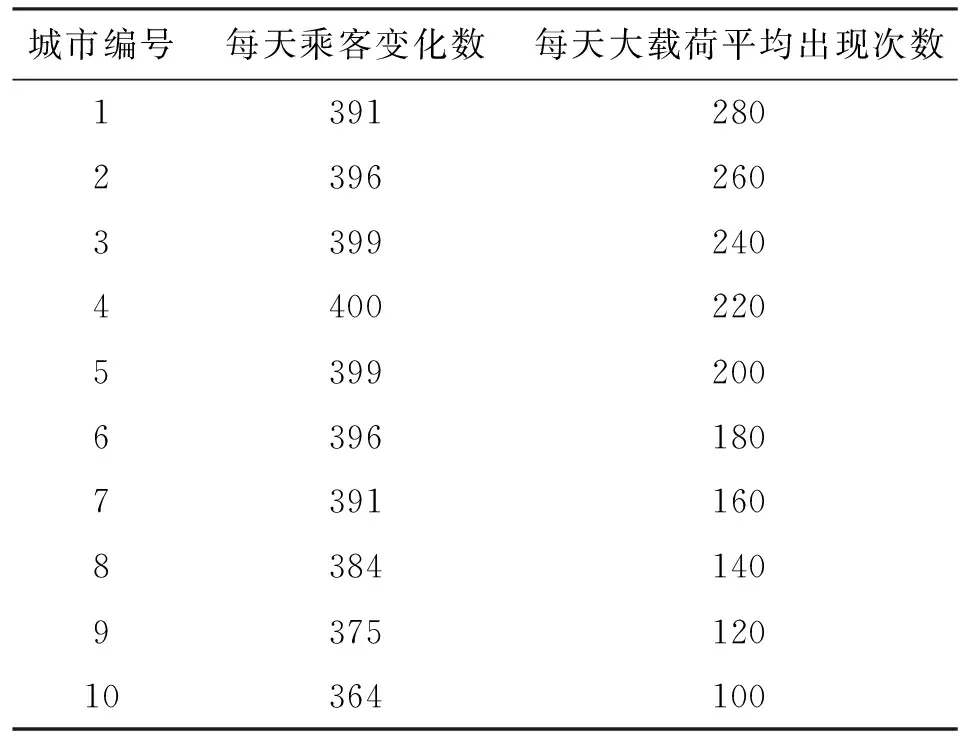
表3 10個城市地鐵的載荷作用次數

3.4 列車枕梁潛在危險點

按照相關標準[14-18]對該地鐵列車枕梁進行有限元分析,有限元計算模型如圖3所示。其中,在最大載荷工況時,根據標準設計的中心銷載荷為50 kN,空氣彈簧載荷為110.57 kN。

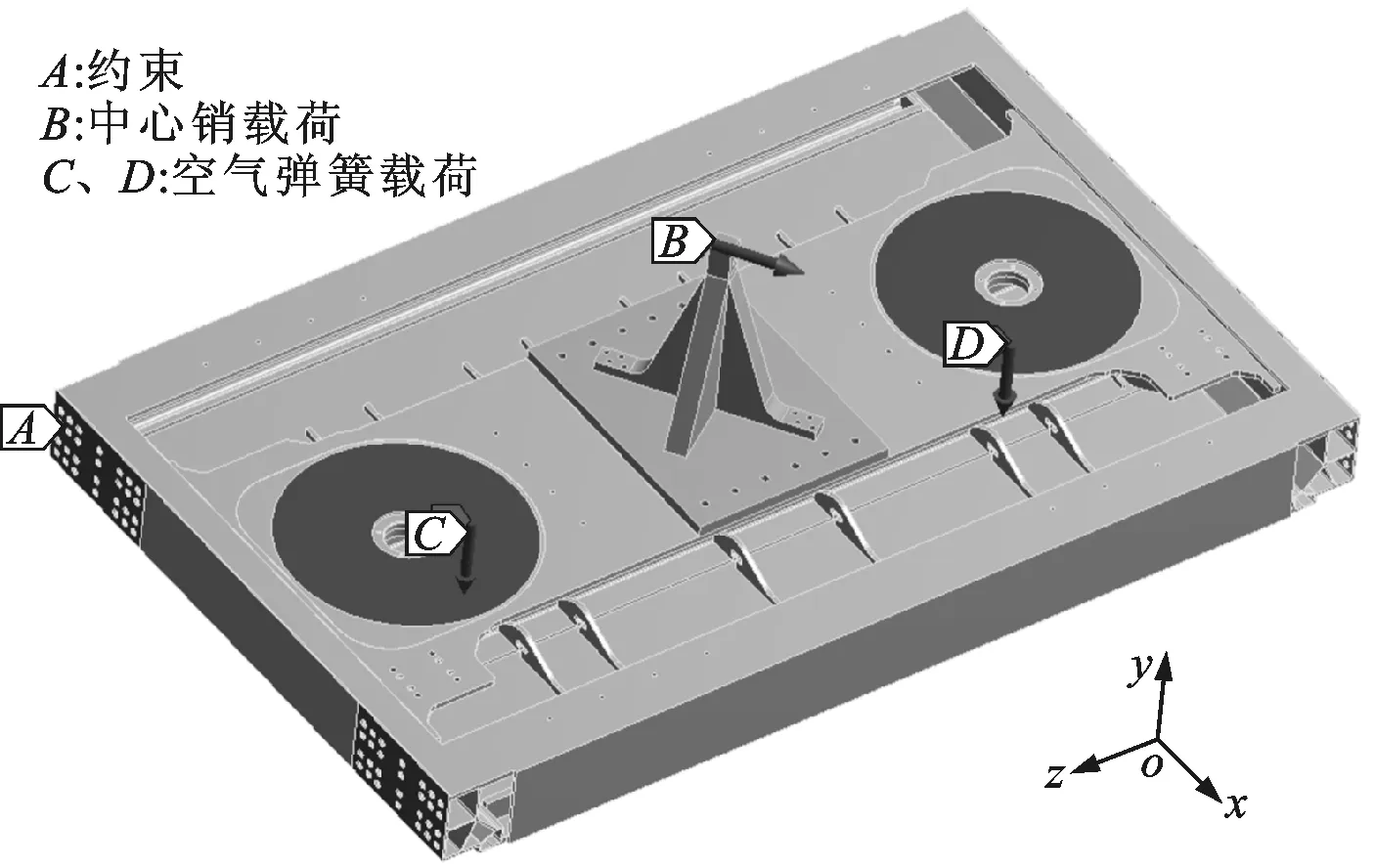
圖3 列車枕梁有限元計算模型

根據有限元分析結果,從角焊縫處選取28個應力集中位置,并根據角焊縫p-S-N曲線[20],利用Gerber壽命圖[12],對這些位置的疲勞壽命進行了評估,結果如圖4所示。

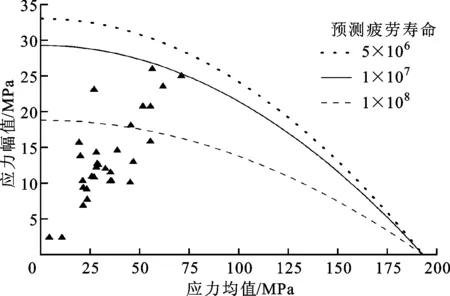
圖4 存活率為99%時列車枕梁的Gerber壽命圖

這28個應力集中位置均為地鐵列車枕梁的潛在危險點,但本算例僅選取壽命較短的7個點(圖4中預測疲勞壽命介于107和108次載荷循環之間)來討論,具體位置如圖5所示,其應力狀態如表4所示。

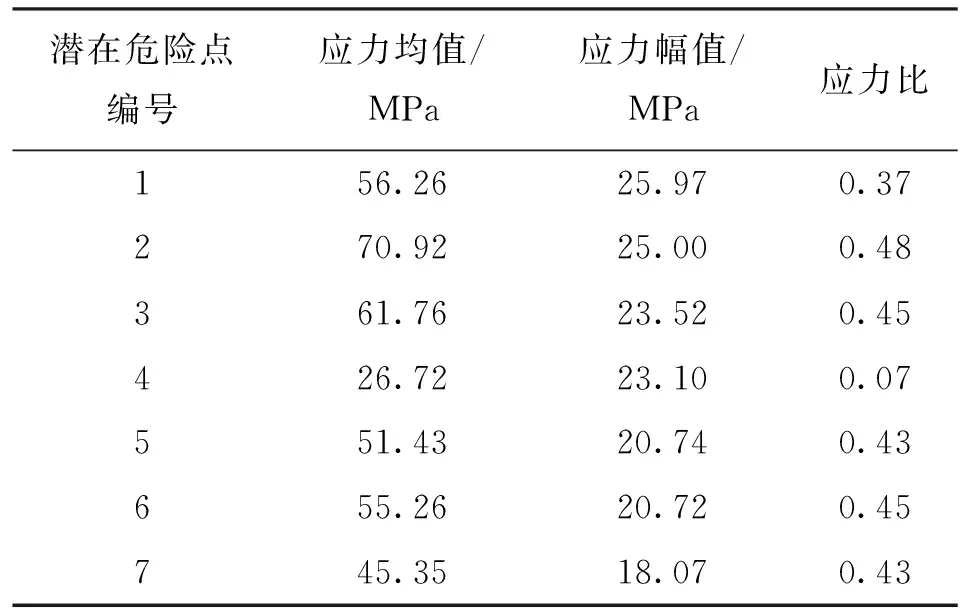
表4 潛在危險點應力狀態

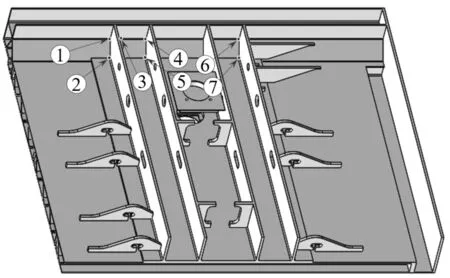
圖5 列車枕梁7個潛在危險點的位置

3.5 列車枕梁可靠性

根據前文的分析與假設,本算例中危險點的多元可靠性模型為

(12)

式中:t為時間,單位為d,每年以365 d計算;l為城市編號;P(L=l)為城市l的宏觀載荷概率;P(N=n)為載荷出現n次的概率;f(S)為強度概率密度函數;S((t-1)N(l)+i)為在城市l上運行第t天時的剩余強度;gl(s)為城市l的微觀載荷概率密度函數。將相關參數代入式(12),分別計算地鐵列車枕梁7個潛在危險點的可靠性,結果如圖6所示,可以看出:當服役時間達到60 a時,點1的可靠性開始下降,點2和點3的可靠性分別在服役64 a和68 a出現下降,其余4點的可靠性始終約為1。

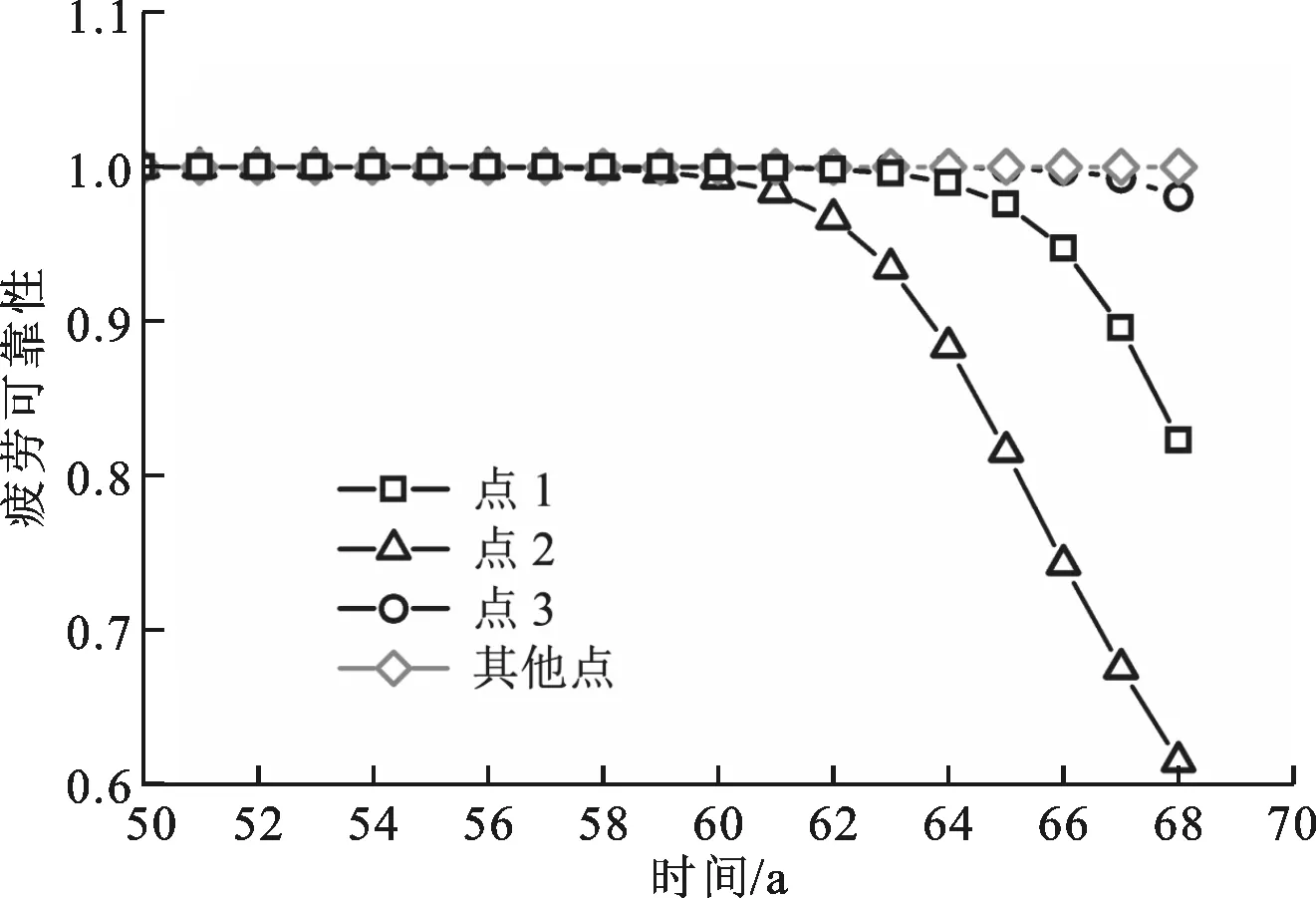
圖6 潛在危險點的疲勞可靠性

根據圖6中潛在危險點的疲勞可靠性信息,可假設該地鐵列車枕梁是由x個潛在危險點構成的串聯系統,據此來計算枕梁的疲勞可靠性,結果如圖7所示。分析可知,潛在危險點1、2對地鐵列車枕梁疲勞可靠性的影響較大,是地鐵列車枕梁的真正危險點,而其他潛在危險點對枕梁疲勞可靠性的影響較小且可以忽略。同時,該地鐵列車枕梁在假設的服役環境中,完全滿足安全服役30 a的設計要求,并且服役60 a的累計失效概率僅為0.75%。

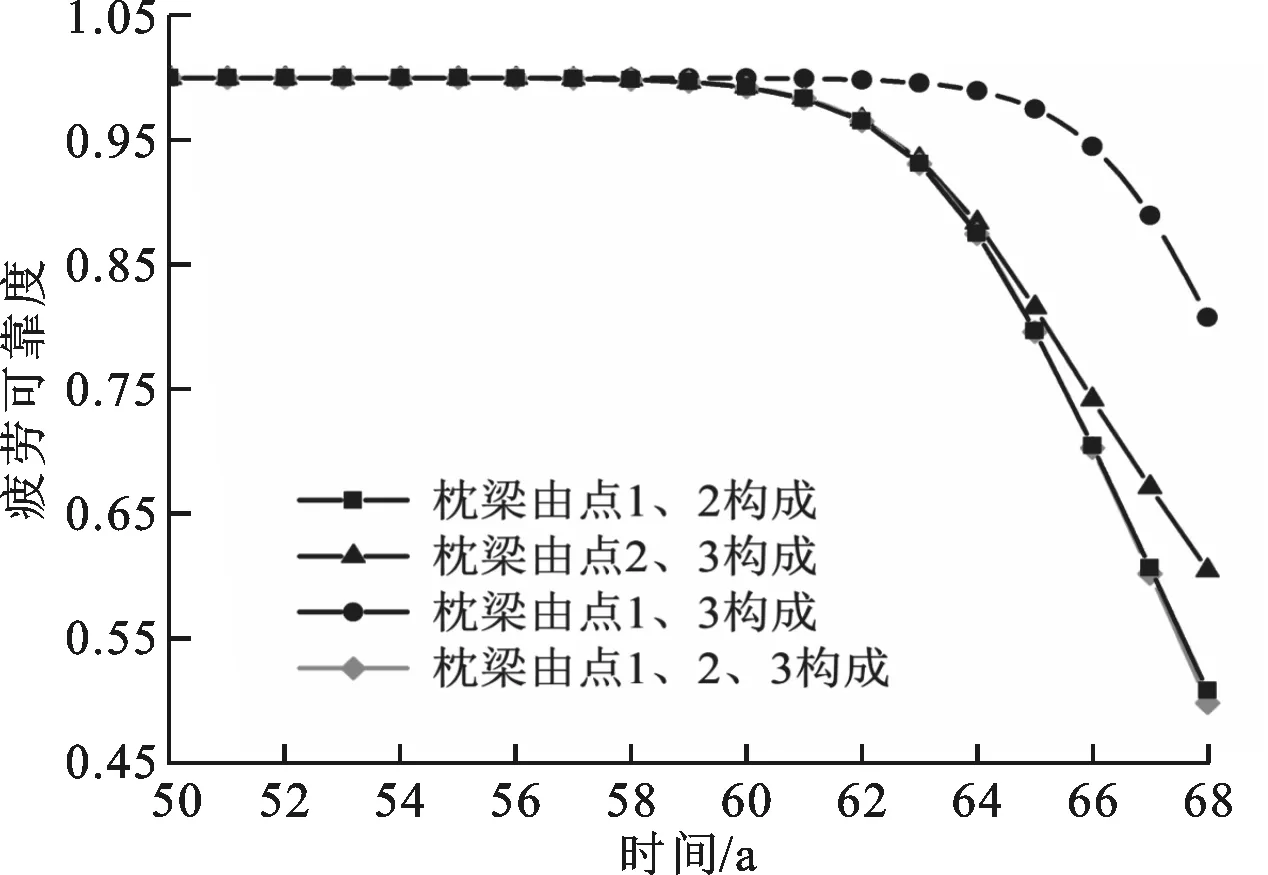
圖7 地鐵列車枕梁的疲勞可靠性

本算例只是對位于角焊縫處的危險點進行可靠性評估和選取,當復雜結構件上同時存在多種材料,并且應力分布很不均勻的時候,利用多元可靠性模型的危險點選取方法較傳統的、僅僅以應力集中或者應力最大為依據的危險點選取方法具有更加明顯的優勢,且復雜結構件的疲勞壽命及可靠性評估結果也更加準確。

4 結 論

(1)從傳統的應力-強度干涉模型出發,討論了載荷作用次數、強度退化、載荷不確定性和強度不確定性等因素對復雜結構件疲勞可靠性的影響,建立了相應的多元可靠性模型,據此提出了用于評估復雜結構件疲勞壽命及可靠性的危險點選取方法。

(2)以某型號地鐵列車枕梁為例,詳細展示了基于多元可靠性模型的危險點選取過程。其中,根據地鐵列車相關標準,并參照沈陽地鐵1號線的運營情況,利用泊松隨機過程編制了該地鐵列車枕梁未來將服役的10條線路載荷譜,同時假設了載荷宏觀不確定性和微觀不確定性的相關參數。

(3)以應力集中為依據確定的28個潛在危險點中,經分析只有2個危險點對該地鐵列車枕梁疲勞可靠性會產生較大影響。同時,枕梁在假設的服役環境中運行60 a的可靠性約為99.25%,完全滿足設計要求。