基于代理模型的麥克風相位陣列設計技術研究

丁存偉, 李周復, 張 雪, 周國成

(中國航空工業空氣動力研究院, 哈爾濱 150001)

0 引 言

麥克風相位陣列測量技術的應用[1-5]，使得聲學風洞試驗能夠對試驗模型的主要噪聲源進行定位，獲取聲源強度、頻率等豐富的聲學特性信息，成為當前飛行器聲學試驗研究中不可或缺的測量手段。

麥克風相位陣列測量性能主要通過陣列分辨率(Resolution)和最大旁瓣水平(Maximum Sidelobe Level, MSL)進行衡量。陣列分辨率和最大旁瓣水平會隨著目標聲源頻率的改變而發生明顯變化。同一期聲學風洞試驗中模型構型、來流風速等試驗狀態的不同，可能導致主要聲源位置、尺寸和噪聲頻率的顯著改變，對麥克風陣列分辨率和最大旁瓣水平的需求也隨之變化，從而超出了原有陣列的最佳適用范圍，導致某些狀態下測量結果的精準度受到影響。為了實現最佳測量效果，麥克風相位陣列也應針對聲源特性的變化而實時改進，但是，這一改進過程必須滿足風洞試驗對現場操作的高效率要求。目前聲學試驗中普遍采用格柵式快速插拔陣列支架，能夠支持麥克風陣列的快速拆裝，因此，需要解決的問題是：根據試驗狀態對陣列分辨率和最大旁瓣水平的需求，如何在較短的時間內完成麥克風相位陣列的優化設計。

在麥克風相位陣列設計方面，國內外研究人員研究了陣列尺寸和麥克風布置方式等因素對陣列分辨率和最大旁瓣水平的影響，并且將粒子群算法、模擬退火法等優化設計方法引入了麥克風陣列設計中[4,6-13]。但是以上研究方法并未考慮陣列設計的耗時問題。盡管陣列設計中通常采用計算量較小的點擴散函數進行陣列性能分析，但是當聲源定位面內掃描點數較多，優化搜索空間較大時，計算量將會顯著增加，完成整個陣列優化工作可能需要耗時數小時至數十個小時不等。這種計算耗時無法滿足風洞試驗過程中及時改進麥克風陣列的應用需求，必須研究更加高效的麥克風相位陣列設計方法。

基于Kriging模型的優化方法很好地解決了計算量與計算精度的問題，顯著提升了優化效率，已經在飛行器氣動設計領域得到了大量的應用[14-21]。文獻[14]開展了旋翼槳尖氣動與噪聲綜合優化設計研究，其中旋翼的氣動性能和噪聲特性需要應用非定常流場求解方法進行計算，單點計算耗時較高。如優化過程中全部采用非定常方法進行目標函數計算，則其計算量將急劇增加，無法滿足工程應用需求。文章采用Kriging模型代替復雜費時的非定常計算，采用遺傳算法進行優化，有效解決了計算耗時問題，建立了一種工程實用的旋翼槳尖優化設計方法。此外，為了解決計算量過大的問題，文獻[15]應用Kriging模型進行了機翼氣動/結構剛度耦合優化設計，文獻[16]將Kriging模型應用于高升力翼型的優化設計研究。可見，Kriging模型的應用是提升優化效率的有效方法。

為了最大限度提升麥克風相位陣列設計效率，本文借鑒飛行器氣動優化設計領域的研究方法，創新性地將Kriging代理模型方法引入陣列優化設計研究中。采用點擴散函數進行樣本點性能分析，建立Kriging模型，應用遺傳算法進行優化，形成了一種效率極高的麥克風陣列設計方法。該方法可有效改善陣列對目標聲源的測量性能，滿足聲學風洞試驗中針對特定聲源及時改進麥克風相位陣列的需求，有助于改善試驗測量精準度，提升試驗效率。

1 基于代理模型的陣列優化設計方法

1.1 陣列性能分析方法

陣列性能分析是通過給定模擬點聲源，計算陣列對該聲源激勵的波束形成響應來評估陣列性能的一種技術手段。陣列設計過程中，進行陣列性能量化分析時，波束形成響應通常表示為點擴散函數(Point Spread Function, PSF)[22]。采用基于點擴散函數的計算方法分析陣列對模擬聲源的定位效果，是陣列設計過程中較為常用且可靠的性能分析方法，可以定量地評價麥克風陣列定位性能。計算方法如下：

陣列測量位于yj處的單位聲源，獲得互譜矩陣(Cross Spectrum Matrix, CSM)：

(1)

(2)

則位于yj的單位聲源在掃描點k處的波束形成輸出可表示為：

(3)

上式為PSF的定義式，Wk為對應麥克風的權向量，是關于引導向量g的函數，取決于麥克風陣列與掃描平面的位置、測量環境與聲源頻率。

采用點擴散函數完成全部掃描點上的波束形成輸出計算后，陣列性能分析結果通常以聲壓級云圖的形式給出，從中可以獲取陣列分辨率和最大旁瓣水平兩個主要性能參數。其中，陣列分辨率描述了陣列定位聲源和分辨臨近聲源的能力；陣列的最大旁瓣水平表明陣列放大目標聲源、抑制背景噪聲的能力。

1.2 設計變量與約束條件

與其他陣列形式相比，多臂螺旋陣列能夠在較寬的頻率范圍內保持良好的旁瓣抑制性能，因此在聲學試驗中得到了廣泛應用，本文主要針對這種陣列進行優化設計舉例。已有的多臂螺旋陣列設計方法中，螺旋線上麥克風的位置主要采用等弧長分布，或者等環形區域面積分布的方式確定[22]，無需進行優化計算，但是設計空間較為單一。本文將多臂螺旋陣列的螺旋線軌跡、麥克風分布位置、旋臂數等信息進行參數化，拓展了陣列設計空間，通過對設計參數的優化，搜索得到性能優良的陣列方案。多臂螺旋陣列設計參數包括：懸臂數目n，螺旋線系數a和k，麥克風沿螺旋線分布參數q。

對數螺旋線可用極坐標表示如下：

r=a·ekθ

(4)

其中，r為極徑，θ為極角，a、k為常系數。

當系數a、k確定之后，螺旋線的軌跡即為確定值。麥克風在螺旋線上的分布通過參數q進行確定，具體方法如下：

相鄰兩麥克風間螺旋線弧長成等比增長，比值為q。對于最大極徑為R的對數螺旋線，當q=1時，螺旋線上麥克風為均勻分布；q≠1時，第m個麥克風的極坐標為：

(5)

(6)

其中，j為單條懸臂上麥克風數量，由整個陣列可用的麥克風總數和懸臂條數決定。

對于有n條旋臂的螺旋陣列，將陣列面板按2π/n弧度等分為n份，并通過麥克風坐標點的旋轉復制得到整個陣列坐標。

試驗環境、設備以及試驗對象等因素決定了麥克風陣列設計需要考慮的約束條件。試驗場地的空間限制和聲源定位范圍約束了陣列最大直徑；試驗中可供使用的麥克風總數量決定了陣列單元數；麥克風尺寸和安裝方式決定了兩麥克風最小間距。因此，優化過程中的約束條件包括：陣列直徑、麥克風數量、麥克風最小間距。

1.3 基于Kriging模型的遺傳算法

遺傳算法不僅具有全局性優化的特點，而且具有良好的魯棒性、可靠性和移植性，在工程優化設計領域應用較為廣泛。但是遺傳算法通常需要的種群規模龐大，容易導致計算量過大。本文采用基于Kriging模型的遺傳算法開展陣列優化設計。Kriging模型在保證陣列性能預測精度的同時，極大地提升了優化效率，同時使遺傳算法的種群規模不再受到計算量的限制，有效拓展了優化搜索空間。

Kriging代理模型是一種插值模型，由一個參數模型和一個非參數隨機過程構成，通過選擇適當的優化算法計算得到模型參數最優值，進而建立Kriging模型[18-19]。圖1給出了基于代理模型的陣列優化方法流程圖。其基本思想為：

(1) 采用試驗設計方法生成設計空間內的樣本點；

(2) 通過陣列性能分析程序計算樣本點的響應值；

(3) 由樣本信息及其響應值構建代理模型；

(4) 采用遺傳算法進行優化，種群適應度計算由代理模型完成；

(5) 按照選定的加點方法，搜索性能更優的樣本點；

(6) 采用陣列性能分析程序對最優樣本點進行分析；

(7) 判斷是否達到設計目標，若是，則輸出結果，停止優化；若否，則對原樣本集進行更新，以建立更加精確的代理模型，返回步驟(3)，重復優化過程直至滿足停止條件。

圖1 優化設計方法流程圖

2 麥克風陣列優化設計算例

針對分辨率和最大旁瓣水平兩個指標分別進行陣列優化，以驗證該優化設計方法的實用性。當分辨率為目標函數時，設置滿足試驗測量要求的最大旁瓣水平下限指標作為約束條件；以最大旁瓣水平為目標函數時，則給定分辨率指標作為約束。

2.1 多臂螺旋陣列分辨率優化

針對1m直徑量級63通道多臂螺旋陣列進行優化設計，優化問題總結如下：

設計狀態：2kHz單極子模擬聲源，定位區域1m×1m；

目標函數：分辨率最小，最大旁瓣水平≤-14dB；

設計變量：懸臂數目n，螺旋線系數a，k，分布參數q；

設計約束：陣列直徑D=1m，麥克風最小間距dmin≥0.02m，麥克風總數Nm=63。

共調用60次陣列性能分析程序進行樣本點計算，建立了代理模型。表1給出了Kriging代理模型的預測結果與數值模擬分析結果對比，代理模型預測誤差小于1%，預測精度完全滿足優化設計需求。遺傳算法優化過程中，以代理模型進行種群適應度計算，種群規模為200，交叉概率0.8，變異概率0.05，共進行了100代遺傳優化。優化程序采用單核運行，整個優化過程耗時約10min，獲得了性能較優異的陣列方案。可見，Kriging代理模型的應用顯著減少了計算時間，極大地拓展了優化搜索的范圍。

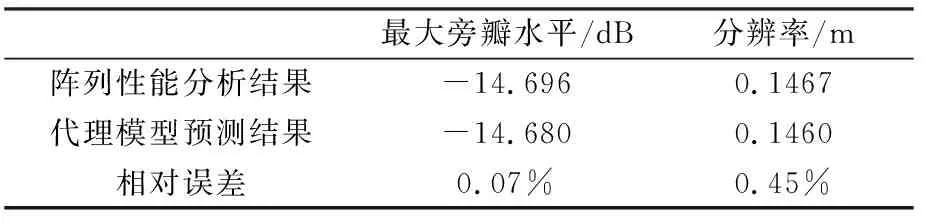
表1 Kriging模型預測誤差Table 1 Prediction error of Kriging model

取每個設計變量上、下限的平均值為初始陣列，作為設計參考，優化前后設計變量取值如表2所示。優化前后陣列單元分布情況如圖2所示，可見優化后陣列從中心向邊緣方向，單條螺旋線上麥克風間距逐漸減小，陣列單元的分布有向陣列邊緣移動的趨勢。圖3給出了2kHz模擬聲源下陣列響應云圖，可見優化陣列的分辨率有明顯改善。

表2 分辨率優化陣列設計變量Table 2 Design variables of resolution optimized array

(a) 初始陣列

(b) 分辨率優化陣列

Fig.2Schematicofinitialarrayandresolutionoptimizedmulti-armspiralmicrophonearray

與全尺寸飛機相比，航空聲學風洞試驗中的試驗模型通常是經過大幅縮比的，主要噪聲的頻率被相應放大。因此，本文主要進行1～6kHz頻率范圍內麥克風陣列測量性能分析，能夠滿足航空聲學風洞試驗的大部分測量需求。表3給出了優化后陣列與初始陣列性能對比數據，在1～6kHz頻率范圍內，優化陣列的分辨率均優于初始陣列，以設計點2kHz頻率性能為例，優化陣列分辨率從0.187m改善為0.164m，旁瓣聲壓級(SPL)略有升高，但最大旁瓣水平(MSL)滿足-14dB的約束要求。

(a) 初始陣列結果

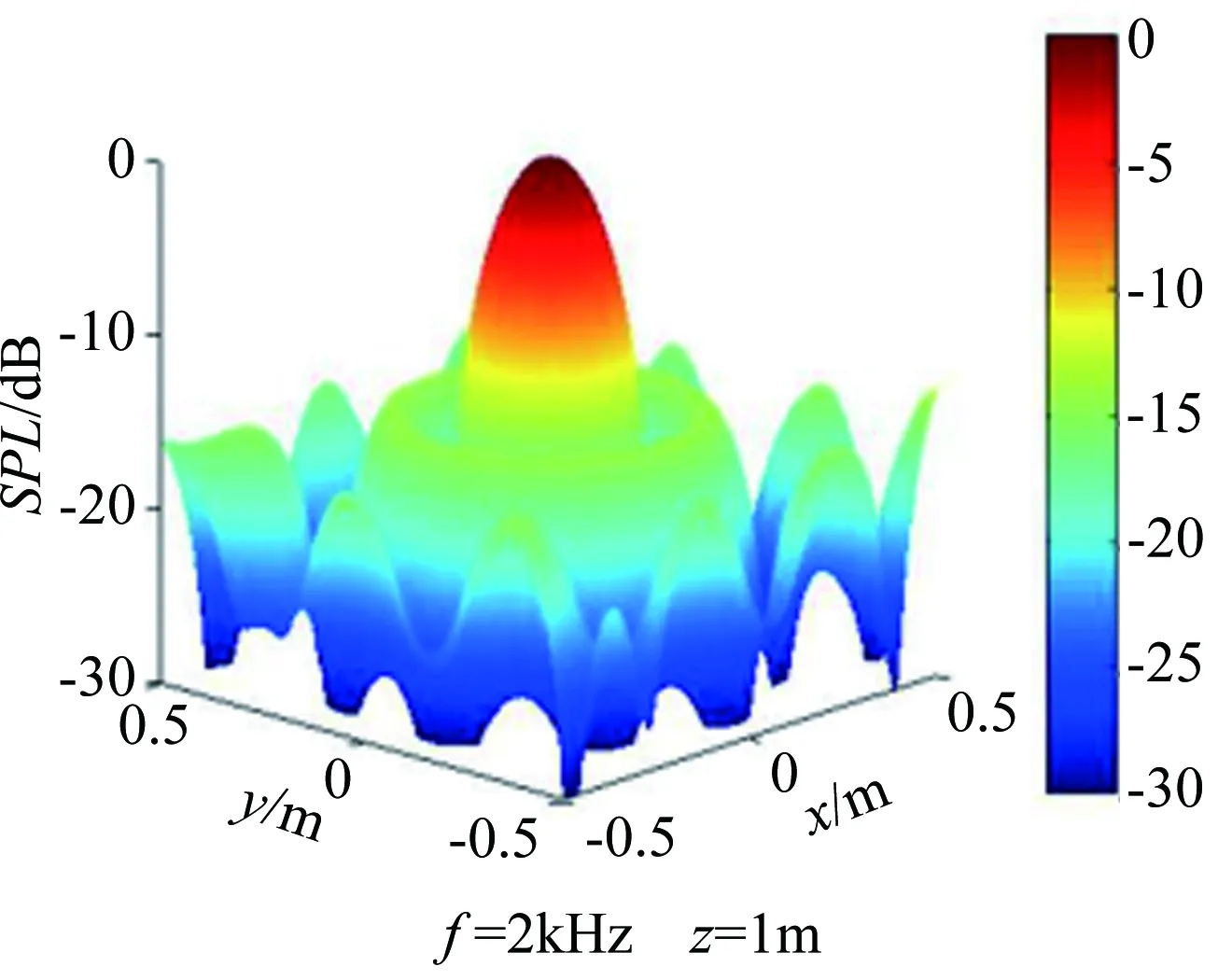
(b) 分辨率優化陣列結果

Fig.3Responsesofinitialarrayandresolutionoptimizedmicrophonearray

表3 初始陣列與分辨率優化麥克風陣列性能Table 3 Performance of initial array and resolution optimized microphone array

2.2 多臂螺旋陣列最大旁瓣水平優化

麥克風陣列最大旁瓣水平優化算例的設計狀態、設計變量、設計約束等均保持不變，目標函數變化為：最大旁瓣水平降低、分辨率≤0.2m。

優化后陣列單元分布如圖4所示，可見優化后陣列單元向中心區域集中。圖5給出了2kHz模擬聲源下的陣列響應云圖，可見優化陣列的最大旁瓣水平有明顯改善。表4給出了優化后陣列與初始陣列性能對比數據，可以看出在1～6kHz頻率范圍內，優化陣列的最大旁瓣水平明顯優于初始陣列，以設計點2kHz頻率下性能為例，優化陣列最大旁瓣水平有5dB的改善，分辨率滿足0.2m的優化約束條件。

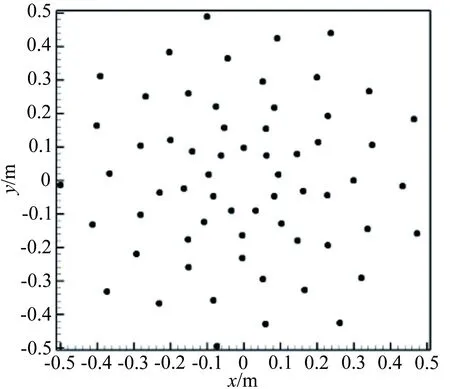
圖4 最大旁瓣水平優化陣列示意圖

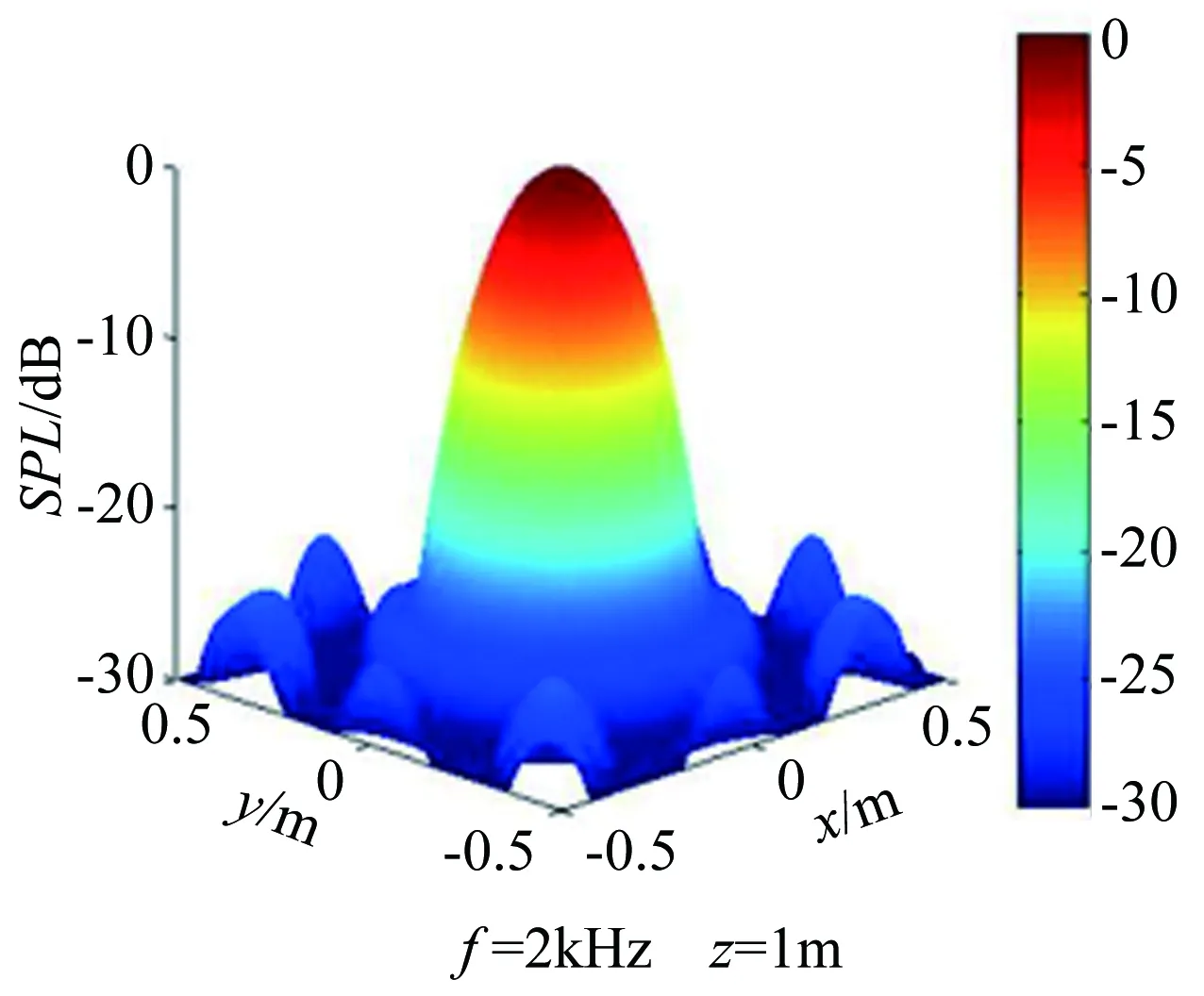
圖5 最大旁瓣水平優化陣列響應圖

初始陣列優化陣列頻率/kHz最大旁瓣水平/dB分辨率/m最大旁瓣水平/dB分辨率/m1-17.4120.388-20.5370.4122-16.8820.187-21.9220.1983-15.5350.123-19.3460.1294-15.2520.089-16.1050.0945-14.7710.070-15.6980.0746-14.1880.057-14.0090.061

以上陣列優化算例表明：本文發展的麥克風相位陣列設計方法能夠根據試驗具體需求，優化設計出性能優良的陣列方案，且優化效率極高，滿足聲學試驗過程中隨時改進麥克風陣列的特殊需求。對最大旁瓣水平進行優化時，陣列單元沿螺旋線分布有向陣列中心聚集的趨勢，同時分辨率會略變差。相反，對陣列分辨率進行優化時，陣列單元沿螺旋線分布有向陣列邊緣移動的趨勢，最大旁瓣水平則會略變差。可見，最大旁瓣水平和分辨率這兩個性能指標在一定條件下是此消彼長的關系，無法同時優化到最優值。陣列設計工作需要考慮聲學試驗的聲源強度、特征尺寸等具體因素，在一個指標滿足基本約束的情況下，盡量提升最重要的核心指標。作為約束的指標可能會有所下降，但仍滿足基本需求，而核心指標的大幅提升則能夠明顯改善試驗測量結果的精準度。

2.3 矩形陣列設計

該陣列優化設計方法具有較強的可拓展性，只需針對參數化部分進行修改，即可應用于其他形式的陣列設計。針對81通道的1m邊長矩形陣列，將陣列單元的橫、縱坐標作為設計參數。以陣列單元在平面內的均勻分布作為初始方案，通過對陣元分布趨勢的優化，提升陣列最大旁瓣水平。圖6給出了優化前后矩形陣列單元分布示意圖。

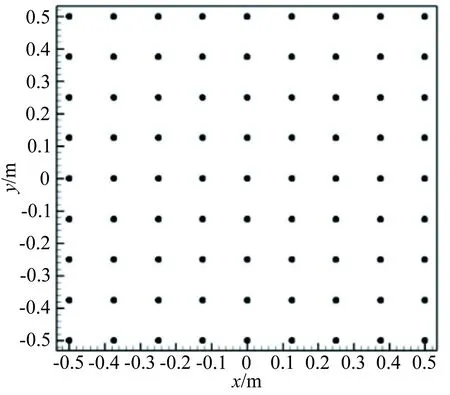
(a) 初始矩形陣列

(b) 優化矩形陣列

Fig.6ComparisonofinitialarrayandMSLoptimizedrectangularmicrophonearray

圖7給出了2kHz模擬聲源下陣列響應云圖，可見旁瓣水平有明顯改善。表5給出了1～6kHz頻率下陣列性能對比數據，優化陣列的最大旁瓣水平改善顯著，分辨率略變差。其中，聲源頻率為2kHz時，優化后矩形陣列最大旁瓣水平改善了4.2dB，提升約35.85%；分辨率下降約5.62%。整體而言，陣列性能有明顯提升。

(a) 初始矩形陣列結果

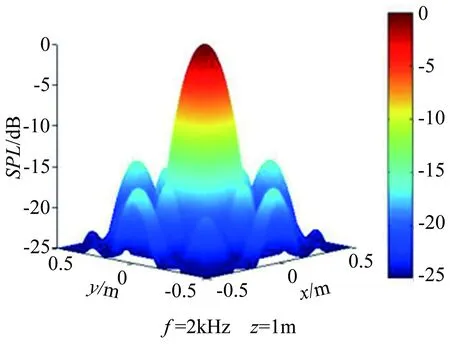
(b) 優化矩形陣列結果

Fig.7ResponsesofinitialarrayandMSLoptimizedrectangularmicrophonearrayresponses

表5 初始陣列與優化矩形麥克風陣列性能Table 5 Performance of initial array and optimized rectangular microphone array

3 結 論

將基于Kriging代理模型的遺傳算法引入麥克風相位陣列設計研究中，形成了高效率麥克風相位陣列設計方法，得到研究結論如下：

(1) 陣列優化結果表明：該優化設計方法可以根據試驗研究的具體需求進行麥克風相位陣列設計，有效提升麥克風相位陣列的分辨率或最大旁瓣水平性能，是一種可靠實用的麥克風相位陣列設計方法。

(2) Kriging代理模型的引入使得陣列優化設計過程耗時極短，可以滿足聲學風洞試驗中隨時針對聲源特點而改進麥克風相位陣列的特殊應用需求，有利于改善聲學風洞試驗測量數據的精準度，顯著提升試驗效率。

(3) 麥克風相位陣列的兩個主要性能參數(分辨率和最大旁瓣水平)通常無法同時達到極值，陣列設計時需要根據試驗測量的實際需求，搜尋陣列性能的最佳平衡點。

(4) 該陣列優化設計方法具有較強的可拓展性，針對參數化部分進行修改后，即可應用于其他類型陣列的設計工作。