應用分形理論研究飽和土壤滲透率
陳 卓, 王在敏, 許 模, 吳冠男
(成都理工大學 地質災害防治與地質環境保護國家重點實驗室, 成都 610059)
0 引 言
土壤作為典型的多孔介質,其孔隙大小、毛細管彎曲性、孔隙表面形貌等都具有隨機性、不規則性,但微觀結構在某個或多個尺度內顯示出自相似特征。因此利用分形理論刻畫土壤內部結構與滲透率的聯系成為研究土壤滲透率新的思路與方向。
Taylor[1]研究顯示土壤孔隙形態粒徑具有一定的自相似性和尺度不變性,Avnir等[2]用分子吸附技術研究巖石孔隙結構后,提出多孔介質具有分形孔隙結構,Kaze等[3-4]利用SEM對多孔的砂巖孔隙結構進行了基于分形概念的表征;Rieu等[5]借助于Sierpinski地毯圖案提出了孔隙分布的分形模型。由于科技的發展,隨著分形理論逐漸被引入到土壤物理學研究中,學者展開了土壤滲透率等水力特性參數與其結構之間的關系的一系列研究[6-15]。為了探究土壤體積分形維數對土壤飽和滲透率的影響,本文通過對不同配比的石英砂粒進行滲透實驗求得不同配比下的砂礫滲透率,結合砂粒的體積分形維數得到了不同土壤顆粒體積分形維數的滲透率。
1 材料與方法
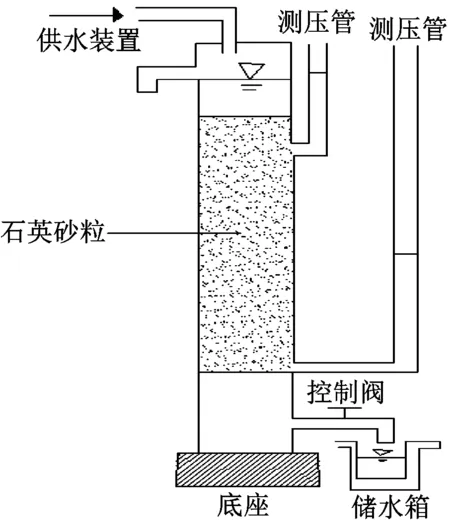
實驗選用60、80、100目的石英砂粒通過不同質量配比5種不同的土壤試樣,分別為:① 100%60目(A);② 60目∶80目=1∶1(B);③ 60目∶80目=1∶3(C);④ 100%80目(D);(5)60目∶80目∶100目=1∶1∶1(E)。實驗裝置示意圖如圖1所示,由試樣筒、測壓管以及供水裝置組成。試樣筒高60 cm、內徑10 cm,試樣筒上的兩個出水孔由橡膠管連接到測壓管上,兩個出水口的位置分別位于20 cm和40 cm處。
實驗根據達西公式計算滲透系數:
(1)
式中:Q為滲透流量(出口處流量);A為過水斷面的面積;H1、H2分別為石英砂柱兩個測壓管的水頭;L為石英砂柱的長度;I為水力梯度;K為滲透系數。
實驗測得的不同試樣的滲透系數K分別為:A型1.208 mm/s,B型0.445 mm/s,C型0.206 mm/s,D型0.152 6 mm/s,E型7.737 μm/s。
2 結果與分析
2.1 土壤粒徑分布的分形特征
運用激光粒度分析儀對滲流實驗的石英砂粒進行顆粒粒徑分析,得到5種土樣的顆粒級配圖,如圖2所示。
太沙基認為,土壤的粒徑特性主要由含量為20%的細土粒而定,即d20以下的細粒對土體性質有較大影響。謝定松等通過對粗粒土滲透系數影響因素的分析認為,控制土體滲透系數的代表性粒徑應為d21。
通過對比圖2中5種不同級配曲線和每種土樣所對應的滲透系數,發現當小于0.1 mm細土粒所占比重增加時,土樣的滲透系數相應降低,細土粒比重越大,滲透系數降低的幅度越大。但是,細土粒對于土體滲透性質的影響只能作趨勢性的判斷,經驗性較強,沒有從函數關系的角度對其進行精確刻畫。
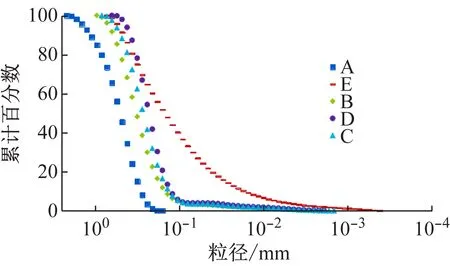
圖2 不同土樣顆粒級配圖
隨著分形理論在土壤物理學中的應用不斷加深,且由于土壤顆粒粒徑具有分形特征。因此運用分形維數刻畫顆粒粒徑分布特征成為熱點。本文應用Tyler等[13]的三維體積分形維數模型計算土壤體積分形維數,
(2)
式中:V為顆粒的體積;δ為測定的尺度;di為土壤顆粒粒徑;V0為土壤顆粒總體積;dmax為粒級分級中的最大粒級;D為體積分形維數。
式(2)兩邊同時取對數,得到體積分形維數的關系式:
(3)
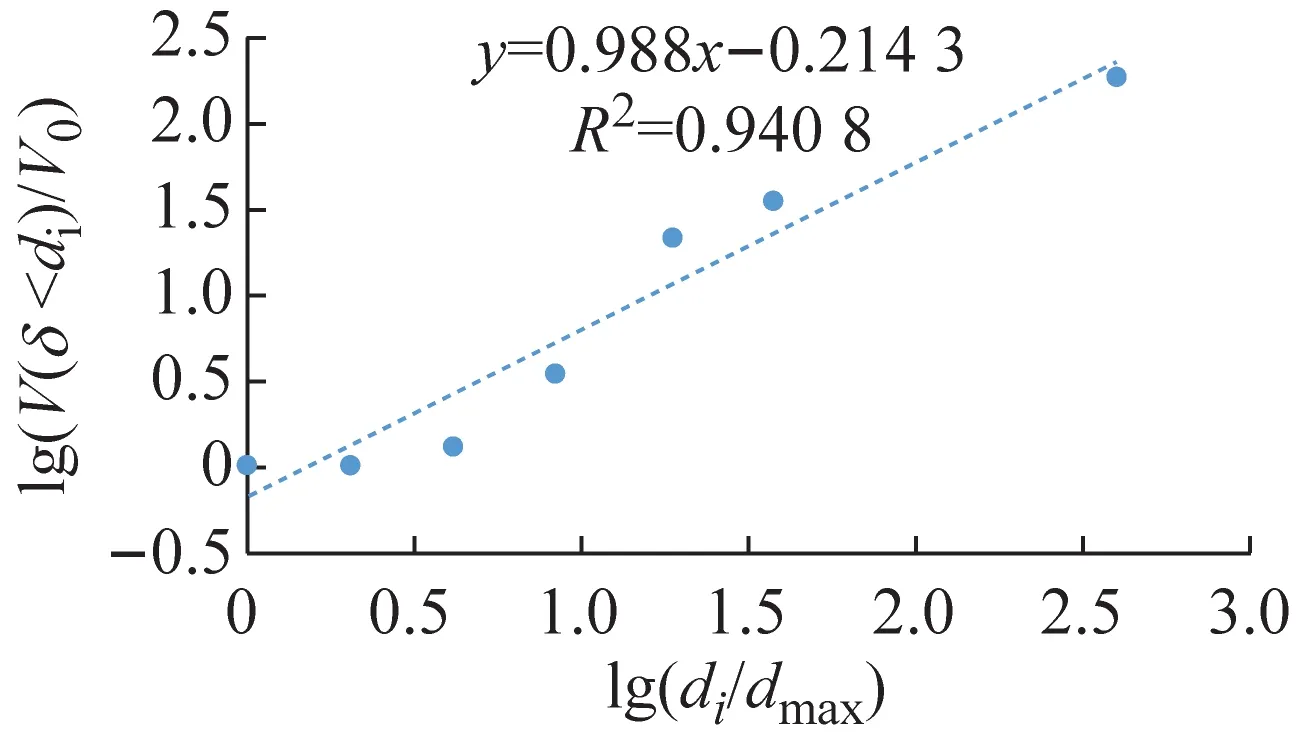
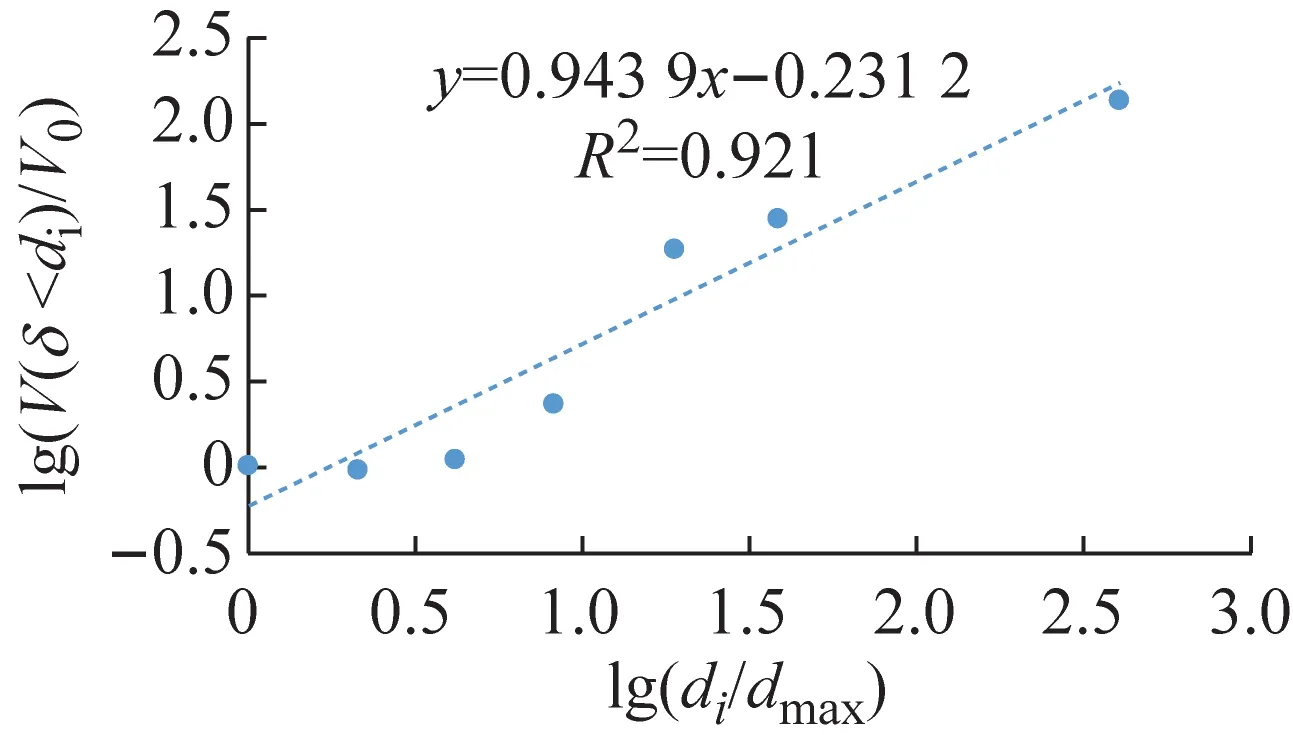
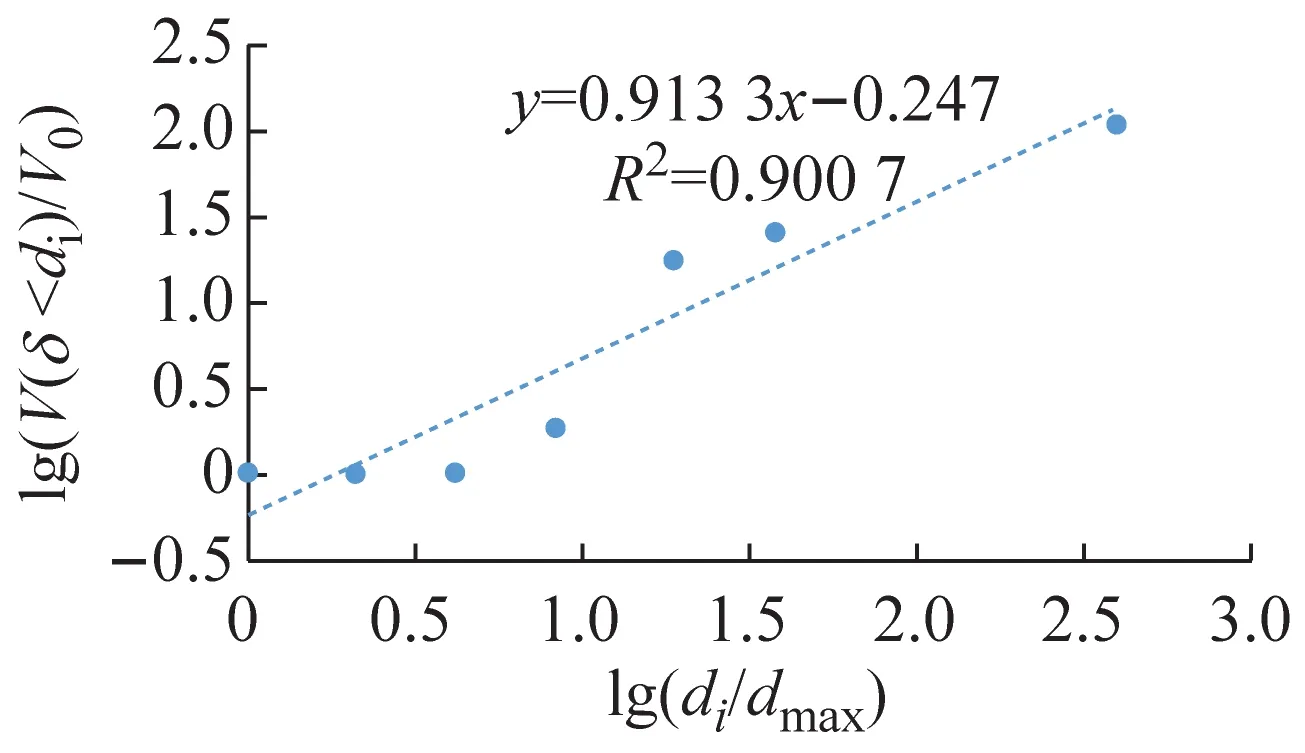
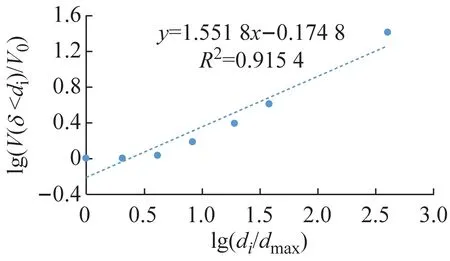
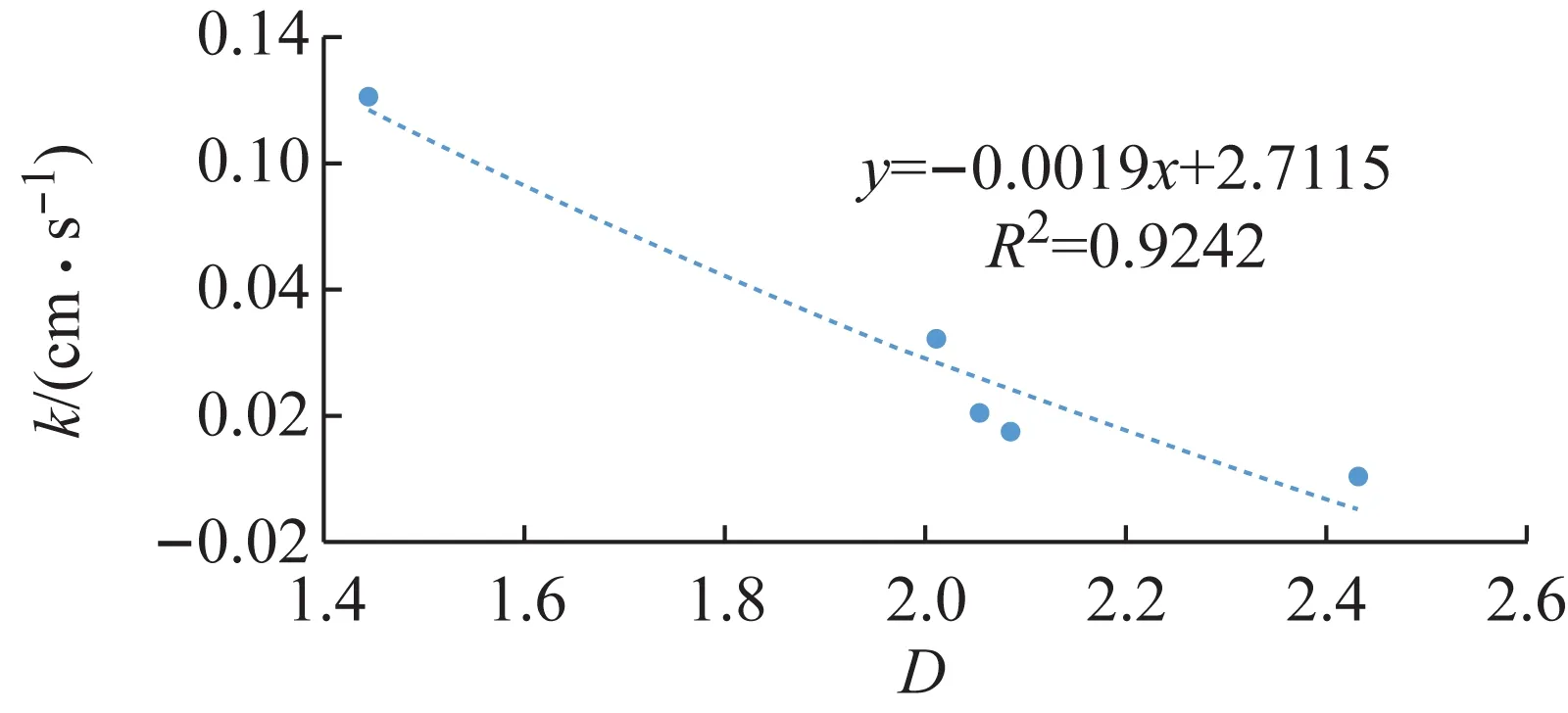
根據顆粒粒徑分析實驗的實驗數據,土壤的分級標準選用美國農業部分類系統[12],將粒徑分為:極粗砂(1~2 mm)、粗砂(0.5~1 mm)、中砂(0.25~0.50 mm)、細砂(0.10~0. 25 mm)、極細砂(0.05~0.10 mm)、粉砂(0.02~0. 05 mm)和黏粒(<0.02 mm)7個等級。以lg(di/dmax)為橫坐標;lg(V(δ 應用線性回結果歸計算出5種土樣粒徑分布的分形維數D分別為:A型1.448 2,D型2.012 0,E型2.056 1,B型2.086 7,C型2.434 8。運用Excel擬合求得的體積分形維數函數關系式R2都超過90%,可信度高。發現土壤顆粒體積D的增長幅度與土壤滲透系數K的增長幅度呈正相關。 土壤顆粒體積分形維數反映顆粒粒度分布的一個特征,土壤顆粒平均粒徑影響土壤顆粒體積分形維數。 根據McManus 矩算法: (a) A型 (b) B型 (c) C型 (d) D型 (e) E型 (4) 式中:MZ為顆粒平均粒徑;m為顆粒粒徑;f顆粒粒徑所占百分比。求得MZ:A型660.780 μm,B型257.53 μm,C型213.51 μm,D型377.11 μm,E型313.04 μm。 根據MZ的數據與相應土壤的D,運用Excel進行了關系擬合,見圖4。得到D數與MZ的關系式: D=-0.001 9MZ+2.711 5 (5) 據圖4知,函數關系式(5)的R2為0.924 2,可信度高,表明D與MZ呈線性負相關,MZ越大,D越小。 土壤的顆粒粒徑分布具有分形特征,D影響著滲透率k。對D與k的關系進行擬合,結果如圖5所示。 圖5 k和D的關系 根據圖5得到D與其飽和時的k的對數關系式: k=0.244 lnD+0.206 9 (6) 土壤滲透系數與滲透率的關系為: K=k(ρg/μ) (7) 式中:K為滲透系數;k為滲透率;ρ為流體的密度;g為重力加速度;μ為流體的動力黏滯系數。由于實驗中都是由自來水作為達西滲流實驗中的流體,故常數ρ、μ是相同的,g也是相同的,因此,k與K呈正比關系,即k=nK,其中n為常數。 因此,D與其飽和時的k的關系式為: (8) 根據式(5)初步擬定D與k的對數關系通用形式為: (9) 式中:A、B為經驗常數。 根據式(9)知,土壤顆粒體積分形維數與飽和土壤滲透率呈對數關系,R2達到0.952,可信度高。顆粒體積分形維數越大,土壤滲透率越小。 土壤顆粒體積分形維數取決于土樣的顆粒級配曲線,對于描述土樣性質具有整體意義。因此土壤顆粒體積分形維數對于土壤飽和滲透率的影響經驗性質更少,具有物理意義。相對來說,以前描述顆分的參數如:標準偏差,偏度,特征粒徑,不均勻系數等是從顆粒級配曲線的局部刻畫其特征,具有經驗性和局域性,并不具備單獨描述顆分性質的能力。因此運用土壤顆粒體積分形維數能夠更加全面地從土壤顆粒粒徑分布角度描述土壤滲透率,且兩者之間的函數關系式比較簡潔,式內的參數易于求得。但是式(9)中的A、B兩個參數的物理意義不明確,需要進一步探索。 本文通過滲流實驗以及顆粒粒徑分析實驗,將土壤滲透率與顆粒粒徑分形維數結合,通過數據分析得到以下結論: (2) 土壤滲透率與顆粒粒徑體積分形維數關系式D=-0.001 9Mz+2.711 5,R2為0.924,可信度高。表明土壤體積分形維數與土壤顆粒平均粒徑呈線性負相關,土壤顆粒平均粒徑越大,土壤顆粒體積分形維數越小。 (3) 本文通過室內物理實驗從土壤顆粒體積分形維數角度解釋了土壤滲透率的影響因素,有望對飽和土壤滲透率進行可靠的預測。 土壤粒徑分布特征對于土壤中的地下水運移尤為重要,本文通過室內物理實驗,基于多孔介質分形理論對土壤體積分形維數與土壤飽和滲透率的關系進行了初步研究,由于室內實驗條件的局限,不能完全模擬野外土壤的實際情況,可針對自然界實際情況進行相應的野外現場實驗。自然界中的土壤多數處于非飽和狀態,在非飽和狀態下,土壤體積分形維數對于土壤中地下水的運移的影響有待進一步研究。隨著土壤和地下水污染日益嚴重,掌握地下水溶質在土壤中的運移規律對于治理地下水和土壤污染尤為重要。探索土壤微觀結構分形特征對于污染物遷移的影響可以成為新的研究方向。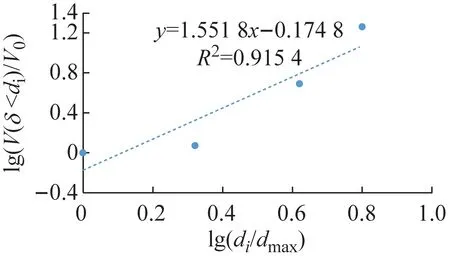
2.2 D對滲透率影響
3 結 論

