相控陣超聲換能器延時法則可視化分析

高世凱 韓 冬 安宏慶 李學雷

?

相控陣超聲換能器延時法則可視化分析

高世凱 韓 冬 安宏慶 李學雷

（西安航天動力機械有限公司，西安 710038）

針對相控陣超聲檢測技術延時法則的直觀性問題，采用數學建模方法，建立并分析研究二維、三維空間中相控陣超聲換能器聲束延時法則數學模型。同時建模分析凹凸曲面構件中的延時法則。通過可視化處理方法，得出相控陣超聲換能器延時法則的直觀量化結果，為選取相控陣檢測技術的最優化工藝參數提供了理論依據。

相控陣；超聲換能器；延時法則；可視化；數學模型

1. 引言

超聲相控陣技術的特點是各個陣元晶片可被儀器控制單獨激勵，因其獨特的優勢及優于常規超聲檢測的技術特點，近幾年在工業無損檢測領域越來越受到重視，并得到了廣泛的應用[1，2]。相控陣換能器可通過電子控制，實現聲束的偏轉和聚焦，無需更換探頭就可以實現局部區域內的多角度全方位掃查。超聲檢測通常對物體內部的某一局部區域進行原理成像，為此，必須對這一局部區域進行聲束掃描。現階段，聲束掃描最佳方式為相控陣法[3]。超聲相控陣檢測通過控制換能陣各個陣元延遲及變跡，改變各個陣元發射或接受超聲信號的相位關系，從而實現超聲檢測聲束的聚焦偏轉，達到檢測目的。壓電復合晶片在受到激勵信號后產生超聲波束，聲束參數均可通過儀器內置軟件進行相應的調整。由于相控陣換能器可將各聲束在焦點處相干疊加，使得檢測信號的信噪比有了顯著提高，從而更易檢測出缺陷[4]。

研究分析換能陣在不同檢測工藝要求下的延時規律，為不同的檢測工藝提供合理的延時法則。常規超聲探頭因無法實現聲束的靈活偏轉和動態聚焦，故在遠離聲束軸線及與聲束成一定角度位置的缺陷容易漏檢，相控陣超聲技術以其動態聚焦和聲束偏轉的特點，可減少無損檢測漏檢情況及提高檢測效率。利用可視化手段及MATLAB軟件仿真技術[5]，研究掌握換能陣延時法則，合理設置檢測工藝參數，提高相控陣超聲檢測技術的效率。

2 相控陣換能器二維聲束延時法則模型

2.1 聲束的聚焦和偏轉

線性超聲換能陣施加延時法則后聲束偏轉示意圖如圖1所示。該換能陣由個陣元構成，陣元中心距為，偏轉角度為。

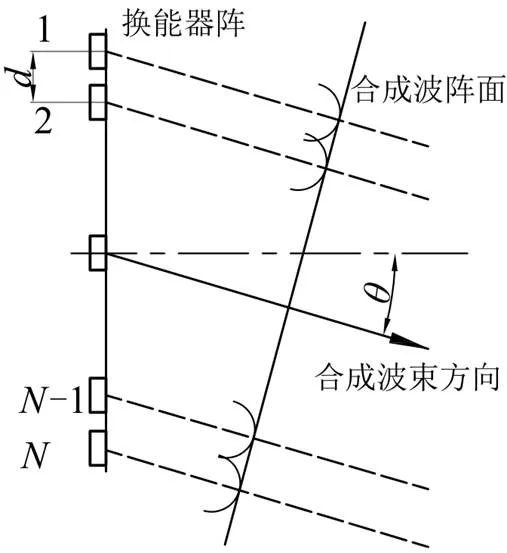
圖1 相控陣聲束偏轉原理示意圖

如果換能陣各陣元受到一致的激勵源，則其合成波束與換能陣表面垂直，不發生偏轉。若對換能陣各陣元按照一定的法則施加延時，則相鄰陣元由于延時法則的存在，不再垂直于換能陣表面，而是按延時法則與中心軸線成一夾角，從而使聲束偏轉。

根據圖1及波合成理論，相鄰陣元的延時時間為：

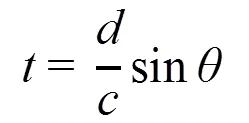
因此，第一個陣與第個陣元的延遲時間為：

（2）

由式2可知，通過改變偏轉延遲可改變超聲波束的偏轉角。對式（2）進行成像處理，得到聲束偏轉延時可視化曲線，如圖2所示。其中各參數選取：=1mm，=5500m/s，=45°。

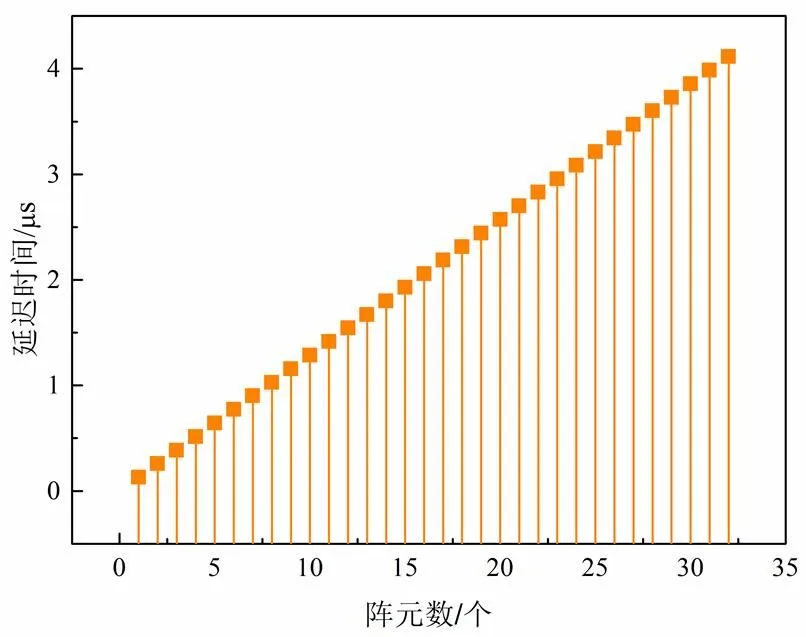
圖2 相控陣聲束偏轉延時曲線

由圖2相控陣聲束偏轉延時曲線可知，換能陣聲束在只發生偏轉的情況下，延遲時間與陣元個數呈線性關系，因而聲束偏轉屬于最基本的一種換能陣延時法則，通過控制聲束偏轉延時，可控制換能陣聲束偏轉角。

相控陣聲束聚焦原理如圖3所示，以換能陣中心陣元為參考陣元，通過聲波合成原理，換能器發出的聲束在點聚焦。

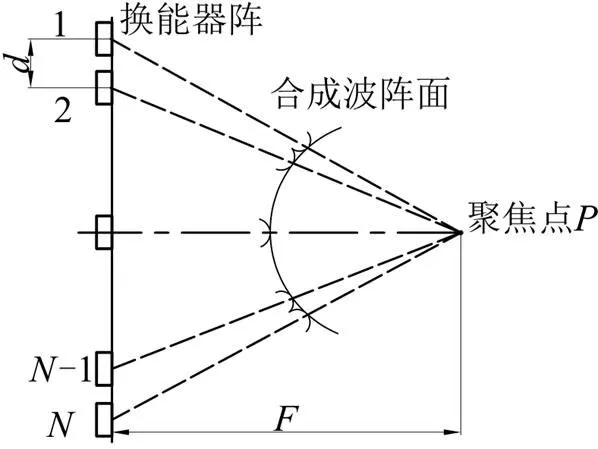
圖3 相控陣聲束聚焦原理示意圖

換能陣發射聚焦時，采用延時順序激勵陣元的方法[6]，使換能陣各陣元按設定的延時法則依次被激勵，從而在介質內形成新的波陣面，在聚焦點因波的同向疊加而增強，其余區域異向疊加而減弱，甚至消失。以換能陣中心陣元作為參考點，依據幾何光學原理，使各陣元發射的聲束在焦距為的點聚焦，由圖中幾何關系可求得各陣元的激勵延遲時間為：

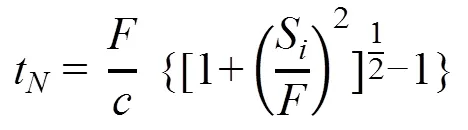
其中，S為第個陣元到陣列中心的距離，S=|[-(+1)/2]|，=1, 2…。

圖4 相控陣聲束聚焦延時曲線

可視化處理式（3），得到圖4相控陣聲束聚焦延時曲線，其中=1mm，焦距=30mm，=5500m/s。由式3可知，通過改變發射聚焦延遲t，可改變焦距。換能陣聲束聚焦延時曲線如圖4所示，由圖可知，聚焦延時時間在中心陣元處出現延時峰值，在兩邊陣元處為0。隨著陣元數目的增加，延時時間呈現先上升再下降的趨勢。因此可以通過改變陣元數，控制發射聚焦延遲時間，調節動態焦距，從而實現深度方向的聚焦掃查。

2.2 偏轉聲束的聚焦

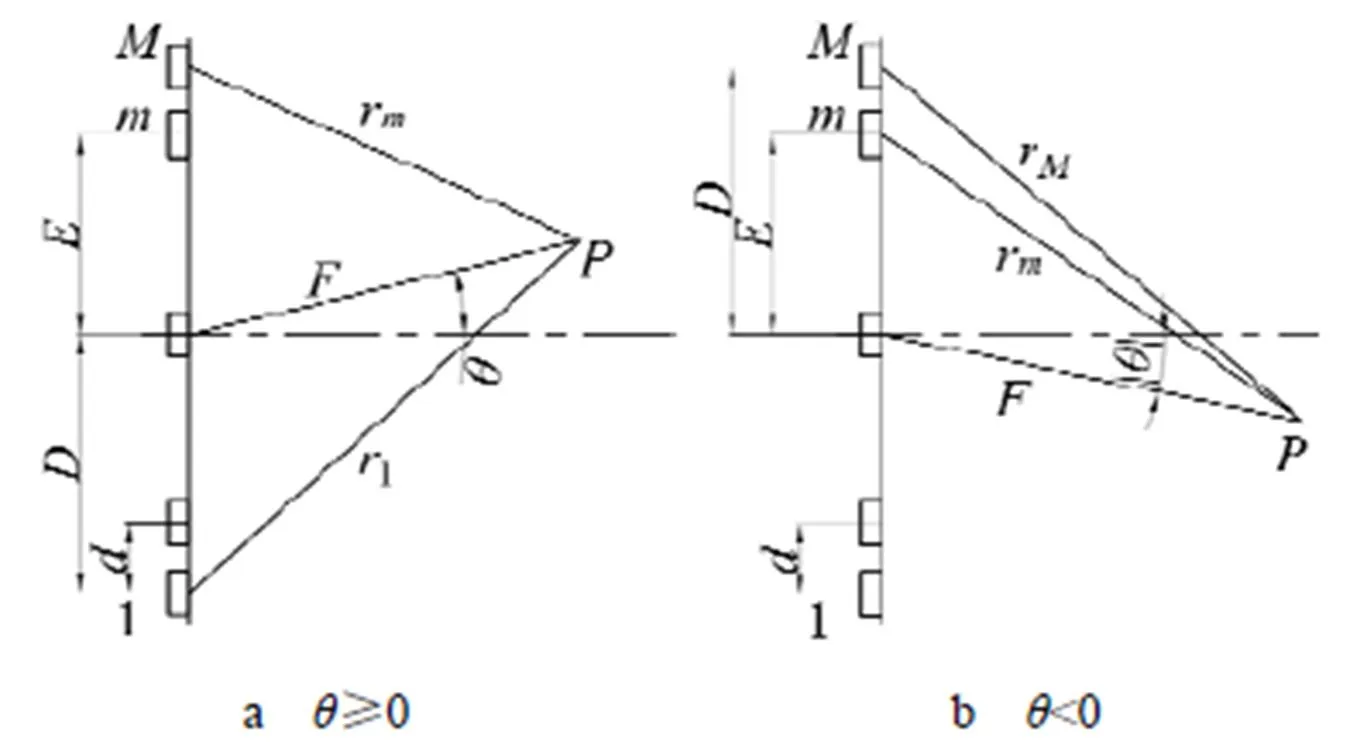
圖5 相控陣偏轉聲束聚焦原理示意圖

有許多方法將相控陣換能器陣列中二維聲束偏轉和聚焦延時法則的模型參數優化設計[7]。偏轉聲束的聚焦原理見圖5a、5b，為偏轉聲束與換能陣中心軸的偏轉角度，為偏轉聲束沿偏轉方向的焦距。因為偏轉角度存在正負兩種情況，所以偏轉聲束聚焦分兩種情況。

由圖5a及合成波束原理，第一個陣元與陣列中心的距離為：

=(-1)/2 （4）

因此，第個陣元中心的位置可表示為：

=[(-1)-]（5）

式中=(-1)/2。

在≥0時，分析相控陣偏轉聲束聚焦延時時間與陣元數的關系。如圖5a所示，為了得到將波束偏轉聚焦到點的延時法則，首先計算第個陣元中心傳播到點處需要的時間，t=r/。由圖5a可明顯看出，第一個陣元點到聚焦點的距離1是最大的，可以將延時法則簡單的設為：

據圖5a中的幾何關系和余弦定理，可得：

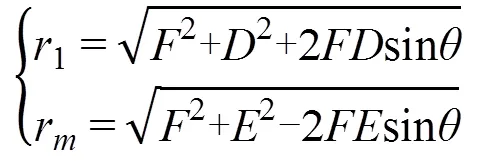
延時法則整理為：

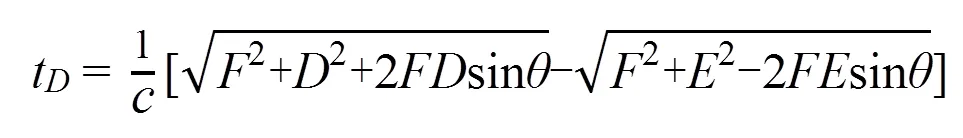
根據圖5b中的幾何關系，同理可得，<0時：

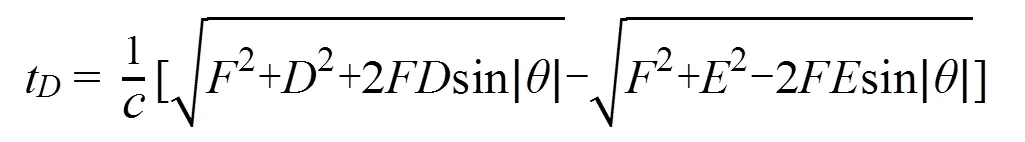
由式（8）、式（9）得出相控陣聲束偏轉聚焦延時曲線，如圖6所示，曲線為開口向下的半拋物線，在末端陣元處達到偏轉聚焦延時峰值，整個過程延時時間呈緩慢增加的趨勢，延時法則與儀器實際工作延遲規律一致。

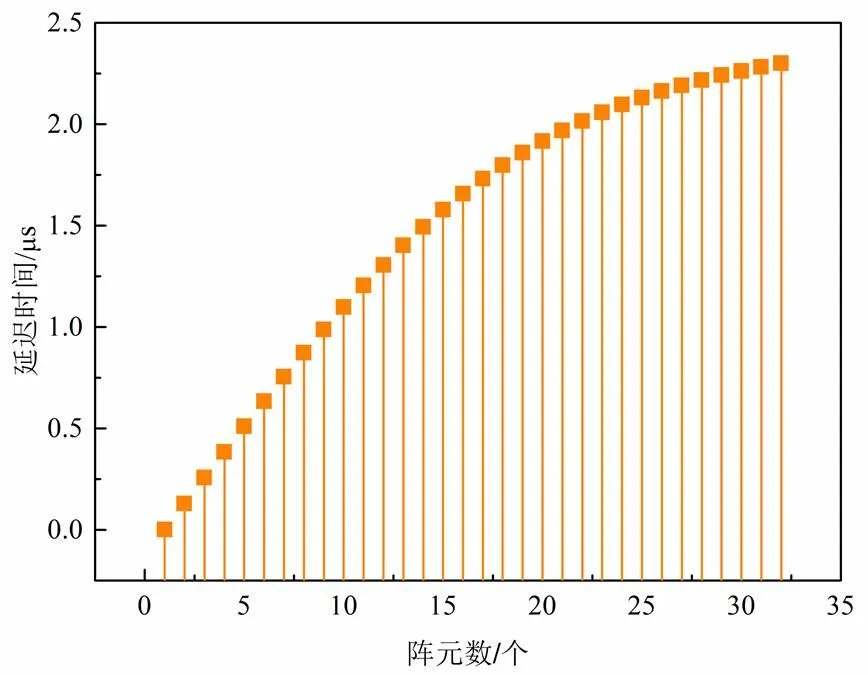
圖6 相控陣聲束偏轉聚焦延時曲線

對比分析圖2、圖4、圖6發現，三種不同情況下的延時法則各不相同，只發生偏轉時的延時法則最基本也最簡單，聚焦延時及偏轉聚焦延時法則相比之下較復雜，由此可知偏轉聚焦掃差可全方位檢測定位對缺陷。通過控制相應的延時參數，可以控制檢測工藝參數，全方位檢測。

3 相控陣換能器三維聲束延時法則模型

3.1 三維聲束控制方程

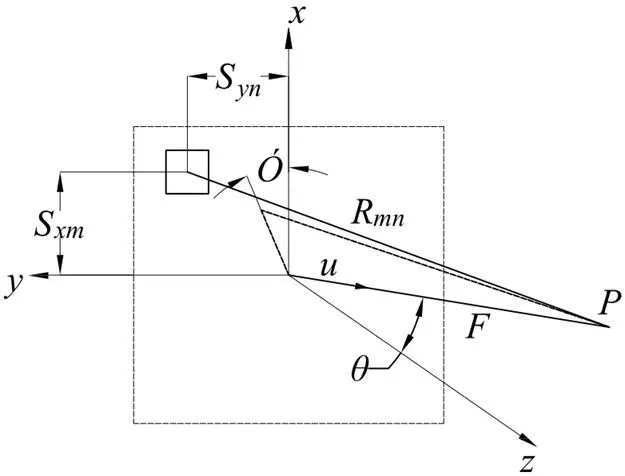
圖7 二維陣列波束控制聚焦參數示意圖

為二維陣列中的陣元產生的三維空間單位矢量方向上的超聲波束控制聚焦參數如圖7所示。根據球坐標下計算公式，可得出在球坐標系(，)下的表達式為：

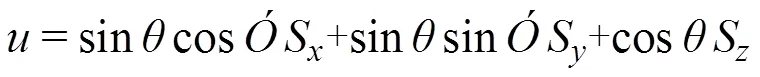
對陣列面應用線性延時Δt=/可以實現波束方向的控制，分析單個陣元中心的相位，得出延時為：

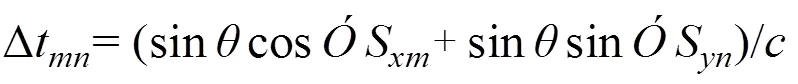
中心位置為：

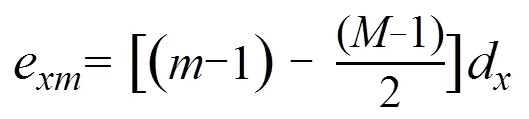
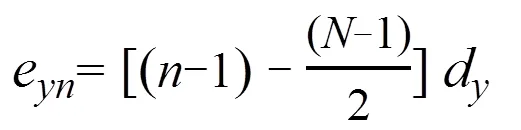
由于式11得到的延時包含正、負值，因此通過增加一個等于最大負值的常數延時來獲得合適的延時法則，即：

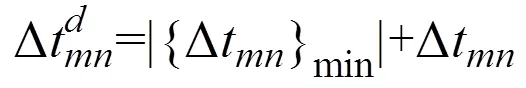
3.2 三維空間中聲束的偏轉和聚焦

由圖7可知，換能陣波場在點聚焦，焦距為，偏轉角為、，根據幾何關系，從陣元到點的距離可表示為：

通過優化處理，由式（11）可得出恰當的延時法則計算公式

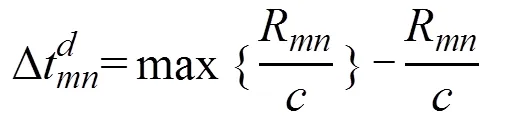
利用MATLAB軟件對式（16）進行仿真模擬[8]，得到以下二種換能陣延時法則。t為方向個陣元，方向個陣元陣列的延時矩陣。陣列在和方向的間距分別為SS，波束偏轉角為、，焦距為，介質中的波速為。

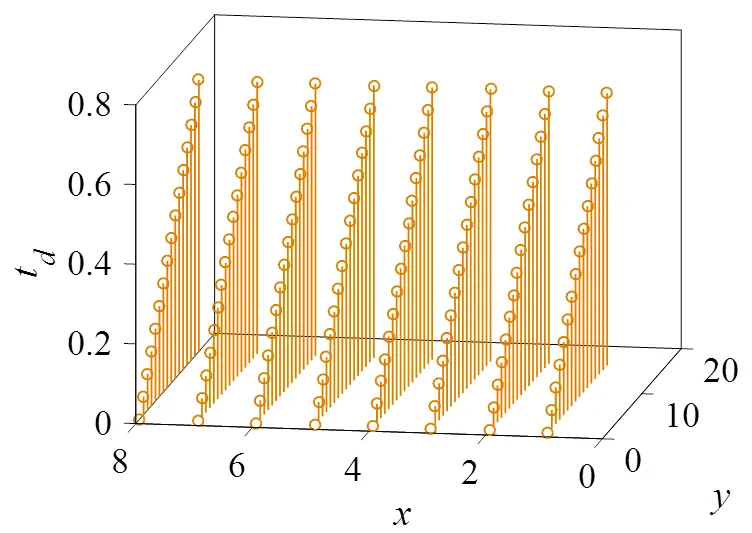
圖8 M=8，N=16個陣元的二維平面陣列平行于y軸波束偏轉的延時td

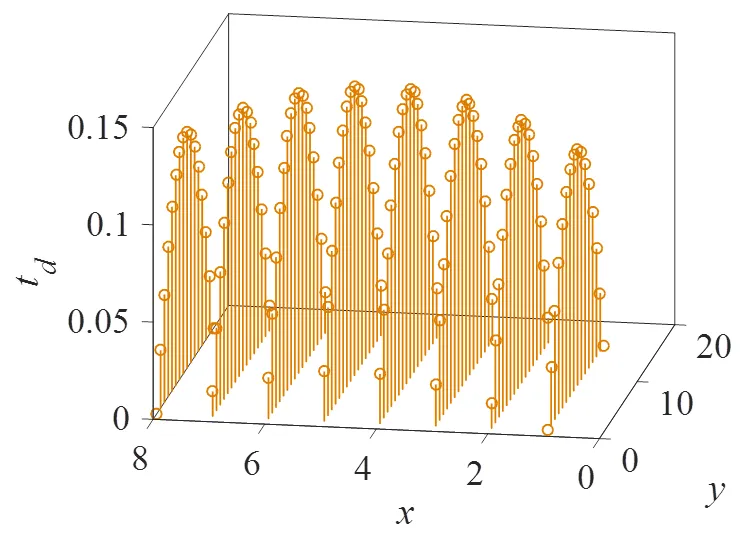
圖9 M=8，N=16個陣元的二維平面陣列沿z軸波束偏轉的延時td

如圖8、圖9所示，=8，=16陣元陣列輻射的延時法則例子，其中S=S=0.5mm。圖8表示=30°，=90°，=inf僅平行于軸偏轉的情況。由圖8可以看出，延時法則是包含于式（11）的線性函數。圖9考慮了同一陣列==0°，=10mm的聚焦情況，此時，在和軸方向上的延時法則呈二次方程規律。

對比分析換能陣二維聲束和三維聲束延時法則，二者的延時法則規律相同。但三維聲束延時法則表現形式為矩陣，二維聲束延時法則為單一數值。由式（15）可知，通過改變延時時間t，運用控制變量法，可分別控制參數、、，進而獲得三維聲束不同參數下的延時法則。

4 凹曲面構件延時法則模型

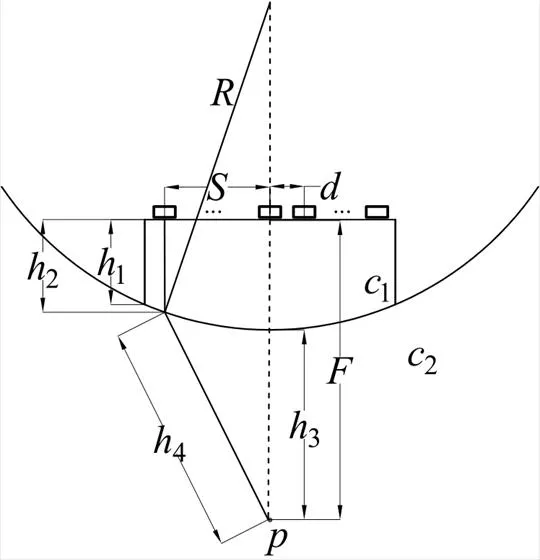
圖10 凹曲面構件延時聚焦模型示意圖

由于新技術和新工藝的發展，異形曲面件在實際生產中的應用越來越多。對曲面構件的無損檢測一直都是一個技術難點[9]。現實生產中，相控陣技術用于檢測曲面構件的耦合方法有兩種：楔塊耦合和柔性探頭耦合[10]。建模分析楔塊耦合過程的延時法則，并給出相應的延時計算公式。凹曲面構件延時參數模型示意圖如圖10所示。

由圖可知激勵陣元到中心軸線水平距離與陣元間距的關系為：

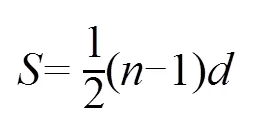
式中：為第個陣元，由圖10幾何關系可得到第個激勵陣元相對于中心軸線的延遲時間t為：

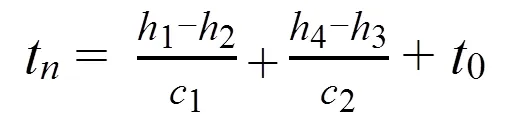
其中：1=2-(-(^2-^2)^(1/2))，2為凸型楔塊弧面部分最凸點到楔塊表面的距離；3為聚焦點深度即缺陷深度；4為折射點到聚焦點的距離；為折射點到聚焦點距離；1、2分別表示聲束在楔塊和工件中的傳播速度。

結合式（17）和式（18），可得到凹曲面構件延時法則t計算公式：

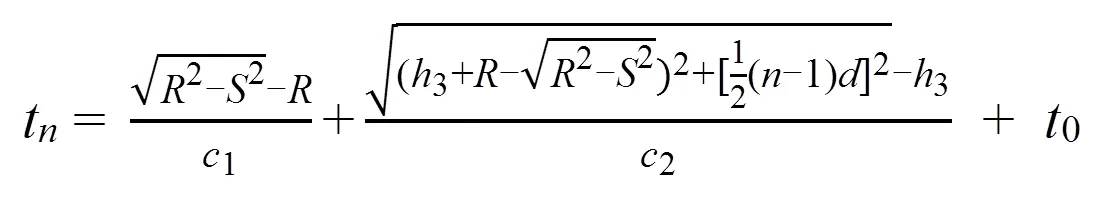
其中：0為一足夠大的時間常數，以避免t出現負的延遲時間。

對式（19）進行可視化處理，選取參數下：=1mm，2=10mm，3=15mm，=40mm，1=1500m/s，2=5500m/s。得到如圖11所示的凹曲面聲束聚焦延時曲線。

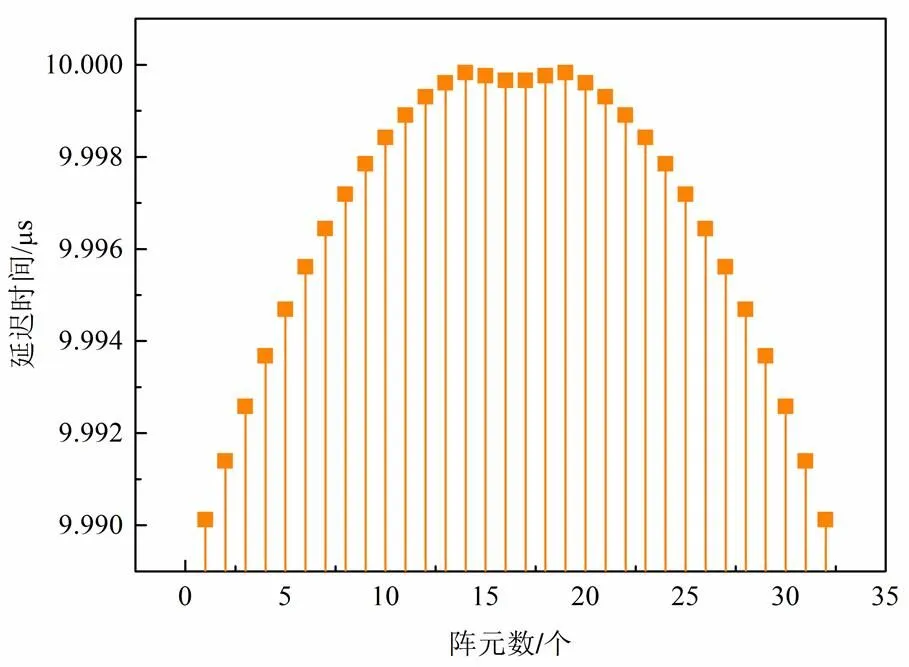
圖11 凹曲面相控陣聲束聚焦延時曲線

分析圖11可知，在上述模擬參數條件下，凹曲面聚焦延時法則不同于平面聚焦延時法則。凹曲面延時曲線在中心陣元兩側存在一個緩沖帶，延時峰值在此緩沖區域，此區域內聚焦延時變化不明顯，中心陣元左側呈先增加達到峰值后緩慢減小到中心陣元處的變化趨勢，中心陣元兩側變化趨勢對稱。

5 結束語

研究分析相控陣換能器二維、三維聲束延時法則，掌握了相控陣換能器的延時機理，得到以下兩點結論。

a. 二維聲束不同情況下延時法則各不相同，只發生偏轉時的延時法則最基本也最簡單，聚焦延時及偏轉聚焦延時法則相比之下較復雜。通過改變延時參數，可以達到對偏轉角和聚焦點的控制，從而實現聲束偏轉和動態聚焦。

b. 三維聲束延時法則，計算參數較多，因而較二維延時法則復雜，但二者規律相同。運用控制變量法，通過控制不同參數，可獲得三維聲束不同參數下的延時法則。通過可視化處理，得到相控陣超聲換能器延時法則的直觀量化結果，為進一步優化工藝參數提供理論依據。

1 Rao R T. Microelectronics packaging handbook[M]. New York:McGraw-Hill Publisher, 2001

2 Long Zhili, Wu Yunxin, Han Lei, et al. Dynamics of ultrasonic transducer system in thermionic flip chip bounding[J]. IEEE Trans on Components and Packaging Technologies, 2009(2): 261～267

3 楊平. 二維陣列相控陣超聲三維成像技術研究[D]. 北京：清華大學，2006

4 高鵬，李法新. 非線性超聲相控陣無損檢測系統及實驗研究[J]. 實驗力學，2014(1)：1～11

5 Jensen J A. Simulation of advanced ultrasound systems using field Ⅱ[C]. In Proceedings of 2004 IEEE International Symposium on Biomedical Engineering, 2004

6 Smith S W, Pavy H G, Ramm O T. High-speed ultrasound volumetric imaging system. I: Transducer design and beam steering[J].IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control,1992,38(2): 100～108

7 Weston M, Mudge P, Davis C, et al. Time-efficient auto-focusing algorithms for ultrasonic inspection of dual-layered media using full matrix capture[J].NDT&E Int，2012(47): 43～50

8 Dziewierz J, Gachagan A. Computationally efficient solution of snell’s law of refraction[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control,2013(6): 1256～1259

9 張元亮，張洪潮，趙嘉旭，等. 高端機械裝備再制造無損檢測綜述[J]. 機械工程學報，2013，49(7)：80～90

10 李衍. 柔性相控陣換能器用于形狀不規則工件的超聲檢測[J]. 無損探傷，2013(5)：1～5

Visualization Analysis of Phased Array Ultrasonic Transducer’s Delay Rule

Gao Shikai Han Dong An Hongqing Li Xuelei

(Xi’an Aerospace Power Machinery Co., Ltd., Xi’an 710038)

For the intuitive problem of phased array ultrasonic detection technology's delay rule, mathematical modeling and visualization processing methods are adopted. The mathematical model of phased array ultrasonic transducer ultrasonic sounder delay law in two-dimensional and three-dimensional space was established and analyzed. At the same time, the time-delay rule modeling of concave-convex surface components was analyzed. Through visual processing, the visual quantification results of phased array ultrasonic transducer delay rule are obtained, which provides a theoretical basis for the selection of suitable process parameters for phased array inspection technology.

phased array；ultrasound transducer；delay rule；visualization；mathematical model

高世凱(1993)，碩士，材料科學與工程專業；研究方向：超聲無損檢測。

2018-07-02