基于網絡拓撲與節點元數據的社團檢測算法
劉宇廷,畢海濱,郭 強,倪穎杰
(江南計算技術研究所,江蘇 無錫 214000)
0 概述
不同領域多樣化的系統可以表示為復雜網絡,例如科技系統、生物系統和社會系統[1]。針對復雜網絡研究的一個熱門方向是社團檢測,社團結構在復雜網絡中普遍存在[2]。通過挖掘網絡中的社團,可以幫助理解網絡拓撲結構特點,揭示復雜系統內在功能特性,理解社團內個體關系及行為的演化趨勢[3]。
傳統社團檢測方法基于網絡拓撲結構的統計特性建模進行分析與挖掘,研究人員通常假設得到的社團能夠表示具有相似特性或功能的節點集合。當前,一些研究已經證實了這個假設下得到的社團與網絡中元數據代表的團組是有區別的[4]。所以,許多研究人員期望能夠結合其他信息進行社團檢測,以發現網絡中的真實社團結構。
在真實復雜網絡中,網絡除了拓撲信息之外,還有節點上的元數據與邊上的元數據。例如,社交網絡[5]如新浪微博包含用戶的個人信息(姓名、年齡、愛好等),引用網絡包括用戶的姓名、關鍵詞和文章的摘要信息、郵件網絡中發送郵件的內容等。通常屬于一個社團中的節點一定共享了某些相似的屬性,反之可以認為節點的屬性影響了社團的結構,結合這些元數據將會提高社團檢測的準確性。近年來,研究者提出許多社團檢測算法,以期能夠通過元數據提高社團檢測的準確程度。文獻[6]利用2個節點之間共同好友的個數衡量節點之間的相似度,但是這個方法需要遍歷整個網絡,復雜度高;文獻[7]利用譜聚類算法找到初始劃分,利用節點的度、內度、外度建立條件概率表,選擇一部分最有可能的點作為根節點,構建貝葉斯網絡來找到最優社團結構;文獻[8]通過定義節點與節點、節點與社團之間的互動力作為社團檢測的指標;文獻[9]提出一種基于自然最近鄰居概念的社團檢測算法CD3N算法,以結構相似度為基準,構造網絡中節點的自然鄰居從而發現社團結構;文獻[10]指出當前很多方法只是基于網絡中邊的連接信息而忽視了節點上的信息,將邊與節點信息同時存在的網絡建模為NSBM,并研究基于似然推理的算法;文獻[11]提出通過改進基準網絡建模,將節點上的元數據(metadata)社團編號融合到模型中,以自動判斷這種元數據能否幫助網絡劃分,使得到的網絡劃分評價分數更高。但是算法中使用的元數據是社團歸屬標簽與年齡、性別等單一屬性,在刻畫節點特征上并不完整,例如社交網絡中一個節點的描述通常是一段文字、圖片等信息。
針對文獻[11]算法存在的問題,本文提出基于網絡拓撲與節點元數據的社團檢測算法CDNTNM。首先假設網絡中節點具有混合高斯分布,構建節點元數據復雜分布的基準網絡;然后建立融合網絡結構與節點元數據的網絡模型,研究混合高斯模型與基準網絡模型的融合方法;最后分析真實網絡數據樣本分布,提出特征選擇方法。
1 基于隨機塊模型的網絡建模
1.1 隨機塊模型
隨機塊模型[12]通常建模為包含社團結構的網絡,用于輔助社團發現。隨機塊模型通常假設網絡中社團數量是固定的,網絡中的節點一定歸屬于其中某個社團,處于不同社團中的節點以概率prs建立連邊。調整同一個社團內節點之間邊連接的概率,可以生成符合社團結構定義的網絡結構,即社團內部連邊密集而社團之間連邊稀疏,隨機塊模型的似然函數為:
(1)
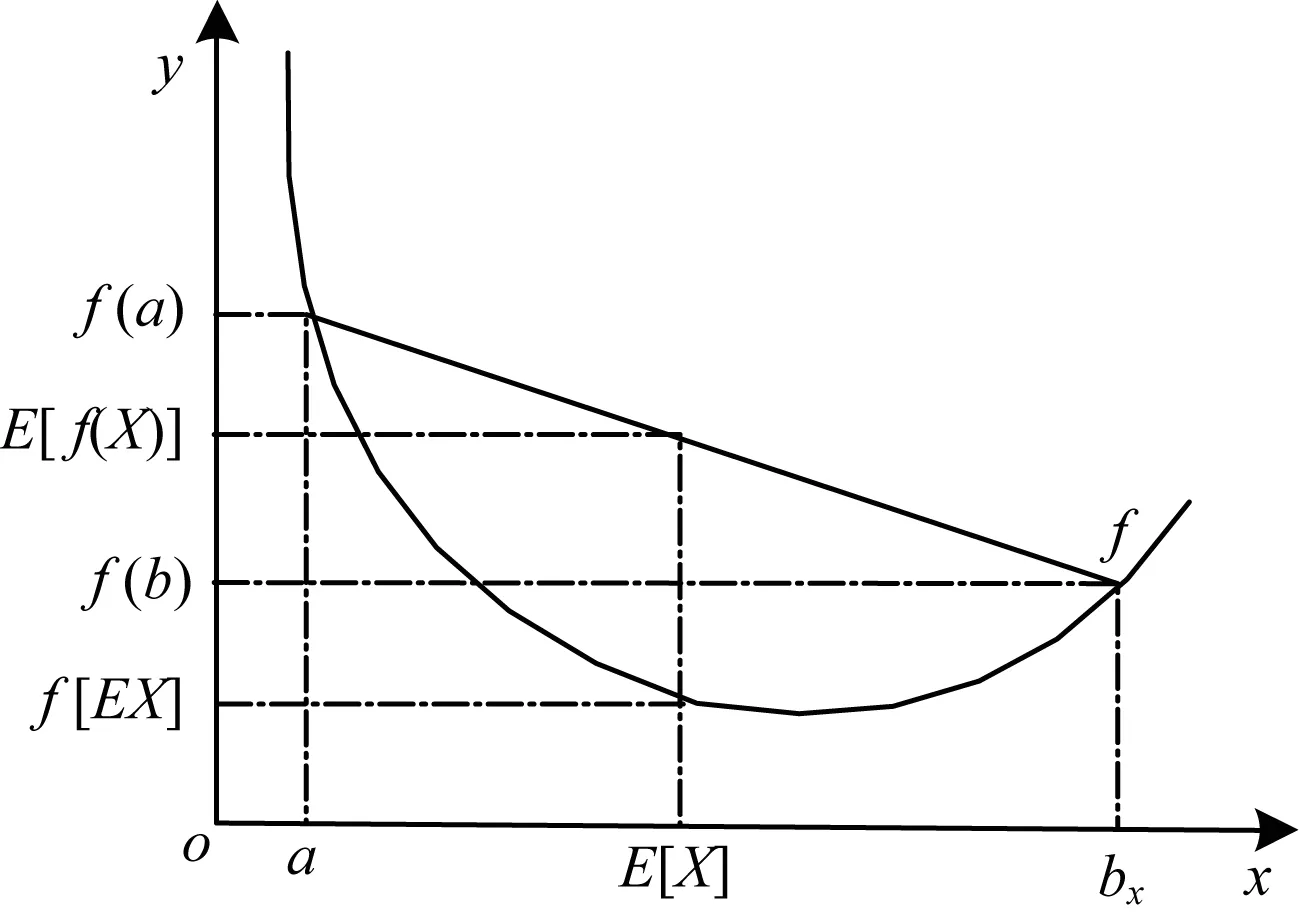
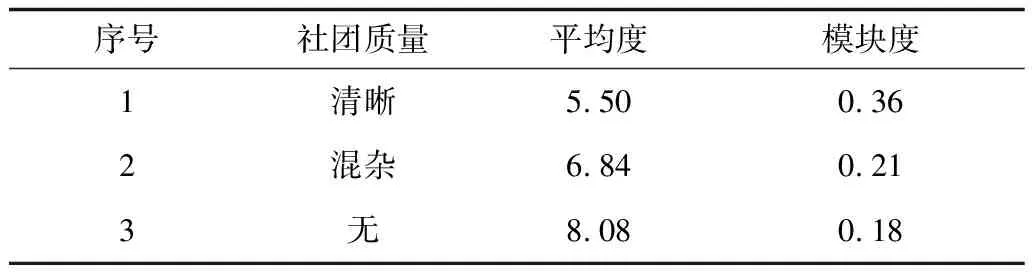
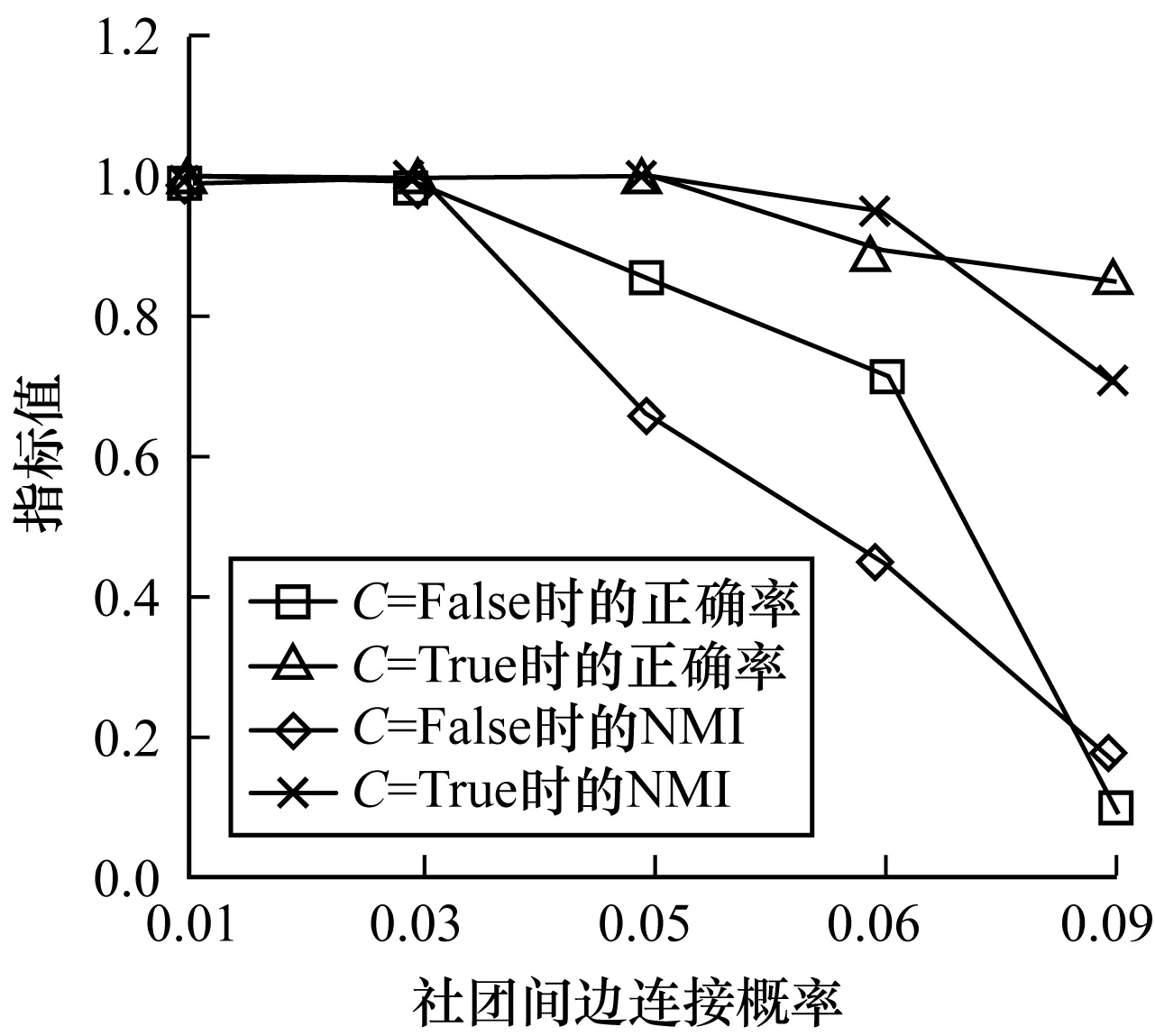
其中,Aij代表網絡的鄰接矩陣中第i行第j列的元素,取值為1表示節點i和節點j之間存在連邊,取值為0表示不存在連邊,si表示節點i所屬的社團編號,i 真實復雜網絡具有“無標度”特性[14],而隨機塊模型不滿足這個特征,所以,在擬合現實世界網絡數據時效果很差。文獻[15]通過在塊模型中添加度數相關的變量,使得節點之間邊的概率prs能夠與節點度數匹配(如節點具有邊的總量),從而滿足“無標度”這個特性。改進后的模型中定義節點之間邊的概率為: puv=dudvθsu,sv (2) 其中,du為節點u的度數,θst是指定的參數,θsu,sv能夠讓模型適合任意度數序列,即度數分布。 真實復雜網絡中節點上的元數據通常呈現信息多、形式雜的特點,例如:一個校園社交網絡中學生具有性別、年齡、種族等信息;一個食品網絡顧客信息包含體重、愛好等信息。節點上的信息不僅具有標量信息和連續變量信息,甚至還有文本信息,無疑對社團分布影響非常大。通常具有相似信息的節點元數據構成的特征符合一定的分布,比如高斯分布。所以,在本文的實驗中,將這類具有多維度特征的向量建模為多維高斯模型。為方便觀察,實驗中使用二維高斯分布數據作為節點元數據,數據來自2個具有相同方差、不同均值的高斯分布,參數如表1所示,通過參數可以將2個分布的邊界控制為清晰與混雜。 表1 節點元數據分布參數設置 (3) 由隨機塊模型可知基于網絡拓撲結構的先驗概率模型為: (4) 基于這兩個模型生成網絡的似然概率為: (5) 其中,A為網絡的鄰接矩陣,Γ為參數γsx的矩陣,Θ為參數θst的矩陣。針對復雜網絡節點具有高維元數據的情況,可以定義:對于所有節點元數據X={x1,x2,…,xn},假設每個節點u分配到社團s的概率基于節點u的元數據xu,xu∈n,n≥1,定義概率為γsx,使用高斯混合模型對社團歸屬建模。高斯混合模型的概率模型為: (6) 對于每個節點的元數據xi,其由第k個高斯模型生成的概率為: (7) 其中,N(xi|μk,δk)為xi屬于分布k的后驗概率,如式(8)所示。 (8) 因此,基準網絡中每個節點社團分配的先驗概率模型為: (9) 最終得到基于這兩個模型生成網絡的似然概率為: P(A|Θ,π,μ,σ,x)= (10) 在上述式中,π為高斯混合模型的權值向量,μ、δ為高斯混合模型的均值矩陣與方差矩陣。通常可以使用EM算法求解式(9),通過估計模型中的參數,得到模型的最優解,從而得到社團分布。 設有函數f(x),x∈,如果?x有f″(x)≥0成立,則f(x)是凸函數。如果x是一個向量,而且其hessian矩陣H是半正定的(H≥0),那么f(x)是凸函數。如果f″(x)>0或者H>0,那么稱f(x)是嚴格凸函數。 Jensen不等式表述為:如果f是凸函數,X是隨機變量,那么E[f(x)]≥f(EX),特別地,如果f是嚴格凸函數,那么E[f(x)]=f(EX),當且僅當p(x=E[X])=1,即X是常量。這里f(EX)是f(E[X])的簡寫[15],其幾何表示如圖1所示。 圖1 Jensen不等式的幾何表示 給定的訓練樣本是X={x1,x2,…,xn},樣本之間相互獨立,對于每個樣本xi,存在隱含類別z使得p(x,z)最大。p(x,z)的最大似然估計公式如下: (11) 求解第1步是對極大似然取對數,第2步是對每個樣例的每個可能類別z求聯合分布概率和。但是直接求θ一般比較困難,因為有隱藏變量z存在,所以如果能夠確定z,則求解便可以化簡。 EM是一種解決存在隱含變量優化問題的有效方法。由于不能直接最大化(θ),因此不斷地建立(θ)的下界(E步),然后優化下界(M步)。可以簡單描述為:對于每一個樣本xi,用Qi表示該樣本隱含變量z的某種分布,且Qi滿足的條件是例如:要將動物分類,如果隱藏變量是體重,那么就是連續的高斯分布;如果按照隱藏變量是食肉或食草,那么就是伯努利分布。 由此可以得到以下公式: (12) (13) (14) (15) p(z(i)|x(i);θ) (16) 由上述推導可以發現,固定θ后,Qi(z(i))的計算公式就是后驗概率,解決了Qi(z(i))如何選擇的問題。這一步就是E步,建立(θ)的下界。接下來的M步,就是在給定Qi(z(i))后,調整θ,去極大化(θ)的下界(在固定Qi(z(i))后,下界還可以調整的更大)。(θ)是單調增加的,所以,算法在(θ)趨于不變時收斂。 將2.2節的推導應用到式(10)中,可以得到: logaP(A|Θ,π,μ,σ,x)= (17) (18) 由式(18)可以看出,Qi(z(i))為后驗概率分布,表達式為: (19) 對式(18)應用EM算法,可以得到CDMTMN算法對應的最優解,算法求解過程與EM算法中對應步驟描述如下: 1)CDNTMN算法初始化,輸入數據集G,檢測網絡G中的社團結構,得到模型似然概率值并輸出網絡節點社團歸屬分布Q。初始化Θ、μ、δ、π的值。 2)E步,固定參數Θ、μ、δ、π的值,使用它們計算社團后驗概率分布Q。 3)M步,固定Q,更新參數Θ、μ、δ、π的值。 4)計算似然值與評價函數,查看是否收斂。如果否,從第2個步驟開始執行。 5)算法收斂,算法結束,得到模型似然概率值與社團最優分布Q。 仿真硬件平臺為:E4310,8 GB,Win7 x64,對比算法選用Newman的算法[11]、FN算法[17]。 3.1.1 基準網絡生成 在電腦生成的基準網絡上測試算法性能,基準網絡基于Newman改進后的隨機塊模型生成。基準網絡的參數包括:網絡中社團數量K(定義K=2);網絡節點數量N;社團內部與社團之間邊連接概率的混合參數Γ,為K×K矩陣;網絡中節點元數據維度D;節點元數據邊界清晰參數C。 通過設置不同的參數,生成用來對比的基準網絡,實驗中使用的參數如表2所示。 表2 基準網絡參數 具有相同的節點規模N、節點上的元數據維度D與社團內邊連接概率pin,不同基準網絡通過社團間邊連接概率區分,為表征各個基準網絡的社團結構程度,通過調整社團間邊的連接概率,將基準網絡分為3個等級:清晰,混雜,無,分別對應具有明顯的社團結構、社團邊界較明顯、無社團結構(達到Newman所說的臨界值)。基準網絡節點數量N=200,元數據維度D=2,社團內邊連接概率pin=0.1,生成的網絡指標詳見表3。 表3 基準網絡 3.1.2 基準網絡實驗結果 由于EM算法求解參數最優值時,存在局部極值,因此在本實驗中基于算法多次運行,得到算法平均性能,衡量標準使用準確率和NMI。NMI是用來衡量社團檢測與“真實”情況的方法[18],NMI的值域在0到1之間,如果節點元數據能夠非常準確地預測社團成員,則達到極大值。 1)設置不同網絡參數,本文算法性能對比如圖2所示。 圖2 N=200時各參數下的算法性能 2)本文算法與Newman算法和FN算法的正確率對比如表4所示。 表4 各算法在不同社團質量下的正確率對比 % 為體現算法在真實網絡上的表現,選擇具有真實社團信息并且廣泛使用的Facebook數據集作為算法的驗證網絡。 Facebook數據集來自斯坦福大學(http://snap.stanford.edu/data/),其中包含10個用戶網絡(ego-network),共包含193個朋友圈和4 038位用戶。由于實驗需要真實社團信息,所以,選擇其中具有人工標注的用戶網絡。每個網絡包含一位處于中心的用戶,由用戶標注社團成員(即朋友圈成員),社團數量平均8個,包含不屬于任何社團的用戶 3.2.1 Facebook網絡預處理 通過預處理,提取其中兩位用戶的用戶網絡A和用戶網絡B,其網絡關系如圖3所示,可以看到用戶A的網絡社團結構明顯,用戶B的網絡社團結構不明顯。 圖3 用戶網絡真實社團劃分結果 3.2.2 特征提取 出于對用戶信息安全的考慮,數據集中的用戶特征被映射為對應的值,形成了一個特征矩陣,本文對其做一次主成分分析,并約減到合適的維度。通過實驗發現,用戶網絡A維度為133維、用戶網絡B維度為40時,可以保留原數據的90%的信息。用戶網絡相關參數如表5所示。由模塊度可以看出網絡A比網絡B的社團結構明顯。 表5 用戶網絡參數 3.2.3 真實網絡實驗結果 通常使用BIC準則評價高斯混合模型, 圖4中可以看到,用戶網絡A社團數N=7和用戶網絡B社團數N=6時,bic值達到最小。 圖4 用戶網絡社團劃分的bic值對比 與FN算法得到的社團劃分對比,準確率與NMI對比如表6所示,由于傳統社團檢測算法FN無法比較NMI,因此只能對比社團檢測的準確率。 表6 用戶網絡各算法性能對比 % 3.3.1 基準網絡實驗結果分析 由圖3可以看出,當元數據邊界明顯時,CDNTMN算法性能基本不會受到拓撲結構的影響,準確率穩定在90%以上,隨著社團質量下降,出現了少量的無法收斂的情況。當元數據邊界不明顯時,算法性能隨著社團質量下降而迅速下降,當社團之間邊連接概率大于等于0.06時,算法多次運行的結果中,多次出現無法收斂的情況,同時,社團準確率非常不穩定。 由表4可以看出,本文算法能夠結合節點元數據與拓撲結構檢測社團結構,在復雜網絡中社團結構不明顯時,基于網絡拓撲結構的算法正確率僅有52.5%,而本文算法可以穩定在90%以上。但是當節點元數據分布邊界不明顯,同時社團之間邊連接概率達到Newman定義的條件時,算法性能也會急劇下降。 3.3.2 Facebook網絡實驗結果分析 在Facebook用戶網絡上的實驗可以發現,用戶網絡A的模塊度在0.3左右,節點元數據與社團結構相關程度高,實驗結果較好。用戶網絡B社團結構不明顯,同時節點元數據所標注的社團與算法發現的社團之間存在差異,影響因素是人工采集的特征不完整。 本文算法檢測到的社團與真實社團對比具有如下特點: 1)如果現實世界網絡中社團結構明顯,則任何算法都能夠準確地發現社團結構。 2)如果現實世界網絡中社團結構并不明顯且元數據不能夠反映社團劃分,如用戶網絡B,則本文算法準確率較傳統社團檢測算法有較大的提升。 實驗中發現用戶特征維度各不相同,且用戶特征矩陣為稀疏矩陣,這在一定程度上給用戶特征建模造成一定的困擾。如何確定一個用戶的主要特征,例如,文獻[19]發現雖然在Facebook網絡中。用戶來自世界各個地方的大學,但是一個用戶的朋友網絡中,不同大學數量卻不多,所以,這種具有強烈社團歸屬特性的特征在實驗中沒有重點利用。 本文結合社團檢測算法的現有研究,提出一種基于網絡拓撲結構與節點元數據的社團檢測算法。相比傳統社團檢測算法,該算法在基準網絡中的正確率有顯著提高,結合網絡節點元數據,即使在網絡中社團結構不明顯的情況下,也可以生成較為準確的估計;由于真實網絡的節點元數據維度較高,因此其使用主成分分析約減特征維度,降低了計算復雜度,但是這種特征提取方法仍然比較粗糙,最后的社團檢測結果與人工標注社團有一定相似,不可避免地存在誤差。 本文算法使用的基準網絡具有固定的社團數量且沒有考慮網絡元數據重疊的情況。此外,真實網絡中節點元數據是脫敏映射后的稀疏矩陣,與真正的元數據還具有差距。下一步將針對上述情況做深入研究。1.2 隨機塊模型的改進

2 基于網絡拓撲與節點元數據的社團檢測
2.1 基準網絡似然概率模型建模

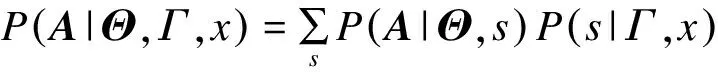
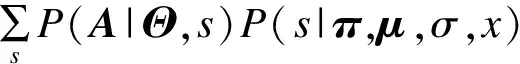
2.2 基于EM算法的推導
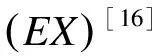
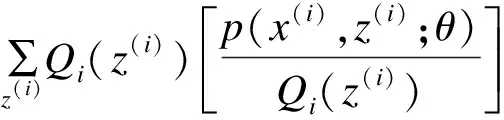
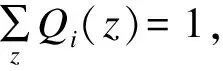
2.3 融合混合高斯模型的似然概率模型求解
3 實驗與結果分析
3.1 基準網絡

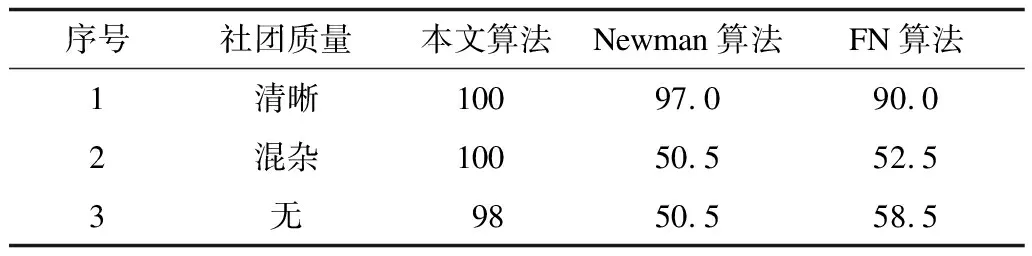
3.2 真實網絡
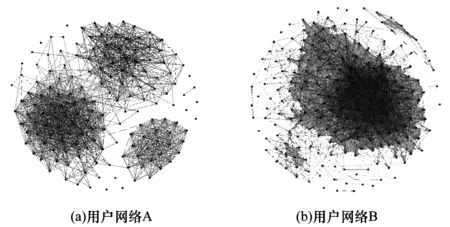

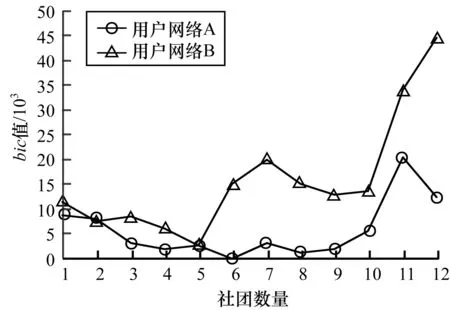
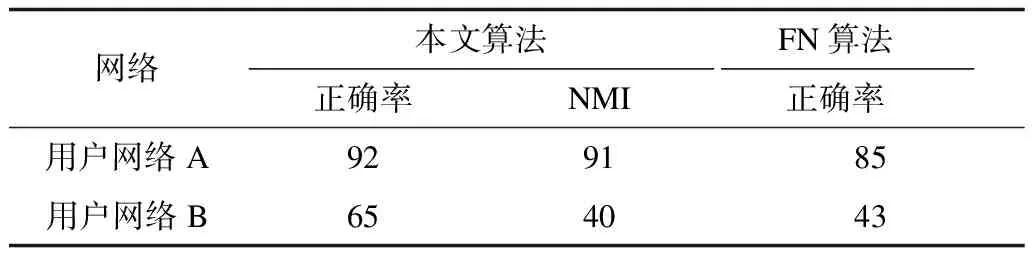
3.3 結果分析
4 結束語

