一種基于結構特征的樹相似度計算方法
陳彥樺,李 劍
(北京郵電大學 計算機學院,北京 100876)
0 概述
隨著計算機技術和Internet的迅速普及,人們正在進入一個信息爆炸時代。伴隨著海量數據急劇增加,迅速產生和積累了大量的結構化與半結構化數據,而對于這些數據,圖挖掘算法的研究逐漸興起并得到重視。樹作為圖的特殊表達形式,也有較為重要的研究意義。
在計算樹的相似度方面,現已出現較多的研究。自文獻[1]提出編輯距離算法后,研究者不斷地對該算法進行改進。文獻[2]提出基于樹編輯距離的層次聚類算法,將樹的編輯距離定義為d(T,T’)=min{r(P)|P是將T轉化為T’的一系列樹編輯操作},這些編輯操作包括插入、刪除、轉換節點。計算樹的編輯距離就是求使T轉化為T’所需樹編輯操作的最少次數。因此,可以利用樹的編輯距離計算樹的相似度。每次計算時間復雜度為p×q×l2×l'2(樹T、T’的長度分別為p、q,最大深度分別為l、l’),這是一個多項式的時間復雜度。
近年來,關于樹的編輯距離有不少拓展的研究。文獻[3]分析了基于無序樹編輯距離的結構敏感變化問題。文獻[4]提出了RTED算法,即一種魯棒性的樹編輯距離算法,解決了有序標記樹的編輯距離問題。文獻[5]展示了最大協議子樹(MAST)問題和樹編輯距離之間的關系。文獻[6]對原本處理字符串編輯距離的GESL算法進行了擴展,將其應用到樹的編輯距離中,在樹的相似度計算上發揮了巨大的作用。文獻[7]主要處理有序標記樹的XML文檔。該文指出常規的樹編輯距離缺乏靈活性和效率,并提出了2個新的編輯操作,對原算法做了擴展,在與分層數據結構的相似性匹配上達到了良好的性能。文獻[8]指出被廣泛應用的RTED算法消耗內存過多,提出了一種新的樹編輯距離算法AP-TED,該算法在時間性能上和RTED相當,并大幅減小了內存的使用。文獻[9]主要研究無序的、有唯一標記的樹。該文將編輯距離的原子操作定義為“局部移動”,并提出了一種新的樹編輯距離算法SuMoTED,這是一種新的度量方法,定義為將一棵樹轉換為另一棵樹所需的“局部移動”的最小數量,具有二次時間復雜度。文獻[10]提出了一種基于映射的匹配算法,預先得出2棵本體樹的節點之間的相似度,然后使用基于編輯操作的映射理論將2棵樹轉換成同構樹,最終得到2個本體之間的最大相似度和最佳匹配對。文獻[11]將網頁評論的識別與自動提取轉化為DOM樹結構中的子樹循環體識別問題,提出一種基于網頁DOM子樹相似度計算的方法,從網頁中〈BODY〉節點向下逐層遍歷識別出滿足約定條件的評論塊節點樹。文獻[12]提出一種基于加權頻繁子樹相似度的網頁評論信息抽取方法WTS。首先通過視覺特征對網頁進行剪枝處理;然后利用深度加權的相似度度量方法抽取最佳頻繁子樹;最后通過子樹對齊方法抽取評論路徑并解析評論內容。
上述算法共同之處在于都是直接計算樹的相似度,但如果樹的規模較大,那么聚類將是一項很費時的工作。受文獻[13]的啟發,本文提出基于樹結構特征計算相似度的方法,構造出K個節點的所有非同構形態的子樹,并計算這些子樹的同構個數,將其作為特征向量來進行樹的相似度計算。
1 樹和樹的同構
樹是由n(n≥0)個節點構成的有限集。可由如下遞歸方式定義一棵樹:
1)在任意一棵非空樹中,有且僅有一個特定的稱為根的節點。
2)當n>1時,其余節點可分為m(m≥0)個互不相交的有限集T1,T2,…,Tm,其中每一個集合本身又是一棵樹,并且T1,T2,…,Tm稱為根的子樹。
樹又可分為有序樹和無序樹。顧名思義,有序樹即孩子節點之間存在確定的次序關系,無序樹則相反。本文的研究是基于無序樹展開的,如無特別說明,下面提及的樹都是指無序樹。
樹是圖的特殊表現形式,因此,也可以用圖的定義來描述一棵樹。
定義1(樹) 令LV和LE分別是節點和邊的有窮或無窮字母集合,樹t是一個滿足下列條件的四元組t=(V,E,u,v):
1)V是有限的頂點集;
2)E∈V×V是邊集;
3)u:V→LV是頂點屬性映射函數;
4)v:E→LE是邊屬性映射函數;
5)根節點入度為0,其余節點入度為1。
以樹的定義為基礎,下面給出子樹的定義。
定義2(子樹) 令t1=(V1,E1,u1,v1),t2=(V2,E2,u2,v2),t1是t2的子樹,表示為t1∈t2,當且僅當下列條件成立:
1)V1∈V2;
2)E1∈E2;
3)對任意u∈V1,存在u1(u)=u2(u);
4)對任意e∈E1,存在v1(e)=v2(e)。
樹t1和t2的一致性,通常需要由一個映射函數來建立,將樹t1映射到樹t2上,即樹的同構。
定義3(樹的同構) 令t1=(V1,E1,u1,v1),t2=(V2,E2,u2,v2),樹的同構是一個雙射,f:V1?V2,當且僅當下列條件成立:
1)對任意u∈V1,存在u1(u)=u2(f(u));
2)對任意e1=(u,v)∈E1,存在邊e2=(f(u),f(v))∈E2且v1(e1)=v2(e2);
3)對任意e2=(u,v)∈E2,存在邊e1=(f(u),f(v))∈E1且v1(e2)=v2(e1)。
兩棵樹同構,要求它們的屬性和結構上具有完全的一致性,即對于第一棵樹的每一個節點和第二棵樹的每一個節點之間具有一對一的對應關系,同時保證邊結構保留完整,以及節點和邊的屬性一致。本文主要著眼于樹的結構,對樹節點和邊的屬性沒有涉及,弱化了樹的同構的定義,只考慮樹的節點間一對一的對應關系和邊結構的完整性,未考慮節點和邊的屬性一致。
定義4(子樹同構) 令t1=(V1,E1,u1,v1),t2=(V2,E2,u2,v2),從t1到t2的一個單射f:V1→V2稱為子樹同構,當且僅當存在子樹t∈t2使得f是t與t1的一個同構。
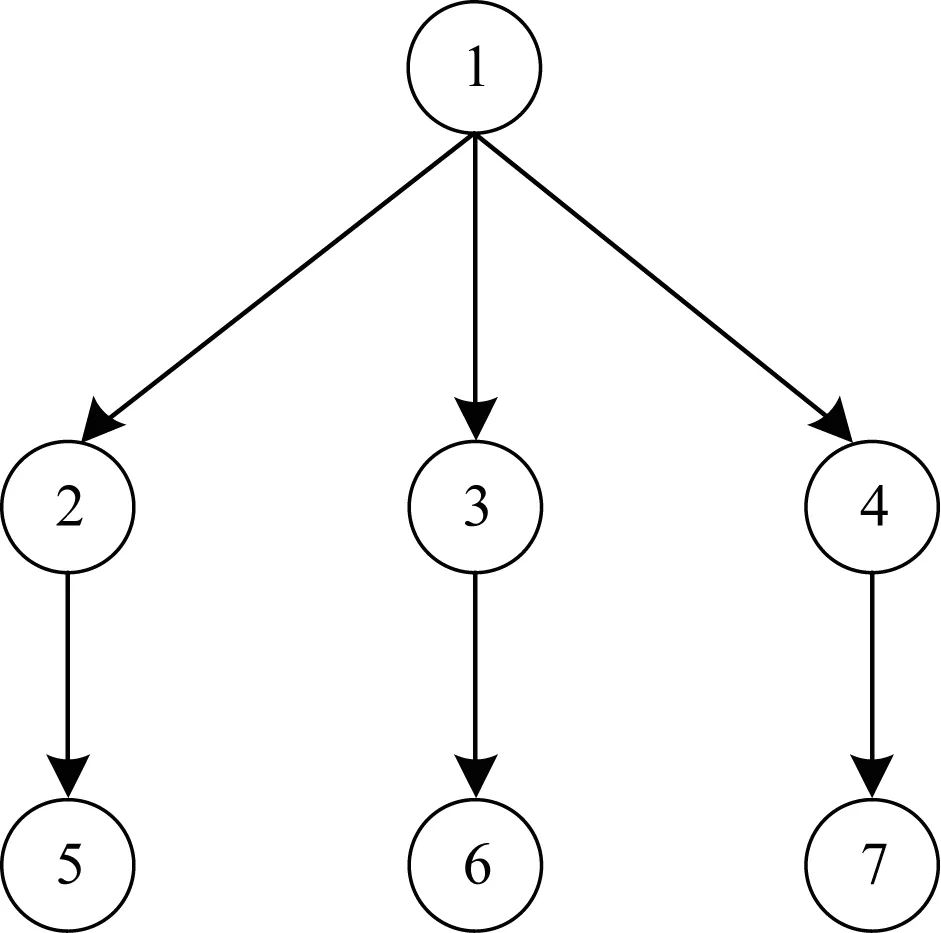
根據子樹同構的定義,本文提出子樹同構個數的概念,即求從t1到t2的單射f:V1→V2的個數。

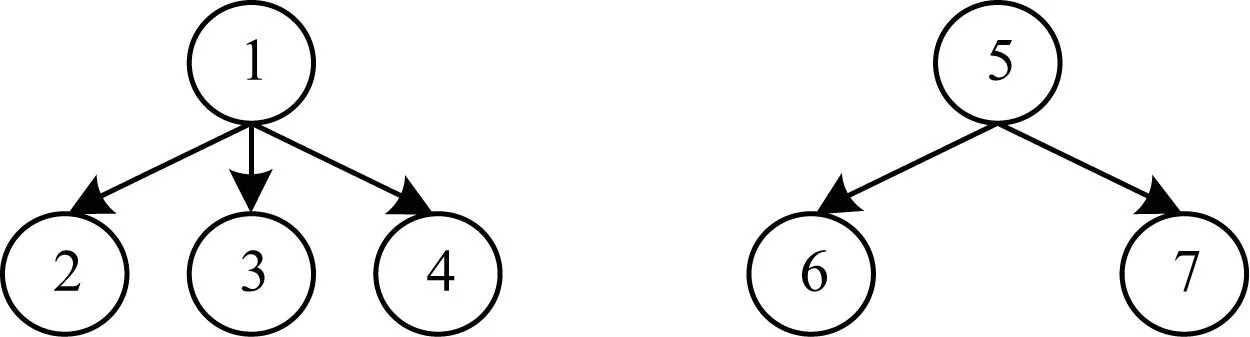
圖1 子樹同構個數示例
2 樹的相似度計算
本文采取的是提取樹特征的方式進行樹的相似度計算。首先枚舉出所有K子樹tK(節點數為K)的非同構形態如圖2所示,設tK個數為m,而需要進行特征提取的樹記為T。
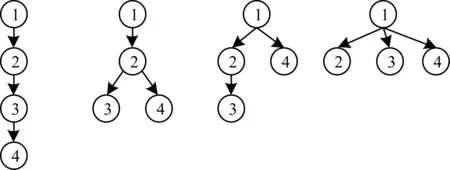
圖2 K=4時tK的4種非同構形態
算法需要計算在T中tK1~tKm所有子樹的同構個數,而這些計數則可構成T的特征向量A。進行樹的相似度計算和聚類都可以用A進行。下面將介紹樹的構建和tK在T中同構子樹個數的計算方法。
2.1 同構子樹算法
設tK的根節點為RtK,則本文需要將RtK和T中所有的節點進行比較,將每一次計算出來的同構個數進行累加,最后累加的結果就是tK在T中的同構子樹個數。而每一次根節點之間的比較又可分為兩部分的乘積:一部分是RtK的葉子節點和RT的孩子節點的對應結果,另一部分是RtK的非葉子孩子結點和RT的非葉子孩子結點的對應結果。T中某一節點RT和tK的根節點RtK的比較過程如下:
輸入T中某一節點RT和tK的根節點RtK
輸出RtK在RT中的同構子樹個數
IsoSubtCnt(RT,RtK)
Begin
1.DT=RT的出度;
2.DtK=RtK的出度;
3.DT0K=RT中為葉子節點的孩子節點個數;
4.Dt0K=RtK中為葉子節點的孩子節點個數;
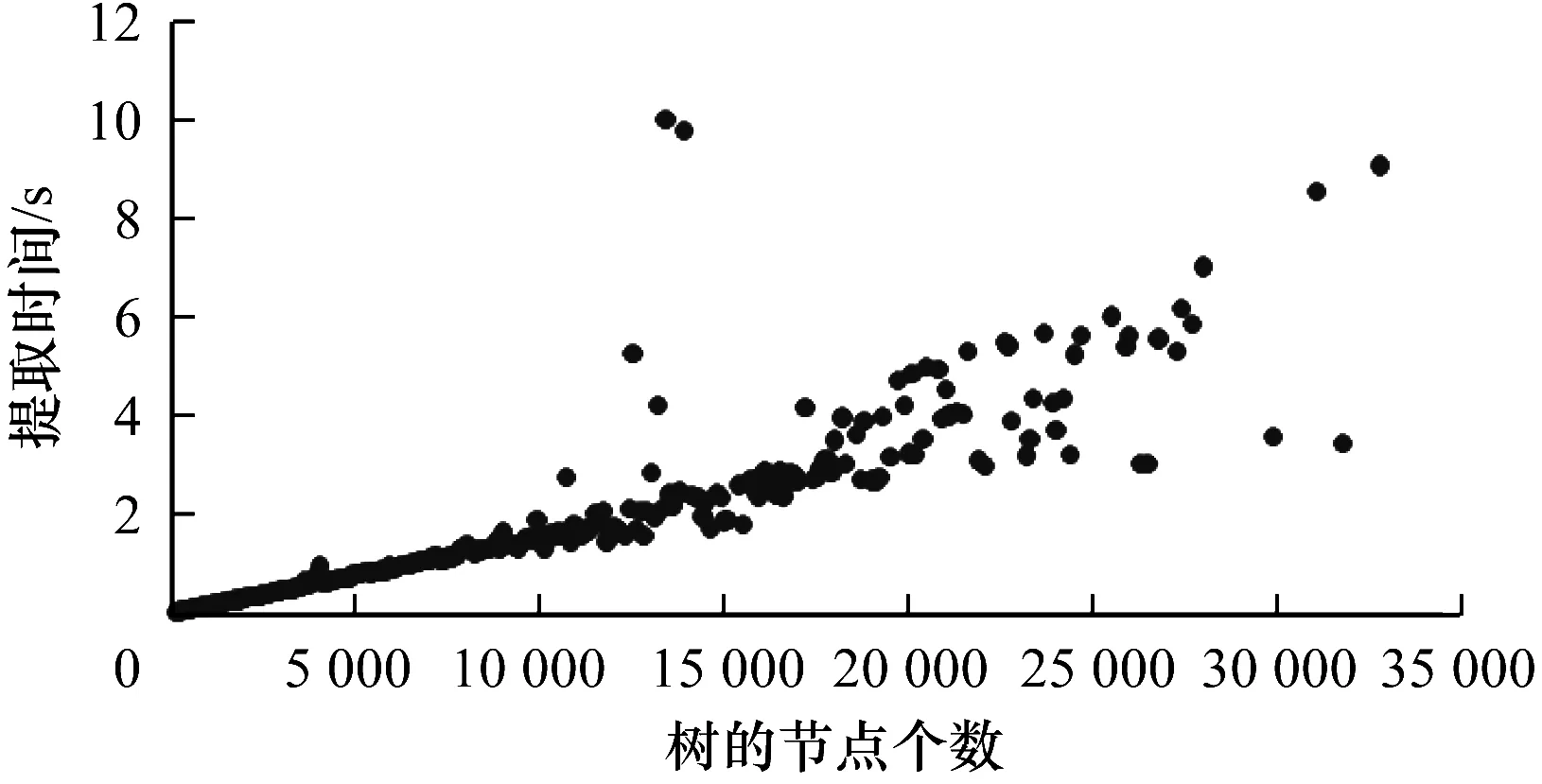
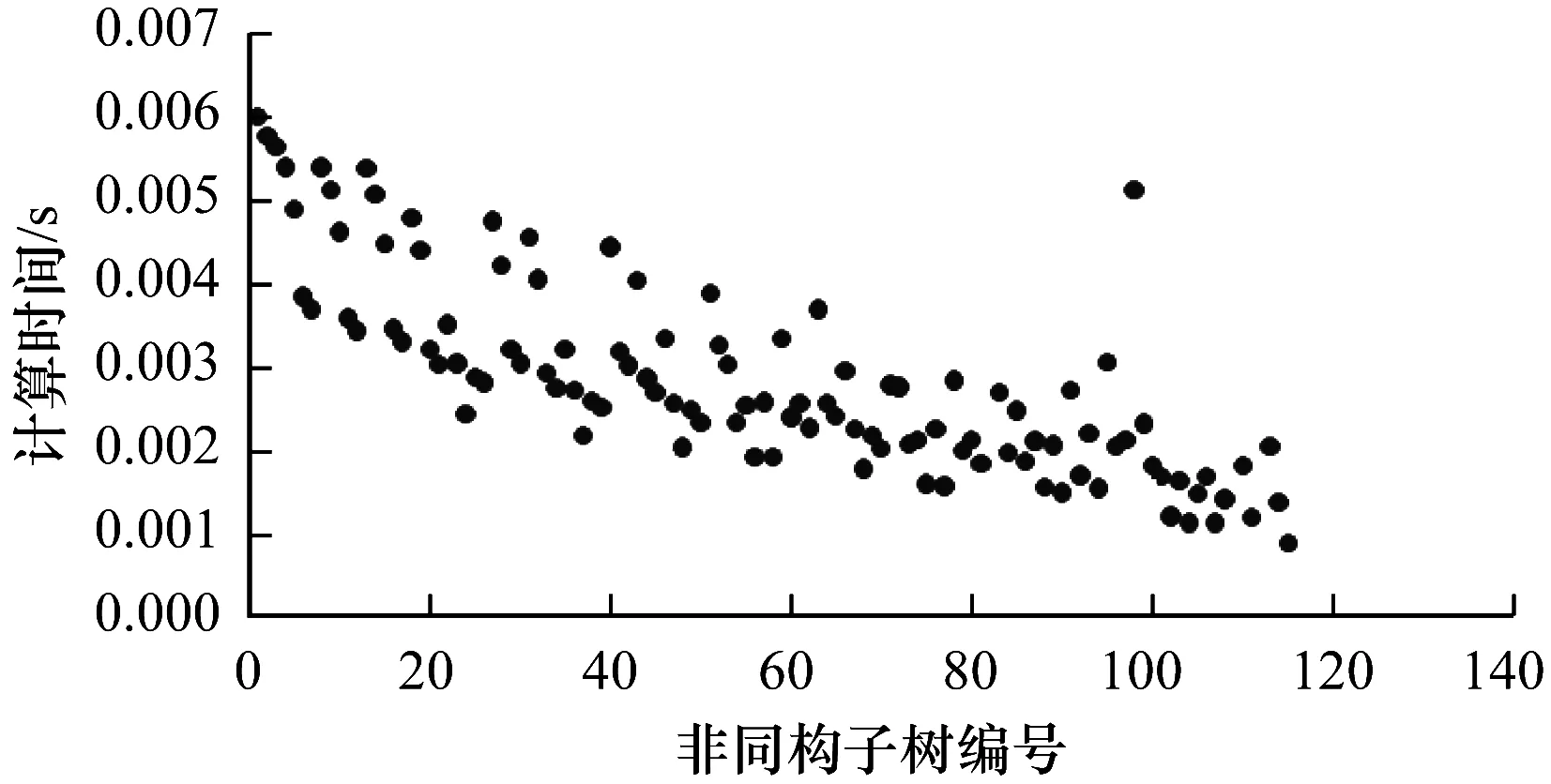
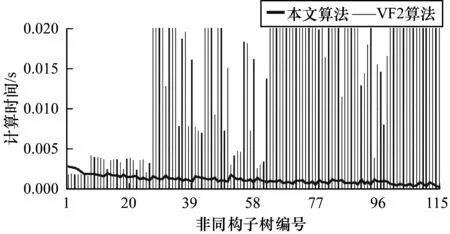
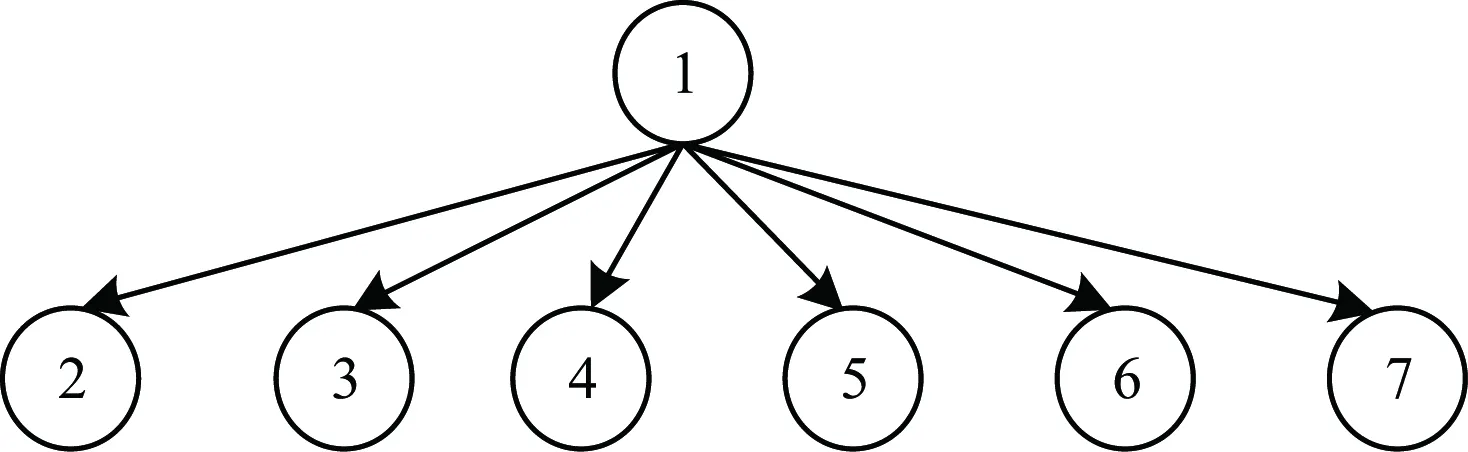
5.IFDT 6.RETURN 0; 8.I=DtK-Dt0K; 9.J=DT-DT0K; 10.TmpPart2[I][J] = {0}; 11.FOR i from 1 to I: 12.FOR j from 1 to J: 13.TmpPart2[i][j]=IsoSubCnt(RTi,RtKj); 14.END FOR j; 15.END FOR i; 16.ResultPart2=Comb(TmpPart2,I,J); 17.RETURN ResultPart1*ResultPart2; 輸入TmpPart2 輸出RT和RtK的所有非葉子孩子結點的對應關系個數 Comb(TmpPart2,I,J) 1.Val=0; 2.First=TmpPart2[0][],記錄第0行; 3.delete TmpPart2[0][],刪除第0行; 4.FOR j from 1 to J: 5.delete TmpPart2[][j],刪除第j列; 6.Val += First[j] *Comb(TmpPart2,I-1,J-1); 7.restore TmpPart2[][j],恢復第j列; 8.END FOR j; 9.RETURN Val; End 由上述比較過程可知,RtK在RT中同構子樹的數目由RtK的葉子節點和非葉子孩子結點在RT中的對應關系組合而成。而葉子節點的計算不需要2棵樹葉子節點的一一對應,只需計算RT中能夠提供給RtK葉子節點匹配的數目,從中選出Dt0K個并進行全排列即可;非葉子結點孩子的計算則需要2棵樹非葉子結點的一一對應,并進行組合。 在同構子樹個數的計算過程中,設RT和RtK比較時間復雜度為TC(RT,RtK),RT的非葉子孩子結點數為m,RtK的非葉子孩子結點數為n,則: (1) TCh=XTh-1+Y (2) 根據上述同構子樹個數計算算法,可以得到一組關于T的特征向量,利用其進行樹的相似度計算。根據實驗的數據屬性,可以采用不同的計算相似度的方法。根據本次實驗的數據特征,每一棵子樹同構數目差別較大,因此,采用式(3)定義向量間的相似度。 (3) 其中,A、B為2組特征向量,長度為n,Ai、Bi代表特征向量第i維的值,min(Ai,Bi)為Ai、Bi中較小的一個的值,max(Ai,Bi)則相反。 本文采用的實驗數據來自安卓應用市場下載的23 529個安卓APK文件。這些安卓應用是分家族的,也就是一個應用有多個版本。經過反匯編后得到應用程序的函數結構調用圖,并將其轉換成樹的形式。本文的實驗目的是測試算法在實際數據上的性能,并驗證相似度高的2個應用為同一家族。 經過對實驗數據的預處理,得到的信息如表1和表2所示。 表1 23 529棵樹的節點出度 表2 23 529棵樹的節點個數 本文取K=8,記錄下每一棵樹提取特征所需時間,并記錄下計算每一種子樹形態tK所需時間。K=8時,共有115種非同構子樹形態,如圖3和圖4所示。在圖3中,有5組數據沒有在圖中展示,分別為:14 600~14 700時的94.6;18 000~18 100時的233.5;19 500~19 600時的120.6;19 700~19 800時的158.9;20 500~20 600時的160.1。在圖4中,有3組數據沒有在圖中展示,分別為:82時的0.040 0;109時的0.037 8;112時的0.039 6。 圖3 樹節點個數與特征提取時間的關系 圖4 不同形態子樹的計算時間 圖5 編號為82、109、112的子樹共同包含的結構 為比較算法性能的優劣,本文選擇了開源工具igraph來計算同構子樹的個數。在igraph中有提供函數igraph_count_subisomorphisms_vf2,即用VF[14]算法演變而來的VF2算法[15]來計算同構子樹的個數。VF2算法是目前較為優秀的同構子圖計算算法之一,是VF算法的擴展,與同類算法相比,有較優的時間復雜度和空間復雜度。由于目前并沒有子樹同構個數計算算法,因此本文將VF2算法作為比對算法,檢驗本文算法的性能提升。由于VF2算法在某些情況下計算時間太長,因此本文只挑選了1組數據進行計算。該組數據有513個節點,最大節點出度為53。實驗結果如圖6所示。 圖6 本文算法與VF2算法的時間性能比較 由圖6可以看出,VF2算法計算115棵同構子樹的個數花費時間為3 430 s,而本文算法花費時間0.132 8 s,VF2算法中93.9%的子樹運行時間遠在本文算法之上。在VF2算法花費時間較長的子樹的特征中,最明顯的就是115號子樹,如圖7所示。 圖7 編號為115的子樹形態 這些子樹的共同特征是具有較多的葉子節點,而樹T中一些節點出度較大。VF2算法需要枚舉出所有的葉子節點的映射關系,導致了算法運行時間增大。可以看出本文算法在子樹同一層葉子節點較多的情況下優勢明顯。 本文按照式(3)對23 529個特征向量進行了相似度計算。這些特征向量分屬6 799個類別,即有6 799類安卓家族程序。相似度比較結果如表3和表4所示。 表3 6 799類安卓家族程序族內相似度比較 表4 23 529個安卓程序族間相似度比較 由表3可以看出,在6 799個家族中,相似度較高的家族程序所占比例較大,相似度在0.7以上的占比達74%。本文查看了相似度較低的家族程序提取的特征向量,發現它們的差距確實比較大;而實際安裝這些不同版本的同家族程序,發現它們之間的改動比較明顯。而由表4可以看出,不同類別的安卓程序相似度都比較低,不超過0.2。這一方面說明同家族的程序相似度較大,不同家族的程序相似度較小,而本文提取的特征向量能較好地反映程序間的相似度;另一方面顯示出某些家族程序改版較大,這也符合實際情況。 現階段,不少學者對樹的相似度計算都是通過直接比較兩棵樹的特征進行的,但是都不能很好地處理數據量較大的情況。本文基于文獻[13]的研究,通過樹的結構特征來進行樹的相似度計算。實驗結果顯示:隨著樹規模的增大,算法時間復雜度并不是呈指數增大,而是線性增大,這說明本文算法能夠適用于規模較大的數據;在相似度計算方面,同類家族的程序相似度較高,相似度在0.7以上的家族程序占比達74%;不同類家族的程序相似度較低,相似度不超過0.2,這也說明了程序的相似度可以用提取的特征向量的相似度來表示,而有的家族程序的相似度較低,說明這類程序在某一版本之后做了較大的改動,導致程序結構調用圖有了較大的變化。上述結果均表明提取的特征向量能高效準確地用于樹的相似度計算。下一步將研究本文算法在惡意軟件檢測、網頁結構特征抽取等場景應用的情況,同時提高算法的實用性。
2.2 同構子樹算法的時間復雜度
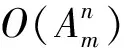
2.3 樹相似度算法
3 實驗與結果分析
3.1 實驗數據

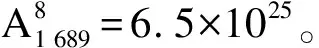
3.2 特征向量提取
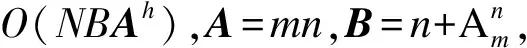
3.3 相似度比較


4 結束語

