小問題,大智慧
梁燕


我們從一個小問題說起.
問題 解方程:(1) sinx+√3 cosx=O; 2) sinx+√3 cosx=1
一、發現特性,多方切入
對于這個問題,文墨、宇軒、思遠三個好朋友進行了一番熱烈的討論,苦思冥想仍存在些許疑惑,于是找到了老師.
文墨:式子(1)左右兩邊同除以COSx,轉化為一個函數名,得tanx√3=o.
宇軒:你的方法對齊次式是可行的,對非齊次式不可行.如(2)式,同除以COS z后會出現1/cosx與tanx,不能達到消元的目的.因此這個方法不具備一般性.
宇軒:對于式子(2),既然是關于sin x與COSx的方程,我想到了同角三角函數關系公式,可以聯立方程組,通過解方程組求出sinx與COS x
思遠:宇軒的方法具有一般性,可是解方程組計算量大,我有更簡單的方法.化簡等式左邊,sinx+√3cosx=2(1/2sinx+√3cosx/2)=2(sinx cOsπ、3+COS xinπ/3)一2sin(x+π/3),方程即為2sin(x+π/3)=1,sin(x+π/3)=1/2,從而可得解.
文墨:厲害!首先“乘2除2”構造特殊角三角函數值,再逆用兩角和的正弦公式化為和角的三角函數式.你是怎么想到“乘2除2”的呢?
思遠:觀察等式,聯想到剛學過的兩角和的正弦公式sin(x+y) = sin xcosy+COSxsin y,發現sinx+√3cosx與公式右邊的結構相似,公式中sin x與COS x前面的系數分別是cosy和siny,兩者平方和為1,而“1”與“√3”不滿足要求,但如果是“1/2”與“√3/2”就可以實現公式的逆用,于是我提取2.
宇軒:原來是兩角和與差的正弦公式的逆向變形,看來以后要學會逆向思維.不過剛才的“1”與‘√3”比較特殊,可以湊出平方和為1,那3cosx+4sinx怎么辦?形如asin0 +bcos0,是否都可以寫成y =Asin(ωx+ψ的形式呢?
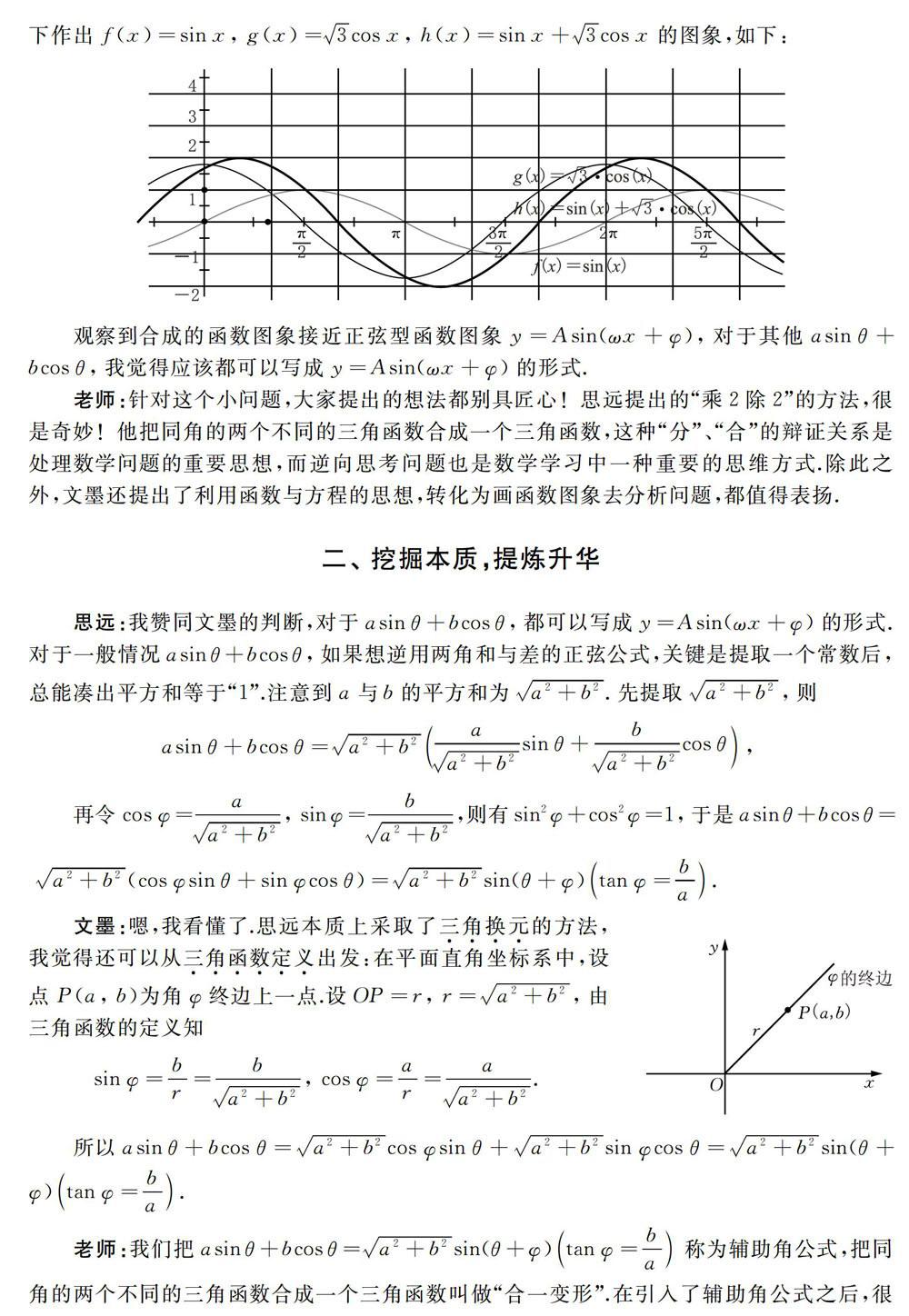
文墨:解方程問題可以轉化為函數問題,對于特殊情形,我借助幾何畫板,在同一坐標系下作出f( x)=sinx,g(x) =√3cosx.h(x)=sinx+√3cos x的圖象,如下:
觀察到合成的函數圖象接近正弦型函數圖象y=A sin(ωx+ψ),對于其他asin臼+bcosθ,我覺得應該都可以寫成y=Asin(ωx+ψ的形式,
老師:針對這個小問題,大家提出的想法都別具匠心!思遠提出的“乘2除2”的方法,很是奇妙!他把同角的兩個不同的三角函數合成一個三角函數,這種“分”、“合”的辯證關系是處理數學問題的重要思想,而逆向思考問題也是數學學習中一種重要的思維方式.除此之外,文墨還提出了利用函數與方程的思想,轉化為畫函數圖象去分析問題,都值得表揚,
二、挖掘本質,提煉升華
三、靈活運用,鞏固提升
點評
輔助角公式的目的在于將三角式化為一個三角函數的形式,由此可以展開對三角式相關性質的研究,比如單調性、周期性、有界性,它在解決問題時起到一個重要的橋梁作用,它是我們解決與三角有關的函數問題的重要變換手段.輔助角公式的目的是化簡三角函數式,在實際中結果是化正弦還是余弦要具體問題具體分析,不必拘于結論的形式,搭配好對應的三角函數公式.如該題還可以化簡為f(x)=-2cos (2x+π/6)+√3-1.
“輔助角公式”能夠合二為一,解決了不少三角函數問題.所謂“二合一”,就是利用輔助角公式把同角的兩個不同的三角函數“合成”一個三角函數.其本質的特征就是通過轉化,化為一個三角函數,再根據換元法,轉化為基本三角函數問題,為進一步研究其性質(周期性、對稱性、單調性、值域)打下基礎.大家可不能小瞧它的作用!
鞏固練習
1.已知2cos2x +sin 2x =A sin(ωx+ψ)+b(A>0),則A=_____,b=_____.
2.函數y=sinx-√3cosx圖象可由函數y=2sinx的圖象至少向右平移______個單位長度得到.
參考答案
1.√2,1. 2.π/3

