從必要性、合理性視角下談數學概念的教學策略

楊智勇

（廣州市從化區第四中學，廣東 廣州）

數學概念是客觀現象的數量關系和空間形式的本質屬性的反映，是人類認識事物的智慧結晶，是思維的基本單位。它起始于問題，最終又幫助人們以此為據點去認識解決新的問題，是數學教學的重中之重。但常因其抽象的學科特征總給人以冰冷的感覺。積累數學活動體驗，經歷概念的發現、發展、生成、再創造過程，以具體的經驗作為支撐，那么教師應如何幫學生打開數學概念這扇知識寶殿的大門呢？一是學生要有進門的欲望，二是學生要有合情合理的進門途徑。即教師應解決概念學習的必要性和學習探究過程合理性的問題，追求自然生成的概念教學。下面筆者就概念的情景引入、數學建構談一點體會。

一、情景引入——體現數學概念學習的必要性

疑為思之源，思為智之本。學習接觸一個新事物，要激發學習者強烈的求知欲望，莫過于讓學生產生疑惑或強烈的認知沖突。所以對于概念的教學首先應解決概念學習必要性的問題，即為什么要學。在學習充要條件時，筆者以學生中段考試題中錯誤的解法以案例的形式展示出來。要求學生指出錯誤，并深入分析錯因。

觀察案例：若關于x的不等式kx2+kx+2>0的解集為R，求k的取值范圍？

解：∵kx2+kx+2>0的解集為R，

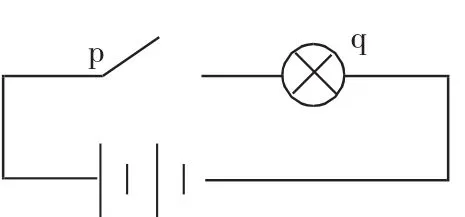
當k>0時，由二次函數的圖像可知此時有：Δ=b2-4ac=k2-8k<0，解得k的范圍為0

當k<0時，由二次函數的圖像可知此時不存在這樣的k滿足題意。

綜上所述，k的取值范圍是｛k|0

生1：還有k=0時，此時2>0恒成立。所以綜上所述，k的取值范圍是｛k|0≤k<4｝。

師：為什么會犯這樣的錯？

生2：因為把它當作一元二次不等式來處理。沒有考慮k=0的情況。

師：觀察這個不等式，我們用定式思維去思考問題，犯了邏輯上的錯誤。如何厘清問題的條件、結論之間的邏輯關系？盡量少或不犯這樣的錯誤，這就是我們今天要學習的課題。

溫故而知新。以學生答卷中存在的典型問題切入，既讓學生感到熟悉親切，引起共鳴，又能激發對新知的探究欲望，同時教師以為什么錯進一步引導學生分析錯因，最大限度發揮錯誤的價值，為學習新知創設了情景。又如在學習分類相加、分步相乘的計數原理時，我從學生生活中的案例入手：若你不慎遺失銀行卡或存折，你會擔心別人撿到你的卡或存折，從而把你的錢取走嗎？你能從數學“量”的角度做到以理服人嗎？讓學生產生“惑”，既引起學生學習的興趣，又激發學生探索新知的欲望。數學概念一般具有豐富的現實原型，引入應更自然、更貼切生活。

二、數學建構——體現概念獲得的合理性

數學代表著理性，學生在數學概念學習、探究、生成、再創造過程中，在知識呈現上、問題設置上、思維發展上應體現合理性。

學習概念新知的過程中，知識呈現上的合理性主要體現在以下幾方面：

①知識產生的背景或情景應該是學生熟悉的，既能激發學習興趣，又能跳一跳摘到果子。切忌晦澀、深奧，一開始就給學生一個下馬威。如在“充要條件”概念獲取中，筆者以學生自己所在的班級作為問題的背景：

情景問題：把下列命題寫成“若p則q”的形式，并判斷真假。你能用集合的韋恩圖表示這種邏輯關系嗎？

命題 p：趙××是從化四中高二（2）班的學生；命題 q：趙××是從化四中高二級的學生。

命題 p：x≥5；命題 q：x≥1。

②所呈現的知識應該是符合學生認知的。如在學習函數零點時不應該涉及連續函數這個未知概念，只能從直觀圖像：一條連續不斷的曲線入手。又如筆者在p?q可知p是q的充分條件，但同時q是p的必要條件。本課的難點如何突破呢？從“無之必不行”入手，必要性是無“之”必不行。故由命題若p則q寫出若﹁p則﹁q，并判斷它們的真假來突破必要性的難點，但是卻生生割裂了教材，不符合學生的認知規律及知識的連貫性、系統性，決定由原命題及其逆否命題若﹁q則﹁p來設計教學。聯系剛接觸的四種命題，以原命題的逆否命題入手來探討q對于p的必要性，順應學生的認知規律。

③所呈現的知識應該凸顯學生對概念全面的認識、深刻的理解。盲人摸象永遠無法了解事物的真相和全部，如認為y=ax2+bx+c就是二次函數。不識廬山真面目，只緣身在此山中。在概念的學習中，應有意識凸顯概念的內涵與外延，概念的內涵應通過大量的事例來分析、比較、歸納、抽象出概念的本質屬性，揭示概念與它的逆命題都是真命題。由新概念聯想、拓展、應用到已有的與之相關的具體知識，體現由具體到一般、又由一般到具體的認識過程；應有意識從反例強化，加深對概念的甄別；應有意識從數量關系、空間形式或改變概念的某些本質屬性等多角度來認識概念；應有意識從不同角度給概念下其他可能的定義。

問題是數學的核心，是知識的載體，是學習動因的第一驅動力。陶行知則說：“發明千千萬，起點在一問。”以問題驅動概念新知的學習，如何“問”同樣顯得舉足輕重。

①有效的問題設計應基于學生的認知水平，著力于學生的知識、能力、思維的生長點。筆者在“充要條件”中介紹了p?q可知p是q的充分條件，同時q是p的必要條件后，基于學生認知，進行鞏固訓練，著力于知識生長點及時進行應用，同時生成新知充分必要條件。設計了一組題組：

Ⅰ下列“若p則q”的命題中，哪些命題中的p是q的充分條件？

（1）若 x=1，則 x2-4x+3=0；

（2）若兩直線平行，則這兩條直線的斜率相等。

Ⅱ如圖1：p：開關閉合，

圖1

q：燈泡亮；觀察p和q之間有怎樣的邏輯關系？

Ⅲ你能找到兩個命題之間類似的邏輯關系嗎？

Ⅳ你能用集合的韋恩圖表示這種關系嗎？

基于學生的認知水平，在學生的最近發展區設計問題，能引起學生的共鳴，激發學習的興趣，提升教學效能；反之，若離開學生的認知水平設計問題，就不能有效調動學生的積極性，課堂表現為人人都不開口，被動接受知識，學生沒有參與課堂，沒有思維活動，也就談不上對概念的準確、深刻理解、掌握。

②問題設計應盡量多一點變式、多一次追問，凸顯概念在學生心中從“有”到“更有”的精致過程。題海無涯，反思是岸。課堂教學是學生學好數學的主陣地，要實現高效教學，教師必須最大限度地挖掘問題的作用，使數學概念經歷從日常語言到樸素的數學語言到圖形語言再到數字化符號的階段，使學生經歷從概念的生成、發展、建構再到應用的過程。筆者在“計數原理”設計了如下問題串：

情景問題1：如果用一個大寫的英文字母或一個阿拉伯數字給從化的景區編號，那么總共能夠編出多少種不同的號碼？

變式一：用一個大寫英文字母和1～9九個阿拉伯數字，以A1，A2，···，B1，B2，···的方式給從化景區編號，總共能編出多少種不同的號碼？

追問二：以上兩個計數問題的結果相同嗎？為什么不同或者說是什么導致了它們的不同？

追問三：從化景區有4個較大的溫泉休閑點，3條綠道，2個國家森林公園，一旅行團來從化旅游。

（1）從以上景點中任取一處，有多少種不同的取法？

（2）從三類旅游景點中各取一處，有多少種不同取法？

（3）從三類旅游景點取2處不同種類的景點，有多少種不同的取法？

筆者結合身邊景點的具體實例，通過變式一、追問二讓學生通過列樹狀圖經歷兩個計數原理的抽象、概括、發現過程，通過追問三體驗兩個計數原理的聯系與區別，幫助學生從整體上把握。概念教學在設置問題時不應是一座座“獨木橋”，而是錯綜復雜的“立交橋”。如何引導學生看清它從哪里來，可以怎么走？還能延伸到哪里去？而變式和追問能引導學生構建良好的知識結構，進而使學生由知識到技能，最終形成能力。

數學是一門思維的科學，而數學概念恰是前人大量智慧的結晶。學生經歷概念的發現、發展、生成、再創造過程，就是思維不斷提升的過程，應是春風化雨、潤物無聲的過程。

Ⅰ教學內容避免瑣碎、零亂；教學環節避免機械和重復；教學方式避免把概念課上成例題與習題講解課，從而構建脈絡清晰、主次分明、綱舉目張的課堂結構。簡潔、順暢、自然。既遵循思維的本質特征，又符合學生的心理需求，從而使學生的思維得到很好的發展和提升。如筆者在“充分條件與必要條件”概念教學中制定如下的教學流程：

Ⅱ數學思維的發展要遵循人們心理認知的規律。心理學告訴我們人們認識新事物是一個螺旋式上升、反復加深的過程，也是思維不斷深化、品質不斷提升的非線性過程。它是一個長期的過程，絕不能畢其功于一堂課。這就要求我們設計課堂教學內容時要懂得選擇、取舍、整合，不能全面開花、全線出擊。教師應居高臨下，站在系統的角度，根據學生的認知水平來決定哪些該取，哪些該舍，哪些可以現在取，哪些應該先舍后再取。如在教學指數函數時，課本中用的分別是細胞分裂和放射性物質衰變，例子雖好但與學生的認知有一定距離，可舍。教師可以請同學們拿出一張普通的紙設置問題：（1）對折次數、紙的層數的關系是什么？（2）設紙的面積為1，則紙的面積與對折次數的關系？直觀具體有操作性。然后進一步追問這兩個函數有什么異同，從而歸納出指數函數的概念。再從概念的內涵、外延著力從正反兩個角度及變形問題，夯實學生對指數函數的理解、把握。以上的教學設計對課本中的案例“舍”，對函數的圖像、性質“舍”，對指數函數的概念及其本質特征“取”，對概念的簡單應用“取”。整節課自然、流暢、重點突出、脈絡清晰，符合學生在體驗中獲取經驗，不斷反思、修正、精致、提升，最后形成抽象概念，并適當應用的心理認知規律。

李邦河院士曾說：“數學是玩概念的。”尤其在素質教育、新課標、新高考的背景下，我們只有充分重視概念的教學，著力讓學生體驗數學概念的再生成、再創造的過程，才能真正夯實學生對抽象數學概念的理解、掌握，才能構建良好的知識體系，才能主動、快速檢索到相關知識解決問題，才能著力提高學生解決問題的能力。