非對稱載荷下驅動軸強度與剛度的匹配與優化

王佳羽，鄭松林,2，趙禮輝,2，馮金芝,2

（1. 上海理工大學 機械工程學院，上海 200093；2. 上海理工大學 機械工業汽車底盤機械零部件強度與可靠性評價重點實驗室，上海 200093）

驅動軸是特種車輛傳動裝置的關鍵零部件之一，其設計約束條件多，指標實現困難，且驅動軸的疲勞壽命往往直接決定了車輛的有效使用壽命[1-3]。為此，常采用超高強度合金結構鋼作為驅動軸的優選材料。然而，由于驅動軸的工作環境較為惡劣，承受的載荷復雜多變，尤其是換擋時的沖擊載荷引起的損傷較大，導致驅動軸極易發生低周疲勞失效，嚴重影響整車功能的發揮。非對稱載荷是指驅動軸受安裝設計條件限制，兩側輸出端通常聯接不同的零/部件，左右花鍵受力不一致，導致驅動軸兩側分配的載荷為不對稱載荷，對軸的疲勞壽命影響較大。對于這類承載軸的疲勞失效，許多學者進行過專題研究。姜濤等[4]對某特種車輛主傳動軸的疲勞斷裂進行分析，確定了工作中存在的扭振載荷和齒根圓角偏小導致傳動軸提前失效。王慧等[5]采用金相檢驗和力學性能等方法，得出了自動扶梯驅動軸疲勞斷裂的主要原因是臺階處倒角設計不合理、機加工不符合要求引起的應力集中。為了預防零件失效，一些學者對軸類結構進行了強度優化設計方法研究，如劉喆等[6]基于四階矩理論的傳動軸結構參數靈敏度分析的數值方法，得到了傳動軸結構參數對其可靠度的影響規律，并在滿足可靠性要求且減輕質量時對傳動軸進行結構優化設計。李秋澤等[7]通過建立驅動系統故障樹和研究萬向軸的運動特性，采用多目標函數優化法確定了萬向軸驅動系統優化方案。普通車輛的驅動軸動力一般為單側輸出，而特種車輛的驅動軸為兩側輸出，因此，載荷的非對稱分布情況對軸的疲勞壽命影響較大。若驅動軸結構設計不合理，會使單側分配的載荷過大，損傷累積過快，從而導致驅動軸的斷裂破壞。

文獻[4]分析了主傳動軸失效的原因，但隨著軸的功率和載荷的增大，仍有一些問題存在。為了控制載荷非對稱分布時驅動軸的低周疲勞失效，本文嘗試在軸的材料和工藝參數已經優化的情況下，從設計方法上對驅動軸進行改進設計，以結構強度和剛度的最優匹配為設計原則，分析軸的兩側剛度比值對載荷分配的影響規律，實現工作過程中驅動軸載荷的合理轉移，均化驅動軸整體的損傷分布，提高驅動軸的使用壽命。

1 驅動軸基本特性描述

1.1 驅動軸工況分析

車輛運行時，傳動系用3個對稱布置的行星齒輪將動力傳遞到驅動軸的中間齒輪上，并由兩側的花鍵輸出。圖1為驅動軸的動力傳遞路線。驅動軸在轉向時由于單側載荷快速增加，右側常出現過載現象。

圖1 驅動軸傳動簡圖Fig.1 Transmission diagram of the driven axle

通過實車測試驅動軸承受的載荷，發現兩側花鍵輸出端在起步換擋工況下的沖擊載荷最大，且兩側花鍵輸出的載荷不相等。圖2為實車測試時兩側花鍵的載荷時間歷程，可以看出，右側花鍵輸出端的最大載荷是9 245 N·m，左側花鍵輸出端的扭矩是4 943 N·m，兩側載荷差值較大。這是由于驅動軸本體為等直徑，致使右側的剛度明顯大于左側的，右側軸的載荷難以向左側軸轉移，造成了兩側花鍵承受的扭矩不同。

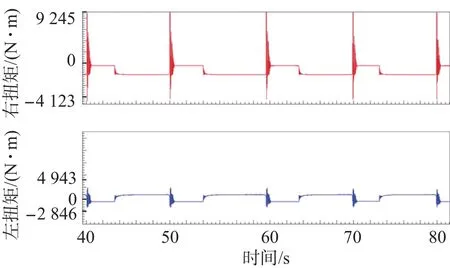
圖2 兩側花鍵輸出端的的載荷時間歷程Fig.2 Load-time history at the output ends of splines on both sides

1.2 驅動軸剛度對載荷分配影響分析

對于驅動軸扭轉剛度而言，其外載荷的表現形式主要是扭矩T，變形是驅動軸的轉角θ，因此，定義扭轉剛度K的計算公式為

驅動軸在純扭轉工況下，扭轉角的計算公式為

式中：l為軸長；G為剪切模量；Ip為極慣性矩，實心軸，；D為軸徑。

代入剛度公式可得

驅動軸中間齒輪相對于兩側花鍵的轉角相等，基于剛度分配法[8-9]的思想，由式（1）可得，驅動軸剛度比與載荷分配的關系式為

式中，下標L，R分別為左側和右側。

結合驅動軸的主要參數（表1），兩側花鍵分配的扭矩隨剛度變化的趨勢如圖3所示。從圖3中可以看出，隨著驅動軸兩側的剛度比KL/KR的增大，右側分配的扭矩逐漸減小，而左側分配的扭矩增大，兩側花鍵分配的扭矩與自身扭轉剛度成正比。驅動軸在實際使用時為純扭轉變形，為了改善斷裂單一出現在右側花鍵齒根的問題，在優化設計時，驅動軸兩側剛度比KL/KR的理想值為1，使得兩側花鍵分配的載荷趨于相等，破壞概率近似相同。

表1 驅動軸參數表Tab.1 Parameters of the driven axle

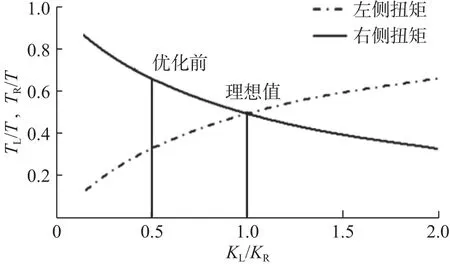
圖3 兩側花鍵的扭矩變化趨勢Fig.3 Torque variation of splines on both sides

驅動軸的動力由兩側輸出，現有設計未考慮驅動軸兩側剛度與強度的匹配，導致驅動軸右側分配的載荷過大，損傷累積較快，從而使驅動軸的右側花鍵處容易發生疲勞斷裂。

2 驅動軸有限元分析

為進一步了解驅動軸的應力分布情況并鎖定強度薄弱區，建立了驅動軸的有限元模型。對驅動軸模型進行幾何清理，并劃分四面體網格。在應力較大或者易產生應力集中的部位應該采用小尺寸的網格，非關鍵區域的網格尺寸可以稍大些[10-11]。根據模型中最小特征至少有3個節點的原則，且軟件在劃分網格時要求最小網格尺寸不小于網格尺寸的5%，本文經過對比后確定網格的尺寸為4 mm，最小網格尺寸為0.2 mm，特征角為10 °。

分別將3個行星輪對中間齒輪的作用力分解為徑向力和切向力。分析得徑向力大小相等，方向均指向中間齒輪的圓心且夾角互為120 °，故徑向力的合力為0，是純扭轉變形。因此，有限元分析的載荷條件：在驅動軸的中間齒輪施加3個切向力，重合度為1.3；邊界約束：對驅動軸兩側漸開線花鍵與配套齒圈采用接觸約束條件，齒圈通過對剛性節點的自由度約束形式（SPC形式）固定約束。最終完成的有限元分析模型如圖4所示。

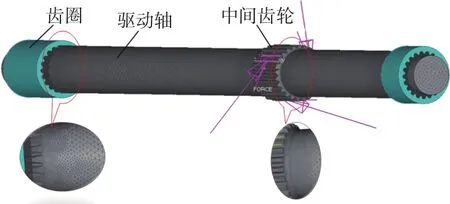
圖4 驅動軸有限元分析模型Fig.4 Finite element analysis model of the driven axle

改變施加在中間齒輪的載荷值，可得驅動軸在不同工況下的應力分布情況，表2（見下頁）為有限元仿真結果，可以得到驅動軸在工況2下兩側花鍵的齒根應力最大，是驅動軸的薄弱區，應力云圖如圖5（見下頁）所示。從圖5中可以得到，驅動軸右側光軸處應力比左側大，右側花鍵的齒根應力明顯大于左側花鍵，幾乎為左側花鍵的2倍，是斷裂破壞的危險區。此外，兩側花鍵分配的載荷分別為5 134 N·m，9 541 N·m，與實車測試結果（圖2中驅動軸兩側花鍵輸出端的最大載荷分別為4 943 N·m和9 245 N·m）差距較小，驗證了有限元模型的準確性。因此，可以判斷驅動軸右側容易發生斷裂破壞的原因是兩側花鍵承受的扭矩不相同，右側花鍵分配的載荷較大，且花鍵齒根處產生應力集中現象，導致損傷累積比左側花鍵快。σL和 σR分別為驅動軸左側和右側的最大應力值。

表2 驅動軸在各工況下的仿真結果Tab.2 Simulation results of the driven axle under different working conditions

圖5 驅動軸在工況2下的應力圖Fig.5 Stress diagram of the driven axle under working condition 2

3 驅動軸分段剛度優化匹配設計

根據驅動軸剛度對載荷分配影響的分析結果和發生早期失效的原因，本文在進行分段剛度優化匹配設計時，同時考慮了驅動軸兩側結構強度和剛度的匹配。在滿足強度和疲勞壽命的條件下，期望軸兩側花鍵所分配的載荷產生的應變值近似相等，或者兩側的損傷累積總和趨于相近，這樣兩側花鍵就會具有近似相同的破壞概率，避免總發生在右側花鍵處的早期疲勞失效現象。為此，驅動軸的壽命預測成為驅動軸分段剛度優化匹配設計的核心。

3.1 驅動軸壽命預測

驅動軸的材料為超高強度結構鋼，抗拉強度為1 655 MPa，疲勞極限為382.5 MPa，彈性模量為200 GPa。基于已有的臺架測試的載荷譜和材料強度參數，建立適用于傳動軸的壽命預測模型，流程如圖6所示。

驅動軸萌生裂紋時，行駛里程均較短，且在工況2下，花鍵根部承受的應力水平大大高于材料的疲勞極限，驅動軸的屈服極限為1 308 MPa，屬于低周疲勞失效。進行低周疲勞壽命分析時，常以應變-壽命曲線（ε-N曲線）為基礎，一般多采用曼森-科芬方程：

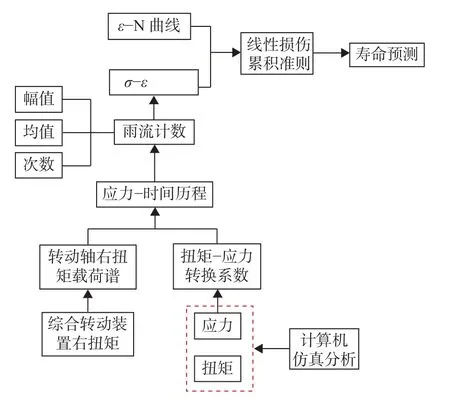
圖6 驅動軸壽命預測流程圖Fig.6 Life prediction process of the driven axle

式中：E為彈性模量，根據選擇的材料，取值為200 GPa；為疲勞強度系數，根據驅動軸材料及工程經驗，取值2 974 MPa；為疲勞塑性系數，取2.075 1；b為疲勞強度指數，取-0.102 6；c為疲勞塑性指數，取-0.781 6。

循環應力-應變曲線擬合公式為

式中：K′為循環強度系數，根據軸的材料，取值為2 468 MPa；n′為循環應變硬化指數，取0.13。

Miner線性損傷準則相對簡單，而且其壽命預測精度可以被工程所接受，因此，本文在預測驅動軸壽命時采用了Miner準則[12-14]。

Miner準則表達式為

式中：D為零件的累積損傷；Ni,f為某一應力水平下的疲勞壽命；ni為某一應力水平下的循環次數。

當損傷D=1時，認為零件發生破壞。在實際計算中，一般可按循環應力-應變曲線將應力幅轉換為應變幅，采用ε-N曲線直接推算出每個應變幅對應的疲勞壽命，最后根據損傷累積理論預測出驅動軸的應變壽命。

根據試驗載荷歷程可知，單次換擋產生的沖擊載荷并不唯一，且疲勞損傷與載荷的均值和幅值密切相關。通過雨流計數法得到一次換擋時的雨流統計圖，如圖7所示。

圖7 均值-幅值雨流矩陣統計Fig.7 Range-mean rain-flow matrix of the driven axle

應力幅值在疲勞極限382.5 MPa以下時，驅動軸接近無限壽命，損傷可以忽略不計[12]。應力幅在疲勞極限以上的雨流循環導致傳動軸的損傷，因此，將疲勞極限以上的應力幅按循環應力-應變曲線轉換為應變幅，根據ε-N曲線得到每個應變水平下對應的疲勞壽命，求出單次換擋的累積損傷為Di，則驅動軸的換擋次數n=1/Di。

3.2 驅動軸優化模型的建立

由式（4）可知， TL/TR達到理想值1可以通過改變DR，DL，lR，lL這4個變量來實現，根據有限元仿真結果，為了改善花鍵齒根應力集中現象，可以采用改變花鍵齒根圓弧r和鍵槽過渡圓弧R的方法。本文考慮到改變lR，lL會影響其他與驅動軸裝配的零部件，且隨著TL/TR靠近理想值，DL會變大，增加了驅動軸的成本，不符合汽車輕量化設計趨勢。因此，為了降低右側花鍵分配的載荷，需將DR，r和R作為優化設計變量。

本文在減小花鍵齒根應力集中的基礎上，采用了改變右側軸徑的方法，建立了以驅動軸疲勞壽命為約束、兩側花鍵的應變值近似相等為目標函數的優化模型。

設計變量：DR，r，R。

約束條件如下：

a. 扭轉強度。

軸右側應力τRmax≤ [τ]

軸左側應力τLmax≤ [τ]

式中： τRmax為 驅動軸右側最大應力； τLmax為驅動軸左側最大應力； [τ ]為應力許用值。

b. 扭轉剛度。

c. 疲勞壽命。

驅動軸的正常使用壽命 N′≥106次，某一檔起步壽命 n′≥4 000次。

邊界約束：20 mm ≤ DR≤4 0 mm；0.6 mm≤r≤1.6 mm；10 mm ≤ R≤50 mm。

根據優化模型求解得到右側軸徑的最優解為36 mm，左側軸徑不變，驅動軸漸開線花鍵齒根圓弧改為1.6 mm，公差等級參考GB/T3478.1-1995，花鍵的其他參數不變，鍵槽過渡圓弧增加到40 mm。

3.3 驅動軸優化后的對比分析

縮小右側軸徑會直接影響到中間齒輪和右側花鍵的幾何特征。為了解決上述問題，分別在中間齒輪、右側花鍵與光軸的交界處預留了過渡區，載荷條件、位移邊界條件和優化前相同，優化后的有限元模型如圖8所示（見下頁）。

表3（見下頁）是驅動軸優化前后的參數對比，可以看出，優化后驅動軸的光軸處的應力都明顯增加，但仍滿足疲勞壽命要求。右側花鍵根部應力明顯下降，與左側齒根部應力的差值減小，表明驅動軸的扭矩分配比有所改善，起步換擋工況下的壽命得到有效提高，且優化后的驅動軸質量減少了9.6%，驅動軸的優化方案可行。

圖8 優化后的有限元模型Fig.8 Finite element analysis model after optimization

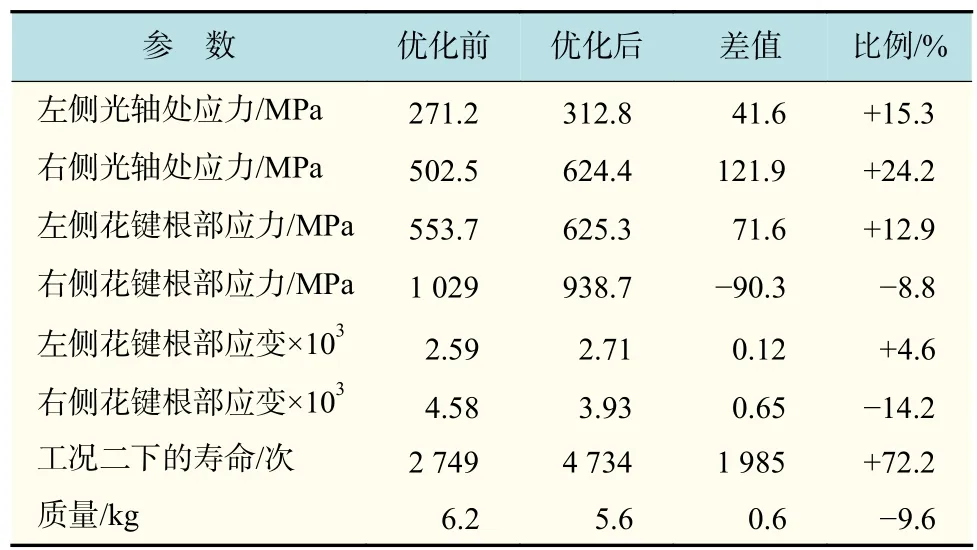
表3 沖擊載荷下驅動軸的參數優化前后對比Tab.3 Comparison of the driven axle parameters under impact load before and after optimization

4 結 論

a. 根據驅動軸非對稱承載的特點和早期失效的原因，得到了軸的剛度比和載荷分配的關系曲線，基于驅動軸兩側剛度匹配的設計原則，建立了以疲勞壽命和強度為約束、兩側花鍵的應變近似相等為目標的驅動軸分段優化設計模型。

b. 通過驅動軸剛度與強度匹配優化的設計方法，從根本上改變軸的強度分布，改善了軸的載荷分配情況，右側花鍵齒根的應力明顯下降，驅動軸的疲勞壽命得到有效提高，且質量減少了9.6%，降低了生產成本。

c. 驅動軸在分段優化設計后，兩側剛度比KL/KR為0.74，與理想值1比較接近。后續可以增加設計變量，進一步使驅動軸的結構優化。