兩個相同部件并聯可修系統解研究
周 莉
( 齊齊哈爾大學 理學院, 黑龍江 齊齊哈爾 161006 )
0 引 言
兩相同部件并聯系統模型是可修系統模型的一種,是一種可靠性數學模型.可修系統模型包含串聯和并聯系統,允許對失效部件進行修理,修理后的部件可繼續執行其使命,使其恢復功能.在實際生產生活中,為了改善系統的可靠性,經常采用維修的手段.由于引入了修理,模型的分析更加復雜.例如Huang等研究了多態連續n中取k可修模型[1-4],補充和深化了可修系統理論.而并聯系統是包含多個部件,且有一個能夠正常工作的完好系統,是具有較強的實用價值的可修系統.王定江[5]討論了兩相同部件并聯可修系統的穩定性并應用強連續算子半群理論證明了系統非負解的唯一存在性;史定華[6]在?p1(x,t)/?t=0條件下用Laplace變換給出了解的Laplace變換公式,即得到了解的存在性.文獻[7]中用C0半群理論研究了這個系統存在唯一非負的時間依賴解.郭衛華[8]用迭代法證明了該系統非負解的存在性和唯一性.本文在兩相同部件并聯系統中用初等階梯函數對其修復率進行逼近,用半離散算法[9-10]將該系統轉化為兩個離散化數學模型,并且運用泛函分析理論證明系統模型動態解的逼近.
1 數學模型
一類兩個相同部件并聯可修系統的模型見圖1.

圖1 兩個相同部件并聯可修系統的模型
該模型可用積分-微分方程組(系統Ⅰ)描述為
(1)
(2)
p1(0,t)=λ(k+1)p0(t)
(3)
p0(0)=1,p1(x,0)=0
(4)
式中:p0(t)表示在時刻t兩個部件完好的概率;p1(x,t)dx表示在時刻t一個部件完好另一個部件故障并且故障的部件在(x,x+dx]內被修好的概率;λ表示部件的平均壽命;μ(x)表示部件的修復率,滿足
0≤μ(x)<∞

k表示正比失效率,k=1時表示并聯,0
2 泛函分析處理
下面在Banach空間中用抽象Cauchy問題的形式來描述這個系統.
設算子
取狀態空間
顯然,X是Banach空間.算子A的定義域為
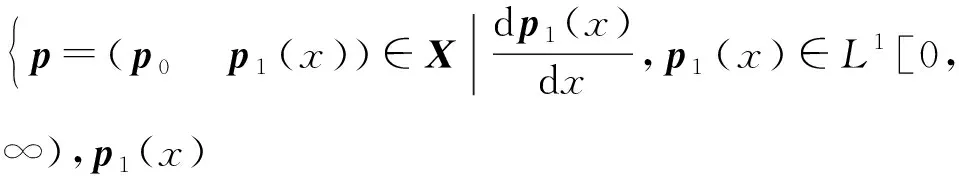
則式(1)~(4)可以描述成Banach空間X中一個抽象的Cauchy問題.

(5)
p(0)=(1 0)T
(6)
3 計算模型半離散化
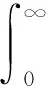
0=a0 令 Δi=[ai-1,ai],x0∈(0,∞) 下面構造階梯函數: 則由假設,對任意的ε>0,存在x0∈[0,∞)使得 |μ(x)-μ*|<ε 與 |μn(x)-μ(x)|<ε 進而原模型經離散后化為式(1)′~(4)′(即原系統的修復率μ(x)置換為μn(x)),則原偏微分方程變為常微分方程系統(1)′~(4)′,如同前面一樣把式(1)′~(4)′用Banach空間中的抽象Cauchy問題來描述: (7) pn(0)=(1 0)T (8) 由線性算子半群對偏微分方程的應用及文獻[11]知:A+B生成一個C0壓縮半群,又因為生成C0半群具有唯一性,所以此壓縮C0半群就是T(t). 首先估計線性算子A+B和(An+Bn)的預解式分別為R(v;A+B)和R(v;An+Bn),然后對系統動態解的逼近問題用Trotter定理加以證明. 考慮方程[vI-(A+B)]p(x)=y(x),即 (9) (10) p1(0)=λ(k+1)p0 (11) 由式(11)可得 (12) 令 將式(12)代入式(9)得 (13) 令 整理得 (v+λ(k+1)(1-ω))p0=y0+φ(y1) (14) 令 |D|=v+λ(k+1)(1-ω)= 所以由文獻[12]得出當v>0時|D|≠0方程(14)的解是唯一的,因此方程組(9)~(11)的解也是唯一的,進而有R(vI-A-B)X,(vI-A-B)是閉算子,且(vI-A-B)-1也存在并且是有界的.而|D|能用ω線性表示,所以當v>0時 (exp(-vx)為減函數)= 即0<|ω|<1,那么|D|也是有界的.所以由式(14)得 將p0代入p1(x)則有 取 因此A+B的預解式為 將(vI-A-B)-1中ω、φ(y1)、W、Q(y1)、|D|含有的μ(x)變為μn(x)得到(vI-An-Bn)-1,相應的ω、φ(y1)、W、Q(y1)、|D|記為ωn、φn(y1)、Wn、Qn(y1)、|Dn|,Λ記為Λn,于是得到 現在來證明系統修復率的逼近,只要證明R(v;An+Bn)y→R(v;A+B)y. 只需證明 且|Dn||D|≠0,|Dn|、|D|有界(n→∞).|D|≠0同理|Dn|≠0,且|Dn|有界,|D|為ω的線性表示,ω中含有μ(x),要證明|Dn|→|D|,只需證明ωn→ω(n→∞). 考慮 則有|ωn|→|ω|(n→∞),即|Dn|→|D|(n→∞). 證明Λn→Λ(n→∞),只需證明相應元素逼近,即 φ(yn)→φ(y1),Wn→W, Q(yn)→Q(y1)(n→∞) μ(ξ)|dξ→0 (n→∞) 0 (n→∞) |μn(x)-μ(x)|· μ(x)|dξdτdx→0 (n→∞) 綜上所述 |Λn|→|Λ| (n→∞) 亦即 即 R(v;An+Bn)y→R(v;A+B)y(n→∞) 這樣就證明了系統動態解的逼近. 為了驗證以上離散后的常微分方程組解的收斂性,用實踐證明理論的正確性.下面利用數值計算方法[13],對上述結果進行數值模擬. (15) (16) p0(0)=1,p1(0)=0 (17) 下面用Matlab數學軟件求常微分方程組的數值解,此時令λ=0.5,μ=0.5,其結果如圖2所示. 對圖2進行分析表明本文建立的離散化模型具有系統動態解.這個結論與理論證明的結論是一致的,進而說明半離散算法對于該可修系統模型是可行的. (a) p0 (b)p1 圖2 系統(Ⅱ)的數值解(μ(x)=μ,為常數) Fig.2 Numerical solution of system (Ⅱ) (μ(x)=μ,is constant) 理論分析表明半離散化逼近方程能夠保持許多原來重要問題的物理意義,所以該逼近方程就可以作為原物理問題的常微分方程模型[14-15].本文利用半離散化方法將兩相同部件并聯可修系統模型轉化為矩陣常微分方程組,證明了該方程組解是收斂的.當假設修復率為常數時對模型解進行數值分析與計算,得到該模型的擬合圖.4 動態解逼近的證明


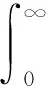
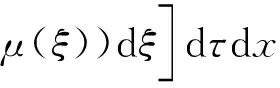



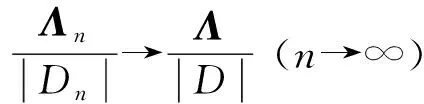






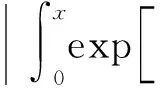






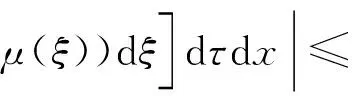




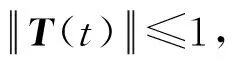
5 數值計算模型
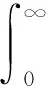
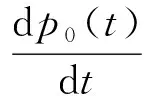


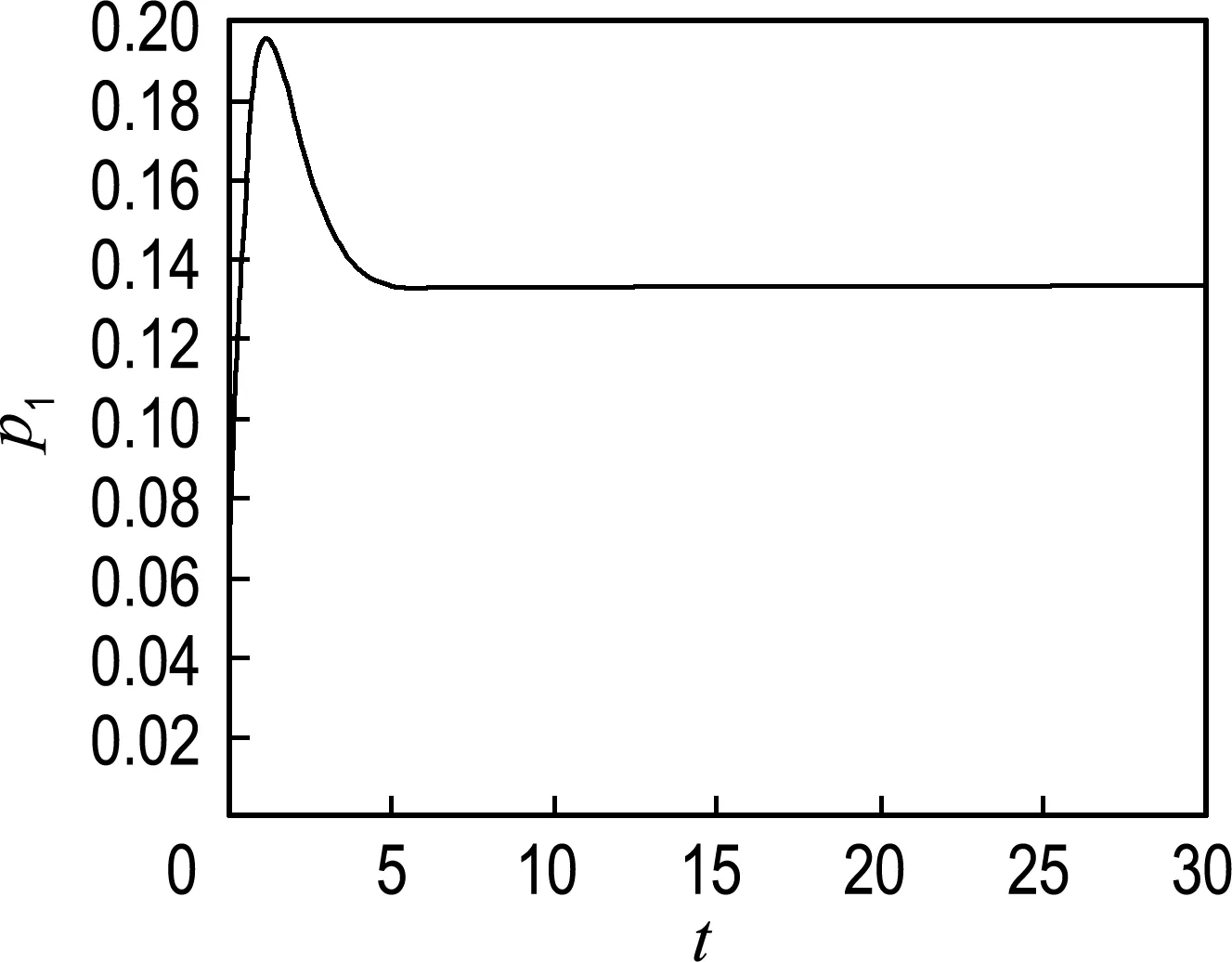
6 結 語

