半變系數伽馬脆弱模型懲罰部分似然估計

張 中 文， 王 曉

( 1.大連理工大學 數學科學學院， 遼寧 大連 116024；2.濱州醫學院 公共衛生與管理學院， 山東 煙臺 264003 )

0 引 言

脆弱模型是比例風險模型的推廣，是考慮隨機效應的生存分析模型．其中，隨機效應(即脆弱)一般用于描述對應于不同分類(例如個體或家庭)的額外風險或者脆弱，其基本思想是不同的個體具有不同的脆弱，相對比較脆弱的個體與其他個體相比更容易發病或死亡．近年來，脆弱模型被廣泛應用于研究對象之間存在不可觀測的組間異質性的非獨立生存時間問題的研究；同時，多種脆弱模型以及擬合這些模型的數值技術被廣泛研究，例如：為了增加模型的靈活程度、擴大模型的應用范圍，Du等提出了一種非參數帶脆弱項的危險率模型[1]；Yu等將多元對數正態脆弱模型推廣到可加半參數情形用以描述協變量對于對數危險率的非線性影響，并提出了一種雙懲罰部分似然法用于模型的估計[2]，該模型在增加了模型適應性的同時，也避免了多元非參數函數的估計問題．

變系數模型是近年來發展起來的具有廣泛應用背景的回歸模型，該模型通過假設回歸系數是其他協變量的未知函數而增加模型的靈活性，因為系數函數通常被假設為某個協變量的一元函數，所以維數災難問題得到了有效避免．如Zhang等研究了半變系數多元脆弱模型的估計問題，用以描述某些協變量對于危險率的影響受其他協變量的影響，并通過數值模擬和實例分析說明了方法的有效性，其中脆弱的分布假定為對數多元正態分布[3]．而在實際的脆弱模型應用過程中，假定脆弱服從伽馬分布更為常見，這是因為伽馬分布的變量為正數，十分適合脆弱分布無符號改變的特性；伽馬分布可以通過Laplace變換獲得導數，從而使得整個模型求導具備相對的簡便性．本文提出一種半變系數伽馬脆弱模型，以進一步豐富脆弱模型的模型結構，用以描述聚集生存數據或者復發型生存數據分析中協變量效應受其他協變量的影響，從而為分析生存時間與協變量更準確、更復雜的關系提供方法學支持．

1 半變系數伽馬脆弱模型

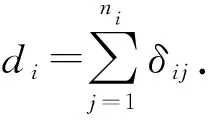
λij(t；xij，uij，wij，νi)=

λ0(t)νiexp(βT(uij)xij+αTwij)

(1)

式中：λ0(t)是基準危險率函數；同時νi(i=1，2，…，s)表示第i個聚類中的脆弱，并且服從單參數伽馬分布，其概率密度函數為

(2)

若令ri=logνi，可稱ri為隨機效應，則半變系數伽馬脆弱模型亦可改寫為

λij(t；xij，uij，wij，ri)=

λ0(t)exp(βT(uij)xij+αTwij+ri)

(3)

假設生存時間Tij與刪失時間Cij關于協變量、隨機效應ri條件獨立，不同個體的生存時間關于隨機效應條件獨立，同時假設隨機效應與刪失時間相互獨立．

2 模型估計方法

2.1 B-樣條

變系數函數向量β(u)可以通過基函數為{B1(u)，B2(u)，…，Bm(u)}的B-樣條進行估計，其中m指樣條基函數的個數，樣條基函數的數量和形狀是由節點個數和位置決定的．本研究在模擬和實例分析過程中選擇m=5．

η1，2…η1，mη2，1η2，2…η2，m…ηp1，1

ηp1，2…ηp1，m)T，并將協變量取值與對應的樣條基函數相乘記為gij=(x1，ijBT(uij)x2，ijBT(uij) …xp1，ijBT(uij))T，則第i個聚類中第j個個體在給定νi以及其他協變量條件下的風險函數可以近似轉化為

λij(t；xij，uij，wij，νi)≈λ0(t)νiexp(ηTgij+αTwij)=

λ0(t)exp(ηTgij+αTwij+ri)

(4)

2.2 懲罰部分似然估計

本文首先在假定θ已知的條件下，采用懲罰部分似然法給出協變量參數的估計，同時隨機效應也假定為回歸參數進行估計[4]．其中，懲罰函數選擇隨機效應的負對數似然函數，由νi的分布可知，ri服從對數伽馬分布，密度函數為

(5)

進一步可以給出半變系數伽馬脆弱模型的懲罰部分似然函數：

lPPL(α，η，r)=lpart-lpen=

αTwij+logνi)-

(6)

類似于線性伽馬脆弱模型[5]，對于固定的θ，可以通過最大化lPPL(α，η，r)獲得α、η、r的估計值．估計過程中，首先假定r為固定效應的回歸系數，然后分別關于α、η、r求lPPL(α，η，r)的得分方程：

(7)

(8)

(9)

其中h=1，2，…，s，且當i=h時，zij，h=1，否則zij，h=0．通過調整各項的排列方式，式(9)可以改寫為

αTwhj+rh)Λ0(yhj)+

(10)

其中

(11)

由牛頓迭代法求解得分方程，可以給出估計α、β、r，進而可以采用Nelson-Aalen法得到基準危險率的估計量λ0．

2.3 隨機效應參數的估計

在假設α、η、r已知的條件下，本文采用近似輪廓似然法估計θ．首先，對于固定的α、η，建立邊際似然函數如下：

αTwij))δijexp(-Λ0(tij)νiexp(ηTgij+

(12)

利用伽馬函數的性質(或者應用Laplace變換)[6]，經過適當計算、整理，均可將邊際似然函數改寫為

(13)

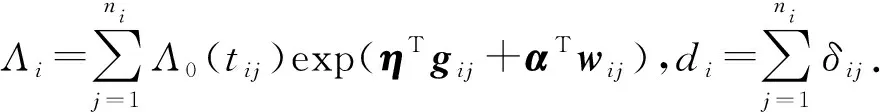
(14)

(15)

利用黃金搜索算法可以得到式(15)的最大值，從而給出隨機效應方差成分的估計θ．

2.4 模型估計流程歸納

現將整個估計流程歸納如下：第1步，運用B-樣條生成新的協變量Gi；第2步，在給定θ初始值的條件下，利用Newton-Raphson算法求解懲罰對數部分似然函數的最大值，從而給出α、θ、r；第3步，對于上一步得到的α、θ、r，通過極大化式(15)得到θ；接下來不斷重復第2步和第3步直到收斂，最后給出α、η、θ最終的估計．

3 數值模擬

本文通過數值模擬的方式對提出的模型及其估計方法進行評價．模擬分為2個部分：(1)所有協變量的系數均是常數系數情形生成的數據集；(2)協變量系數部分為變系數、部分為常數系數情形生成的數據集．考察的模型是半變系數伽馬脆弱模型，其模型結構為

λij(t；xij，uij，wij，νi)=λ0(t)νiexp(β(uij)·

xij+α·wij)；

i=1，2，…，s，

j=1，2，…，ni

模擬中，每個聚類中個體的個數(ni)為5，樣本量分別設定為100、300、500，則對應的聚類個數(s)分別為20、60、100；刪失率分別設定為10%、30%、50%，實際刪失率的誤差控制在0.5%以內；不同情形下，每種模擬的次數設定為500次；刪失時間被設定為服從指數分布，模擬中通過調整指數分布的參數控制刪失率；另設λ0(t)=t，脆弱項νi～Γ(1，1)，即方差(θ)為1的伽馬分布，xij～exp(1)，wij～N(1，1)；常數系數α=1，協變量u在區間(1，3]內按樣本量大小等距取點，在模擬1中β(u)=1，在模擬2中β(u)=cos(2u)+1．

3.1 模擬1

模擬1用于說明本文提出的方法是否適用于所有協變量系數均為常數的情形．不同條件下α、θ的模擬結果見表1．

表1 β(u)=1條件下模型參數的模擬結果

由表1可見，不同條件下α的估計誤差均非常小，即使在刪失率達到50%，而聚類個數僅為20個時，估計偏差也僅為0.034；α標準誤的估計方面，經驗標準誤Semp均略高于估計標準誤Sest，這與相關文獻中的研究結果一致[2-3，7]．不同刪失率條件下，標準誤均隨著樣本量的增大而減小，而相同樣本量條件下，標準誤隨著刪失率的升高而增大．在樣本量較小時，θ的估計誤差相對較大，刪失率的提高會造成θ估計誤差的增大，在樣本量為500時，刪失率的提高對于θ估計的影響較小．

模擬1中，β(u)的估計及其95%置信帶見圖1．篇幅原因，未將樣本量為300或者刪失率為30%的情況顯示，其各自的估計效果介于對應的不同樣本量和刪失率之間．

由圖1可見，不同條件下，β(u)的估計效果均較好，特別是當樣本量為500時，β(u)和β(u)的曲線幾乎是重合的；95%置信帶的曲線形狀與β(u)基本一致，只是邊界有略大的波動，這與文獻結果一致[2-3，8]，置信帶的寬度隨著樣本量的增大而變窄；β(u)的估計偏差同樣受樣本量的影響，樣本量越大，估計偏差越小；在模擬過程中考察的刪失率范圍內，即10%～50%，β(u)的估計偏差無明顯變化，這體現出了本文方法對于不同的刪失率具備一定的穩健性．

(a) 刪失率10%，樣本量100

(b) 刪失率10%，樣本量500

(c) 刪失率50%，樣本量100

(d) 刪失率50%，樣本量500

圖1β(u)=1時不同樣本量和刪失率條件下β(u)的估計

Fig.1 Estimation ofβ(u) in the condition ofβ(u)=1 based on different sample number and censor rate

3.2 模擬2

模擬2用于評價本文提出的方法在半變系數伽馬脆弱模型條件下的擬合效果．不同條件下α、θ的模擬結果見表2．β(u)的估計及其95%置信帶見圖2．

由表2可知，與模擬1的結果類似，不同條件下α的估計誤差仍然都比較小，即使在刪失率達到50%，而聚類個數僅為20個時，估計偏差仍舊不大；α標準誤的估計方面，經驗標準誤也均略高于估計標準誤，這與相關文獻中的研究結果一致[2-3，7]．對于固定的刪失率水平，樣本量的增大可以帶來估計標準誤和經驗標準誤的減小；與此同時，對于固定的樣本量，估計標準誤和經驗標準誤也隨著刪失率的提高而略有增大．在樣本量較小同時刪失率又較高時，θ的估計誤差相對較大，模擬中最大平均誤差達到近0.14；在樣本量較小時，刪失率的提高會造成θ估計誤差較明顯的增大，而在樣本量較大時，刪失率的提高對于θ估計的影響不再顯著．

表2 β(u)=cos(2u)+1條件下模型參數的模擬結果

由圖2可知，對應于不同的樣本量和刪失率，β(u)的平均估計均比較準確，尤其是在樣本量較大(500)時，β(u)和β(u)的圖像幾乎是重合的．與模擬1類似，95%置信帶的曲線形狀與β(u)基本一致，只是在邊界處有相對較大的波動，置信帶的寬度隨著樣本量的增大而變窄；β(u)的偏差同樣受樣本量的影響，樣本量越大，偏差越小；在模擬過程中考察的刪失率范圍內，即10%～50%，β(u) 偏差的變化并不顯著，模擬2和模擬1共同體現出了本文提出方法是比較穩健的．

(a) 刪失率10%，樣本量100

(b) 刪失率10%，樣本量500

(c) 刪失率50%，樣本量100

(d) 刪失率50%，樣本量500

圖2β(u)=cos(2u)+1時不同樣本量和刪失率條件下β(u)的估計

Fig.2 Estimation ofβ(u) in the condition ofβ(u)=cos(2u)+1 based on different sample number and censor rate

4 實例分析

本文通過分析美國北部癌癥治療中心(North Central Cancer Treatment Group，NCCTG)的晚期肺癌數據來評價本文提出的模型與方法的應用效果．調查涉及167名晚期肺癌患者，刪失率為28%，文獻中已經有關于本數據集的一些分析[9-10]，本研究重點考察病人Karnofsky自評分對于危險率的影響受其他因素的影響情況，了解晚期肺癌的預后因素，從而為醫師以及病人制訂更合理的治療方案提供參考．所謂預后是指預測疾病的可能病程和結局，它既包括判斷疾病的特定后果，如康復，某種癥狀、體征和并發癥等其他異常的出現或消失及死亡，也包括提供時間線索，如預測某段時間內發生某種結局的可能性．

納入本研究的評價指標包括機構代碼(I)、生存時間(T)、刪失指標(C)、病人年齡(U)、病人的Karnofsky自評分(X)、性別(W1)、ECOG得分(W2)、卡路里攝入量(W3)．考慮到不同醫療機構的治療水平存在差別，即考慮病人的生存時間在就醫機構方面表現出聚集性，即具有不可觀測的隨機效應，因而將這些變量代入半變系數伽馬脆弱模型，模型結構如下：

λij(t；νi，uij，xij，w1，ij，w2，ij，w3，ij)=

λ0(t)νiexp(β(uij)xij+α1w1，ij+

α2w2，ij+α3w3，ij)

(16)

采用本文提出方法給出各協變量的估計，同時采用bootstrap方法給出95%置信帶的估計，結果顯示，性別以及ECOG得分對于危險率的影響具有統計學意義，男性相比女性危險率更高，ECOG得分越高，危險率也越高，詳見表3．

表3 NCCTG數據回歸參數的估計

圖3顯示，不同年齡段晚期肺癌患者的Karnofsky自評分對對數危險率的影響大小非常數，而是一個非線性函數．

圖3 NCCTG數據分析中變系數函數及其置信帶的估計

Fig.3 Estimation of the varying coefficient function and confidence belt of NCCTG data

5 結 語

經模擬研究和實例分析發現，在樣本量不大的條件下，本文提出的方法即可給出模型線性回歸系數非常準確的估計，刪失率的提高也不會對參數的估計效果造成明顯影響．在樣本量較小同時刪失率又較高的條件下，隨機效應參數的估計誤差較大，這提示在實際的應用過程中本方法有低估隨機效應方差的傾向，當樣本量較大時，隨機效應參數的估計誤差則會明顯減小．本文提出的方法可以給出常數函數非常準確的估計，即適用于所有系數均為線性回歸系數的場合，也即本文的方法包含傳統的線性伽馬脆弱模型作為其特殊形式；同時，本文提出的模型可以給出非線性函數系數非常準確的估計，這也擴展了伽馬脆弱模型的適用范圍和應用領域．

綜上所述，本文提出的方法對傳統的伽馬脆弱模型進行了有效的擴展，方法穩定、計算速度也較快，常數回歸系數以及函數回歸系數的估計對樣本量和刪失率的要求均不高，適宜在實際問題中推廣使用．當然，本研究中也存在一些不足，例如：雖然在模擬研究中給出了變系數函數的置信帶，在實例分析中也應用bootstrap方法給出了變系數函數的置信帶，但未能就函數系數的假設檢驗等問題進行探討，這也有待于接下來更深入的研究．