學會思考掌握方法

邵 娟

學會思考，對同學們來說，是一生中最有價值的本錢.近幾年“數據的集中趨勢和離散程度”在中考中出現的頻率越來越高，相信同學們通過以下的學習，能對初中數學中“數據的集中趨勢和離散程度”的解題策略方法有所了解與掌握.

一、熟知概念，直擊要害

例1 據統計，某住宅樓30戶居民5月份最后一周每天實行垃圾分類的戶數依次是：27，30，29，25，26，28，29，那么這組數據的中位數和眾數分別是（ ）.

A.25和30 B.25和29

C.28和30 D.28和29

【解析】從小到大排列此數據為：25，26，27，28，29，29，30.數據29出現了兩次，所以29為眾數；中間的數是28，所以28是中位數.

故選：D.

例2 一組數據2，1，2，5，3，2的眾數是（ ）.

A.1 B.2 C.3 D.5

【解析】在數據2，1，2，5，3，2中，2出現3次，出現次數最多，所以眾數為2.

故選：B.

【點評】例1、例2屬于基礎題，考查了同學們確定一組數據的中位數和眾數的能力.部分同學往往對這個概念理解不清楚，求解方法不明確.大家注意，找中位數的時候一定要先排好順序，然后再根據奇數和偶數個數來確定中位數.如果數據是奇數個，則正中間的數即為中位數；如果數據是偶數個，則找中間位置兩個數的平均數.注意眾數可以有不止一個.

例3 體育課上，某班兩名同學分別進行了5次短跑訓練，要判斷哪一名同學的成績比較穩定，通常需要比較兩名同學成績的（ ）.

A.平均數 B.方差

C.頻數分布 D.中位數

【解析】方差反映一組數據波動大小，是反映這組數據穩定程度的量.方差越大，表明這組數據偏離平均數的程度越大，即波動越大，反之也成立.故要判斷哪一名同學的成績比較穩定，通常需要比較這兩名同學5次短跑訓練成績的方差.故選：B.

二、熟記公式，直接套用

例4 某排球隊6名場上隊員的身高（單位：cm）是：180，184，188，190，192，194.現用一名身高為186cm的隊員換下場上身高為192cm的隊員，與換人前相比，場上隊員的身高（ ）.

A.平均數變小，方差變小

B.平均數變小，方差變大

C.平均數變大，方差變小

D.平均數變大，方差變大

【解析】方法一（計算）.

原數據的平均數為：

原數據的方差為：

新數據的平均數為：

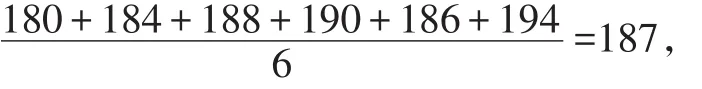
新數據的方差為：

所以平均數變小，方差變小.

方法二（觀察）：從題意可知，192＞186，所以平均數一定變小.同時，這組數據呈上升趨勢，將192換成186，上升趨勢變緩，方差變小.

故選：A.

例5 為了幫助市內一名患“白血病”的中學生，東營市某學校數學社團15名同學積極捐款，捐款情況如下表所示，下列說法正確的是（ ）.

捐款數額10 20 30 50 100人數2 4 5 3 1

A.眾數是100 B.中位數是30

C.極差是20 D.平均數是30

【解析】該組數據中出現次數最多的數是30，故眾數是30，不是100，所以選項A不正確.

該組共有15個數據，其中第八個數據是30，故中位數是30，所以選項B正確.

該組數據的極差是100-10=90，故極差是90，不是20，所以選項C不正確.

該組數據的平均數是：

平均數不是30，所以選項D不正確.

故選：B.

【點評】這兩題屬于中檔題，考查同學們對平均數、極差、方差公式的運用，所以在平常的學習中，同學們一定要熟記本章節的公式，做到“公式不離手，概念不離口”.

三、分析數據，巧用結論

例6 甲、乙、丙、丁4支儀仗隊隊員身高的平均數及方差如下表所示：

乙甲丙丁179 0.6平均數（cm）方差177 0.9 178 1.6 178 1.1

哪支儀仗隊隊員的身高更為整齊？

A.甲 B.乙 C.丙 D.丁

【解析】因為甲、乙、丙、丁4支儀仗隊隊員身高的方差中丁的方差最小，所以丁儀仗隊隊員的身高更為整齊.

故選：D.

例7 如果一組數據6，7，x，9，5的平均數是2x，那么這組數據的方差為（ ）.

A.4 B.3 C.2 D.1

【解析】根據題意，得：

解得：x=3.

則這組數據為6，7，3，9，5，其平均數是6，所以這組數據的方差為：×［（6-6）2+（7-6）2+（3-6）2+（9-6）2+（5-6）2］=4.

故選：A.

【點評】方差是用來衡量一組數據波動大小的量，方差越大，表明這組數據偏離平均數的程度越大，即波動越大，數據越不穩定；反之，方差越小，表明這組數據分布比較集中，各數據偏離平均數的程度越小，即波動越小，數據越穩定.

四、生活數學，數學生活

例8 超市銷售人員在一段時間內銷售了同一品牌不同尺碼的鞋子，它們的銷售量如下表：

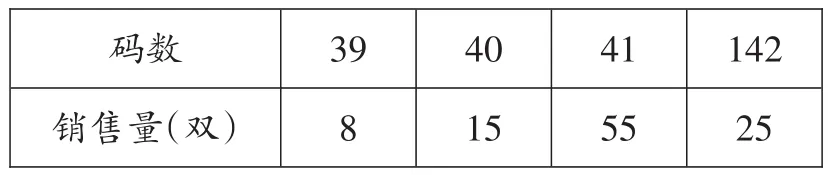
142 25碼數銷售量（雙）39 8 40 15 41 55

建議超市將（ ）的鞋子進貨多一些.

A.39碼 B.40碼 C.41碼 D.42碼

【解析】在4個碼數的銷售量中，41碼的鞋子銷售量最多.

故選：C.

例9 11名同學參加數學競賽初賽，他們的得分互不相同，按從高分到低分進入復賽的原則，取前6名同學參加復賽.現在小明已經知道自己的分數，如果他想知道自己能否進入復賽，那么還需知道所有參賽學生成績的（ ）.

A.平均數 B.中位數

C.眾數 D.方差

【解析】11人成績的中位數是第六名的成績.參賽選手要想知道自己是否能進入前6名，只需要了解自己的成績以及全部成績的中位數，比較即可.由于總共有11個人，且他們的分數互不相同，第六名的成績是中位數，要判斷自己是否進入前6名，故應知道中位數.

故選：B.

【點評】數學來源于生活，而又服務于生活.本題考查了我們實際生活的問題，把實際問題數學化.例8中41碼的鞋子的銷售量比較多，超市肯定將銷售量最多的進貨多一些，考查了同學們的生活經驗.

其實這一章節的內容在中考中對于大多數同學來說是送分題，它主要考查的是基本的概念和公式.希望同學們在學習中理清概念，熟記公式，那么考試時所有的問題都能輕松應對.

小試牛刀

1.某小區20戶家庭的日用電量（單位：千瓦時）統計如下：

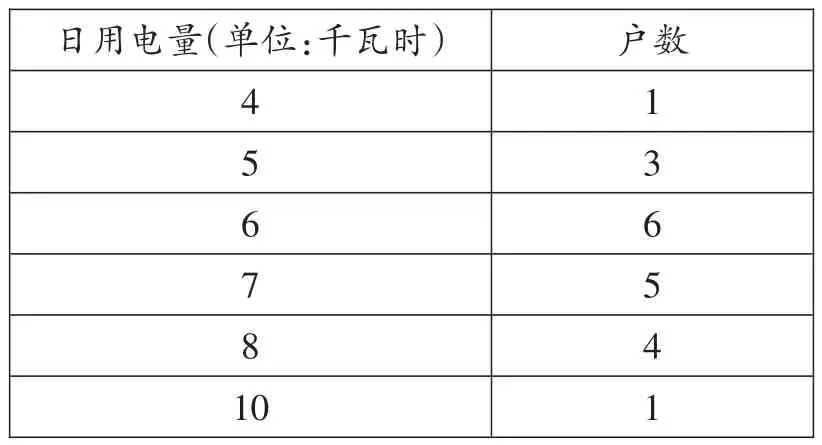
日用電量（單位：千瓦時）戶數4 5 6 7 8 1 0 1 3 6 5 4 1

這20戶家庭日用電量的眾數、中位數分別是（ ）.

A.6，6.5 B.6，7

C.6，7.5 D.7，7.5

2.九年級一班和二班每班選8名同學進行投籃比賽，每名同學投籃10次，對每名同學投中的次數進行統計.甲說：“一班同學投中次數為6個的最多.”乙說：“二班同學投中次數最多的與最少的相差6個.”上面兩名同學的議論能反映出的統計量是（ ）.

A.平均數和眾數 B.眾數和極差

C.眾數和方差 D.中位數和極差

3.甲、乙、丙3人進行飛鏢比賽，已知他們每人投5次的成績如圖，那么3人中成績最穩定的是 .

4.學校商店在一段時間內銷售了4種飲料共100瓶，各種飲料的銷售量如下表：

品牌銷售量（瓶）甲乙丙丁12 32 13 43

建議學校商店將（ ）品牌的飲料進貨多一些.

A.甲 B.乙 C.丙 D.丁

掃二維碼關注公眾號，輸入“2018年11月數學”查答案。