一道例題引發的思考
王玉珍

有位同學在學習蘇科版《數學》九年級上冊第四章“等可能條件下的概率”的一道例題后,與老師交流了自己的思考,具體內容如下:
一、例題再現
一個不透明的袋子中裝有1個白球和2個紅球,這些球除顏色外都相同,攪勻后從袋中任意摸出1個球,記錄顏色后放回、搖勻,再從中任意摸出1個球.求兩次摸到紅球的概率.
【解析】從題目中的“不透明”發現這是一個隨機事件,把兩個紅球編號,再“搖勻”,說明摸到每一個球的機會均等,所以這是一個等可能事件.借助樹狀圖或表格列出所有可能的結果,再代入等可能條件下的概率公式即可求出.
把兩個紅球編號為紅球1、紅球2,用表格列出所有可能的結果:

第二次摸球結果白紅1紅2第一次摸球白紅1紅2(白,白)(紅1,白)(紅2,白)(白,紅1)(紅1,紅1)(紅2,紅1)(白,紅2)(紅1,紅2)(紅2,紅2)
由表格可知,共有9種可能出現的結果,并且它們是等可能的.將“兩次都摸到紅球”記為事件B,它的發生有4種可能,所以事件B發生的概率為:P(B)=.即兩次都摸到紅球的概率是.
【點評】本題屬于摸兩次球的情況,可以用樹狀圖或表格列出所有可能的結果.
二、拓展
思考1:如果把例題中的“放回”改為“不放回”,應該怎么做呢?
【解析】本題是一個求等可能條件下的概率問題,“不放回”就是摸到一個球以后,下次再摸就不會摸到同一個球.
把兩個紅球編號為紅球1、紅球2,用表格列出所有可能結果:

第二次摸球結果白紅1紅2第一次摸球白(白,紅1)紅1紅2(紅1,白)(紅2,白)(白,紅2)(紅1,紅2)(紅2,紅1)
由表格可知,共有6種可能的結果,并且它們是等可能的.將“兩次都摸到紅球”記為事件B,它的發生有2種可能,所以事件B發生的概率P(B)==.即兩次都摸到紅球的概率是.
【點評】“不放回”表格內的數據要少一些,不出現的情況用斜線劃掉,所以遇到概率問題時我們要看清題目中的關鍵詞.
思考2:如果把例題中兩個紅球拿掉1個,又按照之前的方法再摸一次,求3次都摸到紅球的概率.應該怎么做呢?
【解析】本題是一個求等可能條件下的概率問題.表格只適用于兩次摸球的情況,3次就不夠用了,所以本題只能用樹狀圖列出所有可能的結果.
用樹狀圖列出所有可能的結果:
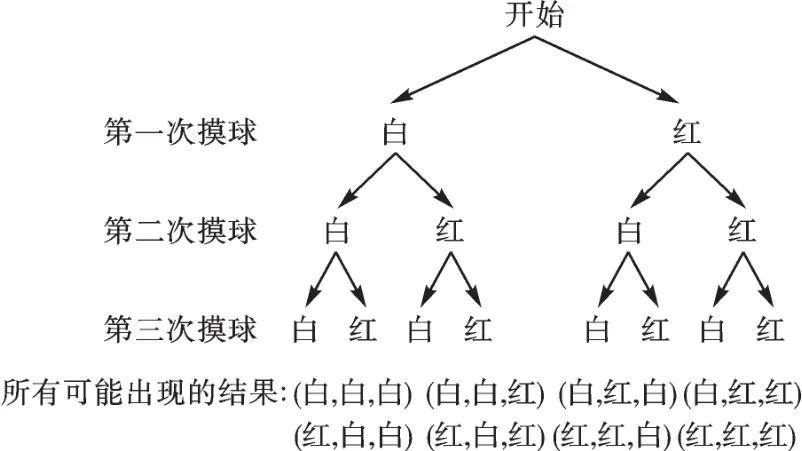
由上圖可知,共有8種可能的結果,并且它們是等可能的.將“3次都摸到紅球”記為事件B,它的發生有1種可能,所以事件B發生的概率:P(B)=.即3次都摸到紅球的概率是.
【點評】課本例題出現過橫著畫的樹狀圖,如果摸3次的話,縱向占用的空間比較大.
思考3:如果把例題中“放回”改為“不放回”,又按照之前的方法再摸一次,求“前兩次摸到紅球,最后一次摸到白球”的概率.這又應該怎么做呢?
【解析】解題思路與思考2類似.再抓住題目中的關鍵詞“不放回”即可.
把2個紅球編號為紅球1、紅球2,用樹狀圖列出所有可能的結果:

由上圖可知,共有6種可能的結果,并且它們是等可能的.將“前兩次都摸到紅球,最后一次摸到白球”記為事件B,它的發生有2種可能,所以事件B發生的概率:P(B)==.即前兩次都摸到紅球,最后一次摸到白球的概率是.
【點評】沿用思考2中的畫圖方法,同學們可將此處的樹狀圖橫向繪制,感受一下解題方法的多樣性.
三、小結
遇到問題,我們應該仔細、認真讀題,抓住題目中的關鍵詞,搞清題目的意思,再“對癥下藥”.比如兩次摸球,既可以用表格,也可以用樹狀圖列出所有可能的結果,用哪一種更好呢?筆者認為,球的總數在4個以內,同學們可根據自己的喜好隨便選,但總數等于或超過4個的話,用表格可能更好一些.另外,列表格時題目中出現“不放回”,需把不出現的情況用斜線劃掉.再比如3次摸球,表格就滿足不了,只能用樹狀圖列出所有可能的結果了,橫著畫還是豎著畫,就根據個人喜好了.

