改進集合平方根濾波的目標跟蹤算法?

張家葉子 呂 游 王華松

（1.92941部隊 葫蘆島 125000）（2.91899部隊 葫蘆島 125001）

1 引言

在非線性的系統模型中濾波算法包括擴展卡爾曼濾波（EKF）、集合卡爾曼濾波（EnKF）、集合平方根濾波（EnSRF）和粒子濾波等。其中，集合平方根濾波［1］采用了相關統計信息的低秩表示，計算簡單。粒子濾波的不限制系統和測量模型或噪聲的分布情況，自舉濾波器和輔助自舉粒子濾波器［2～6］則基本解決了粒子濾波中粒子的多樣性問題。

2 系統模型

在本文中，我們采用了一個未知轉彎率的坐標轉彎模型［7］，目標狀態向量 xk由 [ ]xk,x˙k,yk,y˙k表示，xk，yk表示代表目標的坐標，x˙k，y˙k代表目標在x和y方向的速度。轉彎率為狀態向量中的未知參數，需要在每一個時刻進行估計。系統模型為

T為采樣間隔。Ω代表轉彎率，是目標速度的非線性函數，模型是非線性的。以轉彎率為擴展狀態的狀態向量可表示為

系統轉移函數表示為

假設測量設備定位在原點使觀測值由方位角測量模型化：

多個觀測值來自不同的目標和雜波，每一個獲得的測量值或者關聯到一個目標，或者被視作無效測量值而丟棄。本文改進了聯合概率數據關聯（JPDA）技術［8～9］。

3 濾波技術

在目標跟蹤中，通過隨機濾波算法估計單目標的狀態。自舉濾波器一般由貝葉斯遞歸濾波實現。自舉濾波器的主要缺點是，當所估計的PDF分布不均時，需要更大的粒子數。輔助自舉濾波器使用輔助變量來幫助選擇最具代表性的粒子，在低過程噪聲的情況下性能較自舉濾波器有很大提高。

3.1 集合平方根濾波器EnSRF

集合平方根濾波器EnSRF［10］是從集合卡爾曼濾波器（EnKF）導出的。它的主要優點是對涉及的統計信息的低秩表示。平方根濾波器通常使用一些非唯一變換將預測相位參數變換到分析相位參數。在EnSRF中，m成員集合稱為{xi,(i=1,…,m)}，用于表示n維狀態空間。在濾波器中使用的集合均值由下式給出：

集合擾動矩陣實際上是集合協方差矩陣的矩陣平方根。EnSRF具有處理傳達集合統計信息的低維擾動矩陣的優點。

EnSRF涉及預測階段和分析階段，，預測步驟與在粒子濾波中執行的預測相同。預測觀測集合定義為

分析參數為

如果預測和觀測模型是線性的，當m→∞時上面給出的更新方程收斂到傳統的卡爾曼濾波。

3.2 帶粒子更新的集合平方根濾波器

帶粒子更新的集合平方根濾波器［11］是EnSRF的變體，集合通過EnSRF的分析階段傳播。它的優點是在每個時間步驟的集合分析中都不依賴于高斯分布假設。分析集合可以從預測集合獲得：

i代表集合的索引。在EnSRF中，它是預測集合的平均值，有助于分析整體平均值，但在本算法中，它的每個元素都用在分析中起到作用。

3.3 基于樣本的聯合概率數據關聯

本文中使用基于樣本的聯合概率數據關聯［12］來消除測量源的不確定性，基于聯合概率的數據關聯被集成到用于狀態估計的粒子濾波器中。這里，將各樣品用元組(n,n)代表，是重要性因子或與狀態相關的權重。在基于聯合概率的數據關聯中估計權重 βji，表示測量j屬于目標i的概率。在基于樣本的聯合概率數據關聯中，該因子由下式給出：

θ表示聯合關聯事件，唯一地確定每個觀測值到其相應目標之間的關聯。mk表示已經驗證的測量數量，α是歸一化因子，γ表示觀察到的測量是虛假值的概率。一旦分配概率可用，則樣本的權重被計算為

3.4 基于樣本的聯合概率數據關聯和帶粒子更新的集合平方根濾波器

所獲得的分配概率βji可以并入帶粒子更新的集合平方根濾波器框架中來保管多個目標觀測值。采用基于樣本的聯合概率數據關聯分析粒子：

這種權重改變將強化更新中最恰當測量的作用，同時降低所有其他測量的影響。

4 仿真實驗

本文實驗的目標跟蹤工作是在對三個濾波器進行模擬和比較，主要是自舉濾波器，輔助自舉濾波器和帶粒子更新的集合平方根濾波器。

軌道遵循協調轉彎模型，對于粒度為50模擬繪制30個時間步長的結果。軌道的初始位置坐標取為（-5，-4），相應的初始轉彎率別為0.7。

繪制100蒙特卡洛運行的均方根誤差（RMSE）和樣本方差，并用于比較三個濾波器的性能。圖1和圖2示出了自舉濾波器，輔助自舉濾波器和本文的方法的跟蹤性能。從這些曲線圖可以看出，與自舉濾波器和輔助自舉濾波器相比，本文的方法顯示出優越的跟蹤性能。軌跡的RMSE圖如圖3所示。與其他兩個濾波器相比，本文的方法具有最低的RMSE值。輔助自舉過濾器的RMSE性能高于自舉過濾器。

從樣本方差圖看出，本文方法在所有給定的圖示中清楚地給出最低RMSE值，并給出一致的跟蹤性能。雖然輔助自舉濾波器的性能比自舉濾波器更好，但是比本文方法和自舉濾波器速度慢。表1中比較了三種濾波器的執行時間。自舉濾波比本文的方法快，但其跟蹤性能差。因此，本文的方法可以說是對當前問題的一個更快、更準確的解決方案。

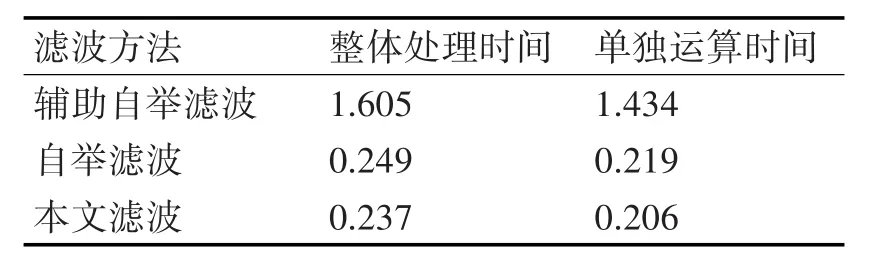
表1 執行時間

5 結語

本文通過將基于樣本的聯合概率數據關聯納入狀態估計算法來實現數據關聯。將提出的濾波器的結果與自舉濾波和輔助自舉濾波算法進行比較，實驗結果表明，與自舉濾波和輔助自舉濾波相比，所提出的融合基于樣本的聯合概率數據關聯和集合平方根的濾波檢測結果更加準確，數據關聯更加有效，運算簡單，速度更快，提供相同的跟蹤性能所需的總體粒度比由自舉濾波和輔助自舉濾波小得多。