方差分析在雷達精度試驗數據處理中的應用?
馬 強
(92941部隊 葫蘆島 125001)
1 引言
在雷達試驗中,精度是試驗考核的重要項目之一。雷達精度試驗的方法目前主要有基于GPS的校飛方式[1]、跟蹤衛星方式[2]、基于精密設備測量的方式[3]和基于ADS-B數據的標校方式[4~5]等四種方法。雷達精度試驗主要考核距離、方位、俯仰、速度等項目指標。這些指標結果對不同的雷達會產生不同的影響,對于引導雷達,不能夠為其他設備提供準確的目標引導信息,而對于火控雷達,則將影響武控系統是否能夠有效攻擊目標[6]。影響雷達精度的因素有很多,如與雷達本身、目標特性和空間傳輸環境等因素[7]。為了判斷這些因素對雷達精度產生的影響,可以合理地設置不同影響因素搭配的試驗,利用方差分析技術對這些因素進行分析。
方差分析又叫變量分析,是英國著名統計學家費希爾于20世紀初提出的,用于兩個及兩個以上樣本均值差別的顯著性檢驗[8]。在實踐過程中,影響系統性能的因素往往很多,利用方差分析可以從這些因素中找出哪種是主要因素,哪種是次要因素,進而對這些因素進行控制,以提升系統的性能。
本文主要運用方差分析方法,以目標海拔高度為例,探究這一因素對雷達距離精度是否產生顯著性的影響。
2 方差分析原理介紹
方差分析的基本思想是:通過分析研究不同變量的變異對總變異的貢獻大小,確定變量對研究結果影響力的大小。通過方差分析,分析不同的水平變量是否對結果產生了影響。如果產生了顯著性的影響,那么它和隨機變量共同作用,必然會使結果有顯著的變化;如果沒有顯著影響,那么結果的變化主要由隨機變量起作用,和分析的變量關系不大。
2.1 方差分析的三個假定
在應用方差分析時,要求對研究的數據滿足如下三個假定:
1)被檢驗的各個總體都服從正態分布;
2)各個總體的方差相等;
3)從每一總體中抽取的樣本是相互獨立的。
這三個假定,都可以用統計方法進行驗證。對第一個假定可以用正態性檢驗方法如夏皮洛—威爾克檢驗[9]方法進行判斷,當試驗數據不服從正態分布時,可以采用數據轉換的方法使之變為服從于正態分布的數據,常用的數據轉換方法有平方根轉換、反正弦轉換、對數轉換和倒數轉換等方法。對于第二個假定,可以利用方差齊性檢驗的方法進行驗證,方差齊性檢驗的方法主要有Hartley檢驗、Bartlett檢驗和修正的Bartlett檢驗等方法[10],當試驗數據不滿足方差齊性條件時,可以將異常的觀測值剔除,但剔除數據時要小心,以免丟失重要信息,也可以將試驗資料分成幾部分,使每部分具有相同的誤差方差。對于第三個假定,可以使試驗按隨機次序進行,以保證各次試驗獨立。
方差分析方法是需要在上述三個假定都滿足的情況下才能進行。
2.2 單因素方差分析
設單因素A有a個水平A1,A2,…,Aa,在水平Ai(i=1,2,…,a)下,進行ni次獨立試驗,樣本取值為 xi1,xi2,…,xini,它們來自具有相同方差σ2,均值分別為 μi的正態總體 N(μi,σ2)。其中 μi,σ2均為未知,并且不同水平Ai下的樣本之間相互獨立。
單因素的數據結構模型如下:
在上式中,εij為試驗隨機誤差。方差分析的任務就是對上述模型中a個總體N(μi,σ2)中各 μi的相等性進行假設檢驗,既有
原假設 H0:μ1=μ2=…=μa
備擇假設 H1:μi≠μj,至少有一對這樣的 i,j。
單因素方差分析的步驟如下:
在上式中,fT為ST的自由度。可以將ST分解:(1)單因素A不同水平下的樣本均值與總平均值間的變異,用SA表示,叫做因素A的效應和;(2)在Ai水平下的樣本均值與樣本值xij之間的變異,用SE表示,它是由隨機誤差引起的,叫做誤差平方和。SA和SE為
在上面兩式中,fA、fE分別為SA和SE的自由度。則有
2)計算均方和及其F值。因素A和誤差E的均方和為
3)選擇合適的顯著性水平α,對原假設進行檢驗 。 若 F>Fα(fA,fE),則 拒 絕 H0;反 之 ,若F<Fα(fA,fE)則接受原假設。
2.3 參數估計
當檢驗結果為顯著時,可以使用點估計和區間估計的方法對總均值、各水平均值和誤差方差進行估計。這些參數的最大似然估計為
2.4 多重比較
如果方差分析的結果因子A顯著,可以認為因子A的各水平效應不完全相同,此時,我們還需要進一步確認哪些水平均值間是有差異的,哪些水平間無顯著性差異。
在r(r>2)個水平均值中同時比較任意兩個水平均值間有無明顯差異的問題稱為多重比較[11~12]。
常用的多重比較方法有最小顯著極差法[11]、最小顯著差數法(LSD)[11]、Tukey檢驗法[12]等方法。
3 單因素方差分析對雷達距離精度試驗的結果分析
在某型雷達精度試驗中,選用海拔高度作為試驗變量,其他影響因素盡量保持一致。該變量共有a=3個試驗水平,它們分別為10000m、100m和35m,雷達一次差數據相應地為x1,x2,x3,樣本量均為n=44。現在使用方差分析技術來判斷海拔高度這一變量是否對雷達跟蹤精度產生顯著性影響。三個水平下的雷達跟蹤一次差圖如圖1所示。
3.1 試驗數據的三個假定性判斷
判斷三個水平下的試驗數據是否滿足方差分析所要求的三個假定。
1)正態性檢驗
本文在這里采用夏皮洛-威爾克檢驗方法,該方法的檢驗統計量為
其中系數a1,…,an為在樣本容量n時有特定的值,需要查閱相關表格,x(i)為待檢驗數據x的次序統計量。相應的拒絕域為
經過計算在三個試驗水平下的W值分別如下:
三個W值大于在顯著性水平α=0.05下的W0.05=0.944(n=44),可以認為在三種不同海拔高度下的雷達一次差數據服從與正態分布。
2)方差齊性檢驗
方差齊性檢驗方法,本文在這里采用Bartlett檢驗方法。該方法的檢驗統計量為
其中 fi、分別為r=i水平下的自由度和樣本方差,其中C為
經過計算三種不同海拔高度下的樣本的統計量B為2.9715,在α=0.05的顯著性水平條件下,(3-1)=5.9915。說明三個水平下的樣本滿足-0.05方差齊性要求。
3)獨立性檢驗
由于三個不同海拔高度下的雷達精度試驗均是獨立進行的,因此三個樣本的數據可以保證為是互相獨立的。
3.2 試驗數據的方差分析
使用方差分析技術對試驗數據進行分析,分析的結果如表1所示。

表1 單因素方差分析結果表
在 α=0.01的 顯 著 性 條 件 下 ,F0.01(2,129)=4.77。F=357.20大于F0.01(2,129),故拒絕原假設H0,接受H1。該結果說明目標海拔高度對雷達精度產生了顯著性影響,需要進一步研究分析。
3.3 雷達精度參數估計
使用點估計和區間估計,對雷達精度試驗的參數進行估計。令α=0.05,誤差方差的無偏估計為σ?2=MSE=0.28,各水平均值的1-α置信區間為
3.4 多重比較
本文在這里采用LSD法進行多重比較。LSD法被稱為最小顯著性差數法,是指兩個處理的平均數差數達到顯著的最小尺度,其計算公式為
當 ||μi-μj>LSDα,則認為 μi與 μj間存在顯著性差異,否則,無顯著性差異。
LSD0.05=0.2212,LSD0.01=0.2923。使用梯形表將多重比較結果表示如表2。
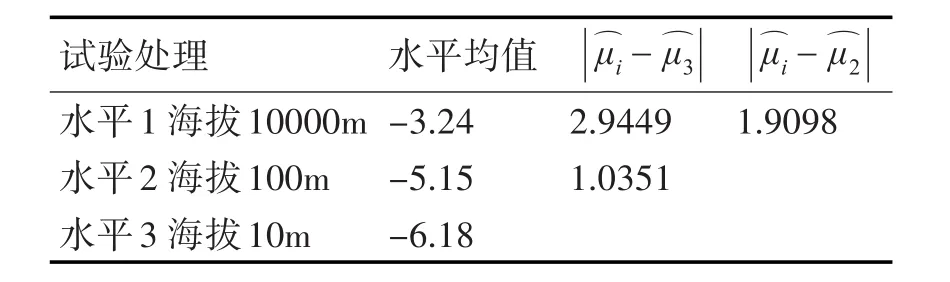
表2 多重比較結果表
4 結語
影響雷達距離精度的因素有很多,本文在這里主要針對目標海拔高度這一因素進行了分析。首先對試驗數據是否滿足方差分析的三個假定進行了判斷;其次利用方差分析判斷這一因素對距離精度是否產生顯著性影響,在結果顯著的基礎上,對試驗參數進行了點估計和區間估計;最后進行了多重比較分析,進一步地查明哪些試驗水平均值間存在顯著性的差異。
當然,方差分析方法可以用于其他多種因素對雷達精度的影響分析。分析得到的結果,對于研制方,可以修正已有設計的不足,改進設計和使用材料,對于使用方,明確知道性能不足的范圍,在使用時進行規避,以發揮雷達的最大效能。

