不等肢L形鋼管混凝土壓彎構件承載性能分析

趙滇生,葉國強

(浙江工業大學建筑工程學院,浙江 杭州 310014)

異形鋼管混凝土構件由外部鋼管和內部混凝土共同受力,兩者優勢互補,相輔相成。國內關于這方面的研究主要集中在以下幾個方面：1)軸壓短柱、偏壓短柱的靜力性能研究[1]；2)軸壓、偏壓構件的抗震性能研究[2]；3)不同加勁措施對異形鋼管混凝土柱的承載能力和延性的影響研究[3]。本文采用纖維模型程序分析了不同參數對不等肢L形鋼管混凝土柱雙向壓彎承載性能的影響,參數包括鋼材的屈服強度、混凝土的抗壓強度、荷載角和軸壓比等。

1 纖維模型法

本文采用的纖維模型程序的基本假定、材料的本構關系以及建立過程見文獻[4]。構件的加載方式、單元劃分、截面尺寸見圖1。其中N為軸力,e為偏心距,l為構件長度,Δ為跨中側移,d為肢高,b為肢寬,h為肢厚,θ為加載角。

圖1 截面單元劃分和構件變形

程序的具體計算步驟如下：

1)輸入構件的具體參數,包括構件截面尺寸、截面劃分單元數目、沿x方向的初始位移Δx,假定形心處的初始應變,以及跨中截面初始彎曲的側向撓度δ值。

2)由x方向的位移Δx,代入公式φx=π2Δx/l2得到x方向的曲率。假定y方向的曲率φy,其初始值可設為φy=φx/tanθ。

3)由已給定的形心處初始應變ε0,以及已經求出的x方向y方向曲率φx、φy,代入以下公式求出截面第i單元的形心處應變：

εi=ε0+φxyi+φyxi

(1)

式(1)中：xi、yi分別為單元形心處的坐標值。

4)將各單元形心處的應變值代入相應材料的本構關系函數式中求出各單元的形心處的應力值σi。各個單元的面積為Ai。則跨中截面的內力Nj、彎矩Mjx、Mjy,可通過累加得到如式(2)～(4)所示。

(2)

(3)

(4)

式(2)中：n為劃分單元的總數。

5)由Nx=Mjx/(ex+Δx+δ)求Nx,判斷Nx與Nj是否相等,若相等則進行下一步,若不相等則調整ε0回到步驟4)。

6)由Ny=Mjy/(ey+Δy+δ)求Ny,判斷Ny與Nj是否相等,若相等則進行下一步,若不相等則調整φy回到步驟3)。

7)給跨中截面強軸方向增加一個撓度增量δΔx,即Δx=Δx+δΔx。重復2)～7)步驟,可得到構件跨中截面的荷載-位移全過程曲線,即N-Um曲線。

2 自編程序與有限元的計算結果比較

分別采用有限元軟件ABAQUS和纖維模型程序對不等肢L形鋼管混凝土雙向偏壓構件進行分析,該不等肢L形鋼管混凝土偏壓構件的詳細參數見表1,兩者計算結果對比見圖2。

表1 LR4試件參數

注：t為鋼管厚度,fy為鋼管屈服強度,fc為核心混凝土軸心抗壓強度設計值。

圖2 程序計算結果與有限元計算結果對比

從圖2中可以看出,ABAQUS和自編程序計算的構件極限承載力十分接近。在彈性階段有限元軟件結果和自編程序計算結果吻合很好,但在彈塑性階段自編程序繪制的曲線過于剛硬,在極限承載力對應的跨中截面撓度上,自編程序的計算結果偏小。在下降段ABAQUS計算得到的曲線下降較為緩慢,自編程序計算得到的曲線下降陡峭。這可能是由于在ABAQUS中為三維實體模型,在加載過程中由于套箍作用的影響,混凝土的承載力下降較單軸受壓緩慢,而自編程序采用的是混凝土的單軸壓本構關系,故下降較為陡峭。但總體來看自編程序的計算結果還是較為準確的。

3 參數分析

構件的N-Mx-My構成空間曲面[5],本節取表2的試件采用自編的N-M程序和Mx-My程序分析不等肢L形鋼管混凝土偏壓構件的相關參數的影響。

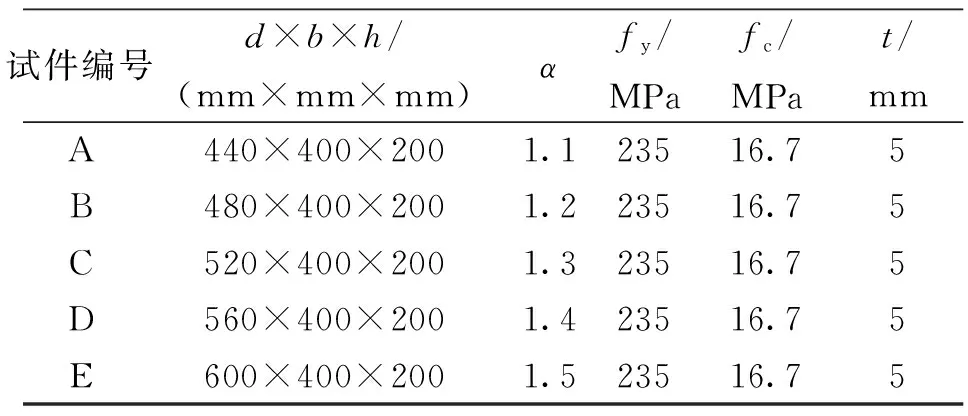
表2 L形截面異形柱參數表

注：表中α為肢高與肢寬之比即α=d/b。

3.1 荷載角

荷載角的取值范圍為0°到180°間距為15°,如圖3所示不等肢L形偏壓柱在不同荷載角下加載時,其N-M相關曲線兼具有鋼柱和鋼筋混凝土柱的特點。在不同荷載角下各試件的N-M相關曲線有很多共同點,總體來說在小荷載角下加載,各試件的N-M相關曲線較為集中。在75°～120°之間加載時,構件的抗彎承載力逐步提高,曲線逐漸趨于平緩,拐點不明顯。在120°方向時構件的抗彎承載力最高,與之對應的在30°方向下加載構架的抗彎承載力最小,原因是120°方向最接近繞截面強軸受彎,而30°方向最接近繞截面弱軸受彎,故在上述兩者方向上加載時抗彎承載力分別為最強和最弱。

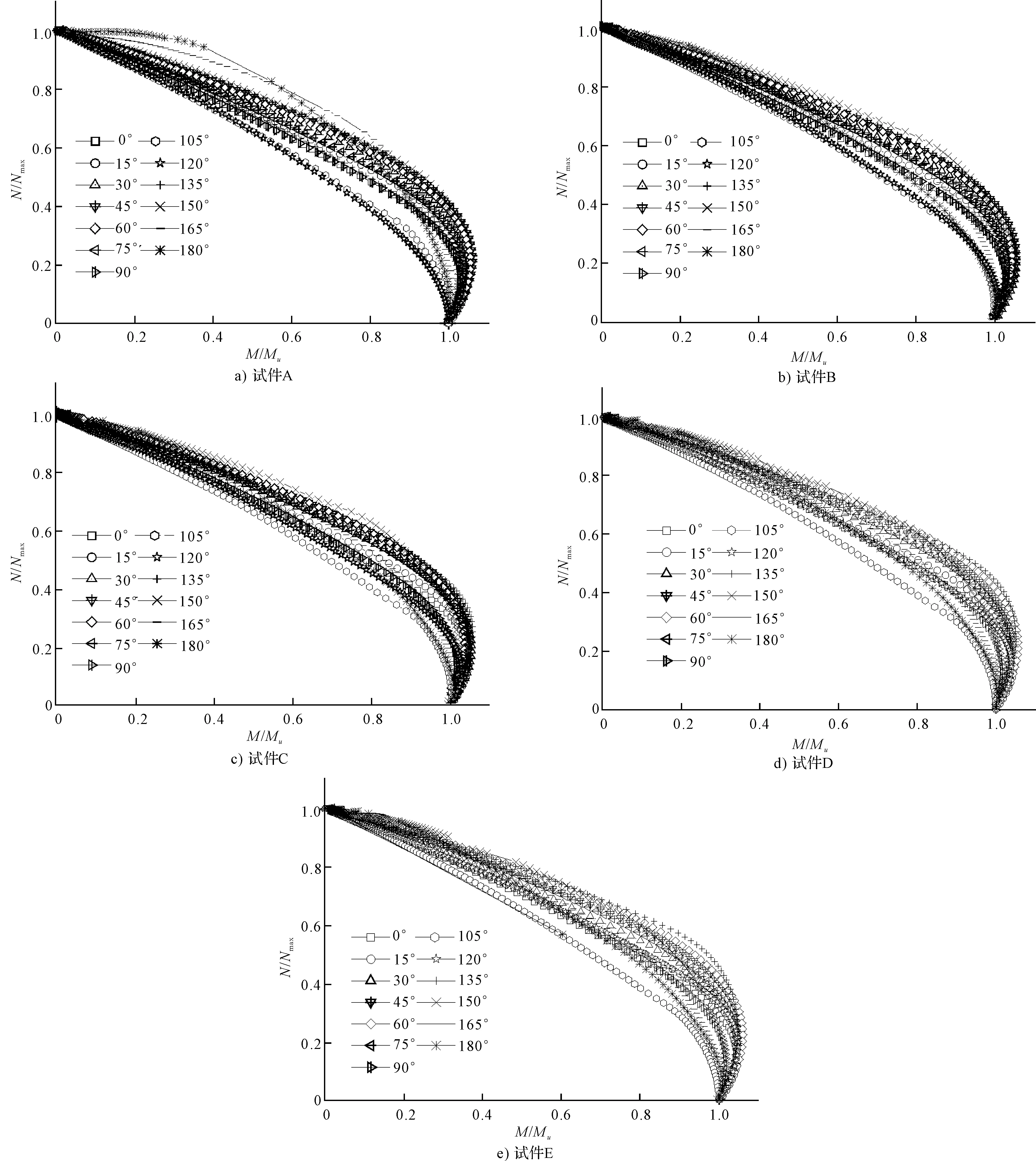
圖3 各試件不同荷載角下的N-M相關曲線

3.2 軸壓比

在不同軸壓比時5個試件的Mx-My的相關曲線見圖4。從圖4可以看出不等肢L形鋼管混凝土柱的Mx-My相關曲線不具有對稱性,在軸壓比較小時(n≤0.3時),Mx-My相關曲線呈橢圓形,當n>0.3時,Mx-My相關曲線呈三角形。在軸壓力系數較小時,曲線的包絡面積較大,隨著軸壓比的增加,曲線包絡面積也隨之減小。在軸壓比在0.3及以下時,曲線的包絡面積變化不大,但當軸壓比大于0.3時,曲線的包絡面積迅速減小。這說明在軸壓比較小時,N-Mx-My曲面坡度較小,即曲面較平緩,抗彎承載力變化不大,較為穩定。但在軸壓比較大時,N-Mx-My曲面坡度較大,即曲面較陡峭,抗彎承載力變化較大,說明高軸壓比時構件抗彎承載力會明顯下降,在工程應用中應避免非對稱L形鋼管混凝土柱在高軸壓比下承載。

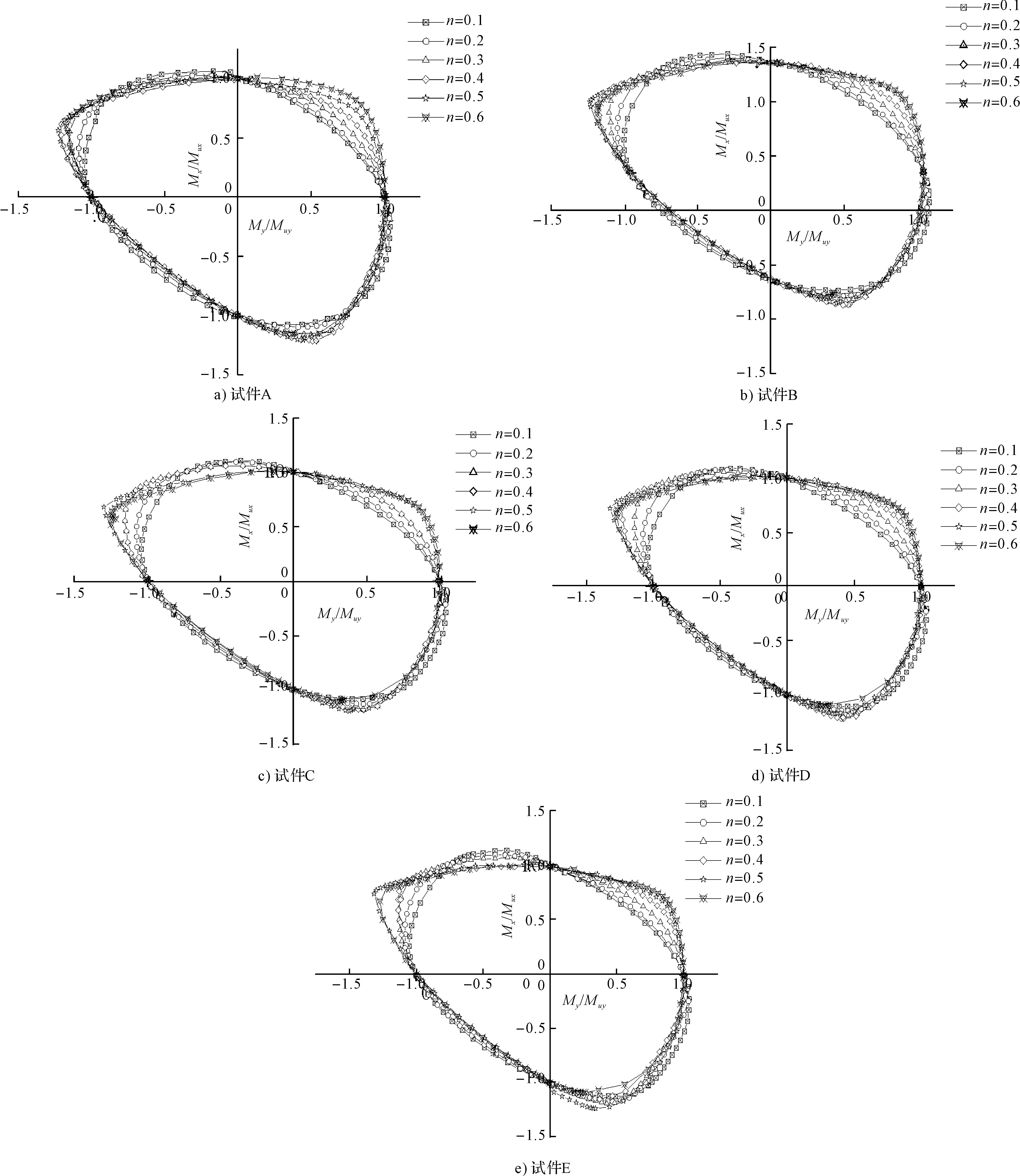
圖4 各試件在不同軸壓比下的N-M相關曲線

3.3 鋼材強度

圖5為不同強度等級鋼材的L形柱的軸力、彎矩相關曲線,由圖5可以看出隨著鋼材屈服強度等級的提高,構件各階段承載力均有所提高。鋼材屈服強度從235 MPa到420 MPa時構件的承載力均勻提高,而當采用屈服強度等級為460 MPa鋼材時,構件的承載力有較大幅度的提高,這說明采用高強度鋼材對構件的承載力提高較為有利。

如圖6所示，L形柱Mx-My相關曲線在不同強度等級鋼材下的形狀是一致的,在尖角位置隨著鋼材強度等級的提高構件的受彎承載力也在略微地提高,原因可能是構件受彎時截面邊緣處的應力最大,有利于外圍的鋼管鋼材強度的發揮,故鋼材強度提高以后構件的抗彎承載力比例會提高。

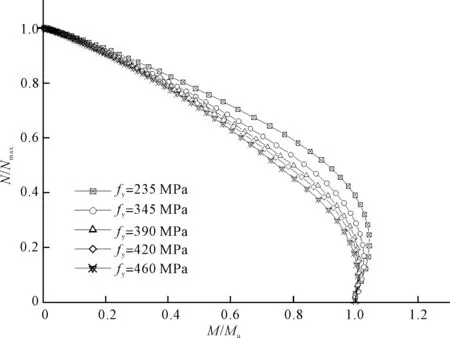
圖5 試件C在45°荷載角下的M-N相關曲線

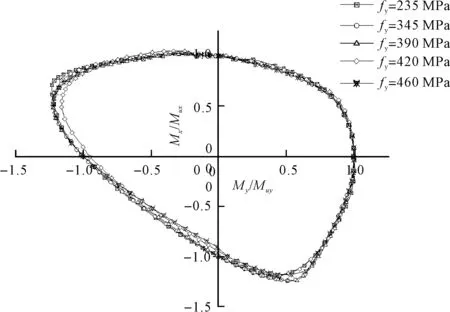
圖6 試件C在軸壓比為0.4時的Mx-My相關曲線

3.4 混凝土強度

圖7為不同強度等級混凝土的L形柱的軸力、彎矩相關曲線。如圖7所示，隨著混凝土強度等級的提高,構件各階段承載力均有所提高,而且承載力提高的幅度也很均勻。相關曲線外凸點隨著混凝土強度等級的提高也在增大,原因是混凝土強度等級的提高,構件的荷載承擔比例也會提高,對壓彎狀態下的抗彎承載力的提高幅度大于對純彎狀態下的提高幅度,故曲線反彎點的橫坐標增加。如圖8所示，L形柱Mx-My相關曲線在不同強度等級混凝土下的形狀是一致的,在尖角位置隨著混凝土強度等級的提高構件的受彎承載力在下降,原因是構件受彎時位于截面中間區域的混凝土對抗彎承載力的貢獻不大,且不考慮混凝土的受拉強度,故混凝土對構件的抗彎承載力比例下降。

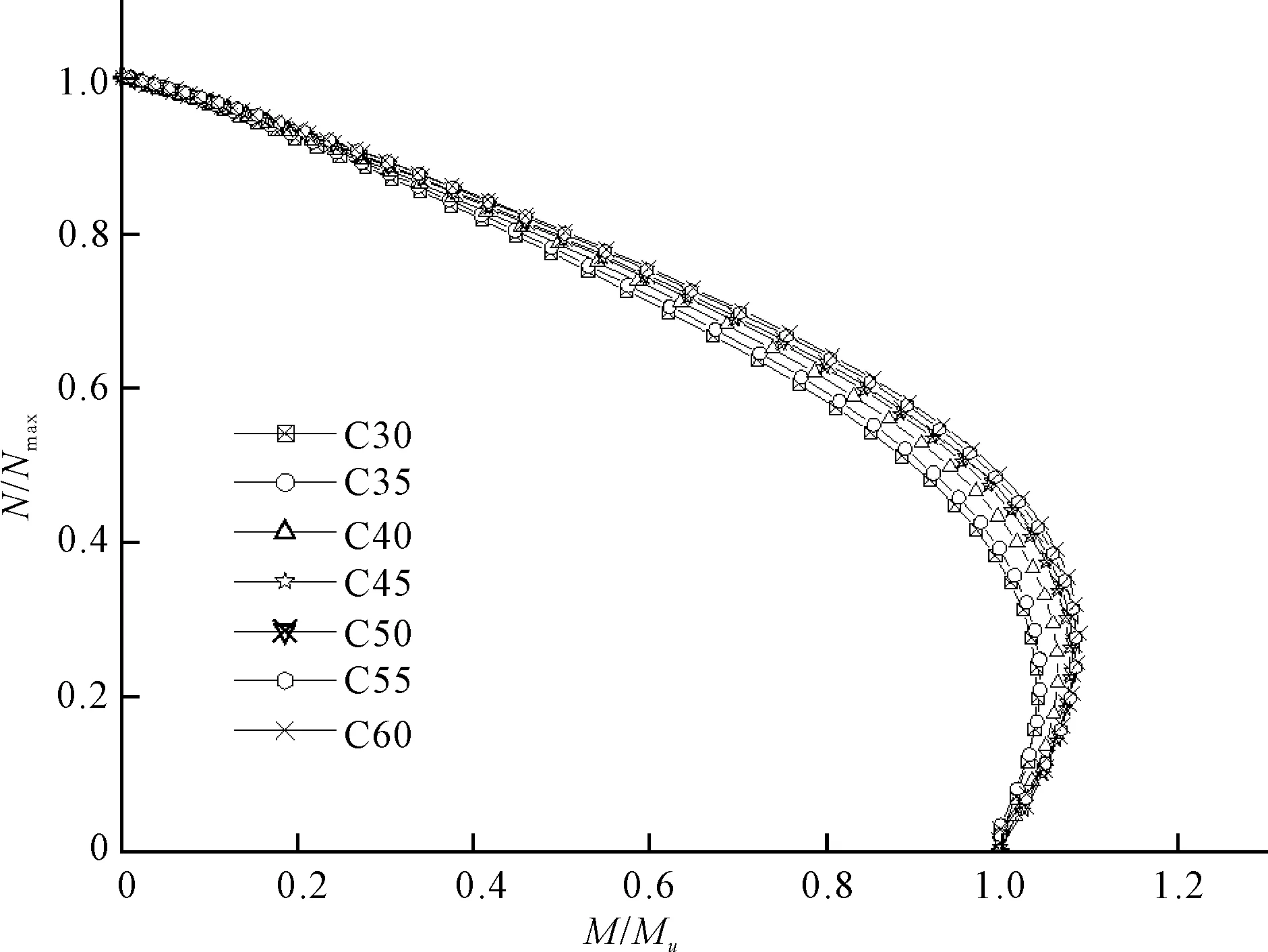
圖7 試件C在45°荷載角下的M-N相關曲線

圖8 試件C在軸壓比為0.4時的Mx-My相關曲線

4 結 語

經分析可得到以下結論：

1)自編程序和有限元分析結果表明,自編程序具有很好的分析精度。

2)荷載角對構件的N-M相關曲線影響較大,角度較小時與鋼柱相似,角度較大時與鋼筋混凝土柱相似。

3)軸壓比對構件的Mx-My相關曲線影響較大,軸壓比較小時Mx與My接近橢圓曲線相關,軸壓比較大時接近線性相關。

4)鋼材屈服強度的提高和混凝土強度的提高與構件的軸壓承載力提高呈正相關,但對于受彎承載力的提高兩者的影響程度則不同。