土壤初始含水率對(duì)微孔陶瓷滲灌入滲特性的影響

陳 璽，董愛紅，趙 笑，蔡耀輝，張 林

(1.西北農(nóng)林科技大學(xué)水利與建筑工程學(xué)院，陜西 咸陽 712100；2.西北農(nóng)林科技大學(xué)水土保持研究所，陜西 咸陽 712100)

地下滴灌是目前應(yīng)用最為廣泛的地下灌溉技術(shù)，但其所用灌水器材質(zhì)大多為塑料且工作水頭較高，不利于可持續(xù)發(fā)展。而微孔陶瓷灌水器是以石英砂、滑石粉和硅溶膠等原料通過一定的工藝燒結(jié)制備而成的新型地下灌水器[1,2]，與常規(guī)滴灌灌水器相比，具有節(jié)能環(huán)保等優(yōu)點(diǎn)，適宜在干旱和半干旱地區(qū)推廣應(yīng)用[3-6]。無壓灌溉作為一種新型的灌水方法，其可行性已通過相關(guān)研究[7-9]得到了驗(yàn)證。趙偉霞等研究[10]發(fā)現(xiàn)無壓灌溉的累計(jì)入滲量與時(shí)間呈冪指數(shù)關(guān)系，土壤入滲率趨于零是無壓灌溉過程結(jié)束的標(biāo)志。無壓灌溉過程中，各層或各深度范圍內(nèi)含水率變化趨勢(shì)相近，濕潤(rùn)體內(nèi)固定點(diǎn)處的含水率在灌水過程中幾乎不發(fā)生變化，灌溉水量的增加只是用來擴(kuò)大濕潤(rùn)體的大小[11]。無壓條件下微孔陶瓷滲灌是以土水勢(shì)為驅(qū)動(dòng)力進(jìn)行的一種主動(dòng)灌溉。在生產(chǎn)實(shí)踐中，由于氣候和灌溉制度的不同，往往需要在不同的土壤初始含水率條件下進(jìn)行灌溉[12]。土壤初始含水率是對(duì)土壤基質(zhì)勢(shì)及濕潤(rùn)鋒處的基質(zhì)勢(shì)梯度產(chǎn)生影響，從而影響土壤水分的入滲[13,14]。在對(duì)涌泉根灌和微潤(rùn)灌溉等[15,16]的研究中發(fā)現(xiàn)，土壤初始含水率對(duì)濕潤(rùn)鋒的運(yùn)移以及水分入滲均有較大影響，土壤初始含水率越大，水分?jǐn)U散速度越快。因此土壤初始含水率是影響水分入滲的關(guān)鍵因素之一。目前針對(duì)微孔陶瓷滲灌入滲特性的研究，主要集中在工作壓力、設(shè)計(jì)流量等系統(tǒng)參數(shù)上[1,17,18]。例如任改萍等[18]研究發(fā)現(xiàn)在微孔陶瓷灌水器灌溉過程中，決定土壤水分累計(jì)入滲量和初始入滲速率的關(guān)鍵因素是供水壓力，并且在各供水壓力水平下，微孔陶瓷滲灌形成的濕潤(rùn)體大小和含水率均能滿足作物根系吸水需求。但對(duì)不同初始含水率條件下微孔陶瓷滲灌的入滲特性研究還較少。

本文以微孔陶瓷灌水器為研究對(duì)象，分析土壤初始含水率對(duì)其累計(jì)入滲量和濕潤(rùn)鋒運(yùn)移距離的影響，探明不同初始含水率條件下微孔陶瓷滲灌的入滲特性，以期為微孔陶瓷灌水器的設(shè)計(jì)及田間應(yīng)用提供一定的科學(xué)依據(jù)。

1 材料與方法

1.1 試驗(yàn)裝置及土壤

試驗(yàn)在西北農(nóng)林科技大學(xué)旱區(qū)節(jié)水農(nóng)業(yè)研究院灌溉水力學(xué)試驗(yàn)大廳進(jìn)行。試驗(yàn)裝置(見圖1)由供水裝置、土箱和微孔陶瓷灌水器組成。供水裝置為能夠提供恒定水頭的馬氏瓶，其橫截面直徑為10 cm，高度90 cm。試驗(yàn)土箱由有機(jī)玻璃制作，尺寸為45 cm×45 cm×75 cm(長(zhǎng)×寬×高)。微孔陶瓷灌水器(見圖2)是由西北農(nóng)林科技大學(xué)中國(guó)旱區(qū)節(jié)水農(nóng)業(yè)研究院自主研制，其結(jié)構(gòu)為圓管形，尺寸為4 cm×2 cm×8 cm(外徑×內(nèi)徑×高)。試驗(yàn)土壤取自陜西渭河三級(jí)階地，將試驗(yàn)土壤風(fēng)干、碾壓、混合后過2 mm篩網(wǎng)后備用。土壤顆粒組成采用激光粒度分析儀(MS2000型，馬爾文，英國(guó))測(cè)定，其中黏粒23.14%、粉粒34.01%、砂粒42.85%。按國(guó)際制土壤質(zhì)地分類標(biāo)準(zhǔn)，試驗(yàn)土壤屬于黏壤土。

圖1 試驗(yàn)裝置示意圖(單位：cm)Fig.1 Layout of the experimental platforms

圖2 微孔陶瓷灌水器Fig.2 Porous ceramic emitter

1.2 試驗(yàn)方法及測(cè)定內(nèi)容

試驗(yàn)土壤按設(shè)計(jì)干容重1.35 g/cm3分層裝入土箱，每層5 cm，共填15層，為使土壤顆粒充分接觸，兩層之間進(jìn)行打毛。土壤表面用塑料薄膜覆蓋，防止土壤水分蒸發(fā)影響試驗(yàn)結(jié)果。微孔陶瓷灌水器水平放置埋于距土壤表面30 cm處，如圖1所示。灌水器兩端用管道連接，一端連接至馬氏瓶，另一端尾部設(shè)有排氣閥(試驗(yàn)開始時(shí)進(jìn)行排氣處理，從而使管道充滿水)。馬氏瓶出水口與水平放置的灌水器中心齊平，即灌水器工作水頭為零。本試驗(yàn)通過采用土壤初始含水率的不同，分別為3%、9%、12%和15%，研究累計(jì)入滲量和濕潤(rùn)鋒運(yùn)移距離隨入滲時(shí)間的變化。試驗(yàn)觀測(cè)時(shí)間為50 h。累計(jì)入滲量通過觀察馬氏瓶的讀數(shù)進(jìn)行換算得出。試驗(yàn)結(jié)束后，以灌水器為中心通過尺子在土箱表面對(duì)所畫濕潤(rùn)峰進(jìn)行量測(cè)。選取圖1中土箱正面的垂直向下和垂直向下的濕潤(rùn)峰運(yùn)移距離和土箱側(cè)面水平方向上的濕潤(rùn)峰運(yùn)移距離，再對(duì)應(yīng)所記錄的時(shí)間，得出濕潤(rùn)鋒運(yùn)移距離隨時(shí)間的變化。

2 結(jié)果與分析

2.1 土壤初始含水率對(duì)累計(jì)入滲量的影響

圖3為不同初始含水率條件下累積入滲量隨入滲時(shí)間的變化曲線。從圖3可以看出，隨著入滲時(shí)間的增加，累計(jì)入滲量的變化率逐漸減小。這是由于無壓條件下，微孔陶瓷灌水器出流的驅(qū)動(dòng)力為土水勢(shì)，即累計(jì)入滲量隨時(shí)間變化規(guī)律是由土水勢(shì)決定[19]。開始入滲時(shí)土壤初始含水率較低，土壤水分主要受到土壤顆粒的吸力(最小值31 atm)和顆粒之間所形成孔隙的毛細(xì)管力(最小值0.3 atm)作用[19]，此時(shí)基質(zhì)吸力非常大，促進(jìn)灌水器出流，故累計(jì)入滲量的變化率較大；隨著時(shí)間的增大，灌水器附近一定范圍內(nèi)的土壤含水率高于田間持水率，土壤中的毛管懸著水達(dá)到最大，毛管力為0，此時(shí)基質(zhì)吸力非常小，從而減緩了灌水器的出流，故隨著入滲時(shí)間的增加，累計(jì)入滲量的變化率逐漸減小。同一時(shí)刻，土壤初始含水率越大，累計(jì)入滲量越小是因?yàn)橥寥莱跏己试酱螅|(zhì)勢(shì)越大即基質(zhì)吸力越小，故累積入滲量越小。為定量分析累計(jì)入滲量隨時(shí)間的變化關(guān)系，對(duì)數(shù)據(jù)進(jìn)行擬合，結(jié)果見表1。

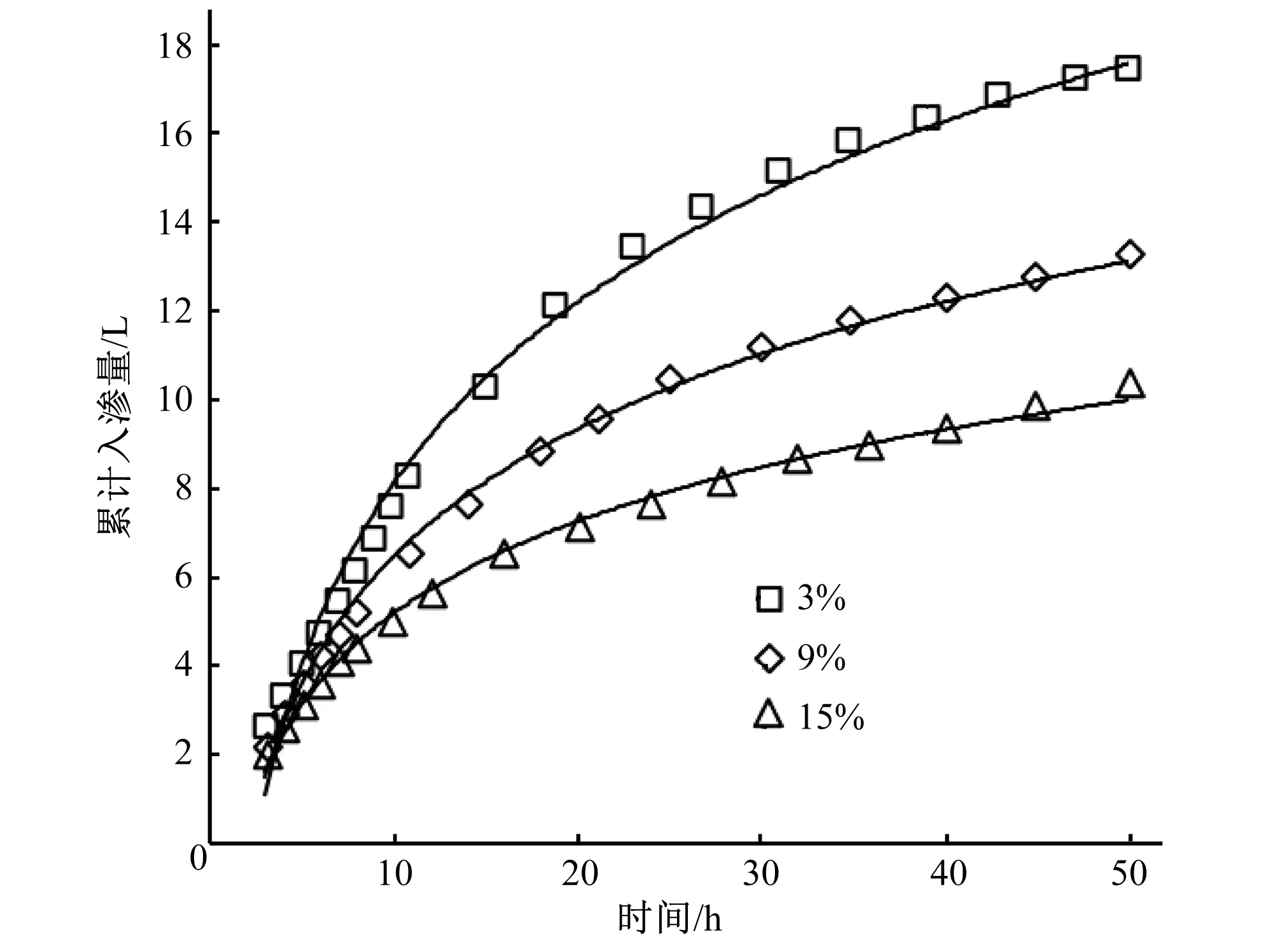
圖3 不同土壤初始含水率下累積入滲量隨時(shí)間的變化Fig.3 Changes of accumulative infiltration by time with different initial soil water contents

表1 不同初始含水率條件下累積入滲量隨時(shí)間變化的擬合公式Tab.1 Fitting results of cumulative infilitration over time at different initial soil water contents

由表1可知，所擬合公式的相關(guān)系數(shù)均達(dá)到0.98以上，可靠性較高，能較好地說明累計(jì)入滲量隨時(shí)間的關(guān)系。在非飽和土壤水分入滲中，土水勢(shì)只需考慮基質(zhì)勢(shì)和重力勢(shì)，且基質(zhì)勢(shì)是土壤含水率的函數(shù)[19]。入滲初期，灌水器周圍的土壤含水率低于田間持水率，土壤水分主要受到土壤顆粒的吸力和顆粒之間所形成孔隙的毛細(xì)管力，二者之和遠(yuǎn)大于所受重力。故在入滲初期，累計(jì)入滲量隨時(shí)間的變化是由基質(zhì)勢(shì)決定，即累計(jì)入滲量隨時(shí)間的變化與土壤初始含水率有關(guān)。隨著時(shí)間的增加，灌水器周圍的土壤含水率高于田間持水率，但此時(shí)形成可自由流動(dòng)的重力水仍是受基質(zhì)勢(shì)控制。因?yàn)檎麄€(gè)土箱內(nèi)的土壤初始含水率均低于田間持水率，隨著時(shí)間的增加，在濕潤(rùn)鋒干濕交界處的土壤水分仍是受到土壤顆粒的吸力和顆粒之間所形成孔隙的毛細(xì)管力的共同作用。故在入滲整個(gè)過程，累計(jì)入滲量隨時(shí)間的變化規(guī)律一直由基質(zhì)勢(shì)決定，而基質(zhì)勢(shì)是土壤含水率的函數(shù)。基于此，提出一種以入滲時(shí)間和土壤初始含水率為自變量、微孔陶瓷滲灌的累計(jì)入滲量為因變量的預(yù)測(cè)模型:

I=f1(θ0) ln(t)-f2(θ0)

(1)

f1(θ0)、f2(θ0)由表1對(duì)應(yīng)的系數(shù)得出：

(2)

(3)

綜上所述，微孔陶瓷滲灌的累計(jì)入滲量預(yù)測(cè)模型為:

(4)

公式(4)是在灌水器長(zhǎng)度為8 cm時(shí)擬合出來，故也可知單位長(zhǎng)度下累計(jì)入滲量和土壤初始含水率與入滲時(shí)間的關(guān)系。在實(shí)踐中，此模型可根據(jù)作物生長(zhǎng)周期所需水量和土壤初始含水率，來確定在作物生長(zhǎng)周期內(nèi)灌水量是否能得到滿足其生長(zhǎng)需要。如若不能，可通過單位長(zhǎng)度下累計(jì)入滲量與初始含水率和時(shí)間的關(guān)系推求灌水器長(zhǎng)度，使其達(dá)到最優(yōu)。

為檢驗(yàn)?zāi)Ｐ偷目煽啃裕渲猛寥莱跏己蕿?2%的土樣，按相同的標(biāo)準(zhǔn)進(jìn)行試驗(yàn)，選取8個(gè)時(shí)間點(diǎn)進(jìn)行分析，將其實(shí)測(cè)值和模型擬合值進(jìn)行對(duì)比分析，結(jié)果見表2。

表2 累積入滲量實(shí)測(cè)值與模型擬合值Tab.2 Measured and model fitted values of cumulative infiltration

由表2可知，累積入滲量實(shí)測(cè)值和模型擬合值的相對(duì)誤差均在±5%范圍以內(nèi)，說明該模型對(duì)無壓條件下微孔陶瓷滲灌的累積入滲量預(yù)測(cè)精度較好。

2.2 土壤初始含水率對(duì)濕潤(rùn)鋒運(yùn)移距離的影響

圖4為在不同初始含水率條件下，垂直向下濕潤(rùn)鋒運(yùn)移距離、水平方向濕潤(rùn)鋒運(yùn)移距離和垂直向上濕潤(rùn)鋒運(yùn)移距離隨入滲時(shí)間的變化曲線。從圖4可看出，在3個(gè)方向上都具有相同的規(guī)律：同一入滲時(shí)刻，土壤初始含水率越大，運(yùn)移距離越大。這是由于土壤初始含水率越高，土壤的儲(chǔ)水能力越小，土體不能夠吸持更多的水分，從而更利于濕潤(rùn)峰的推進(jìn)。同一土壤初始含水率下，不同方向上運(yùn)移距離隨時(shí)間也不相同。為了定量分析土壤初始含水率對(duì)濕潤(rùn)鋒運(yùn)移距離的影響，用冪函數(shù)進(jìn)行擬合，結(jié)果見表3。

圖4 不同初始含水率下濕潤(rùn)峰運(yùn)移距離隨時(shí)間變化曲線Fig.4 The curve of the migration distance of wetting peaks with time at different initial moisture content

表3 濕潤(rùn)峰運(yùn)移距離隨時(shí)間變化的擬合關(guān)系Tab.3 The relationship of the migration distance of wet front with time

從表3可發(fā)現(xiàn)，所擬合公式的相關(guān)系數(shù)均達(dá)到0.99以上，可靠性較高，能較好地說明運(yùn)移距離隨時(shí)間的關(guān)系。在同一方向上，不同初始含水率下運(yùn)移距離的冪函數(shù)中的指數(shù)相差不大，可假設(shè)指數(shù)對(duì)其影響不大。取其平均值，建立垂直向下濕潤(rùn)鋒運(yùn)移距離隨時(shí)間的方程：

x(t,θ0)=f3(θ0)t0.381 3

(5)

垂直向上濕潤(rùn)鋒運(yùn)移距離隨時(shí)間的方程：

S(t,θ0)=f4(θ0)t0.304 1

(6)

水平方向濕潤(rùn)鋒運(yùn)移距離隨時(shí)間的方程：

L(t,θ0)=f5(θ0)t0.442 3

(7)

將上面方程公式(5)～(7)結(jié)合圖4的數(shù)據(jù)重新擬合可得表4。

表4 濕潤(rùn)峰運(yùn)移距離隨時(shí)間變化的擬合模型Tab.4 The model of the migration distance of wet front over time

表4的相關(guān)系數(shù)均達(dá)到0.97以上，說明對(duì)指數(shù)取平均值影響不大，故之前假設(shè)成立。因此能較好地說明濕潤(rùn)鋒運(yùn)移距離隨時(shí)間的關(guān)系。由表4的數(shù)據(jù)可得出：

(8)

(9)

(10)

垂直向下運(yùn)移距離方程：

(11)

垂直向上運(yùn)移距離方程：

(12)

水平方向運(yùn)移距離方程：

(13)

為檢驗(yàn)?zāi)Ｐ偷目煽啃裕谕寥莱跏己蕿?2%條件下，按相同的標(biāo)準(zhǔn)進(jìn)行試驗(yàn)，選取8個(gè)時(shí)間點(diǎn)進(jìn)行分析，將其實(shí)測(cè)值和模型擬合值進(jìn)行對(duì)比分析，結(jié)果見表5。

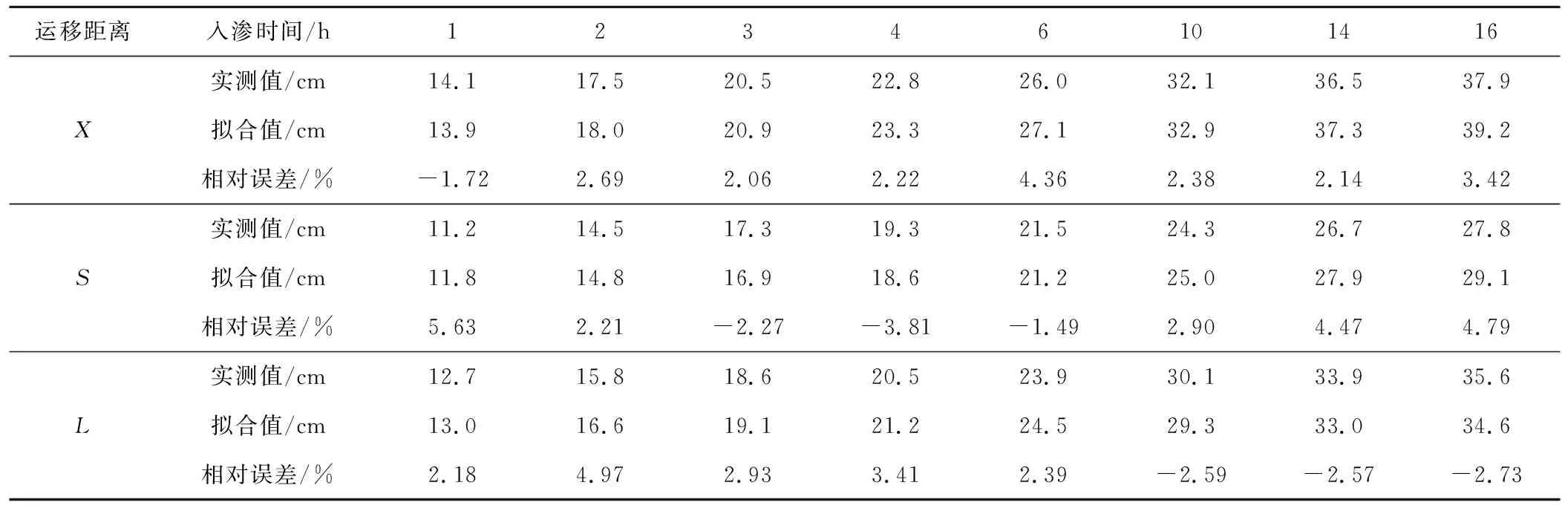
表5 濕潤(rùn)鋒運(yùn)移距離實(shí)測(cè)值與模型擬合值對(duì)比Tab.5 Comparison of measured values of wet front transport distance with model fitting values

由表5可知，水平方向濕潤(rùn)鋒運(yùn)移距離、垂直向下濕潤(rùn)鋒運(yùn)移距離和垂直向上濕潤(rùn)鋒運(yùn)移距離的實(shí)測(cè)值和模型擬合值相對(duì)偏差均在±6%圍以內(nèi)，說明用該模型對(duì)無壓條件下微孔陶瓷灌水器入滲的各方向濕潤(rùn)鋒運(yùn)移距離進(jìn)行預(yù)測(cè)精度較好。

3 結(jié) 語

(1)建立了以土壤初始含水率和入滲時(shí)間為自變量，累計(jì)入滲量為因變量的預(yù)測(cè)模型。并用土壤初始含水率為12%的試驗(yàn)數(shù)據(jù)對(duì)模型進(jìn)行驗(yàn)證，結(jié)果表明模型具有較好的精度，可以預(yù)測(cè)不同初始含水率下微孔陶瓷滲灌的累積入滲量。此模型可根據(jù)作物生長(zhǎng)周期所需水量和土壤初始含水率，來確定在作物生長(zhǎng)周期內(nèi)灌水量是否能滿足其生長(zhǎng)需要。如若不能，可通過單位長(zhǎng)度下累計(jì)入滲量與初始含水率和時(shí)間的關(guān)系推求灌水器長(zhǎng)度，使其達(dá)到最優(yōu)。

(2)建立了不同初始含水率條件下濕潤(rùn)峰運(yùn)移距離隨時(shí)間變化的模型。并對(duì)模型進(jìn)行了驗(yàn)證，結(jié)果表明 模型具有較好的精度，可以預(yù)測(cè)不同初始含水率條件下微孔陶瓷滲灌濕潤(rùn)鋒運(yùn)移距離隨時(shí)間變化過程。