地震動強度指標選取對IDA結果的影響
唐 月 ,李 丹
(安徽新華學院,土木與環境工程學院,安徽 合肥 230000)
1 引言
增量動力分析(IDA)方法是一種用于評測建筑結構抗震性能的動力參數分析方法。增量動力分析方法最早是在1977年由Bertero[1]提出,后來經Cornell和Vamvatasikos[2]等學者進行進一步的發展與研究,并且在2000年已經被FEMA350[3],FEMA351[4]采用作為建筑結構整體抗倒塌能力分析的一種方法。IDA方法是一種向量化寬范圍地變量參數非線性動力分析方法,可以分析出建筑結構在地震動作用時的抗倒塌能力、結構性能變化等。
2 IDA方法
增量動力分析(IDA)方法是將單一的時程分析方法,通過對地震動強度幅值進行遞增式調整從而獲得增量式時程分析,因此也被稱為“動力推覆分析”。增量動力分析方法將地震動強度按等步長法、變步長法等方法獲得一定的比例系數,計算得到不同幅值的地震動強度,結構在其作用下,進行非線性動力時程分析,得到對應的結構性能參數,將此結構性能參數DM數值與地震動強度值IM數值進行連線繪制,即為IDA曲線。
本文分別取地震動峰值加速度、阻尼比為5%的結構基本周期對應的加速度譜值、地震動峰值速度作為地震動強度IM值,結構性能參數取最大層間位移角作為DM值,進行IDA計算分析。
3 算例分析
3.1 工程概況
本文設計一棟4層鋼筋混凝土框架結構,此結構模型按Ⅱ類第二組場地,設防烈度8度設計計算。結構總共4層,各層高均為3.6m,樓面恒荷載標準值為5KN/m2,樓面活荷載標準值為2 KN/m2,建筑結構布置如圖1所示。結構按PKPM程序軟件進行計算設計,采用MIDAS GEN進行建模和計算分析。
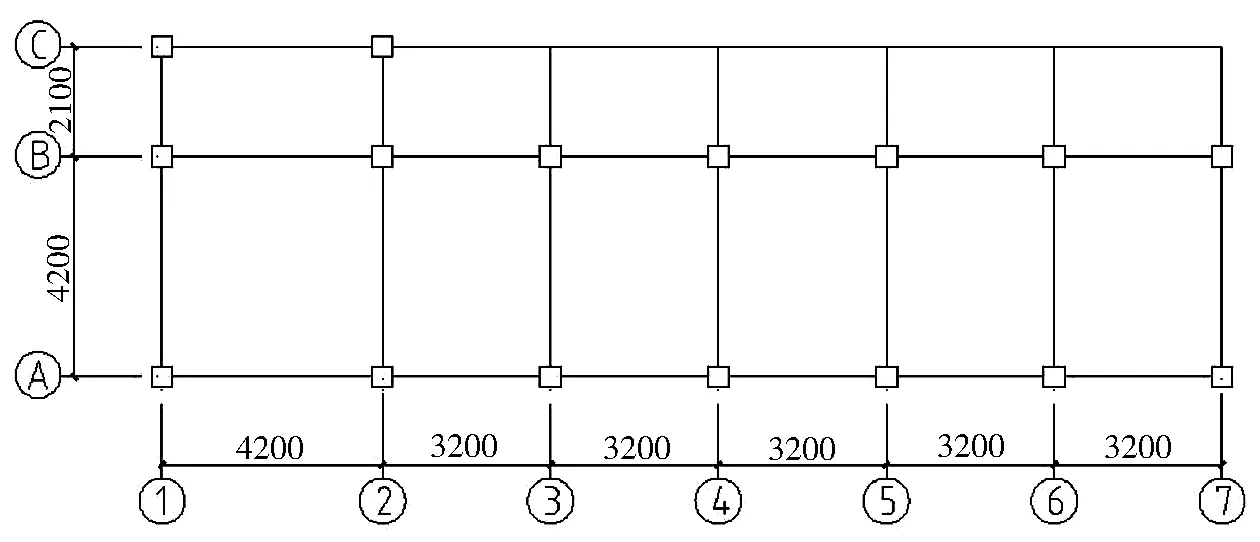
圖1 結構平面布置圖Fig.1 Layout plan of structure
選取輸入八條地震動記錄作用于結構模型,分別按采用峰值加速度PGA、結構自振周期的5%阻尼比對應的譜加速度譜值Sa(T1,5%)、峰值速度PGV作為不同的地震動強度參數IM值,最大層間位移角θmax作為結構性能參數DM值,按變步長法計算分析出對應的三組IDA曲線。計算所用的地震動記錄如表1所示。
表1計算所用地震動記錄
Table.1thegroundmotionrecordsused
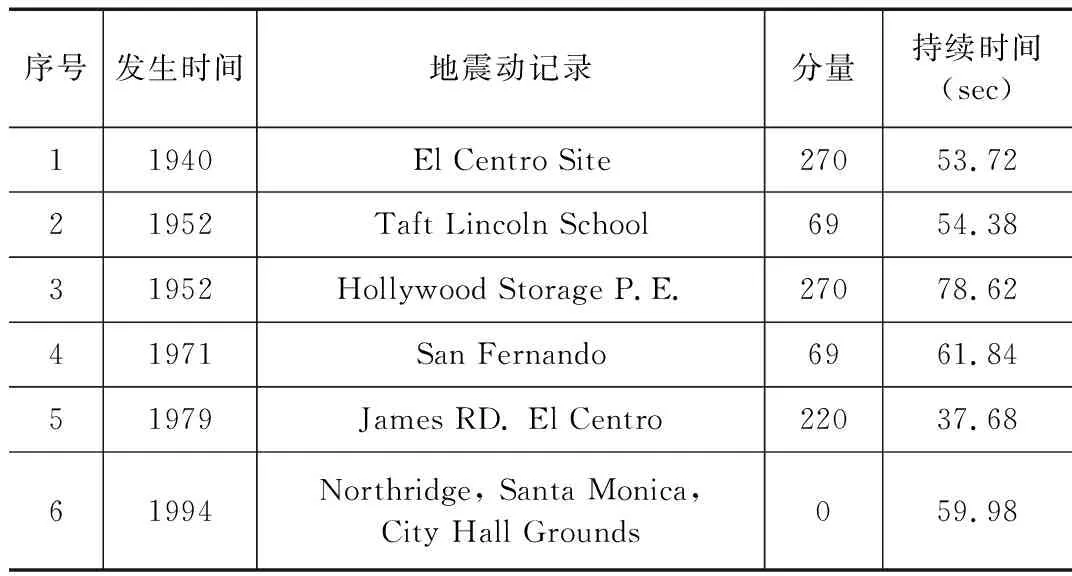
序號發生時間地震動記錄分量持續時間(sec)11940El Centro Site27053.7221952Taft Lincoln School6954.3831952Hollywood Storage P.E.27078.6241971San Fernando6961.8451979James RD. El Centro22037.6861994Northridge, Santa Monica, City Hall Grounds059.98

序號發生時間地震動記錄分量持續時間(sec)71989Loma Prieta, Oakland Outer Wharf27039.9881966Parkfield Cholame,Shandon4026.18
3.2 計算擬合IDA曲線
使用MATLAB軟件對三組IDA曲線數值用三次樣條插值方法進行分析擬合,計算出的三組不同IM參數值的IDA曲線,如圖2。對三組數值結果按16%、50%、84%繪制分位IDA曲線圖,如圖3所示。
3.3 IDA結果分析討論
按FEMA[5]計算規則,在IDA曲線斜率處于彈性階段20%Ke時,即為建筑結構處于不倒塌的極限狀態點(CP點),而斜率剛開始出現較大變化時,即框架結構取最大層間位移角為1%時,定義為不修可繼續使用狀態點(IO點)。在三組分位IDA曲線標出對應IO、CP狀態點,如圖3。三組16%、50%、84%分位IDA曲線狀態性能點如表2所示。
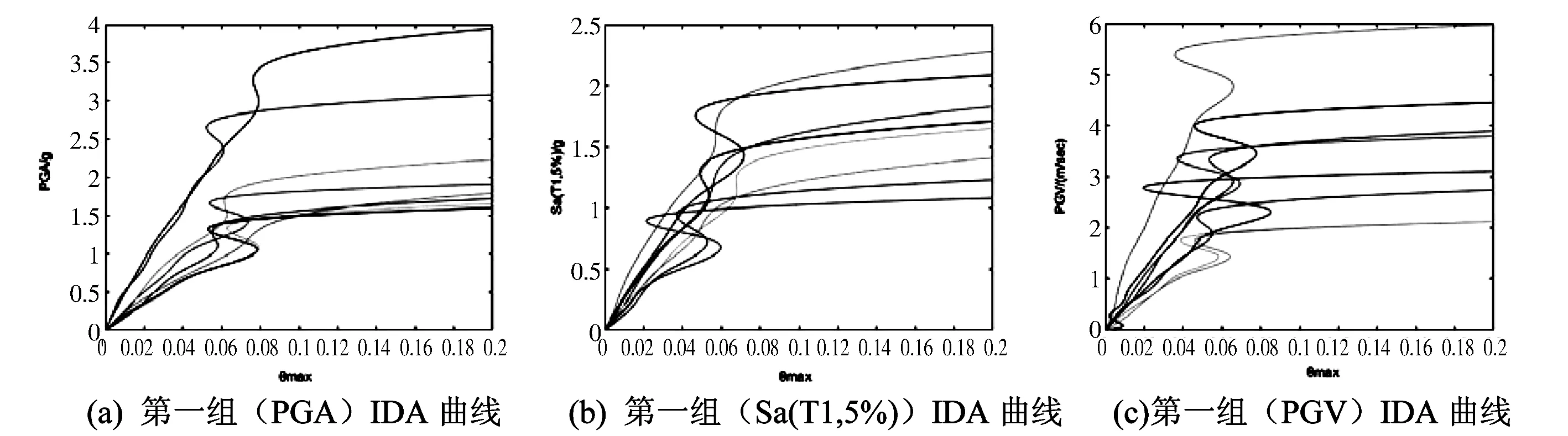
圖2 不同強度指標的IDA曲線Fig.2 IDA curves of different intensities index
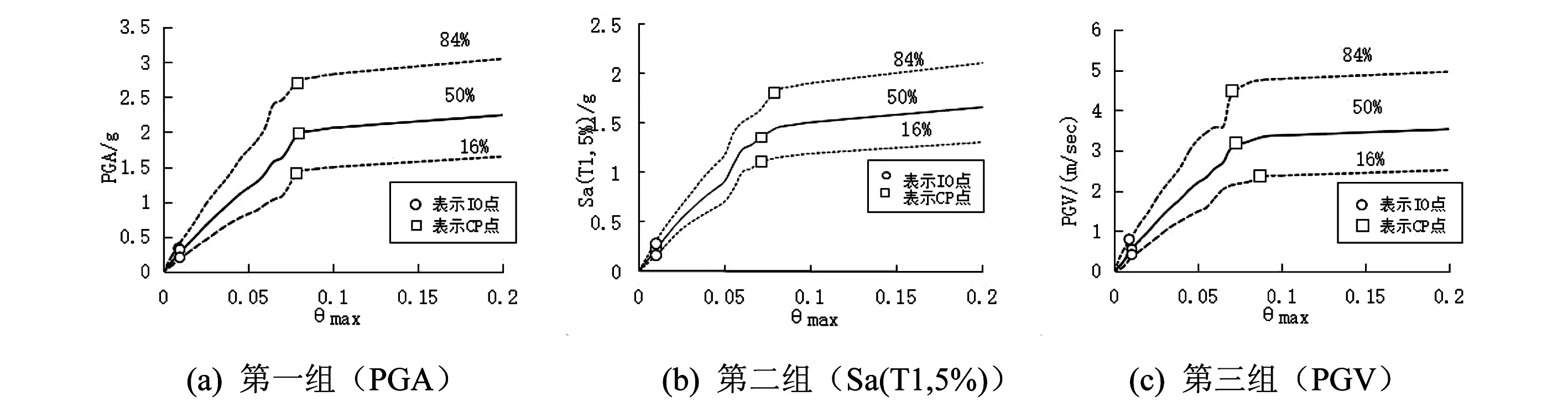
圖3 16%、50%、84%分位IDA曲線Fig.3 16、50and 80% fractile IDA curves
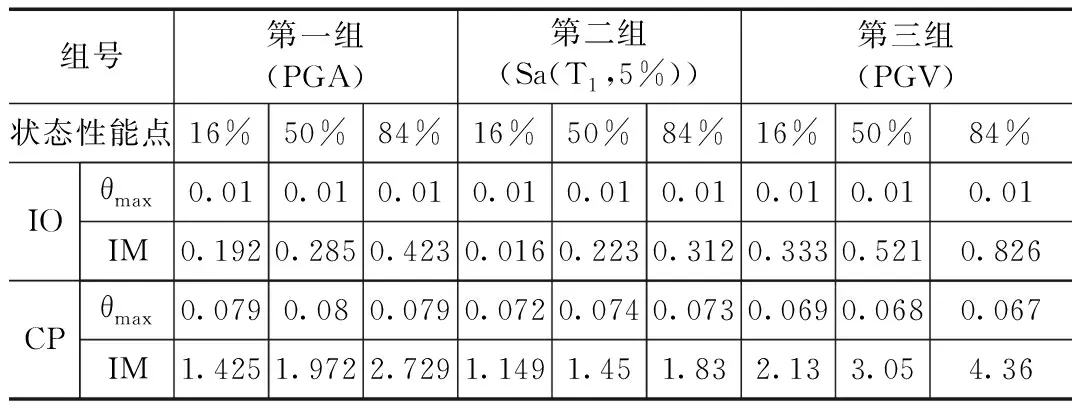
表2 IDA曲線狀態性能點Table.2 Performance points of IDA curve
在圖3中,第一組曲線數值的離散性最小,第三組的分位IDA曲線數值相比第一、二組數值離散性最大,有較大的偏差。在表2中,在16%、50%、84%分位曲線上,第二組的IO點均最小,第一組數值較接近第二組數值。對于結構不修仍可繼續使用狀態的IO點,第二組的分析結果最為保守。對于結構不倒塌極限狀態點CP點,在地震動達到1.149g時,在第二組分析中則最早可能出現結構倒塌。而當結構在地震動作用下,最大層間位移角達到0.067時,第三組的分析中則會最早可能出現結構倒塌。第一組數值分析結果向第二組結果較相近。
按ATC-63[6]提出的抗倒塌儲備系數(CMR)分析建筑結構的抗倒塌能力。CMR即反應出結構的設防需求和實際抗震倒塌能力的儲備指標。可以造成50%建筑結構倒塌概率的地震強度指標,即為結構的抗倒塌能力,計算方式如式1所示:
CMR=IM50%倒塌/IM設防大震
(1)
式中:IM設防大震——規范建議下的大震地震動強度指標。
按上式計算出三組不同地震動強度指標作為IM數值時的倒塌儲備系數,如圖4所示。
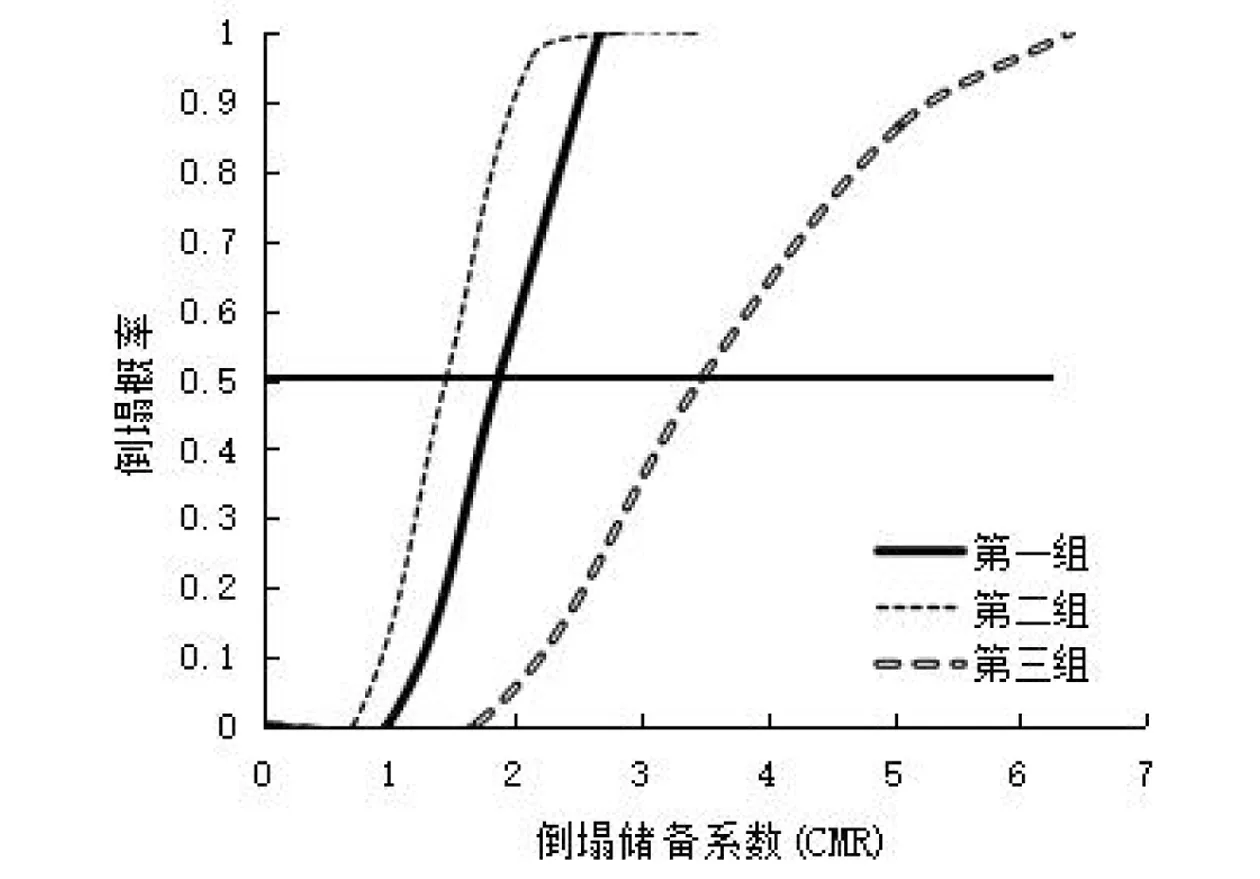
圖4 倒塌概率曲線Fig.4 Collapse possibilities of frames
在圖4中,三組不同的地震動強度指標作為IM系數時,其所對應的結構抗倒塌儲備系數為:第一組CMR等于1.87,第二組CMR等于1.44,第三組CMR等于3.47。其中評測分析出的第二組抗倒塌儲備系數數值最小,即隨地震動強度增大,以Sa(T1,5%)做IM參數時,評測結構最早出現結構倒塌情況。第一組CMR曲線數值向第二組曲線靠攏,第三組的抗倒塌儲備系數明顯大于第一、二組,并隨著地震強度增加,數值差別越明顯,按第三組的評測結果,結構具有較好的抗倒塌性。
4 結語
本文以鋼筋混凝土框架結構模型為例,分別采用峰值加速度、結構自振周期的5%阻尼比對應的譜加速度、峰值速度作為不同的地震動強度參數IM值,分析了三組不同IM參數值對IDA結果的影響,得出以下結論:
(1)以三種不同參數IM值計算分析出的IDA結果都有一定的差異,以譜加速度、峰值加速度、峰值速度為參數值,分析結果的離散性依次增大,而以譜加速度為參數值可以獲得最小離散性的IDA結果。
(2)對于結構在塑性抗倒塌階段,以峰值速度為參數時,結構有比較好的抗倒塌性,而以譜加速度為參數時,可以得到結構最保守的分析結果。
(3)本文采用最大層間位移角作為性能參數值,限于篇幅,當選擇其他結構性能參數時地震動強度選取對于IDA結果的影響,還有待于進一步研究。

