基于非線性回波包絡模型的超聲波飛行速度測量方法*

王曉偉， 張寶峰， 高玉林， 焦英魁， 李志偉， 朱均超

(1.天津理工大學 天津市復雜系統控制理論及應用重點實驗室，天津 300384；2.天津大學 精密儀器與光電子工程學院，天津 300072； 3.秦皇島視聽機械研究所，河北 秦皇島 066000)

0 引 言

海水聲速剖面儀是測量海水中聲波傳播速度的儀器，為單波速測深儀、多波速測深儀等提供實時海水聲速值，是海洋聲吶儀器應用廣泛的儀器。聲速測量方法中時差法[1]是多數聲速剖面儀所采用的方法。目前，在測量海水聲速技術中，差分飛行時間法[2]得到較快發展。超聲波飛行時間是測量海水聲速的重要參數。近年來，多位學者對此進行了研究，比較典型的測量方法有互相關法、閾值法、非線性回波包絡模型估計法[3～5]等。非線性回波包絡模型方法具有運算量小、實時性好，可以實現更高精度測量。非線性回波包絡模型參數估計屬于一類最優化問題。目前為了解決超聲波多參數識別問題，智能優化算法得到廣泛應用，如高斯牛頓法[6]、遺傳算法[7]。前者應用于超聲波非線性回波模型參數求解，其計算精度不高，參數初值設置不當，易使實際數據擬合程度較低，因此在實際應用中有很大的局限性；利用遺傳算法進行參數估計，在解決搜索問題時速度較慢，且收斂結果精度較低。

針對上述問題，采用改進粒子群優化算法對非線性回波包絡模型參數進行優化，確定超聲波飛行時間。該方法對接收換能器輸出超聲波回波信號進行高速采樣和多參數非線性曲線擬合后，采用改進的粒子群優化算法對非線性回波包絡模型參數進行優化，獲得相應超聲波傳播時間參數最優值。

1 基于非線性回波包絡模型估計聲速測量方法

1.1 測量原理

差分飛行時間法測量原理如圖1，發射換能器A與接收換能器B之間的初始距離為L，超聲波飛行時間t1，通過水平調節接收換能器B，移動Δs，接收換能器A與發射換能器B之間的距離為L+Δs，再次施加相同周期相同頻率的激勵信號，超聲波的飛行時間t2。

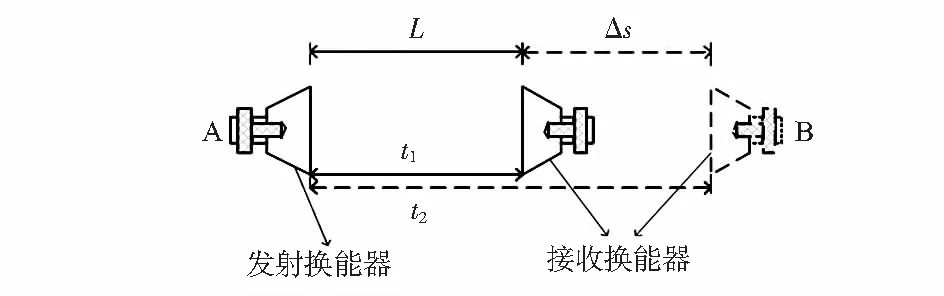
圖1 測量原理示意

由聲速計算公式v=L/t，可表示

(1)

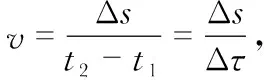
1.2 非線性回波包絡模型建立

依據超聲波換能器工作原理，換能器的振子受接收超聲波聲壓作用而受迫振動，超聲波信號結束，振子進行阻尼衰減振動，換能器接收的超聲波信號可模擬成阻尼正弦波[8]

A(t)=B(t)sin(2πfc(t-τ)),t≥τ

(2)

(3)

式中si(θ)為回波包絡信號模型，β為幅值，τ為到達時間，A(t)為接收回波信號，θ=[βτTα]為非線性回波包絡模型參數向量,fc為超聲波的頻率。

用上述回波包絡模型擬合實際回波包絡信號，實際回波包絡通過希爾伯特變換獲得。根據實際回波包絡信號，對回波包絡模型參數向量θ進行估計獲取回波到達時刻。

1.3 構造最小二乘函數

本文采用最小二乘法對非線性回波模型參數進行估計，構建最小二乘目標函數，采用改進粒子群優化算法進行優化，獲得超聲波的飛行時間。建立最小二乘目標函數

(4)

式中x(i)為通過實驗測得的回波包絡數據，si(θ)為第i次迭代得到非線性模型參數向量對應的回波包絡函數值。因此，其實質是將估計參數模型問題轉化為非線性的最小二乘目標函數優化問題，即估計目標函數f(θ,ti)取盡可能小值時，對應θ值視為最佳參數，即min{f(θ)}→θ。

由文獻[9]可知，回波上升沿由換能器壓電陶瓷振子的阻尼因子決定的，不易受其他因素影響，因此對回波包絡上升沿部分數據進行參數估計能夠提高運算精度。

待估計參數沒有特定取值區間，因此針對這類問題迭代搜索算法在優化求解上具有優勢，鑒于搜索算法的快速性與準確性，粒子群優化(particle swarm optimization,PSO)算法迭代過程簡單且容易實現，基本粒子群算法迭代過程中收斂速度快，為避免出現早熟現象，對基本粒子群進行改進，提高算法的收斂性，求得參數的最佳值。

2 改進粒子群優化算法估計最優飛行時間

標準粒子群優化算法[10]更新速度和位置的過程中，慣性權重是重要的參數，其作用有效控制算法收斂，避免早熟。慣性權重較大，利于提高算法的全局搜索能力；慣性權重較小，有利于算法的局部搜索能力，從而控制算法的收斂。慣性權重的合理選取較大程度上決定了算法的執行結果。目前，慣性權重的研究有多種變化策略[11]本文采用動態確定權值w，其值在非線性遞減的基礎上實現同代粒子選取方案，進而改善算法的收斂性。設wmax為權重系數最大值，wmin為權重系數最小值，t為當前的迭代次數，tmax為算法允許的最大迭代次數，則非線性遞減慣性值為

wt=(wmax-wmin)(t/tmax)+

在地鐵防水作業中最需要關注的就是分段澆筑出現的接縫滲漏水治理工作。現階段，我國在施工中防水的方式主要是利用鍍鋅鋼板的止水帶來進行防水，在工程施工中鍍鋅鋼板止水帶是最普遍的一種的材料。進行澆筑混凝土下層的位置時，其中預埋鍍鋅鋼板的小部分就會外漏在表面，進行再次澆筑混凝土時再一起澆筑，可以把外面的壓力水進行阻止。另外，鍍鋅鋼板止水帶防水技術有下面幾種：變形施工縫防水、施工縫防水和澆帶防水等。由于鍍鋅鋼板止水防水技術存在不足，是因為止水帶在接頭位置太多，封閉性就無法達到施工的要求。

2(wmin-wmax)(t/tmax)+wmax

(5)

式(5)為一條開口向上的拋物線，取wmax=0.9，wmin=0.1。當t=0時，w值為wmax；當t=tmax時，w值隨凹函數非線性遞減為wmin。利用式(5)計算出每一代慣性權重wt(t=1,2,…,tmax)，選擇三角形概率分布為第t代中各個粒子隨機選擇權值。第t代的隨機權值選擇的三角形概率分布密度數是以點(wmax，0)，(wmin，0)，(wt,2/(wmax-wmin))為頂點的折線。第t代中，每個粒子隨機選擇的慣性權值為

xi=G1(ui)，i=1,2,…,M

(6)

式中u1,u2,…,uM為服從(0,1)上均勻分布的隨機變量 所取得隨機數，G0(u)(t=0),Gt(u)(t>0)分別為

(7)

(8)

根據上述改進方案，改進的粒子群優化算法的計算步驟為：

1)初始化算法的參數。搜索空間維數D，最大迭代次數K。初始化粒子群中個體的初始位置和初始速度。

2)計算群體中各個粒子初始適應值，標記初始個體粒子經歷最好位置及優化個體極值，并標記整個粒子群的歷史最優位置和優化全局極值。

3)判斷算法是否滿足迭代終止條件，如果滿足，轉向步驟(7)；否則，執行步驟(4)。

5)計算每個粒子的適應度，如果新粒子的適應度值優于當前粒子的個體極值，則新粒子設為個體極值點，若所有粒子的個體極值中最佳的優于當前全局極值，則將該個體極值點設為全局極值點。

6)判斷算法是否滿足迭代終止條件，如果不滿足，轉向步驟(4)；否則，執行步驟(7)。

7)得到的全局極值點為最優解。

3 實驗與結果分析

3.1 超聲波傳播時間測量系統結構

本文測試系統結構如圖2所示，選用信號發生器作為激勵源，計算機控制信號發生器發射一組正弦激勵信號，經發射換能器轉換為超聲信號經過液體傳到接收換能器，接收換能器將接收到聲信號轉換為電信號，進行采集、存儲，將結果送入計算機進行處理。

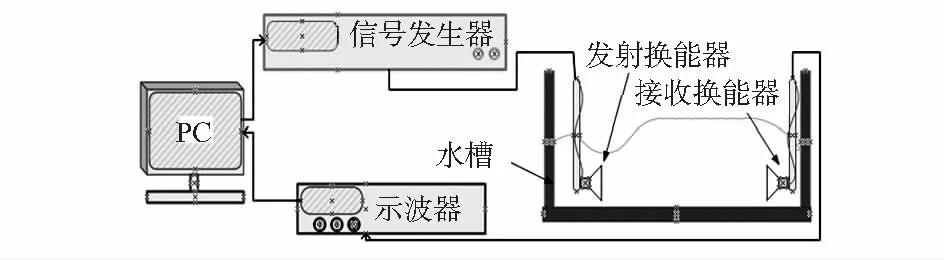
圖2 聲速測量實驗系統結構

3.2 超聲波傳播時間測量實驗

海水聲速隨溫度、鹽度以及壓力變化，在常壓下，純水聲速僅與溫度有關。因此，本文實驗在常壓下且純水中完成，避免鹽度及壓力變化對聲速測量值的影響。通過支架固定超聲波發射及接收換能器，浸沒在注滿純水的恒溫水槽中，精密電控位移平臺控制接收換能器移動的距離，其重復定位精度小于2 μm，可精確測量位移差。使用信號發生器作為信號源，接收信號由示波器進行采集。

計算出當前環境純水的聲速值。為了對比超聲波飛行速度測量的準確性，在恒溫水槽中貼近接收換能器處放置一臺精度比較高的聲速儀，精度可達±0.017 m/s，將本文計算聲速值與聲速儀實測值進行對比。

3.3 實驗結果與驗證

實驗選取20,25,30 ℃ 3個恒溫點，溫度在2 min內波動小于0.003 ℃。選取τmin=78 μs，τmax=90 μs，改進粒子群優化算法的最大種群規模設為50個，最大迭代次數為200次，根據式(5)，設置慣性權重，wmin=0.1，wmax=0.9,參數向量β的范圍為(1,10)V，T,α的取值范圍分別為(50,90)μs，(1,3)，τ視距離變換而變換。

在提取包絡中，確定包絡信號的上升沿的數據，通過包絡模型B(t)=β((t-τ)/T)αe-(t-τ/T)對回波包絡上升沿進行擬合，利用改進的粒子群優化算法和粒子群優化算法分別對包絡模型特征參數向量θ進行優化。

可知，粒子群優化算法的收斂率為80 % ，而改進的粒子群優化算法的收斂率可達到99 %；粒子群優化算法的平均迭代次數(112)比改進的粒子群優化算法(78)高，表明改進的粒子群優化算法的收斂速度)比粒子群優化算法高。2種算法回波包絡模型與實際接收信號包絡的擬合效果如圖3，可以看出實際接收回波包絡上升沿與回波包絡模型相符合。但改進的粒子群優化算法擬合最為準確，其上升沿相對于粒子群優化比較陡，其測量時間更加準確。

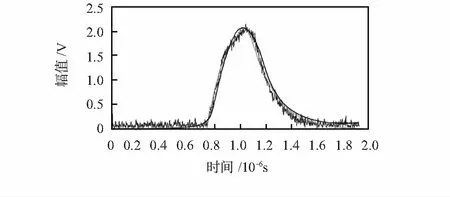
圖3 超聲波接收信號擬合效果

為了驗證本文方法計算超聲波聲速的有效性，計算完一組超聲波的TOF，信號發生器發射下一組波形，每10組計算1次t1平均值作為最終結果。精密電控位移平臺調整接收換能器位置為Δs，重復上述步驟計算t2。25 ℃測量數據如表1所示。計算實際測得聲速為1 497.196 m/s,重復上述操作過程，調節恒溫水槽溫度為29.881,20.082 ℃，分別記錄兩臺聲速儀測量聲速數據及計算本文方法測量的聲速數值,可知，溫度對超聲波飛行速度的影響隨著溫度增大而大。在24.958 ℃恒溫點時，本文方法測量聲速值與參考聲速儀測量差為0.003 m/s，在其他恒溫點測量差為0.15 m/s。

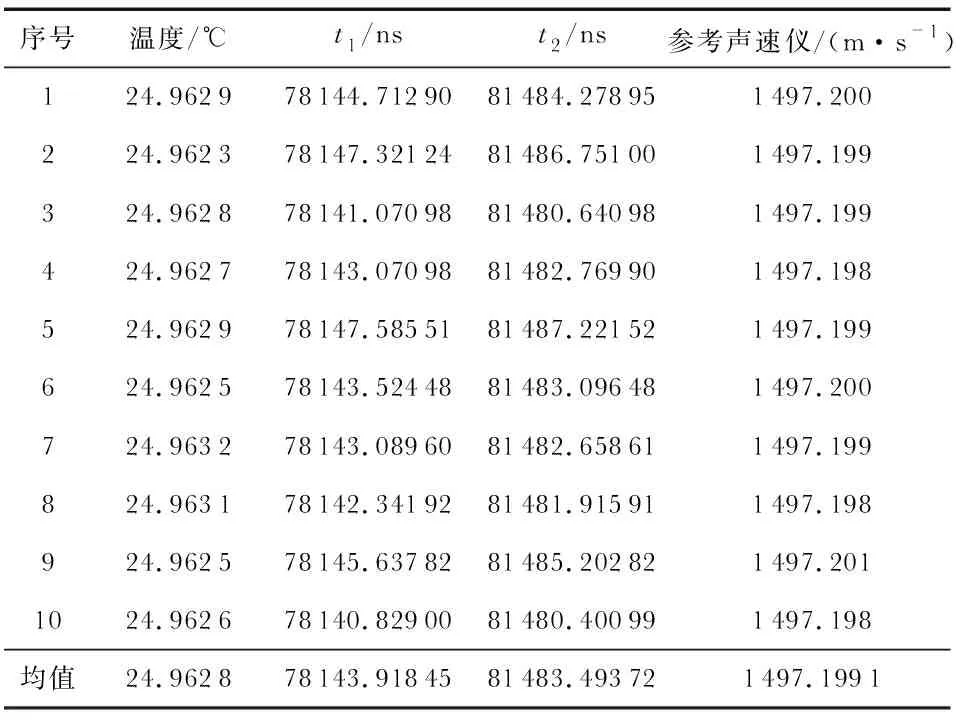
表1 25 ℃ 實驗測試數據

4 結 論

本文基于超聲波飛行時間與速度關系，通過改進粒子群優化算法對回波包絡上升沿擬合，獲得超聲波在恒溫水槽中固定距離下的飛行時間，從而獲得超聲波飛行速度。實驗結果證明基于非線性回波模型超聲波飛行速度的測量方法可行，對今后的海水聲速測量系統具有重要的實用價值。