基于CFX的百葉窗開度對間接空冷散熱器影響的研究
王晗昀
(南京市市政設計研究院有限責任公司, 南京 210008)
間接空冷系統(tǒng)利用散熱器實現(xiàn)循環(huán)水與空氣表面換熱,具有節(jié)水省電、換熱效率高、單位煤耗低等特點,在我國北方地區(qū)逐漸得到廣泛應用[1]。然而,間接空冷塔的運行易受外界環(huán)境干擾,常出現(xiàn)夏季冷卻出力不足、冬季散熱器凍結(jié)等一系列問題,嚴重影響了機組運行的經(jīng)濟性和安全性。百葉窗作為運行可調(diào)因子,研究其開度對間接空冷散熱器的影響有利于對空冷塔的換熱狀況進行實時監(jiān)控,及時指導現(xiàn)場工作人員對其開度進行調(diào)控,尤其是出現(xiàn)散熱器受凍危險的情況。
Gu H F等[2]對1 000 MW機組的空冷塔采用百葉窗等4種措施進行了大風條件下提高自然通風塔的散熱性能研究。Yan W M等[3]通過實驗分析了空冷塔3種翅片管束換熱器的空氣流動特性和傳熱規(guī)律,得到了對流傳熱系數(shù)、壓降與進口風速的關(guān)系。周二奇[4]在利用數(shù)值模擬對某660 MW機組四塔合一式空冷塔傳熱性能研究中,研究了百葉窗開度等4個因素對四塔合一式空冷塔散熱性能的影響。盛波[5]在研究側(cè)風對間接空冷塔性能影響的數(shù)值研究及防風措施的探索中,研究了迎風面百葉窗開度調(diào)整等3種防風措施。殷明等[6]建立了百葉窗三維CFD(計算流體動力學)模型,并結(jié)合近似模型給出百葉窗結(jié)構(gòu)優(yōu)化方法,通過試驗設計以及CFD計算分析,得到空氣流經(jīng)百葉窗后的壓降。邢春禮等[7]采用實驗方法研究了結(jié)構(gòu)參數(shù)對濃縮器阻力損失的影響,結(jié)果表明,隨著百葉窗濃縮柵個數(shù)、間距及濃縮柵傾角的增加,百葉窗濃縮器的阻力損失減小。
綜上可見,對百葉窗以及其開度對間接空冷散熱器的影響的研究分析較少,且主要依據(jù)現(xiàn)場操作經(jīng)驗,缺乏必要理論依據(jù)。因此,筆者將基于流場仿真軟件CFX對SCAL型間接空冷散熱器的橢圓翅片管進行數(shù)值模擬,再結(jié)合4個不同百葉窗角度下的百葉窗風口數(shù)值模擬結(jié)果,分別從橢圓翅片管的傳熱規(guī)律和流動特性兩個方面進行深入分析,探究百葉窗開度對間接空冷散熱器的影響。
1 間接空冷散熱器翅片管計算模型
1.1 物理模型
以SCAL型間接空冷機組冷卻三角的散熱器管束為研究對象,每組管束包含多根串并聯(lián)翅片管,每根管由基管和翅片組成,采用雙排管雙流程的布置方式(見圖1)。基管為鋼制橢圓管,翅片為鋼翅片嵌套在橢圓基管上,橢圓基管及翅片外表面進行整體熱鍍鋅處理。翅片管道內(nèi)為熱介質(zhì)水,管外為冷介質(zhì)空氣,管內(nèi)循環(huán)冷卻水流經(jīng)橢圓單管與外界冷空氣進行熱量交換[8-10]。

圖1 散熱器翅片管模型
圖2為該翅片管束俯視結(jié)構(gòu)示意圖,表1為翅片管具體結(jié)構(gòu)參數(shù)。由于沿管長方向具有重復性的翅片結(jié)構(gòu)和相等的翅片間距,數(shù)值模擬建模時只考慮一個翅片。在橫向管間距方向,考慮翅片管的對稱性,通常取半個翅片(見圖2中虛線部分)。物理模型將整個計算域劃分為入口段、中間翅片管段(簡稱中間段)和出口段3部分。
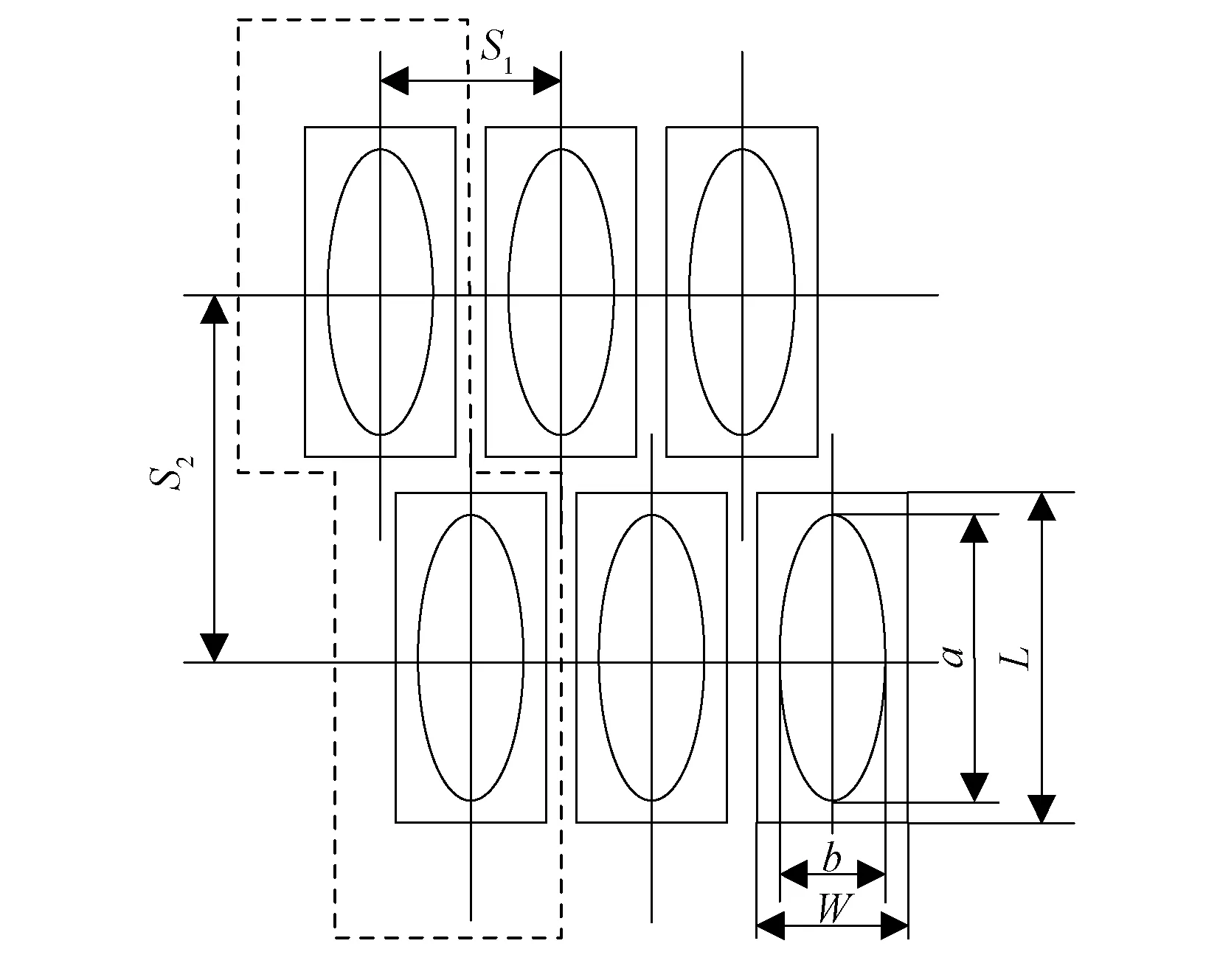
圖2 橢圓管翅片結(jié)構(gòu)俯視圖

項目數(shù)值基管尺寸(a×b×δ)1)/(mm×mm×mm)36×14×1.5翅片尺寸(L×W×m)2)/(mm×mm×mm)55×26×0.3翅片間距/mm2.5橫向間距S1/mm27縱向間距S2/mm61管排數(shù)2注:1)δ為基管壁厚;2)m為翅片厚度
圖3為翅片管束的計算物理模型。為了保證物理模型的可靠性及計算的穩(wěn)定性,建模時考慮了空氣入口區(qū)域和出口區(qū)域兩個延伸的區(qū)域:將進口區(qū)延長至2倍管徑的長度,目的是為了使空氣來流分布均勻,減小氣流不均勻性的影響,避免入口處的入口效應;出口延長至7倍管徑的長度,該區(qū)域的設定是為了減小空氣回流對模擬計算結(jié)果精度和準確性的影響[11]。

圖3 翅片管計算域
1.2 網(wǎng)格劃分
使用前處理軟件ICEM CFD 14.5進行網(wǎng)格劃分,分別對空氣流體域與翅片管實體域劃分網(wǎng)格。計算域的入口段、中間段和出口段分別生成網(wǎng)格,在管壁面及翅片表面附近網(wǎng)格較為密集;遠離壁面及翅片面的流體區(qū)域則采用較為稀疏的網(wǎng)格,達到節(jié)省計算時間、保證計算精度的目的。翅片管實體域網(wǎng)格特征見圖4,在翅片管壁處對網(wǎng)格適當加密,并通過ICEM檢驗網(wǎng)格質(zhì)量。同時,通過對翅片段網(wǎng)格不斷加密,檢驗計算結(jié)果的網(wǎng)格無關(guān)性,確保計算結(jié)果不受網(wǎng)格質(zhì)量和疏密程度的影響。最終翅片管束模型采用的空氣流體域網(wǎng)格數(shù)為1 370 436,翅片管實體域網(wǎng)格數(shù)為479 214。
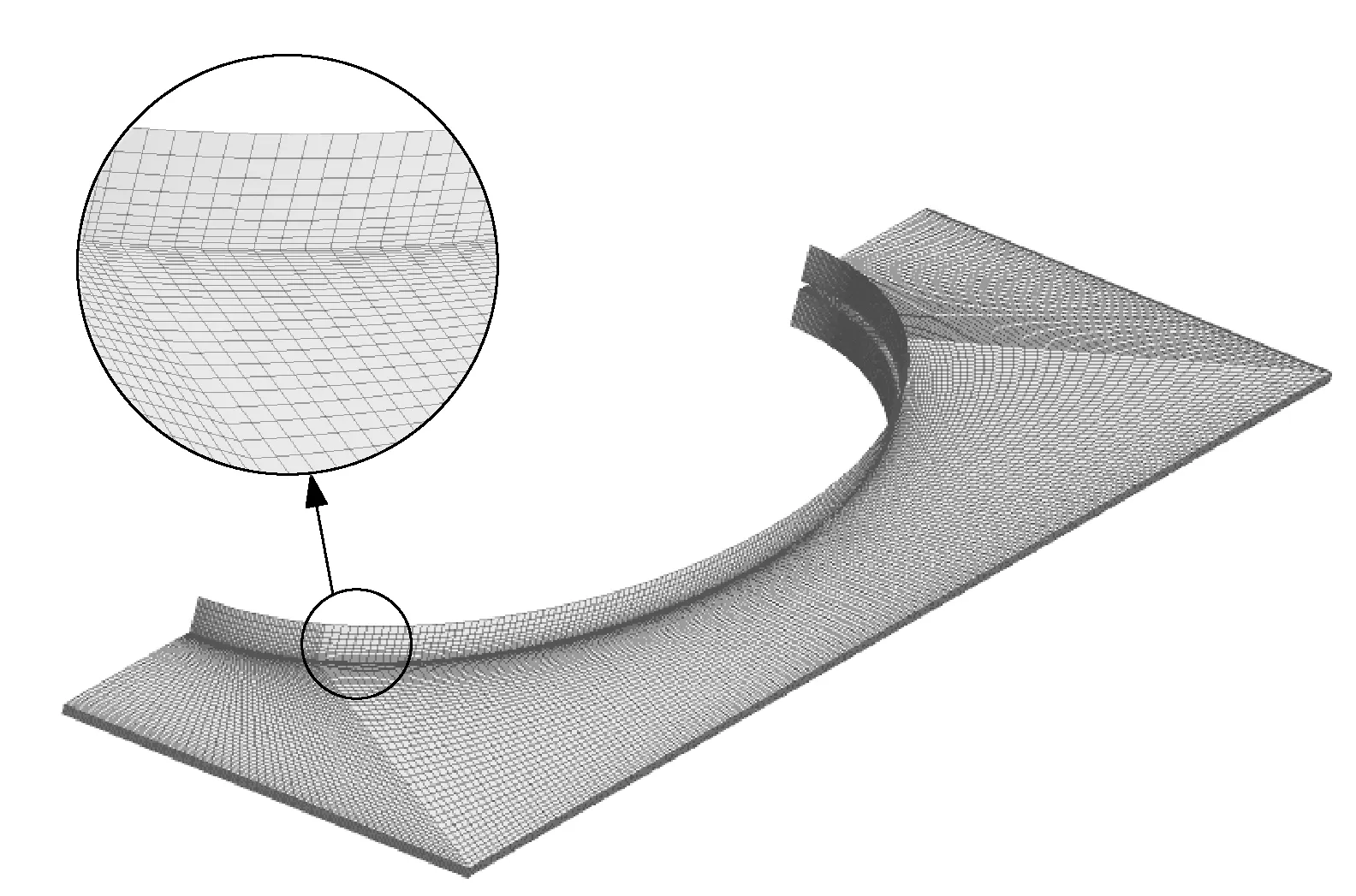
圖4 橢圓翅片管網(wǎng)格圖
1.3 基本假設及數(shù)學模型
計算域的入口段、中間段和出口段分別生成網(wǎng)格,在管壁面及翅片表面為方便建模及計算,對翅片管換熱元件作如下基本假設:
(1) 忽略輻射換熱、管內(nèi)外表面污垢熱阻及基管和翅片間的接觸熱阻。
(2) 管內(nèi)熱水流動為穩(wěn)定流動,管壁設為定壁溫。
(3) 計算域內(nèi)空氣的流動換熱為穩(wěn)態(tài),且流體在固體壁面無滑移。
(4) 不考慮空氣密度變化對流動換熱的影響,翅片的導熱系數(shù)為常量,即不考慮物性參數(shù)對流動換熱的影響。
采用Simple[12]算法求解N-S方程,由于翅片管束結(jié)構(gòu)復雜,空氣流經(jīng)翅片管束為紊流流動形式,采用標準k-ε模型描述[13],橢圓翅片管和空氣間的耦合換熱必須滿足連續(xù)性方程、動量守恒方程、能量守恒方程和控制方程。
1.4 邊界條件和其他輸入條件
1.4.1 空氣流體域
定義材料為25 ℃的空氣,忽略溫度變化導致空氣導熱系數(shù)的差異。入口設為速度入口,空氣速度變化在1~8 m/s,等距均勻插入8組工況。環(huán)境溫度變化在-30~16 ℃,取-30 ℃、-25 ℃、-20 ℃、-15 ℃、-10 ℃、-5 ℃、0 ℃、4 ℃、8 ℃、12 ℃、16 ℃共11組工況。出口設為標準大氣壓。
1.4.2 翅片管實體域
定義材料為鋼,管壁溫度設為37.7 ℃;考慮沿翅片厚度方向的導熱。
1.4.3 流固耦合面
建立空氣流體域和橢圓翅片管實體域的流固耦合面。設置空氣域耦合面為無滑移非光滑的壁面邊界條件。熱流密度q、溫度T應保持守恒,即滿足下列守恒方程:
(1)
式中:qf、qs為空氣流體域和翅片管實體域的熱流密度,J/(m2·s);Tf、Ts為空氣流體域和翅片管實體域耦合處的溫度, ℃。
1.4.4 周期性邊界條件和對稱邊界條件
沿管長方向的兩個面以及橢圓翅片管縱向截面方向都設為周期性邊界條件(見圖3)。
1.5 求解設置
CFX求解器中,Advection Scheme選擇為High Resolution模式,Turbulence Numerics選為一階。當計算殘差達到1.0×10-5,且流場中監(jiān)測點對應參數(shù)變化小于3%時,認定計算收斂。
1.6 模型驗證
為驗證數(shù)值模擬的準確性,對文獻[14]中類似問題的四排Forgo型管束進行了數(shù)值模擬,對比結(jié)果見圖5。計算結(jié)果表明:空氣側(cè)對流傳熱系數(shù)的平均誤差為2.61%,在可接受范圍內(nèi)。因此,計算結(jié)果與風洞試驗測出的傳熱系數(shù)較為吻合,說明計算采用的湍流模型可靠。

圖5 數(shù)值模擬與試驗結(jié)果對比圖
2 百葉窗模型
2.1 計算域
空氣進入百葉窗后,速度方向發(fā)生改變。在百葉窗風口中,對通風量產(chǎn)生影響的決定性因素為百葉窗角度,因此筆者研究百葉窗角度為30°、45°、60°、75°的情況。百葉窗的結(jié)構(gòu)見圖6。由于百葉窗在垂直于地面的方向(z軸)重復性的葉片結(jié)構(gòu)且等葉片間距,因此幾何建模只需考慮一個葉片,物理模型將整個計算域劃分為入口段、中間百葉窗葉片和出口段3部分,由于百葉窗葉片的厚度為2 mm,相對空冷塔冷卻三角的百葉窗整體高度13 m幾乎可以忽略不計,因此不考慮葉片厚度,視為一個無限薄面。不同的百葉窗角度θ對應著不同的百葉窗開度k,θ為0°對應百葉窗全開,θ為90°對應全關(guān),兩者對應關(guān)系為:
(2)

圖6 百葉窗結(jié)構(gòu)
2.2 邊界條件和其他輸入條件
(1) 入口條件設為速度入口,空氣速度變化在1~8 m/s,等距均勻插入8組工況。
(2) 出口條件設為壓力出口,設為標準大氣壓。
(3) 沿垂直地面方向(z軸)的兩個面設為周期性邊界條件(見圖3)。
(4) 壁面溫度設為37.7 ℃,環(huán)境溫度取-30~16 ℃,共10組來研究環(huán)境溫度的影響。
2.3 數(shù)值模擬過程
首先在ICEM中對物理模型劃分網(wǎng)格,并檢測網(wǎng)格無關(guān)性,然后利用基于有限容積法的商用軟件CFX對該模型進行求解,當計算殘差達到1.0×10-5,且流場中監(jiān)測點對應參數(shù)變化小于3%時,認定計算收斂。
2.4 模擬結(jié)果分析
2.4.1 流動阻力系數(shù)的計算
空氣流經(jīng)百葉窗的壓降通過CFX數(shù)值模擬得到:
Δp=pin-pout
(3)
式中:pin為空氣入口靜壓,Pa;pout為出口靜壓,Pa,邊界條件設該值為0。
進而可以得到百葉窗風口的阻力系數(shù):
(4)
式中:ρ為空氣密度,kg/m3;va為進口風速,m/s。由于此處為理論分析,因此不需考慮在工程應用時阻力系數(shù)的修正[15]。
部分工況的結(jié)果見表2。

表2 部分工況計算結(jié)果
2.4.2 阻力系數(shù)的影響因素
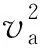
圖7為阻力系數(shù)隨進口風速的變化情況,可以看出:隨著進口風速的增大,ξ不斷增大且逐漸趨于平坦,空氣的湍流流動逐漸到達平方阻力區(qū),此時ξ不再隨進口風速的變化而變化。
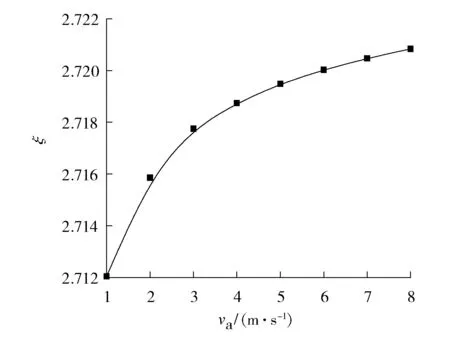
圖7 進口風速對百葉窗風口阻力系數(shù)的影響
圖8為進口風速為2 m/s時,不同百葉窗開度對百葉窗風口阻力系數(shù)的影響。

圖8 百葉窗角度對百葉窗阻力系數(shù)的影響
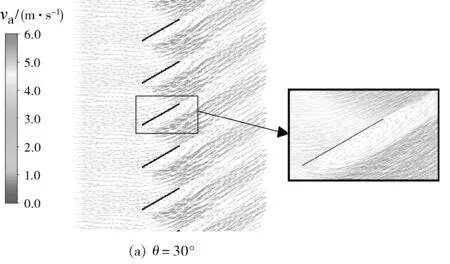
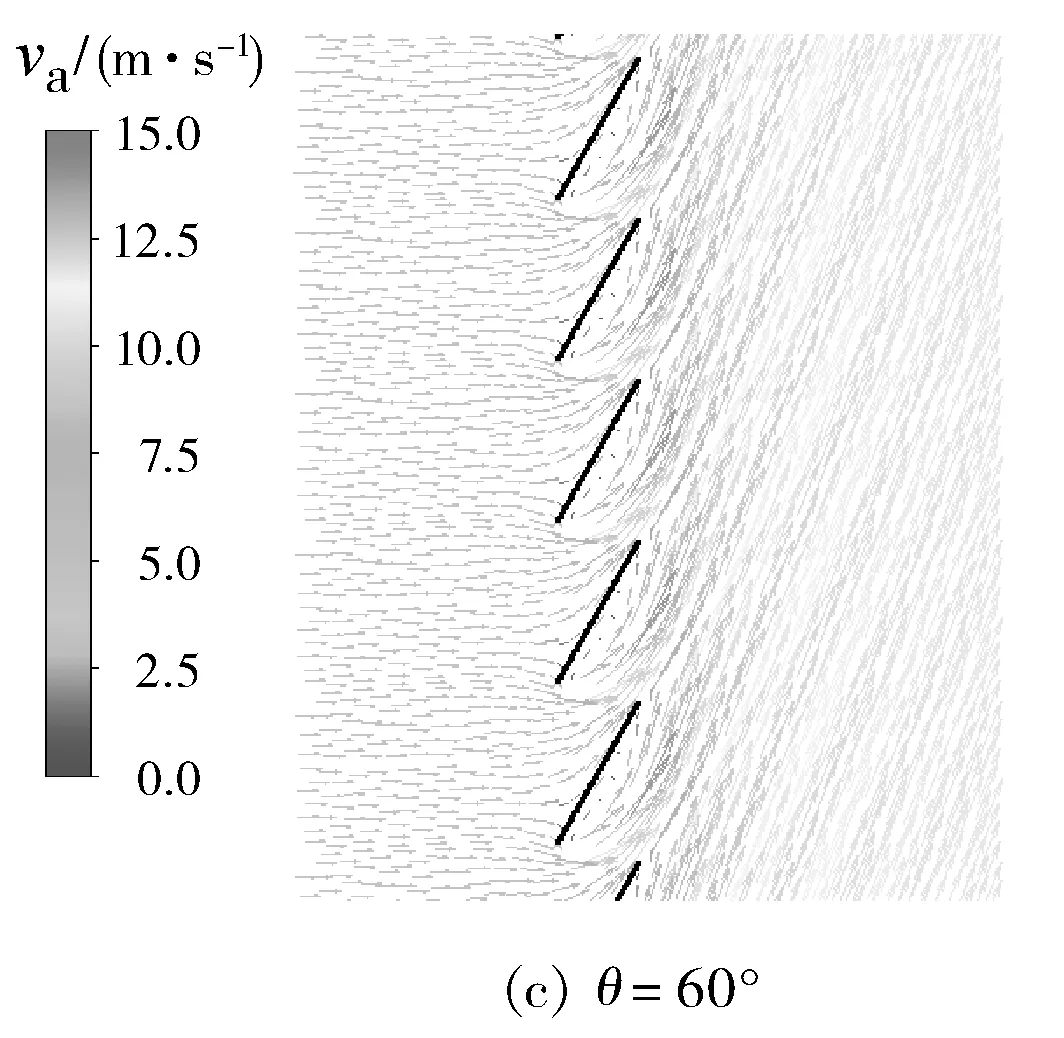
圖9為進口風速為2 m/s時,不同百葉窗開度下空氣經(jīng)過百葉窗葉片的流動特性對比圖。
分析圖8、圖9得出:百葉窗的開度越小則阻力損失越小。阻擋來流的葉片后面存在漩渦,漩渦區(qū)是負壓和低速區(qū),百葉窗葉片開度越大,其后面形成的漩渦區(qū)域越大,導致葉片前后的壓差較大,帶來較大的百葉窗風口阻力損失。當百葉窗開度為0°時即全開時幾乎不產(chǎn)生阻擋作用,因此阻力系數(shù)為0。
3 百葉窗開度對空冷散熱器的影響
3.1 速度入口條件的轉(zhuǎn)換計算
圖10為冷卻三角頂視圖,2片管束夾角約48°,垂直布置在支撐框架內(nèi)部,2片管束的缺口處安裝百葉窗。

圖10 冷卻三角頂視圖
通過第2節(jié)對百葉窗的數(shù)值模擬,可以得到空氣流經(jīng)百葉風口后的速度u和w,則進入間接空冷散熱器翅片管模型的入口條件計算公式為:

(5)
式中:u′、v′、w′分別為進入散熱器翅片管x、y、z三個方向的分速度。
3.2 計算結(jié)果
表3給出了部分工況計算結(jié)果[17],其中,ho為空氣與翅片管束的整體傳熱系數(shù),h1為經(jīng)過第一排管道的傳熱系數(shù),h2為第二排管束的傳熱系數(shù)。為區(qū)分空氣通過百葉窗風口和翅片管的壓降,分別用Δp1和Δp2來表示。

表3 部分工況計算結(jié)果
3.3 模擬結(jié)果及分析
3.3.1 流動特性分析
圖11為環(huán)境溫度為0 ℃時,不同的百葉窗角度、進口風速對總壓降的影響。從圖11可以看出:不同百葉窗角度下,空氣流動的總壓降均隨進口風速的增大而增大,同時,百葉窗的開度越大,空氣流經(jīng)百葉窗后再與翅片管進行換熱整個過程所造成的阻力損失越大。由第2.4節(jié)分析可知,這一阻力損失主要是百葉風口起到類似于擋板的作用。
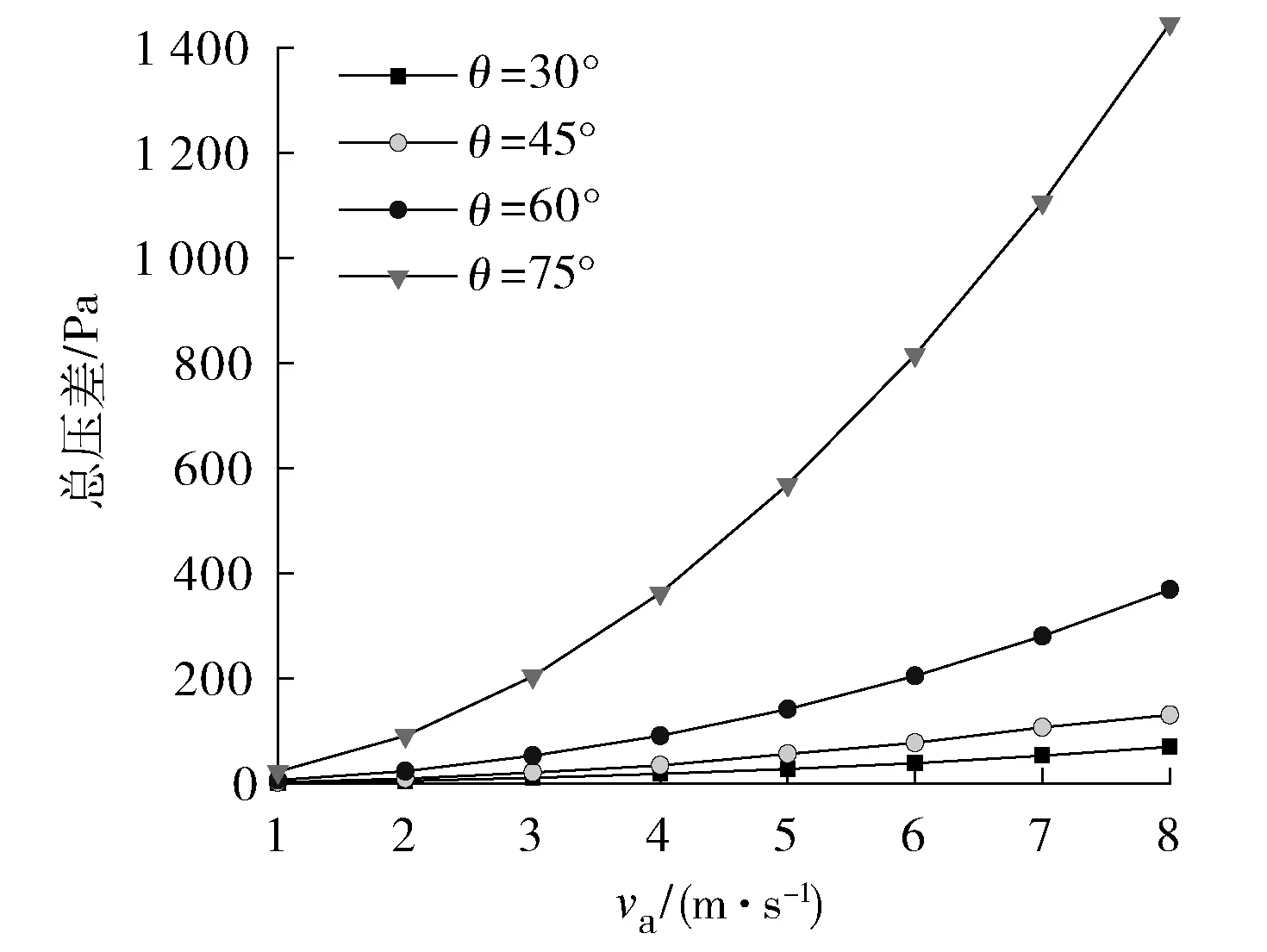
圖11 不同百葉窗角度下進口風速對總壓降的影響
圖12為環(huán)境溫度為0 ℃、百葉窗角度為45°、進口風速為4 m/s時,空氣流動截面(取軸向上表面周期性邊界條件截面:z=0.002 5 m)的壓力分布情況。
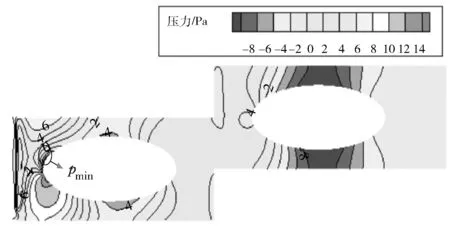
圖12 空氣流動截面壓力分布云圖
由圖12可見:空氣經(jīng)過翅片的壓差明顯降低,圖中標出位置為第一排管壓力的極小值pmin,可以看出壓力分布的等壓線不再關(guān)于橢圓長軸軸對稱分布,這是由于百葉窗的節(jié)流作用以及百葉窗與散熱器之間存在夾角。
3.3.2 傳熱規(guī)律分析
圖13為環(huán)境溫度為0 ℃,百葉窗角度為30°、45°、60°、75°時,空氣進入百葉窗與經(jīng)過橢圓管散熱器前后總壓差與翅片管平均對流傳熱系數(shù)之間的關(guān)系。
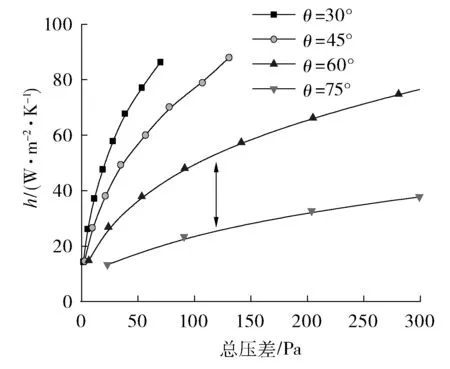
圖13 進出口壓差對傳熱系數(shù)的影響
分析圖13可以得出以下幾點結(jié)論:
(1) 空氣流經(jīng)進出口的壓差越大,與橢圓翅片管的傳熱系數(shù)就越大,且當壓差增大到一定程度時,橢圓翅片管的傳熱系數(shù)增加趨于平緩。
(2) 隨著百葉窗角度的逐漸增大,即開度逐漸減小,在一定的進出口壓差下,百葉窗的開度越小,dh/dθ變化越大。所以,在冬季百葉窗開度已經(jīng)很小時,對百葉窗進行調(diào)整時需要慎重,因為此時即使很小的開度變化也會引起橢圓翅片管束的傳熱系數(shù)很大的波動。因此,在冬季百葉窗本身已經(jīng)關(guān)得很小的情況下,對它的調(diào)節(jié)控制也就提出了更高的要求。
圖14為環(huán)境溫度為12 ℃、百葉窗角度為45°、進口風速為4 m/s時,空氣流動截面(取軸向上表面周期性邊界條件截面:z=0.002 5 m)的溫度分布。圖14中左側(cè)為第一排翅片,右側(cè)為第二排翅片。從圖14中看出:空氣經(jīng)過百葉窗的導向與節(jié)流作用在于翅片管發(fā)生換熱,進口處的速度方向發(fā)生了改變,在橢圓管束后形成的尾渦大小與形狀也發(fā)生了一定的改變,因此對管束的傳熱系數(shù)造成較大的影響。
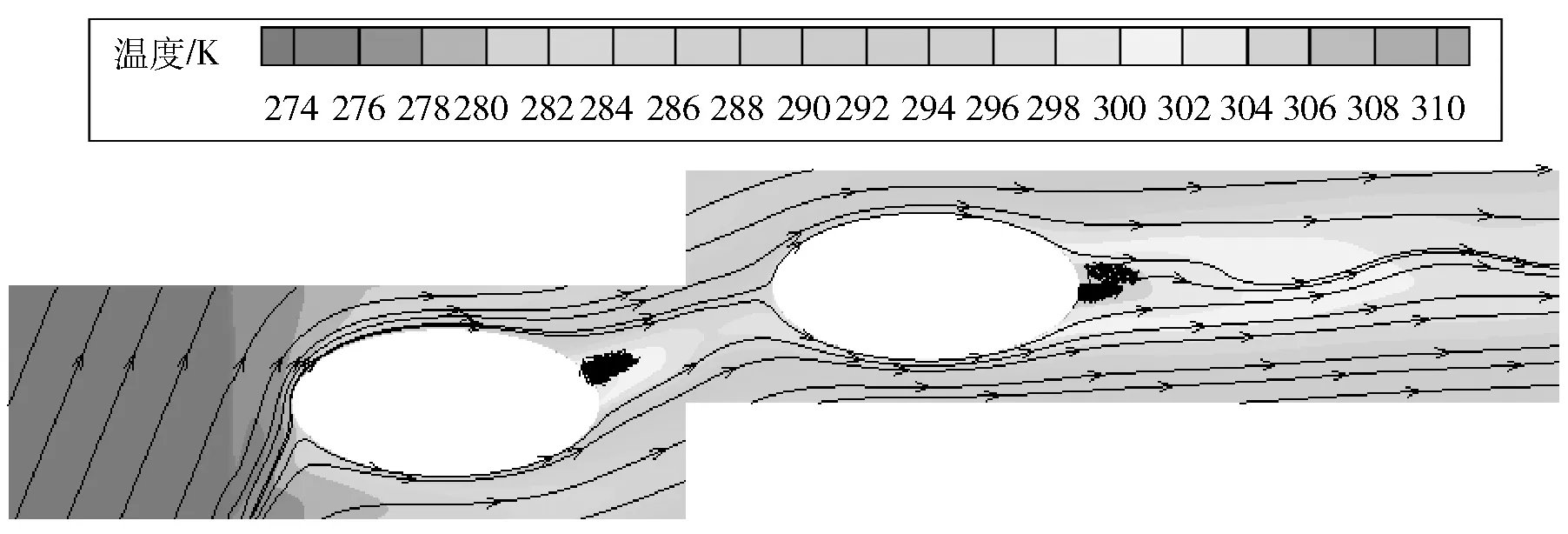
圖14 空氣流動截面溫度分布云圖
圖15為環(huán)境溫度為0 ℃、百葉窗角度為45°、進口風速為4 m/s時,流固耦合面(取橢圓翅片管翅片上截面:z=0.000 15 m)的溫度分布等溫線云圖,同樣等溫線最密集處出現(xiàn)了一定的偏移,原因同樣是百葉窗的導流與百葉窗與散熱器之間存在夾角的協(xié)同作用。

圖15 流固耦合面溫度分布云圖
4 結(jié)語
筆者利用CFX軟件對間接空冷翅片管和百葉窗風口進行了數(shù)值模擬,分析不同百葉窗角度下空氣的流動特性,為下一步研究做好準備。研究百葉窗開度對翅片管換熱的影響,即將空氣經(jīng)過百葉窗模型后的出口條件作為橢圓翅片管模型的入口條件,從而將兩者結(jié)合起來分析。具體結(jié)論如下:
(1) 百葉窗的開度越大,空氣流經(jīng)百葉窗后再與翅片管進行換熱整個過程所造成的阻力損失越大。
(2) 由于百葉窗的導流作用以及百葉窗與散熱器之間夾角的存在,空氣經(jīng)過翅片的壓差明顯降低,且壓力分布的等壓線不關(guān)于橢圓長軸軸對稱分布。
(3) 隨著百葉窗角度的逐漸增大,即開度逐漸減小,在一定的進出口壓差下,百葉窗的開度越小,dh/dθ變化越大。冬季百葉窗開度已經(jīng)很小時,對百葉窗進行調(diào)整時需要慎重。
(4) 由于百葉窗的導流作用及其與散熱器之間夾角的協(xié)同作用,使得翅片管空氣流動截面的溫度分布以及流固耦合面溫度分布出現(xiàn)了一定的位置偏移。

