基于Bonferroni均值算子的跨境電商發展水平直覺模糊評價方法

周金明

(安徽工程大學 數理學院，安徽 蕪湖 241000)

跨境貿易電子商務作為一種具有前瞻性的新型跨境貿易模式，引領著全球電子商務的發展潮流.中國跨境電子商務行業仍處于初級發展階段，投資、融資事件如雨后春筍，整體行業資產快速增長.截止到2015年8月初，全國共有9個跨境電商進口試點城市為寧波、鄭州、上海、重慶、杭州、廣州、深圳、福州、平潭；全國跨境貿易電子商務服務試點城市包括鄭州、杭州、重慶、上海、寧波、廣州、深圳、天津共8個城市.2015年，出口跨境電商紛紛轉型進口，大量傳統外貿開始觸及跨境電商；中國跨境電子商務市場規模將達5.3萬億元，同比增長32%;中國跨境電子商務行業交易額占進出口貿易總額19.4%.

針對跨境電商行業發展水平進行評價，可以把握各區域的發展均衡狀態，反映電商行業發展趨勢和機遇，反映跨境電商的特色和潛在優勢等.文獻[1]應用“技術—組織—環境”三維框架的思想和要素模型分析方法，在運用擴展關系數據庫描述方式的基礎上，對跨境電子商務的跨境主體、跨境環境、配套服務三維模型進行了擴展,對我國主要城市跨境電子商務發展水平進行了定量評價和層級劃分.楊堅爭[2]等通過因子分析法研究得出5個對跨境電子商務發展有重要影響的指標，并應用指標體系對我國各地的跨境電子商務發展狀況進行了研究分析.

縱觀跨境電子商務發展水平評價的研究，考慮跨境電子商務評價指標的模糊性和不確定性的文獻尚不多見.在評價活動中，由于指標之間還存在一定的相互關系，同時要兼顧評價過程科學性原則、可操作性原則與公平原則[3].鑒于此，提出基于加權直覺模糊Bonferroni調和均值算子(WIFBHM)的決策方法，并對某省份跨境電商部分區域發展水平進行測度與評價.

1 Bonferroni算子相關概念

1.1 Bonferroni均值的定義與性質

Bonferroni均值(Bonferroni Mean,簡記為BM)算子[3]可以將多個輸入變量集結為一個輸出變量，是一種介于最大和最小之間的集成算子，它主要的優點是在集成過程中可以反映每一個輸入變量與其他輸入變量之間的相互關系.

定義1[4]設p,q≥0,ai(i=1,2,…,n)是非負實數集.若

(1)

稱其為Bonferroni均值，易知該均值有如下性質：

(1)BMp,q(0,0,…,0)=0.

(2)(冪等性)BMp,q(a,a,…,a)=a.

(3)(單調性)BMp,q(a1,a2,…,an)≥BMp,q(b1,b2,…,bn),即BMp,q是單調的如果ai≥bi,(i=1,2,…,n).

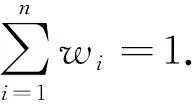
(2)

稱其為加權Bonferroni均值(Weighted Bonferroni Mean，WBM).

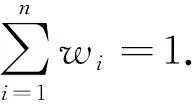
(3)

稱其為加權Bonferroni調和均值(Weighted Bonferroni Harmonic Mean,WBHM)，WBHM同樣具有優良性質即冪等性、單調性、可交換性和有界性.

1.2 梯形直覺模糊數的定義與代數運算

自Atanassov提出直覺模糊集(Intuitionistic Fuzzy Set,IFS)以來，因IFS綜合考慮了隸屬度、非隸屬度和猶豫度三方面的信息，從而能更加細膩地描述和刻畫客觀世界的模糊性本質，眾多學者對IFS進行了深入研究[6-9].模糊數表示不確定的量化問題有明顯優勢，而作為模糊數的推廣即直覺模糊數可以更好地表示模糊的內涵.文獻[10]給出了三角直覺模糊數的定義.

定義4 集合A為含參變量a1,a,b,c,d,d1的梯形直覺模糊數(Trapezoidal Intuitionistic Fuzzy Number，TrIFN)為實數集R上的集合，記作A={([a,b,c,d];ωA),([a1,b,c,d1];uA)}，其隸屬度和非隸屬度定義如下：

(4)

(5)

式中,ωA,uA分別表示隸屬度的最大度和非隸屬度的最小度，且滿足條件:

0≤ωA≤1,0≤uA≤1,0≤ωA+uA≤1.

設πA(x)為表示x屬于A的猶豫度,且πA(x)=1-μA(x)-vA(x).為了討論的簡潔性，取[a,b,c,d]=[a1,b,c,d1],則TrIFNA表示為A=([a,b,c,d];ω1,uA).當b=c時,TrIFN退化為三角直覺模糊數.

定義5[11]設A1=([a1,b1,c1,d1];ωA1,uA1),A2=([a2,b2,c2,d2];ωA2,uA2)為TrIFNs,λ>0,TrIFN的運算定義如下:

(1)A1⊕A2=([a1+a2,b1+b2,c1+c2,d1+d2];ωA1∧ωA2,uA1∨uA2),其中“∧”“∨”分別表示取大取小算子;

(2)A1?A2=([a1a2,b1b2,c1c2,d1d2];ωA1∧ωA2,uA1∨uA2);

(3)λA1=([λa1,λb1,λc1,λd1];ωA1,uA1);

定義6[12]TrIFNA=([a,b,c,d];ωA,uA)的α-割集定義為A(α)={x|μA(x)≥α},0≤α≤ωA.

由式(4)和定義6,α-割集是一個閉區間記作A(α)=[AL(α),AU(α)],

(6)

定義7[12]TrIFNA=([a,b,c,d];ωA,uA)的β-割集定義為A(β)={x|μA(x)≤β},0≤uA≤β≤1.

由式(5)和定義7,β-割集也是一個閉區間記作A(β)=[AL(β),AU(β)],

(7)

2 梯形直覺模糊數的排序

利用(α,β)-割集進行梯形模糊數的排序.文獻[13]給出了區間數的排序問題，設a=[aL,aU],b=[bL,bU]為任意給定的區間數，且aL≤aU,bL≤bU.若aL=aU,則區間數退化為一個實數a′,即a′=aL=aU.

定義8 設a,b為任意實數,則a>b的可能度定義為:

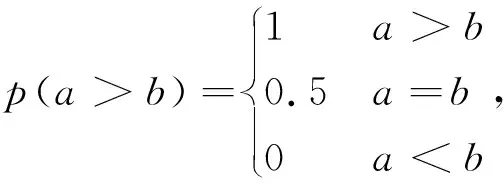
(8)

定義9 設a=[aL,aU],a=[bL,bU]為任意實數,則a≥b的可能度定義如下為:

(9)

3 加權梯形直覺模糊Bonferroni調和均值算子

由TrIFBHM的加權形式，提出基于加權TrIFBHM的綜合評價問題.

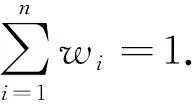
(10)

稱WTrIFBHMp，q為加權梯形直覺模糊數Bonferroni調和均值(Weighted Trapezoidal Intuitionistic Fuzzy Bonferroni Harmonic Mean),由梯形模糊數運算律式(1)～式(4),可得定理1.

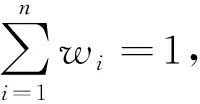
WTrIFBHMp,q(A1,A2,…,An)=

(11)

由WTrIFBHM的定義易知，WTrIFBHM具有冪等性、可交換性和單調性：

性質1(冪等性)若Ai(i=1,2,…,n)均相等,即Ai=A=([a,b,c,d],ωA,uA),則

WTrIFBHMp,q(A1,A2,…,An)=WTrIFBHMp,q(A,A,…,A)=A.

(12)

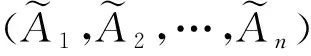
(13)

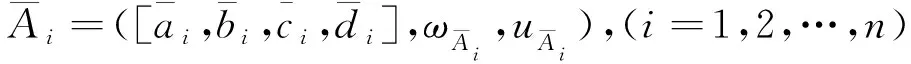
(14)

由性質1與性質3易知，WTrIFBHM具備有界性即性質4：

性質4(有界性)設Ai=([ai,bi,ci,di],ωAi,uAi),(i=1,2,…,n)為TrIFNs集.記A-=([∧iai,∧ibi,∧ici,∧idi],∧iωAi,∨iuAi),A+=([∨iai,∨ibi,∨ici,∨idi],∨iωAi,∧iuAi),則

A-≤WTrIFBHMp,q(A1,A2,…,An)≤A+.

(15)

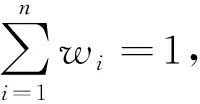
(16)

Aσ(i)=([aσ(i),bσ(i),cσ(i),dσ(i)],ωAσ(i),uAσ(i)),(i=1,2,…,n),(σ(1),σ(2),…,σ(n))是(1,2,…,n)的一個全排列,使得Aσ(i-1)≥Aσ(i),(1,2,…,n).

4 梯形直覺模糊信息下的多指標綜合評價

4.1 基于WTrIFBHM的綜合評價方法步驟

下面給出基于加權三角直覺模糊數的綜合評價問題，具體步驟如下：

步驟1:構造專家評價矩陣Dt.

步驟2:利用集成算子Ai=WTrIFBHMp,q(Ai1,Ai2,…,Aim),計算綜合評價值.

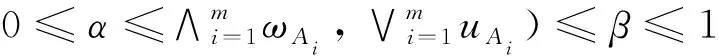
步驟4:計算Ai(λ)

(17)

其中，λ可以反映決策者關于隸屬度及非隸屬度的偏好水平(λ∈[0,1]).

步驟5:構造判斷矩陣P

P=(pij)m×m,

(18)

其中,由式(9)計算pij=p(Ai≥Aj)=p(Ai(λ)≥Aj(λ)),1≤i≤m,1≤j≤m.

步驟6:計算Ai(i=1,2,…,m)的排序指數RI(Ai)[13]

(19)

步驟7:根據RI(Ai)(i=1,2,…,m)對TrIFNsAi(i=1,2,…,m)進行排序.

4.2 應用實例

考慮對某省份甲、乙、丙、丁4個跨境電商部分區域發展水平進行評價，設評價對象集為O={o1,o2,o3,o4},o1,o2,o3,o4分別代表甲、乙、丙、丁4個區域.根據所構建的跨境電商區域發展水平評價指標體系構建屬性集C={C1,C2,C3,C4}：C1表示跨境電商物流發展水平；C2表示跨境電子支付發展水平；C3表示電子通關發展水平；C4表示跨境電商基礎設施與環境支持水平.其指標權重分別為w=(0.23,0.20,0.27,0.30)T(指標權重可以采用主客觀組合賦權法可得，算例中指標權重利用基于最小二乘的AHP-信息熵組合方法得到).現有4個跨境電商專家D={D1,D2,D3,D4}，專家權重分配為η=(0.25,0.25,0.25,0.25)T，4位專家對4個城市的電子商務發展水平進行評價，結果如表1～表4所示.利用研究提出的WTrIFBHM方法，對專家評價矩陣進行計算(Microsoft Windows 10操作系統和AMD A8-7100 Radeon R5，Core 4C+4 G 1.80 GHz 4.0 GB計算機環境下，利用Matlab R2012b實現)．

表1 專家D1給出的評價矩陣A(1)

表2 專家D2給出的評價矩陣A(2)

表3 專家D3給出的評價矩陣A(3)

表4 專家D4給出的評價矩陣A(4)

(1)首先輸入規范決策矩陣A(k)(k=1,2,3,4)與指標權重；

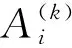
(3)利用專家權重向量η，計算得到綜合評價值如下：

A1=([0.18,0.28,0.37,0.50];0.5,0.5),A2=([0.22,0.30,0.37,0.45];0.5,0.4),

A3=([0.17,0.29,0.38,0.47];0.5,0.4),A4=([0.20,0.36,0.46,0.54];0.5,0.5).

(4)計算排序等級指數RI(Ai)(取α=β=λ=0.5)，

RI(A1)=0.191,RI(A2)=0.205,RI(A3)=0.199,RI(A4)=0.328.

即o1?o2?o3?o4.利用研究中方法的排序結果表明：區域丁屬于該省跨境電商發展的主力,區域乙次之，區域丙與區域甲的跨境電商發展尚處于起步階段.

5 結束語

針對跨境電子商務發展趨勢，提出了跨境電子商務發展的水平評價，并運用直覺模糊集處理評價的模糊性和不確定性，采用直覺模糊多屬性群決策方法對跨境電商區域發展水平進行評價.對某省份部分區域跨境電子商務的發展水平進行評價，評價結果對該省跨境電商發展有一定的參考價值.研究在BM算子的基礎上，提出了TrIFBHM，WTrIFBHM和WTrIFOBHM等算子，探討了各算子的優良性質.這些算子適用于處理準則和專家的權重系數均已知，專家給出的備選方案對決策準則的屬性權重為梯形模糊數的模糊多準則群決策問題.該方法的主要特點在于考慮了綜合評價指標間的關聯性，使評價結果更接近實際問題的情況，評價結果更加合理；可操作性強，該方法除了需要通過主客觀賦權方法對指標進行賦權,其他程序都可以通過計算機實現.在保證評價專家具有代表性的前提下，可應用于規模較大的企業或政府部門的業績評價等領域.

結合Bonferroni均值直覺模糊評價方法，采用多個評價主體參與評價，可以提高群組評價的準確性和有效性,是非常有意義的.如何通過對群組評價結果的系統記錄，增強組織者選擇評價專家的科學性，還有待于進一步研究.