波浪對非淹沒豎直圓柱作用的數值分析

吳 昊，朱際休，廖 斌，陳善群*

(1.安徽工程大學 建筑工程學院，安徽 蕪湖 241000；2.中冶建筑研究總院有限公司，北京 100088)

非淹沒豎直圓柱通常可見于近海風力發電機、海上導航燈塔、石油和天然氣平臺的支撐以及系泊結構.波浪與非淹沒豎直圓柱相互作用時，由于圓柱結構本身物理性質會改變入射波場的特性進而影響波浪衍射和反射的波動過程.對于兩串聯豎直圓柱而言，主要有直接作用在圓柱上的入射波；波浪由于圓柱分隔水作用形成的衍射波；波浪與圓柱作用形成的反射波；不同類別波之間復雜的相互作用.與此同時，波浪作用在豎直圓柱形式的海洋構筑物上會對結構產生沖擊作用繼而使得自由液面高程抬升，波浪的這些作用會對海洋構筑物的承載力和穩定性造成很大的影響.因此系統開展波浪與非淹沒豎直圓柱相互作用的研究，對于準確預測作用在非淹沒豎直圓柱上的波浪力和自由液面具有很大的工程意義.

近年來，國內外學者就波浪與圓柱作用開展了一系列工作，典型工作有武昕竹[1]等采用VOF模型對聚焦波與單個直立圓柱作用進行數值模擬，通過計算得到圓柱周圍波浪力和波浪波動過程與實驗結果吻合較好.唐鵬[2]等通過求解Navier-Stokes方程，VOF模型捕捉自由液面，在三維波浪數值水槽中對單個圓柱周圍波浪爬升效應進行計算，結果表明該數值模型可以較好地研究單個豎直圓柱爬升問題.蔣昌波[3]等在數值模擬中使用修正后的VOF模型對孤立波作用在單圓柱附近的流動特性進行研究，計算結果表明，圓柱附近自由液面沿柱面呈現三維分布并且觀察到孤立波上爬過程中圓柱迎風面水位壅高效果顯著大于回落過程.Morgan[4]等采用Open FOAM模擬了聚焦波浪對單個豎直圓柱進行作用，計算結果準確再現了圓柱附近的衍射波，并且通過計算得到作用在圓柱上的波浪力與實驗結果較為吻合.Mo[5]等對單個細長豎直圓柱的實驗結果進行測試，測試結果表明波浪與細長豎直圓柱作用時波浪不會破碎，湍流作用可以忽略不計，隨后在數值模擬過程中通過合理運用入射邊界條件更好地預測了自由液面高程、波浪水粒子速度等.

目前數值方法中大都采用VOF模型就波浪與單個非淹沒豎直圓柱相互作用的問題進行研究，對于波浪與多個非淹沒豎直圓柱相互作用涉及很少，而大部分海洋構筑物一般由兩個以上的圓柱構成.基于此，通過求解Navier-Stokes方程(RANS)，利用Level-set方法對自由液面進行追蹤，采用松弛方法實現造波和消波的過程，并建立三維數值水槽.通過數值模擬方法預測單個圓柱的波浪力、測點自由液面高程等物理量，參照Mo[5]等的實驗結果進行比較，驗證了數值模型的合理性與準確性.在此基礎上，主要研究了圓柱間距對兩串聯圓柱所受波浪力與自由液面高程的影響.

1 數值模型

數值模型基于不可壓縮的三維雷諾時均Navier-Stokes方程(RANS)，結合質量和動量守恒方程求解三維數值水槽中波浪傳播的問題，控制方程如下：

(1)

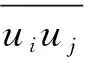
研究壓力項采用Chorin[6]提出的投影算法確定，由此產生的泊松方程用預處理BiCGStab[7]求解器進行求解；對流項采用Jiang[8]等提出的WENO5格式進行離散化求解；為了保證WENO5格式的精度和穩定性，采用Shu[9]等提出的三階龍格庫塔顯式時間格式(Third-order Runge-Kutta Theme)；為了避免數值水槽中由于波動引起湍流的非物理現象過度產生，在采用Wilcox[10]兩方程k-ω湍流模型封閉RANS方程的同時采用Durbin[11]渦流粘度限制器.

波浪與非淹沒式豎直圓柱相互作用通常伴隨著復雜的界面演化過程，最大的難點是對自由液面的追蹤.采用Osher[12]等提出的Level-Set方法進行求解，并且在每次迭代過程中都要采用Peng[13]等方法進行重新初始化，從而達到對自由液面波浪演化過程的精細刻畫.

2 波浪對單個非淹沒豎直圓柱作用的算例驗證

波浪作用在單個圓柱上的傳播示意圖如圖1所示.數值水槽中造波和消波采用松弛法[14]，松弛函數選取Jacobsen[15]，松弛法造波的實質是在造波區域和消波區域將自由液面、壓強、水平和垂直速度進行實時更新.波浪造波長度為L，為了避免壁面反射的波浪對數值結果產生影響，在水槽的尾端設置2L的消波區域，其中L為一個波長長度.圖1中D為豎直圓柱直徑；L為波浪生成的波長；h0表示靜水深度.三維數值水槽計算域x方向長132 m，y方向寬5 m，z方向高8 m；波高H=1.2 m；波浪周期T=4.0 s；初始靜止水深h0=4.76 m；圓柱直徑D=0.7 m，貫穿整個計算域；其中圓柱圓心距造波區前端65.9 m；KC數大小為6.1.為了探究波浪對單個非淹沒豎直圓柱周圍自由液面和波浪力的影響，在數值水槽的邊緣處布置測點P1，圓柱附近分別布置測點(P2、P3、P4).

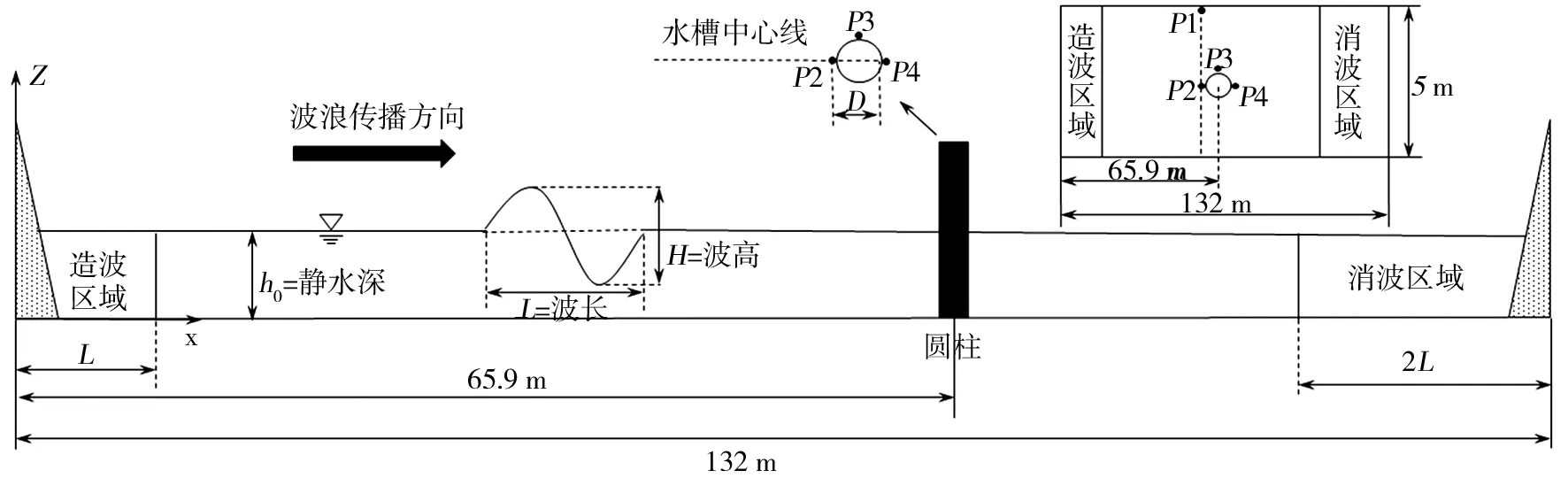
圖1 單個非淹沒豎直圓柱波浪傳播示意圖

網格的劃分和自由液面演化如圖2a和圖2b所示.其中三維數值水槽網格的設置采用四面體結構網格(Euler網格)，在保證各物理量計算結果穩定的情況下，同時兼顧節約計算資源，設置Δmin=0.1，網格單元總數為528萬單元；關于自適應時間步長，選取CFL=0.1的限制條件來保證計算結果的準確性.

圖2 三維數值水槽計算域示意圖

作用在單個非淹沒式豎直圓柱的波浪力驗證如圖3所示.P1及圓柱周圍(P2～P4)測點自由液面高程驗證如圖4所示.由圖3、圖4可知，將單個非淹沒豎直圓柱波浪力和各測點自由液面演化過程預測結果與Mo[5]等實驗結果進行對比，其中作用在豎直圓柱上的波浪力計算方法采用文獻[16]的方法，波浪力采用無量綱F′=F/ρgDH2，各測點自由液面高程采用無量綱η′=η/ηmax,p1，其中第一個波峰處的振幅被認為是靠近壁面測量的最大振幅ηmax,p1，t/T是無量綱周期；從圖3中可以看出數值模擬預測的結果與實驗結果吻合較好.圖4a數值模擬得到壁面附近(測點P1)的自由液面高程與實驗結果之間具有一致性，表明了數值水槽中的入射波和衍射波不會對壁面處的自由液面高程產生影響.以上證明了本研究數值模擬的方法具有較高的準確性和可靠性.

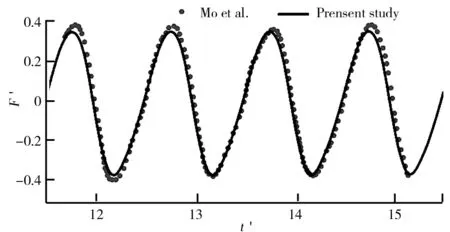
圖3 作用在單個非淹沒式豎直圓柱的波浪力驗證

3 波浪對兩串聯非淹沒豎直圓柱的作用

3.1 兩串聯非淹沒豎直圓柱波浪力

串聯兩個圓柱波浪傳播示意圖如圖5所示.由圖5可知，D為豎直圓柱直徑；L為生成波浪的波長；h0表示靜水深度；S為兩個圓柱之間的凈間距.三維數值水槽計算域x方向長15 m，y方向寬5 m，z方向高1 m；初始靜水深h0=0.5 m；圓柱直徑D=0.5 m，貫穿整個計算域，各物理量的無量綱參照前面所示.其中圓柱1中心距離造波區前端7 m.同時在上游圓柱1附近位置處布置3個測點(B1、B2、B3)來監控自由液面高程，波浪傳播示意圖如圖5所示.

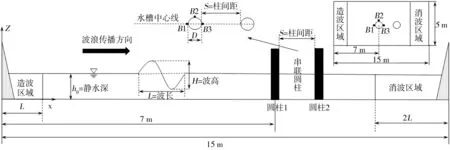
圖5 串聯兩個圓柱波浪傳播示意圖

為了探究圓柱間距S對兩串聯狀態中上游和下游圓柱附近自由液面高程η′和波浪力F′的影響，列出了單圓柱工況(T1)與兩串聯豎直圓柱工況(S1～S4)進行對比分析.其中5nd-Order Stokes波長L為2m，波陡H/L=0.1，波浪周期T=1.18 s，計算求得KC數為1.37，具體計算工況如表1所示.

表1 兩串聯圓柱計算工況

注：T1為波浪作用在單圓柱情況下

T1工況中單個圓柱附近測點的高程如圖6所示.測點分別布置在圓柱附近(B1、B2、B3)，具體布置形式如圖7所示.從圖7中可以看出，在T1工況中圓柱迎風面(測點B1)的自由液面高程η′大于背風面(B3)自由液面高程η′.根據Kamath[17]等關于用三維數值水槽對圓柱波浪力的研究可知，波浪在慣性主導力的作用下，隨著入射波到達圓柱附近，由于圓柱分隔水的作用，波浪在圓柱周圍產生衍射波并向四周發散造成圓柱迎風和背風區形成更大的靜壓力差，因此導致了測點高程(B1>B3).

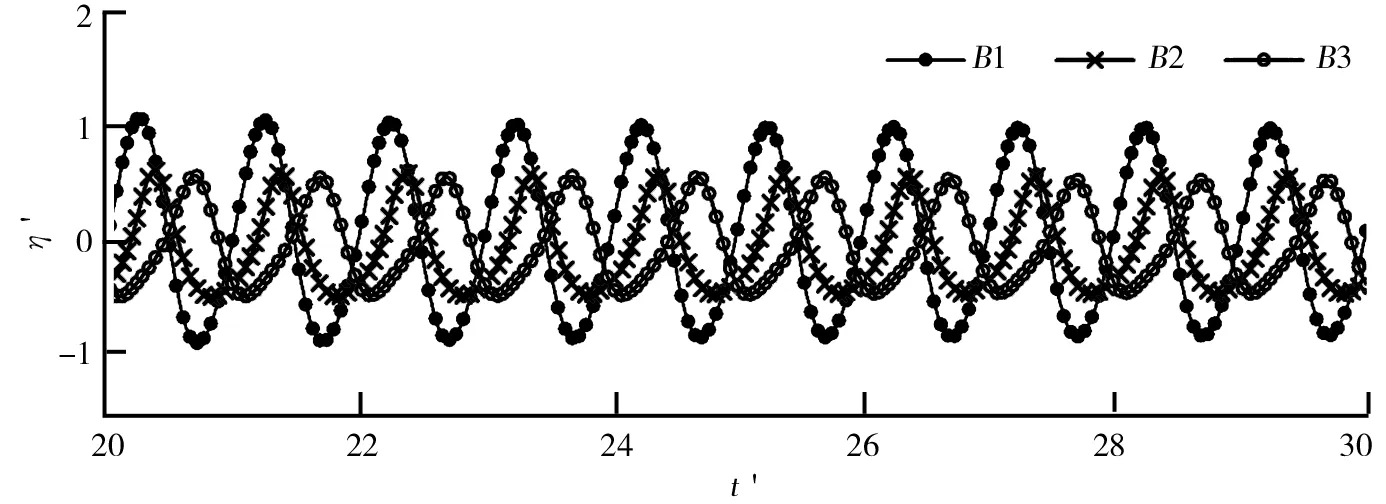
圖6 單個圓柱附近測點的高程

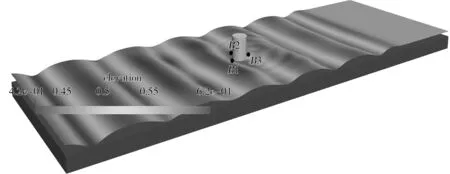
圖7 T1工況下單個圓柱附近測點的高程云圖

為探究圓柱間距S對兩串聯豎直圓柱波浪力的影響，主要分析了(S1～S4工況)中單個周期t′內波浪力F′的演化曲線，如圖8所示.圖8中單個圓柱的波浪力F′是在T1工況條件下產生的.從圖8a中可以看出，在S1工況中上游圓柱1較單個圓柱和下游圓柱2的波浪力F′有所提高；從圖8b～圖8d可以看出，隨著圓柱間距S的不斷增大，上游圓柱1和單個圓柱的波浪力F′差距不大，尤其在圖8d中，上游圓柱1與單圓柱的波浪力F′差距很小.這說明隨著圓柱間距S的增大，圓柱之間壅水效果越來越不明顯使得作用在圓柱上的波浪力F′也隨之降低.

在S1工況中(S=0.5D)，圓柱間距S相對其他工況(S2～S4工況)較小，圓柱之間壅水效果增強，導致了S1工況(見圖8a)中上游圓柱1的波浪力高于單個圓柱的波浪力；而工況為S2～S4的情況也即柱間距S=1D～4D時(見圖8b～圖8d)，由于圓柱間距S的增大，圓柱之間的壅水效果沒有S=0.5D明顯，在兩串聯圓柱工況中，上游圓柱1單周期t′內波浪力F′的演化曲線與單圓柱的波浪力F′演化曲線有貼合趨勢，只是相位上有少許差異，這一結論在圓柱間距S=4D中更為明顯.由此可知，圓柱間距在S=4D時來自下游圓柱2的壅水效果已經不是很明顯，因此在兩串聯豎直圓柱中，作用在上游圓柱1的波浪力與單個圓柱相似.波浪在不同圓柱間距S下產生的波浪力有著不同的差異，基于此就S1和S4工況(即S=0.5D，S=4D)研究自由液面的高程.

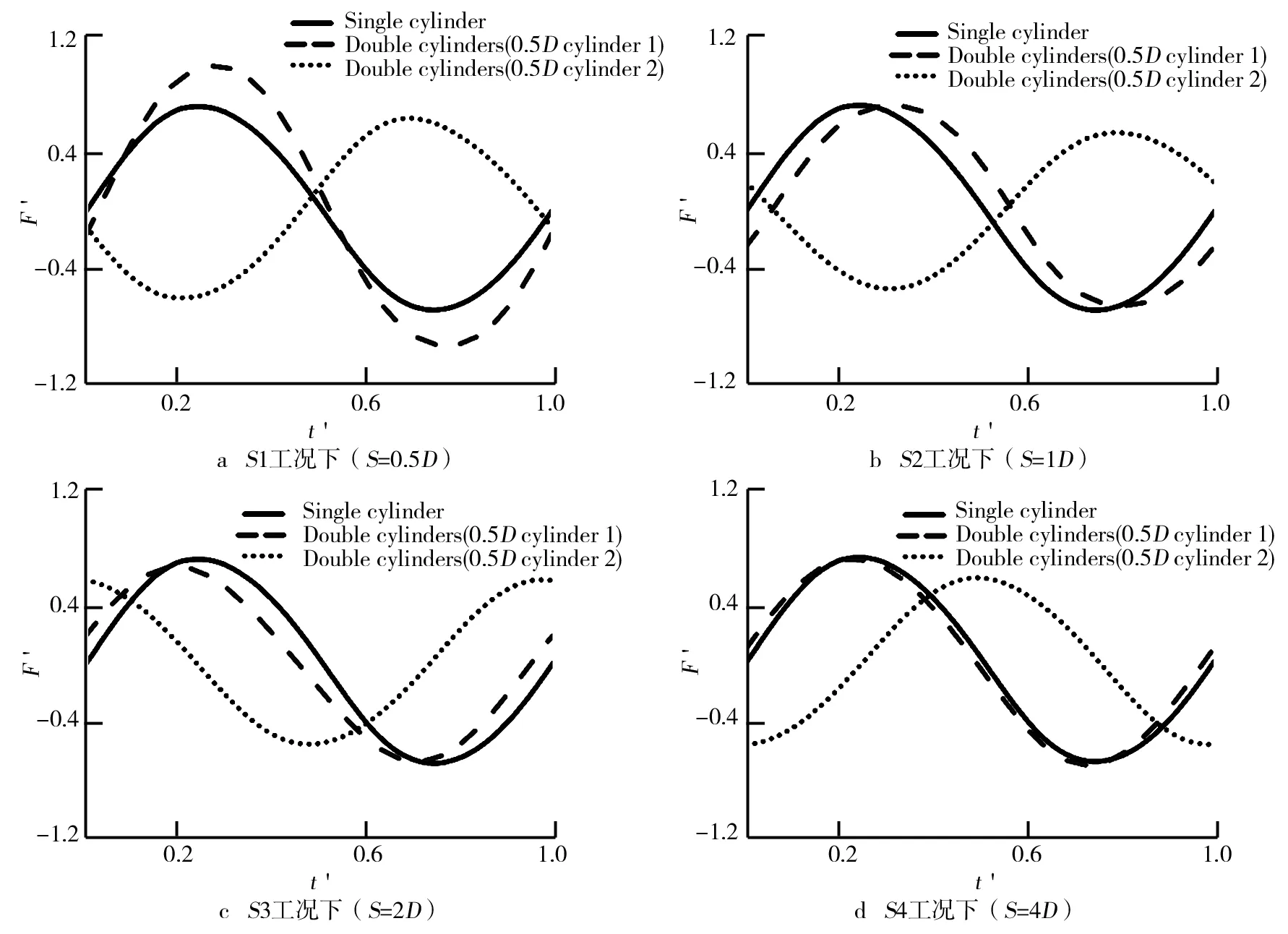
圖8 不同柱間距工況下單個周期t′內波浪力F′演化曲線

3.2 兩串聯非淹沒豎直圓柱自由液面高程

選取圓柱間距S=0.5D和S=4D工況下各測點單個周期t′內自由液面高程η′的演化曲線，如圖9所示.測點B1(圖9a)受入射波的直接作用，可以觀察到圓柱間距S=0.5D和S=4D的自由液面高程η′差距不大；圓柱間距由S=0.5D增大到S=4D時，此時由于圓柱間距S等于一個波長(S=L)，圓柱之間的壅水效果降低，導致圓柱背風面測點B3(圖9c)自由液面高程較S=0.5D低；測點B2(圖9b)主要受下游圓柱2的反射波影響，具體表現在當圓柱間距由S=4D減小到S=0.5D時，下游圓柱2產生的反射波在與上游圓柱1產生的衍射波相互作用時起到一個抵消作用，最終導致測點B2處自由液面高程減小；同時還可以觀察到波浪在單個周期t′內自由液面η′演化曲線的不對稱性在增加.由此可知，圓柱迎風面(測點B1)主要受入射波直接作用的影響；當圓柱間距S減小時，圓柱背風面(測點B3)處因壅水效果增強，自由液面出現明顯抬升；圓柱側方(測點B2)受反射波的影響大，反射波與衍射波作用影響著測點附近自由液面的波動，自由液面演化曲線的不對稱性與此有關.

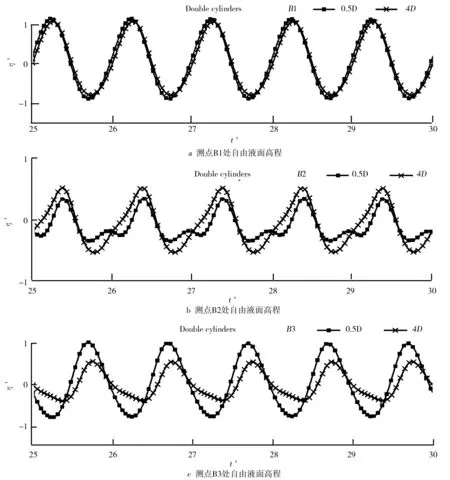
圖9 柱距為0.5D和4D下各測點單個周期t′內自由液面η′演化曲線

4 結論

基于不可壓縮的三維雷諾時均Navier-Stokes方程(RANS)，結合質量和動量守恒方程求解k-ω湍流模型.主要研究了圓柱間距對兩串聯豎直圓柱自由液面高程和波浪力的影響，得出結論：數值模型對單個豎直圓柱波浪力F′和部分測點自由液面η′隨時間t′的演化曲線做了準確預測，計算結果與Mo[5]的實驗結果吻合性較好.隨著柱間距的增大(S=4D)，下游圓柱壅水效果降低，兩串聯圓柱中，上游圓柱1的單周期t′內波浪力F′演化曲線與單圓柱的波浪力F′演化曲線貼合趨勢越來越好.隨著柱間距的減小(S=0.5D)，圓柱之間壅水效果增強，具體表現為上游圓柱背風面(測點B3)因壅水作用自由液面高程逐漸上升；而上游圓柱側方(測點B2)受到反射波與衍射波共同作用自由液面高程減小，同時在單個周期t′內自由液面高程η′演化曲線的不對稱在增加.