對轉槳推進的高速水下航行體實尺度自航計算與分析

黃永生，楊晨俊，董小倩

1 上海交通大學 海洋工程國家重點實驗室，上海 200240

2 高新船舶與深海開發裝備協同創新中心，上海 200240

0 引 言

快速性預報是水面船舶及水下航行體設計的重要環節之一，其傳統做法是在阻力、敞水及自航模型試驗的基礎上對阻力、伴流及敞水性能的尺度效應采用1978 ITTC規程等經驗方法進行修正。對于常規螺旋槳推進的船舶，采用該方法雖然可靠性好，但成本較高。高速水下航行體一般采用對轉槳（CRP）或泵噴推進，推進器部件間的相互作用給尺度效應修正帶來了一定的困難（主要是伴流）。另一方面，隨著計算流體力學（CFD）的快速發展，粘流CFD計算技術在快速性預報方面的應用日益增多，并有逐步取代模型試驗的趨勢。目前，阻力和敞水性能的數值計算精度已基本達到工程實用要求，自航計算的精度也在逐步提高。與模型試驗相比，粘流CFD計算技術的另一個優勢在于能夠進行實尺度模擬，從而無需進行尺度效應修正。實尺度模擬對計算機容量和速度的要求較高，其主要困難在于船體，而推進器則相對容易實現。

自航計算需要同時模擬船體與推進器，網格量和計算量均較大；從理論上看，需要進行非定常模擬，但所需計算時間會更長。因此，一般采用定常或準定常的方法模擬船體與推進器的相互作用。為了降低網格生成難度，節省計算時間，進行定常計算時可以采用體積力模型來代替螺旋槳的作用。體積力模型分描述型和迭代型2種，前者的體積力徑向分布形式是基于經驗公式，后者則是通過螺旋槳升力面、面元等勢流方法計算得到。基于描述型體積力模型，Choi等［1］對VLCC進行了自航模擬和快速性預報；傅慧萍［2］針對KCS進行了帶自由液面的自航模擬，研究了扭矩對計算精度的影響；呂曉軍等［3］開展了潛艇自航計算研究。Kim等［4］的研究表明，由于迭代型體積力模型是根據槳葉的真實幾何及實效伴流分布來計算體積力的分布，所以它對艉部流場的模擬比描述型體積力模型的結果更加準確。雖然采用體積力方法對自航因子的預報結果較好，但畢竟是用力場代替了真實槳葉，對于槳葉對周圍流體的排擠效應和擾動難以精確體現，從而限制了計算精度和流場細節。2005年以后，采用螺旋槳真實幾何的數值自航模擬方法逐步發展起來。Lübke［5］應用CFX軟件對KCS進行了自航模擬；Choi等［6］對一系列船型進行數值自航模擬和快速性預報，充分驗證了其計算方法的精度和可靠性；熊鷹等［7］則針對傅汝德數較低的排水型船舶提出了一種簡化的自由面處理方法，用以加快計算速度；楊琴等［8］針對配有七葉槳的SUBOFF潛艇進行了自航模擬，并分析給出了自航因子。上述自航模擬均是在模型尺度下進行，仍需通過修正尺度效應來預報實船快速性。隨著計算機硬件能力的提高，近年來，有關實尺度自航計算的研究逐步增多。Castro等［9］以KCS為對象開展了實尺度自航模擬，并研究了推進因子的尺度效應；李亮等［10］也對KCS開展了類似的研究。

目前，針對高速水下航行體推進性能方面的數值計算研究相對較少。何文生［11］較早地采用螺旋槳的真實幾何對高速水下航行體進行了RANS模擬，但受計算機能力的限制，簡化了附體。張濤等［12-13］針對對轉槳的敞水性能，開展了RANS計算研究。但是，針對高速水下航行體的自航計算研究，在模型和實尺度方面均未見公開發表的文獻。

為此，本文擬開展對轉槳推進的高速水下航行體實尺度自航CFD計算研究，基于阻力、敞水及自航模擬結果，分析自航因子。將計算處于深潛狀態的航行體，而不考慮自由液面和空化的影響。

1 計算方法

本文采用求解RANS方程的方法，來開展對轉槳推進的高速水下航行體自航性能實尺度計算研究。假定流體不可壓縮，流動為全湍流，采用標準k-ε湍流模型和非平衡壁面函數。控制方程包括連續性方程、動量輸運方程及湍流輸運方程，此處不再贅述。網格生成采用ICEMCFD及GAM?BIT軟件，數值計算采用FLUENT軟件。

1.1 計算域及其離散

如圖1所示（圖中D0為航行體平行中體段的直徑；L為航行體長度），阻力及自航計算域為包圍航行體的回轉體，但阻力計算域不包含前、后槳葉。將計算域劃分為4個子域：Fore-body和Rudder/fin為靜止域；Rotor-F和Rotor-A在阻力計算中為靜止域，在自航計算中為旋向相反的旋轉域。4個子域之間依次設有Int.mid，Int.aft和Int.CRP三對交界面。

子域Fore-body和Rudder/fin采用結構化單元離散，對航行體頭部及附體等幾何變化劇烈的區域進行了網格加密。用圓柱面CS將子域Rotor-F和Rotor-A分割為2個部分，其中CS的外部用結構化單元離散；用通過尾端面的橫截面XS進一步分割子域Rotor-A，其中CS內部和XS下游部分用棱柱單元離散。在自航計算中，CS內部以及包含前、后槳葉的區域采用四面體及五面體非結構化單元離散；在阻力計算中，原前、后槳葉所在區域用結構化單元離散。圖2所示為阻力、自航計算關鍵區域的物面/截面部分區域面網格。

如圖3所示，對轉槳的敞水計算采用圓柱形全流道計算域，圖中，DF為前槳直徑。前、后槳之間的交界面Int.CRP將計算域分為了2個旋轉方向相反的子域，每個旋轉域又進一步劃分為3個子域。其中子域Far-F和Far-A采用六面體結構化單元離散；包圍前槳及轂帽的子域Rotor-F和包圍后槳的子域Rotor-A采用四面體及五面體非結構化單元離散；子域UpS和DownS采用棱柱體單元離散。為了保證槳葉間網格的周期性，對于所有子域，在相鄰槳葉之間生成周期面，將全流道沿周向等分成Z（Z為槳葉數）個子流道，通過復制子流道網格、合并周期面網格，得到全流道網格。圖4所示為子域UpS，Rotor-F，Rotor-A及DownS的子流道幾何。

需要說明的是，本文的模型尺度及實尺度的計算均采用壁面函數，因此，需要根據計算對象的雷諾數，對航行體及槳葉、槳轂表面第1層單元采用合適的高度，以使壁面y+值處于可適用壁面函數的范圍，y+的具體數值見各算例。在阻力驗證計算中，模型尺度與實尺度的計算網格拓撲關系以及各子域的單元類型均完全相同；而在敞水驗證計算中，實尺度的計算網格由模型尺度網格按縮尺比（1∶1.5）放大得到。

1.2 計算設置

將航行體、推進器表面分別設為靜止和旋轉坐標系中的光滑無滑移壁面；計算域的下游邊界面設為壓力出口，其余邊界面設為速度入口。動量方程和湍流輸運方程采用二階迎風格式離散，壓力方程采用標準格式離散，壓力與速度的耦合采用SIMPLE算法。

阻力計算采用定常模型；敞水及自航計算分別采用準定常模型和非定常（滑移網格）模型，在非定常計算的每個時間步前、后槳葉各轉動1°。

實尺度自航計算在給定的航速下進行，通過調整轉速（前、后槳相等），直至螺旋槳推力與航行體阻力之差小于后者的1%，即認為達到了航行體的自航點，結束計算。在自航的非定常計算中，推力、阻力均為一個槳葉旋轉周期（360°）的時間平均值。敞水和自航的非定常計算收斂準則是，推力在連續2個旋轉周期內的時間平均值之差小于0.5%。

2 計算精度驗證

基于類似的航行體及對轉槳的模型試驗結果，分別驗證阻力和敞水性能的數值計算精度；同時，進行實尺度計算，定性分析相關結果的合理性。因缺乏試驗數據，對高速水下航行體的自航計算精度目前還無法驗證。

2.1 航行體阻力

以圖5所示的航行體為對象，驗證阻力計算精度。在網格依賴性檢驗的基礎上，先進行模型尺度的計算，對比試驗數據以驗證計算精度；然后，進行實尺度計算，并根據模型試驗結果對實尺度阻力進行預報，間接驗證實尺度阻力的RANS計算精度。

2.1.1 網格依賴性檢驗

為保證壁面y+值基本相同，采用相同的單元徑向尺度，沿航行體軸向和周向按2∶2∶1的尺度比由疏到密建立3套網格M1，M2和M3，然后在模型尺度下進行了2個航速的阻力計算，雷諾數Rem分別為1.220×107和2.034×107，壁面y+的平均值均約為50。表1所示為3套網格參數的比較。航行體總阻力系數Ctm隨網格尺度的變化如圖6所示。隨著網格的加密，Ctm趨于收斂；M2網格與M3網格Ctm的相對差僅為0.4%。因此，后續阻力計算采用M2網格的尺度，以兼顧計算精度和效率。

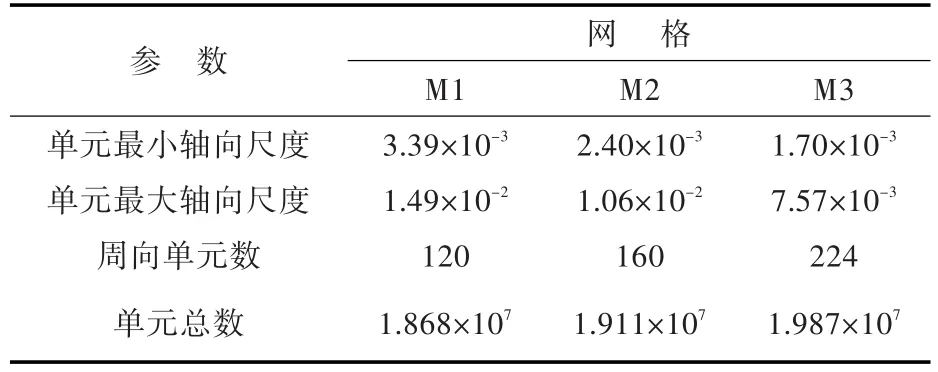
表1 3套阻力計算網格參數的比較Table 1 Comparison of the parameters for three sets of grids of resistance computation

2.1.2 模型和實尺度阻力計算精度驗證

首先，驗證模型尺度的阻力計算精度。表2所示為RANS計算結果與模型試驗結果的比較。由于附體與殼體相比面積很小，因此分析形狀因子時未區分殼體與附體，即

對模型試驗，摩擦阻力系數Cfm按1957 ITTC公式計算：

對于RANS計算，Cfm直接采用計算結果。在計算雷諾數的范圍內，模型總阻力計算值總體上低于試驗值，但誤差不超過3%；摩擦阻力的計算誤差不超過3.5%，且隨著航速的增高誤差減小，這可能是因為計算是在全湍流狀態下進行，而模型試驗雖然采取了激流措施，但在航速較低時仍受到層流及過渡區的影響；形狀因子的計算誤差不超過4%。

實尺度網格拓撲與模型尺度相同，計算單元總數為1 985萬。雷諾數Res=1.682×108，壁面y+平均值約為50。表3所示為實尺度航行體阻力的RANS計算結果與基于模型試驗的預報結果間的比較，用于對實尺度阻力計算精度的間接驗證。在預報中，忽略了形狀因子的尺度效應，實尺度的形狀因子(1+k)s為表2中模型試驗雷諾數范圍內(1+k)m的算術平均值，Cfs按1957 ITTC公式計算，Cts等于(1+k)s與Cfs的乘積，為航行體總阻力系數。在RANS計算結果分析中，Cfs和Cts均為直接計算值，(1+k)s為Cts與Cfs的比值。由表3可見，實尺度航行體總阻力的RANS計算值略低于基于模型試驗的預報值，誤差為3.3%。

表2 模型尺度航行體阻力RANS計算與試驗的比較Table 2 Comparison of RANS-simulated model-scale resistance of the underwater vehicle with experimental data

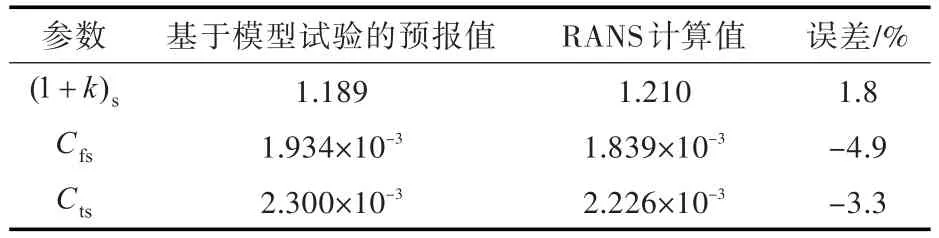
表3 實尺度航行體阻力的RANS計算結果與基于模型試驗的預報結果間的比較Table 3 Comparison between RANS-simulated full-scale resistance ofthe underwater vehicle and that predicted from model test results

2.2 對轉槳敞水性能

以某高速航行體對轉槳為對象，驗證敞水性能的RANS計算精度。該對轉槳前槳11葉、后槳9葉，前、后槳的直徑之比為1.062。首先，進行模型尺度的網格依賴性分析，確定合適的網格尺度；然后，進行模型尺度和實尺度敞水性能的計算與試驗比較。

2.2.1 網格依賴性檢驗

計算在模型尺度進行，進速系數J=1.0和1.4時，如式（3）所示的0.7R（R為槳直徑）處雷諾數分別為8.45×105和9.05×105。

式中：VA為進速；b0.7R，n和D分別為槳葉0.7R處的弦長、轉速與直徑；ν為水的運動粘性系數。由疏到密建立了3套網格G1，G2和G3，其單元尺度之比為2∶2∶1，面單元和體單元的密度分布及增長率保持不變。表4所示為3套網格的參數比較，其中面單元相對尺度為面單元尺度與前槳直徑的比值。

表5所示為網格尺度不同引起推力系數KT和扭矩系數KQ計算結果的相對變化。表中KT和KQ均以前槳的直徑無量綱化，下標F和A分別表示前、后槳。分別用R1，R2和R3代表G1，G2，G3的KT或KQ計算結果，則表中C21=R2/R1-1，表示R2相對R1的變化，C32=R3/R2-1，表示R3相對R2的變化。從表中可以看出，前、后槳的推力和扭矩基本上是隨網格尺度的減小而減小；3套網格計算結果之差均在1.2%以內。經權衡精度與效率，后續的計算采用G2網格的尺度。

表4 3套敞水計算網格參數的比較Table 4 Comparison of the parameters for three sets of grids of open-water computation

表5 敞水性能計算結果隨網格尺度的相對變化Table 5 Influence of grid size on computed open-water performance

2.2.2 敞水性能計算

用于驗證的對轉槳模型與實槳的尺度比為1∶1.5，實槳的計算網格由槳模網格放大得到。在計算工況范圍內，槳模與實槳在0.7R處的雷諾數分別為8.45×105～9.05×105和3.17×106～3.39×106，槳葉表面的y+平均值分別為35～50和130～200，均在壁面函數的適用范圍內。當前、后槳的葉數相互不構成整倍數關系時，兩者相互作用的非定常性很弱［14］，非定常計算結果的時間平均值與準定常結果很接近，因此采用準定常計算以節約計算時間。

圖7所示為敞水性能的模型和實尺度RANS計算結果與模型試驗結果比較，圖中η0為敞水效率，下標F和A分別表示前、后槳。在計算進速系數范圍內，總推力系數和總扭矩系數的計算誤差分別小于2%和4%，表明模型尺度RANS計算具有較高的精度。比較實尺度與模型尺度的RANS計算結果發現，KT的變化很小，而KQ則有較明顯的降低，導致實槳的敞水效率比模型槳的高2.5%左右，該結果與單槳敞水性能尺度效應定性一致，表明對轉槳實尺度敞水性能的RANS計算方法比較可靠。

3 實尺度自航計算與分析

基于上述計算方法，對采用對轉槳推進的某高速水下航行體進行實尺度阻力、敞水及自航計算，并分析其推進因子。對轉槳的前槳9葉、右旋，后槳7葉、左旋，二者轉速相同。

3.1 航行體阻力計算

阻力計算單元總數約1 127萬。計算航速范圍為設計航速的64%～109%，雷諾數為8.07×107～13.83×107，航行體壁面y+的平均值約為50。圖8所示為該航行體實尺度阻力的RANS計算模型，圖9所示為拖航阻力系數計算結果。圖10所示為航行體摩擦阻力系數的RANS結果與1957 ITTC公式計算結果的比較，由圖可見，前者略高，兩者間的差異隨航速的增大而減小，在設計航速下相差1.9%。圖11所示為形狀因子(1+k)s隨航速的變化，雖然形狀因子隨航速的增高而變大，但在計算航速范圍內其差值小于1%。

3.2 對轉槳敞水性能計算

敞水計算單元總數約為4 634萬，槳葉0.7R處雷諾數范圍為2.38×106～2.57×106，槳葉表面y+的平均值約為210。分別采用準定常和非定常方法模擬前、后槳之間的相互作用，其中準定常方法用于模擬槳葉旋轉過程中某一瞬間的流動，而非定常方法則是在時域中模擬槳葉旋轉過程中的流動。圖12和圖13所示分別為實尺度對轉槳敞水性能的RANS計算模型和計算結果，其中非定常方法模擬的結果為槳葉旋轉一周的平均值，圖中扭矩系數KQ的第2下標0表示敞水，以與后文中的自航數據相區別。從圖13中可以看出，采用準定常方法與非定常方法模擬的敞水性能結果非常接近，差值在1%以內。

3.3 自航計算結果

自航計算在設計航速下進行，計算單元總數為4 827萬，航行體雷諾數為12.69×107，壁面y+的平均值約為50。分別采用準定常和非定常方法進行計算，自航轉速根據1.2節所述方法確定。圖14所示為自航的RANS計算模型。為了節約計算時間，非定常計算采用準定常計算得到的自航轉速及流場作為初始值。圖15所示為非定常計算的軸向力收斂歷程。圖中，KQBF和KQBA分別為前、后槳的扭矩系數。其中推力系數和扭矩系數的脈動幅值分別為各自平均值的0.2%與0.1%，而Cts的脈動幅值則約為平均值的2.5%。Cts的脈動主要源于由槳葉尾流引起的航行體尾端面壓力脈動。

自航的非定常與準定常計算結果間的比較見表6，表中Ns為航行體推力和阻力平衡時前、后槳的轉速（兩者相等）。由于航行體伴流不均勻性的影響，自航非定常計算與準定常計算結果間的差別比敞水情況下的大，主要表現為非定常計算的后槳負荷比準定常的高。從理論上講，非定常計算模型更接近于物理實際，因此在前、后槳扭矩平衡要求較高的設計場合，采用非定常計算相對可靠。

表6 自航計算的準定常與非定常計算結果的相對差Table 6 Relative difference between quasi-steady and unsteady results of self-propulsion simulation

圖16所示為自航狀態基于Q準則的尾部渦流形態（準定常結果）。從圖中可以看出，在槳葉邊緣、附體的尾緣和航行體尾端面均出現了明顯的渦流，較合理地反映了槳葉對周圍流場的擾動。由于前、后槳旋轉域間交界面上的網格無法做到相同，因此前槳尾渦在進入后槳域后因網格耗散幾乎消失了。

圖17所示為在尾端面下游0.05倍前槳直徑處，橫截面內切向速度沿半徑的分布。其中，切向速度為沿圓周線的平均值，并用當地半徑槳葉的旋轉線速度進行無量綱化。所謂當地半徑，是指在航行體中縱剖面上，將通過前、后槳盤半徑外端點的線段延長到該縱向位置，線段終點與航行體軸線的距離。圖17中的橫坐標為徑向相對坐標2r/DF，其中r為徑向坐標值。0.65R至葉梢的切向速度幾乎為零，但內半徑的切向速度仍有殘留。總體來看，在設計航速下，該航行體尾流基本沒有旋轉，表明前、后槳的扭矩平衡較好。

3.4 自航因子分析

綜合阻力、敞水及自航計算結果，采用等推力法進行自航因子分析，結果如表7所示。表中：J0為根據KT在圖13對應的推力系數曲線上插值得到的進速系數；η0為J0所對應的效率曲線上的值；KQ的第2下標B表示自航狀態，用于與敞水狀態的0相區別；ηR為相對旋轉效率；ηD為推進效率；下標F和A分別表示前槳和后槳。

表7 自航分析結果Table 7 Results of self-propulsion analysis

分析比較表明：

1）自航因子計算值處于合理的范圍。參考文獻［15］，水下航行體的伴流分數w和推力減額系數（1-t）的范圍分別為0.10～0.25和0.82～0.90，本文中航行體的計算結果也處于此范圍內。

2）前槳的伴流分數高、后槳的伴流分數低，分析原因認為主要為：一是前槳更靠近尾附體，附體的尾流速度虧缺量更大；二是前、后槳轂徑之比為1.31，而直徑之比僅為1.06，這就意味著前槳盤面有較多的面積處于槳轂邊界層中。此外，槳葉的抽吸作用會導致槳盤面處的實效伴流低于標稱伴流，如果這種作用在槳盤前較弱、槳盤后較強，也會成為原因之一，不過該問題還有待進一步的研究。

3）推進因子及推進效率的準定常與非定常計算結果間的誤差在2%以內。若采用準定常計算方法得到的推力減額較低、推進效率較高，則有可能導致設計槳偏重，預報的航速偏高。

4 結 論

本文通過求解RANS方程，對采用對轉槳推進的高速水下航行體開展了實尺度自航計算與分析研究。通過與模型試驗結果的比較，驗證了在航行體阻力和對轉槳敞水性能方面，采用本文方法計算精度良好；間接的驗證及定性分析表明，實尺度阻力和敞水的計算結果合理、計算方法可靠，但實尺度自航計算仍有待驗證。對某航行體實尺度的自航計算與分析表明：

1）采用準定常和非定常方法計算得到的推進因子其數值比較接近，也在合理范圍內，可望為高速水下航行體對轉槳設計提供較可靠的輸入，從而提高設計精度、減少模型試驗，縮短設計周期。

2）在自航模擬中，準定常計算方法具有精度合理、計算量小的優點，比較適合工程應用；但當航速預報精度以及前、后槳的扭矩平衡精度要求較高時，采用非定常計算方法更合理。