井下導線測量及陀螺定向測量的精度分析探討

張 潔

(大同煤礦集團 馬道頭煤業有限責任公司，山西 大同 037100)

煤礦井下巷道開拓前，需要進行必要的導線測量工作來規劃指導井下巷道的現場施工，以期滿足設計圖紙的精度要求。在進行井下導線測量時，必然有可能產生各種誤差，因此有必要對產生的各種誤差進行分析、總結以及了解誤差累計的規律，進而采取有效的措施來減小甚至消除這種誤差，從而為礦井井下開拓工程奠定堅實的基礎。

1 導線測量誤差分析

采用導線測量控制井下開拓巷道的掘進精度時，需要對導線的水平角、豎直角和邊長三要素進行綜合測量。根據以往經驗和文獻研究可知，實際導線測量工作中邊長和豎直角的測量一般均能滿足測量的精度要求，因此著重對水平角測量精度進行分析研究。

水平角測量的精度誤差主要由測量儀器本身的誤差、測量方法的誤差以及對中誤差所致。其中：

（1）測量儀器本身的誤差誘因有多方面，例如儀器零件的加工誤差、組裝和校核誤差、儀器結構誤差和穩定性等因素。

（2）測量方法的誤差主要是由于人為的原因造成的，其誤差值大小如式(1)所示。

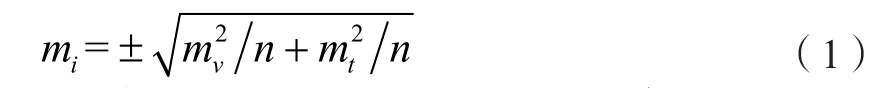
式中構成測量方法誤差的核心因素主要由照準誤差mv、讀數誤差mt和測回數n組成。

（3）對中誤差由全站儀和其前后的棱鏡對中線測量誤差所致，進一步導致水平角的測量誤差。

2 導線測量誤差計算

水平角測量精度可以通過測角中誤差這一數值指標來反饋，而測角中誤差又可以根據多個雙次觀測值的方法求出。假設每次測量結果等精度，則可以利用兩次觀測值的差值來計算測角中誤差，如式（2）所示。

式中：d為兩次同精度測量結果的差值，n為兩次測量導線上差值的個數，且差值盡量在不同的導線上選取，并且盡量使差值的數量最大化。

為了提高測量結果的可靠性，可以選取多組導線進行雙次觀測值的計算，并取多個雙次觀測值結果進行平均，計算公式如式（3）所示。

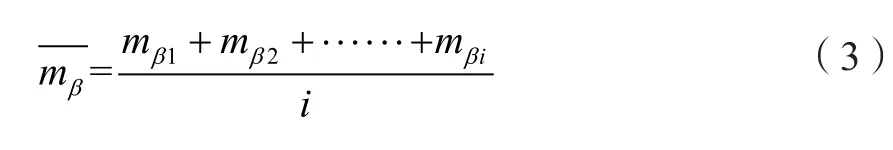
式中：mβi為第i次雙次觀測值結果，i值越大則測角中誤差值的計算結果越精確。

以山西馬道頭礦為例，由于該礦井回風大巷關鍵線路施工段現場施工時進行了多次重復測量，構成了可以采取雙次觀測值的方法來計算測角中誤差的前提條件。采用雙次觀測值測量方法時，在兩條相互獨立的導線上分別選取了8組點進行差值計算，其差值變化情況以及測角中誤差計算結果如圖1所示。從圖中可以看出，除了第7組測點的差值和相應的測角中誤差值波動性比較大以外，其余測點的差值和相應的中誤差值變化波動性均較小，其測角中誤差平均值為5.2″，滿足安全規程要求的測角中誤差小于7″的規定，但是比較接近規定的臨近值大小，說明測量結果精度較低，雖然能夠滿足測量要求，但測量結果對工程質量的精度控制度不高。

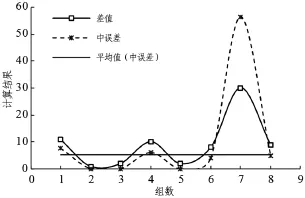
圖1 雙次觀測值法測量結果分析

3 陀螺定向測量精度分析

陀螺儀本身為一種具有測定真北方位的精密儀器，將其與經緯儀組合形成的陀螺經緯儀能夠不受時間和環境的限制，并且具有操作簡單、測量效率高等優點，因此在礦山井下測量中采用陀螺經緯儀能夠有效地提高測量的效率和測量的精度。

根據白塞爾公式計算陀螺經緯儀一次測定的測角中誤差計算公式如式（4）所示。

式中：

v-1次測回的數值，為了確保測量計算結果的精確性，一般進行5次測回取平均值。

同樣以該礦井回風大巷關鍵線路施工測量為背景，采用首級±15″的陀螺經緯儀進行測定，共進行5次測回，每次測回分為左右兩側各一次，并對5次測回結果取平均值，測定結果如圖2所示。從圖中可知，5次測量值根據公式（4）計算的測角中誤差的平均值為2.74″，遠遠滿足首級±15″的精度要求，且測角中誤差值遠遠小于采取導線測量的結果，幾乎是采用導線測量方法測定結果的一半，這說明采用陀螺經緯儀定向測量能夠有效地提高測量的精度，進而更好地對現場工程質量的精度進行控制。

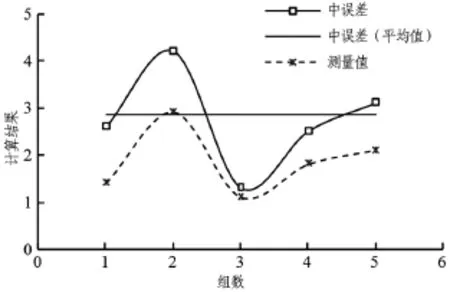
圖2 陀螺定向測量結果分析

4 結論

傳統的井下導線測量雖然能夠滿足安全規定的測量精度，但其測量精度較低，且誤差主要來源于水平角測量誤差。由于水平角測量精度可以通過測角中誤差這一數值指標來反饋，因此對山西馬道頭礦回風大巷關鍵線路采用導線測量和陀螺定向測量計算結果進行對比，可知導線測量的測角中誤差為5.2″，而采用陀螺經緯儀測量的測角中誤差為2.74″，測角中誤差幾乎為導線測量結果的一半，說明采用陀螺定向測量能夠有效地提高測量的精度，對礦井重要巷道的施工開拓有重要的規劃指導意義。