高頻擾動下的雙饋風機系統頻率響應及其振蕩風險分析

吳 雨，薛安成，付瀟宇，王子哲

（1.國網江蘇省電力有限公司無錫供電公司，江蘇 無錫 214000；2.新能源電力系統國家重點實驗室（華北電力大學），北京 102206）

0 引言

近年來，隨著新能源發電裝機容量的逐年攀升，大量的電力電子設備接入電力系統，使得電網運行特性和控制特性變得非常復雜[1]，由此產生了一系列新的振蕩問題，其中，發生在直流外送系統中的中高頻段振蕩問題尤其受到學者關注。文獻[2]分析了德國北海風電場發生的250～350 Hz高頻振蕩現象。文獻[3-5]提及舟山五端直流輸電工程的中高頻分量（以二次諧波為主）導致跳閘的事件。文獻[6]分析了魯西直流工程發生的1.2 kHz左右高頻振蕩現象。文獻[7]針對高壓直流系統中發生的高頻振蕩，提出采用特征根法來分析系統等效參數、穩態運行點等關鍵因素對振蕩的影響，從而為振蕩的抑制提供理論依據。

另一方面，大規模新能源經直流外送是當前趨勢之一，因此，雙饋/直驅風機等主要的新能源發電設備可能會感受到來自外送系統的高頻擾動，并響應放大，形成振蕩問題。然而，值得注意的是，對于外界周期擾動的響應，現有研究主要集中在次同步頻率擾動下的響應傳播機理問題[8-11]，如文獻[8]分析并推導了次同步振蕩電流在MMCHVDC（基于模塊化多電平換流器的高壓直流輸電）系統中的分布及傳播機制；文獻[9]詳細推導并分析了轉子繞組中的單個頻率擾動電壓在定子繞組中感應出單個主要頻率的響應電流的頻率和幅值；文獻[10]、文獻[11]分別分析了次同步振蕩電流在永磁直驅風機系統和雙饋風機各環節的傳播與響應機理。而對于高頻擾動下的雙饋/直驅風機系統響應問題目前鮮有報道。

此外，對于雙饋風機的阻抗頻率特性分析主要集中在次同步段，而對高頻段很少關注。如文獻[12-14]基于雙饋風機的阻抗特性分析了雙饋風機-串補系統的次同步振蕩機理及其影響因素。

對此，本文研究了高頻擾動下雙饋風機系統的多頻率響應，并對其振蕩風險進行了初步分析。首先，基于高頻擾動信號的響應路徑，定性推導并分析了受控異步機系統/網側換流器系統各環節的頻率響應，獲得了受控異步機系統/網側換流器注入系統的各頻率響應，揭示了整個雙饋風機系統在并網點輸出受高頻擾動下的電流多頻率響應。進而通過掃頻法和阻抗法分析了200～1 100 Hz高頻段內雙饋風機系統的阻抗頻率特性，驗證了基于簡化模型的阻抗法的有效性，并初步評估了雙饋風機系統高頻振蕩風險。

1 雙饋風機系統多頻率響應分析

1.1 響應機理分析

根據文獻[11]的推導和定義，雙饋風機系統分為受控異步機系統（含轉子側換流器）和網側換流器系統。

當并網點存在頻率為fp的高頻擾動信號時：

（1）受控異步機系統（運行在工頻f1下，轉速頻率為fm）最終在轉子側繞組中產生頻率為fp-fm，fp-2f1+fm，2fp-f1-fm，2fp-3f1+fm的電壓和電流擾動分量，其中fp-2f1+fm分量幅值大于2fp-f1-fm和2fp-3f1+fm分量幅值；在定子側繞組中會產生fp，fp-2f1，2fp-f1，2fp-3f1頻率的電流擾動分量并注入并網點，其中fp-2f1分量幅值大于2fp-f1和2fp-3f1分量幅值。如表1所示。

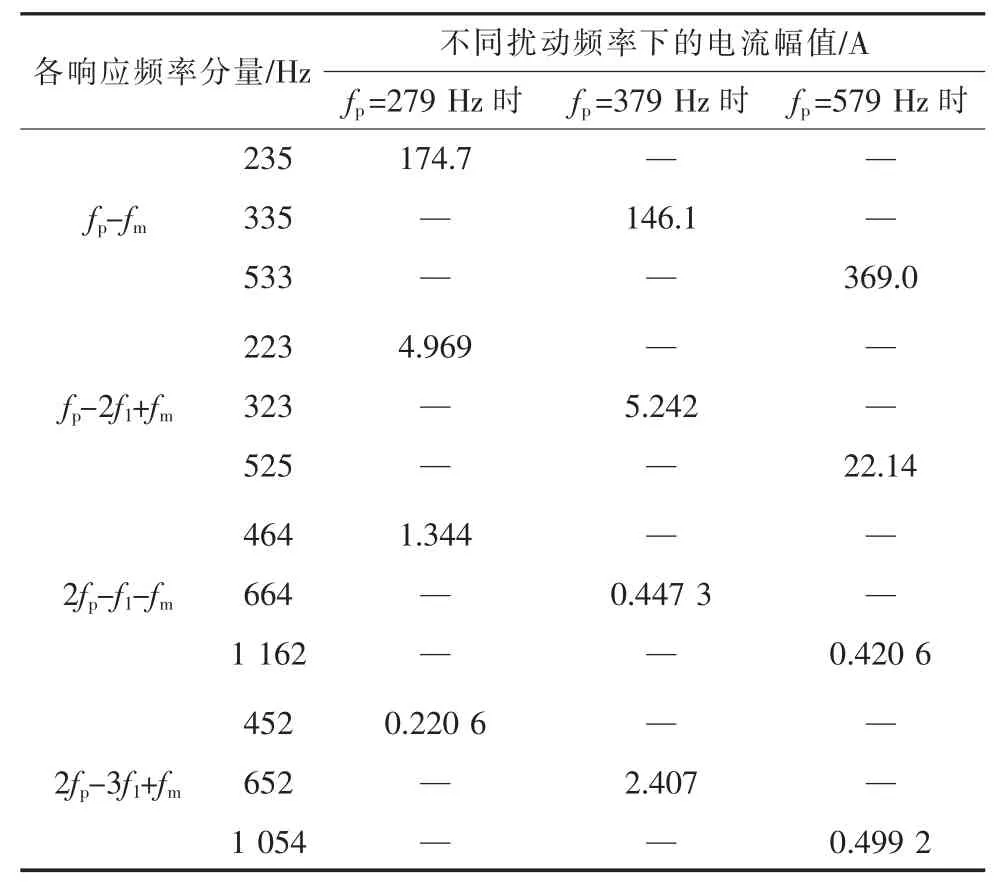
表1 轉子a相電流的頻率響應

（2）網側換流器系統會向并網點輸出頻率為fp， fp-2f1， 2fp-f1， 2fp-3f1的電流擾動分量。

（3）整個雙饋風機系統會向并網點輸出頻率為fp，fp-2f1，2fp-f1和2fp-3f1的電流擾動分量。

1.2 仿真驗證

在PSCAD中搭建了并網雙饋風機系統模型，仿真分析不同頻率高頻擾動下的系統頻率特性。擾動頻率fp分別設置為 279 Hz，379 Hz和579 Hz，轉子轉速頻率fm分別設置為44 Hz和46 Hz。

不同頻率的高頻擾動下，轉子a相電流各主要頻率響應分量的幅值如表2所示，其中279 Hz擾動下轉子a相電流的對數幅頻特性如圖1所示。

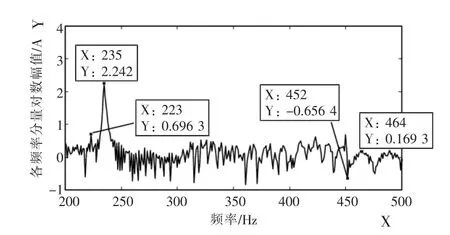
圖1 轉子a相電流的頻譜特性

圖1表明，當系統存在頻率為279 Hz的高頻擾動時，轉子a相電流存在235 Hz（fp-fm），223 Hz（fp-2f1+fm）， 464 Hz（2fp-f1-fm）， 452 Hz（2fp-3f1+fm）的頻率分量。其中，235 Hz為主要的響應頻率分量；223 Hz分量幅值比平常的噪聲大，較明顯；而464 Hz和452 Hz分量含量較小，淹沒在噪聲中。同時，結合表1可知，轉子a相電流的2fpf1-fm和2fp-3f1+fm分量幅值明顯小于fp-2f1+fm分量幅值，與理論分析結果一致。

圖2—4分別為受控異步機子系統、網側換流器子系統和雙饋風機系統輸出電流的對數幅頻特性，三者均包含 179 Hz（fp），279 Hz（fp-2f1），508 Hz（2fp-f1）， 408 Hz（2fp-3f1）的頻率響應， 這與理論分析結果一致。其中，定子a相電流的179 Hz分量幅值比平常的噪聲大，較明顯；而408 Hz和508 Hz的頻率分量量級很小，淹沒在噪聲里；網側換流器和并網點a相總電流的各分量幅值均比平常的噪聲大，較明顯。

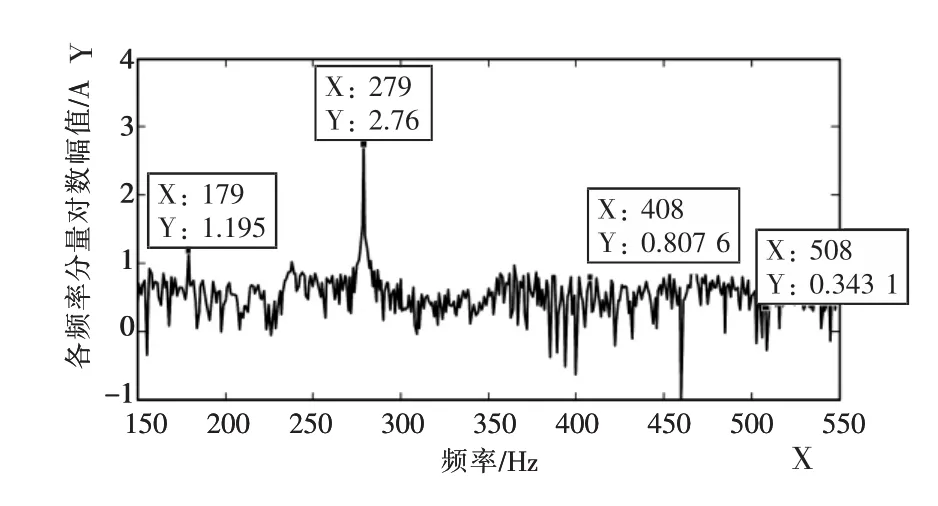
圖2 定子a相電流的頻譜特性

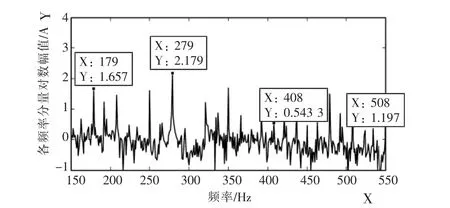
圖3 換流器出口a相電流的頻譜特性

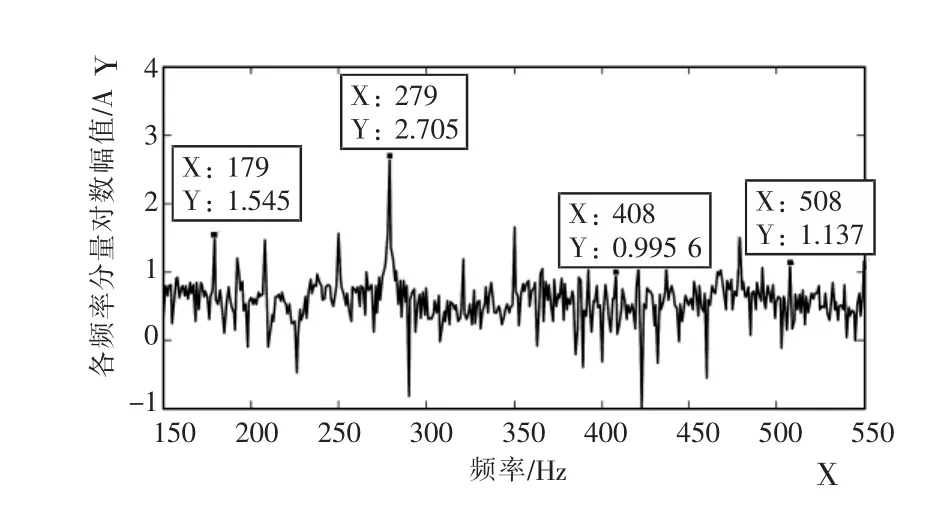
圖4 并網點a相總電流的頻譜特性

同時，結合表2可知，三者輸出電流的2fpf1，2fp-3f1分量幅值均小于fp-2f1分量幅值，這也與理論分析結果一致。

此外，雙饋風機向并網點輸出的電流多頻率響應主要來自于網側環流器系統，且擾動頻率越高，網側換流器系統產生的響應比重越大。

2 雙饋風機系統高頻振蕩風險分析

由前文分析可知，雙饋系統在高頻下對應的輸出穩定與否，決定了系統是否會發生高頻振蕩。目前，設備阻抗頻率特性分析是判斷系統振蕩風險的常用方法，因此，為實現快速評估振蕩風險，本節建立了雙饋風機的簡化阻抗模型，并與掃頻法所得阻抗進行對比，以驗證理論模型的準確性。之后基于該簡化模型可實現雙饋風機在高頻段振蕩風險的初步評估。

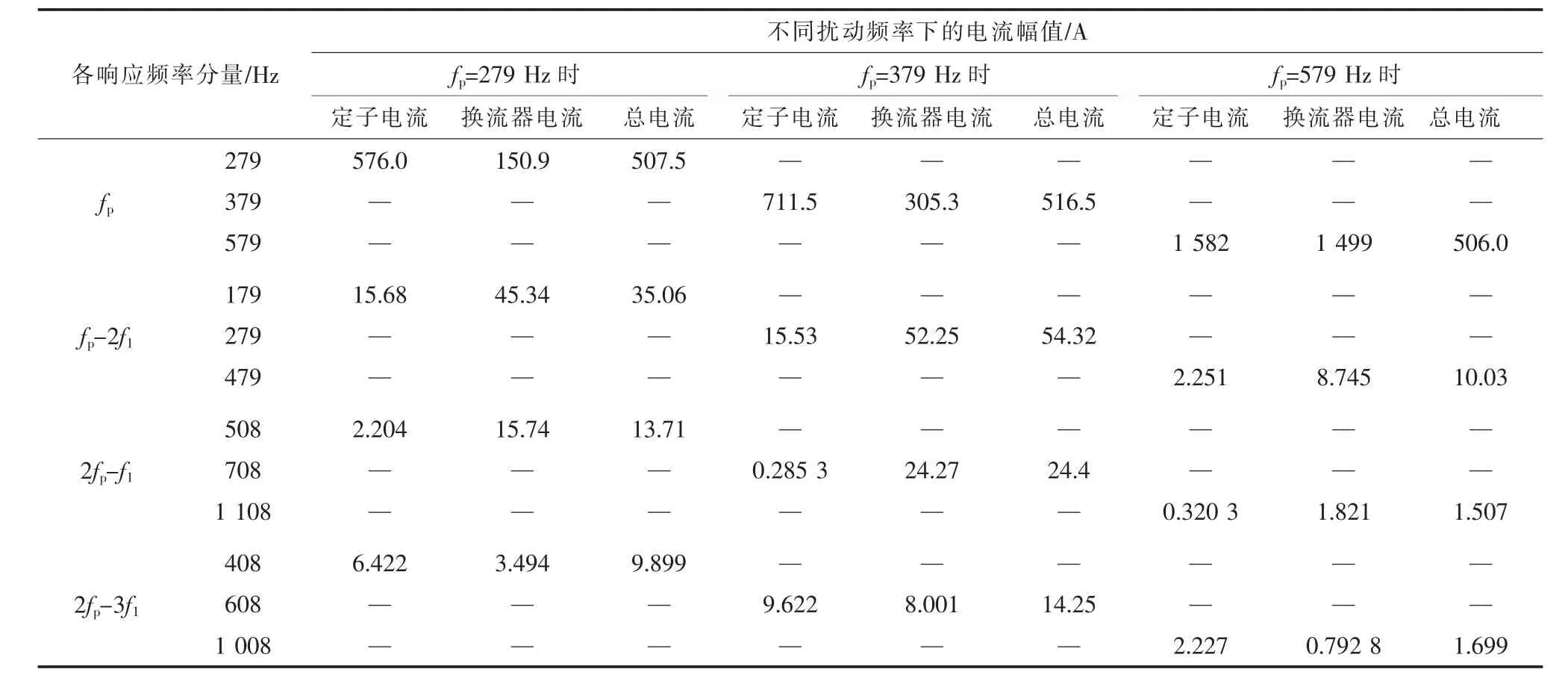
表2 雙饋風機系統輸出的電流頻率響應

2.1 雙饋風機系統阻抗建模

雙饋風機阻抗（ZDFIG）由受控異步機系統阻抗（ZCAMS）和網側換流器系統阻抗（ZGSCS）并聯構成，如式（1）所示。

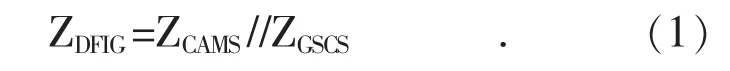
2.1.1 受控異步機系統阻抗模型

對于受控異步機阻抗，采用文獻[12]中的簡化阻抗模型，即不考慮RSC（轉子側換流器）的外環控制以及鎖相環的動態過程，如式（2）所示：

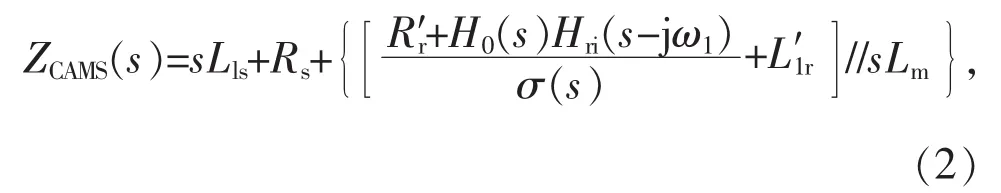
式中：Rs，Lls分別為定子繞組電阻和漏抗電感；Lm為感應電機的勵磁電抗電感；分別為折合到定子側的轉子繞組電阻和漏抗電感；ω1為振蕩角頻率， ω1=2πf1， f1為振蕩頻率； σ（s）為轉差率；Hri（s-jω1）為 RSC 電流內環的傳遞函數； H0（s）為RSC換流器指令值到出口值的傳遞函數。

其中：

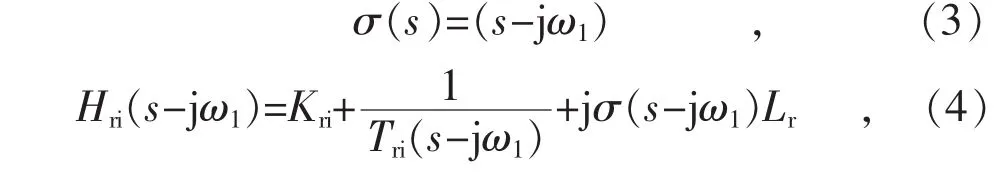
式中：Kri，Tri分別為雙饋風機RSC電流內環的比例參數和積分參數； σ（s-jω1）Lr為 RSC 電流內環dq軸控制解耦項系數。

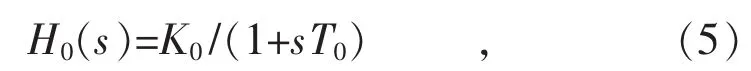
式中：K0，T0分別為一階滯后環節的比例參數和時間常數。

2.1.2 網側換流器系統阻抗模型

網側換流器系統阻抗（ZGSCS）由GSC（網側換流器）阻抗（ZGSC）和濾波器阻抗構成，類似于受控異步機系統，其阻抗模型如式（6）所示：

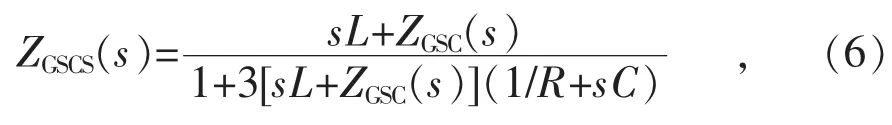
式中：R，L，C分別為網側換流器出口濾波器中的電阻、電感、電容。

濾波器結構如圖5所示。

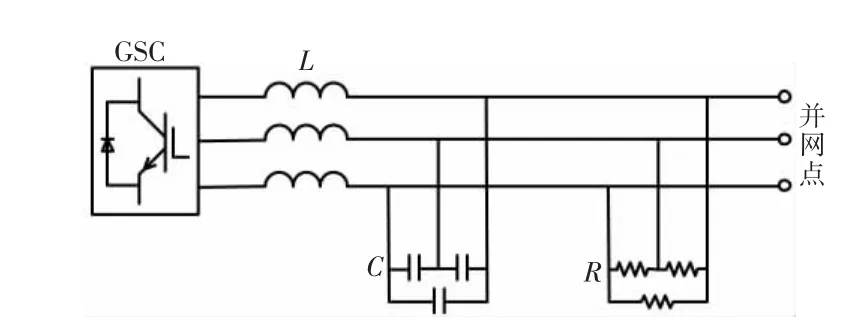
圖5 GSC出口濾波器示意

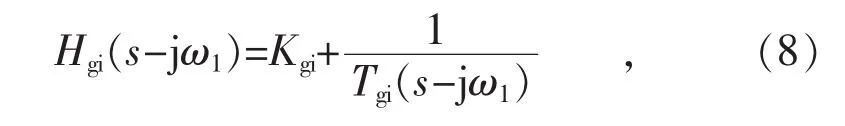
式中：Kgi，Tgi分別為雙饋風機轉子側換流器電流內環的比例參數和積分參數。

式中：K1，T1分別為一階滯后環節的比例參數和時間常數。

2.2 振蕩風險分析

根據式（1）、 式（2）、 式（6）確定的雙饋風機阻抗模型，計算并繪制出受控異步機系統、網側換流器系統以及整個雙饋風機的阻抗頻率特性，并與掃頻法所得結果進行比較，見圖6。

網側換流器阻抗如式（7）所示：

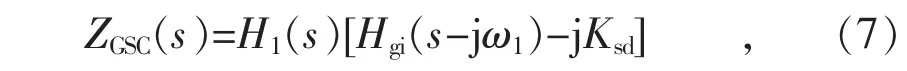
式中：Ksd為GSC電流內環dq軸控制解耦項系數；Hgi（s-jω1）為 RSC 電流內環 PI（比例-積分）環節的傳遞函數；H1（s）為RSC換流器指令值到出口值的傳遞函數。

其中：

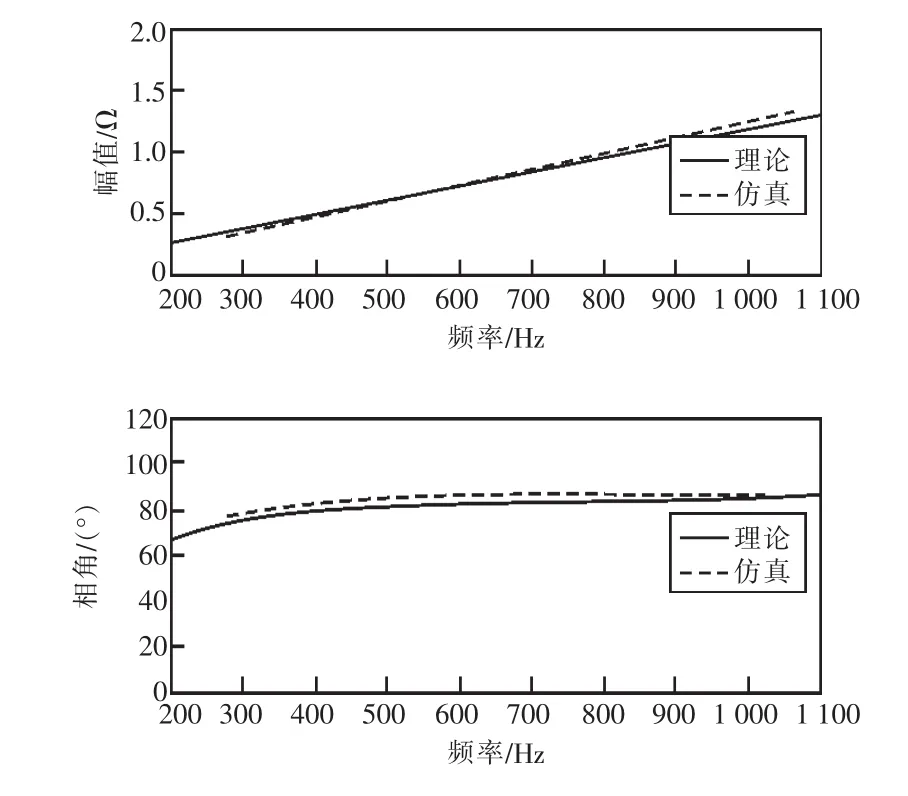
圖6 受控異步機系統阻抗頻率特性

2.2.1 受控異步機系統阻抗頻率特性分析

表3表明，理論計算阻抗與仿真所測阻抗的誤差在1 000 Hz附近較大，這是由于受控異步機系統在高頻段其結構和參數發生明顯的改變，如存在較多的雜散電容，而建模過程中未考慮這些因素，但總的來說，最大誤差在7%內，因此上述頻段內受控異步機系統阻抗模型具有較高的準確性。

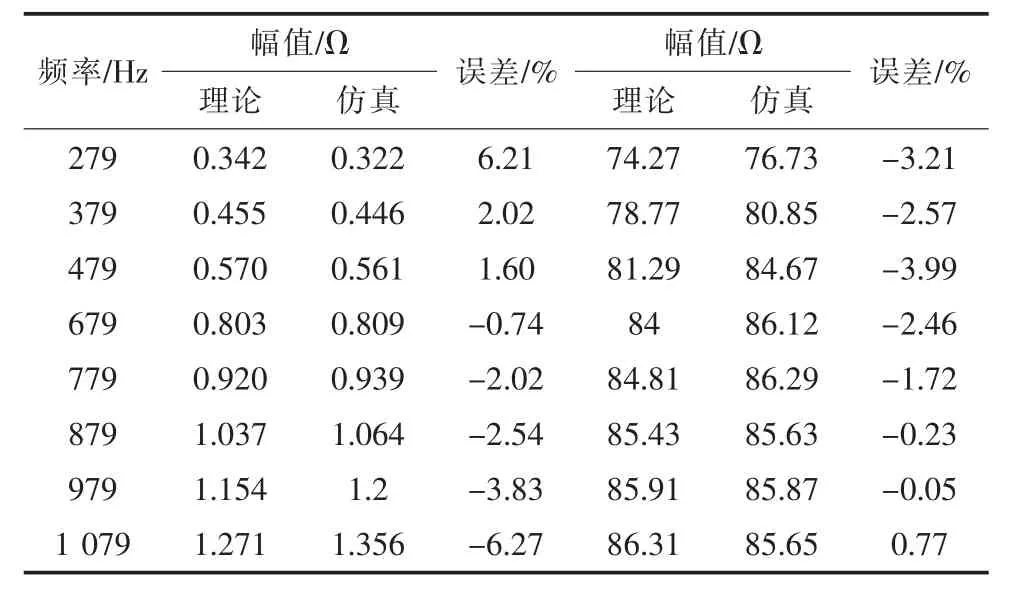
表3 受控異步機系統阻抗

同時，結合圖6可知，在200～1 100 Hz頻段內，受控異步機系統阻抗呈現正電阻-電感性質，且隨著頻率的增大，受控異步機系統阻抗模值近似線性增大。

2.2.2 網側換流器阻抗頻率特性分析

圖7和表4為網側換流器系統的理論計算和掃頻法所得阻抗頻率特性對比。表4表明，在200～400 Hz和 800～1 100 Hz范圍內阻抗模值的理論計算結果與仿真結果誤差在10%內，相角的誤差也在12%以內；而在400～800 Hz頻段內阻抗模值誤差最大可達27.92%，因此，網側換流器系統阻抗模型在200～400 Hz和800～1 100 Hz頻段內的有較高的準確性，而在400～800 Hz頻段內則誤差較大。該誤差是由于忽略鎖相環引起的，具體而言，本文中鎖相環的帶寬在400～800 Hz的范圍內，因此在該頻段內對網側換流器模型具有較大影響。

同時，結合圖7和表4可知，在200～1 100 Hz頻段內，網側換流器系統阻抗呈現正電阻-電容性質，且隨著頻率的增大，網側換流器系統阻抗模值減小。

2.2.3 雙饋風機系統阻抗頻率特性分析

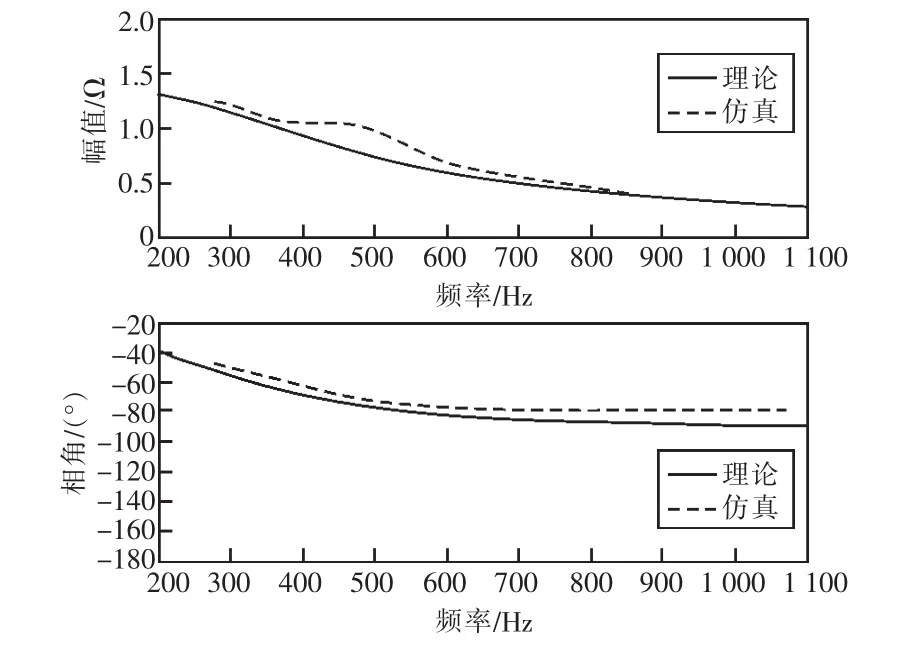
圖7 網側換流器系統阻抗頻率特性

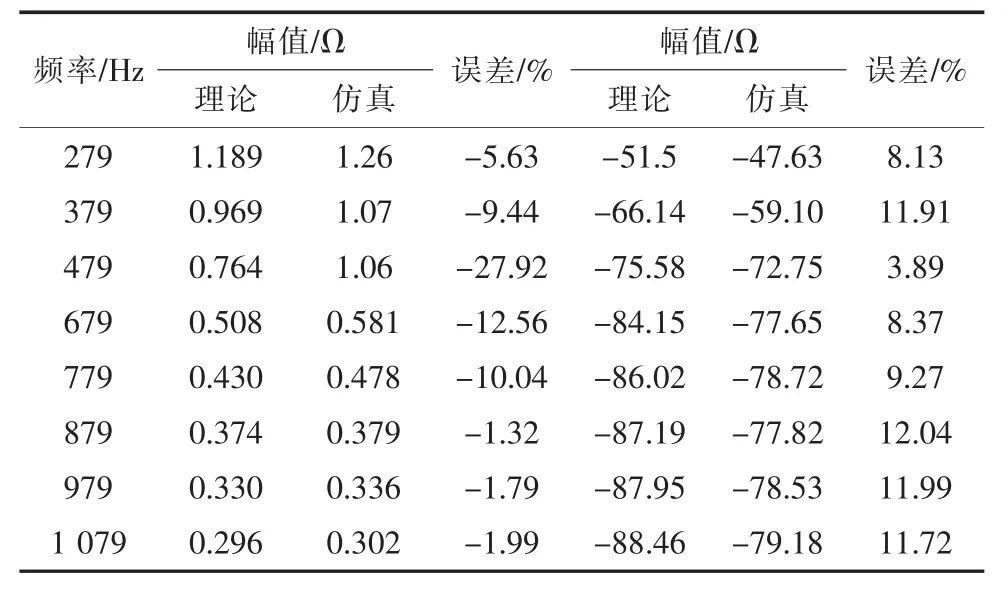
表4 網側換流器系統阻抗

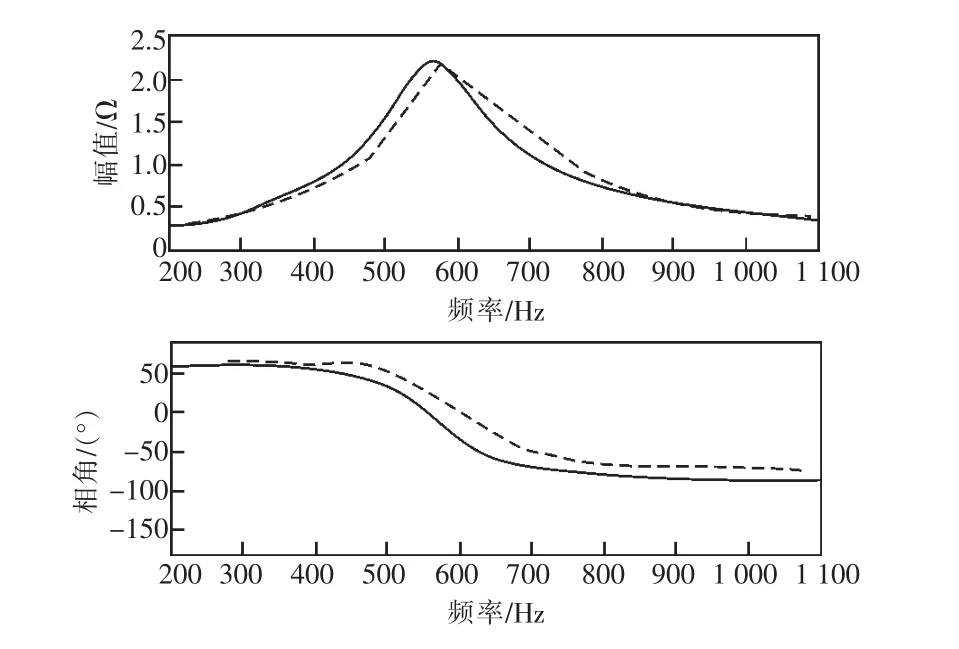
圖8 雙饋風機系統阻抗頻率特性

圖8和表5分別為雙饋風機系統的理論計算和掃頻法所得阻抗頻率特性對比。表5表明，在200～400 Hz和 800～1 100 Hz范圍內阻抗模值的理論計算結果與仿真結果誤差在10%內，相角誤差在20%內；而在400～800 Hz頻段內阻抗的相角誤差最大接近40%。

具體而言，雙饋風機系統總阻抗的誤差取決于阻抗小的子系統的誤差。在200～400 Hz頻段內，受控異步機系統阻抗模值明顯小于網側換流器系統阻抗，而其在該頻段誤差較小，因此系統總阻抗誤差較小；在400～800 Hz頻段內，網側換流器系統阻抗接近或小于受控異步機系統，而其在該頻段誤差較大，因此系統總阻抗誤差較大；在800～1 100 Hz頻段內，網側換流器系統阻抗明顯小于受控異步機系統，而其在該頻段誤差較小，因此系統總阻抗誤差較小。

表5 雙饋風機系統阻抗

結合圖8和表5可知，在200～500 Hz頻段內，雙饋風機系統阻抗呈現正電阻-電抗性質（該頻段受控異步機系統阻抗模值較小）；在500～1 100 Hz頻段內呈現正電阻-電容性質（該頻段網側換流器阻抗模值較小），且隨著頻率的增大，網側換流器系統阻抗模值先增大后減小。

綜上所述，本文研究的雙饋風機阻抗模型在200～400 Hz和 800～1 100 Hz頻段內有較高的準確性，在400～800 Hz頻段內理論模型準確性相對較低。目前可利用該阻抗模型實現雙饋風機系統在部分頻段振蕩風險的初步篩選和排查，未來需建立更加詳細的模型（考慮鎖相環、控制外環等）來實現對更多頻段振蕩風險的研究。

從振蕩風險的角度看，本例在900～1 100 Hz頻段雙饋風機系統呈現電容性質，可能與呈現電感性質的外電網構成等效諧振回路；同時，該頻段的雙饋風機阻抗角接近-90°且阻抗模值相對較小，即呈現弱阻尼性質，因此，在900～1 100 Hz頻段雙饋風機外送系統有一定的振蕩風險。

3 結論

本文基于傳遞函數的思想分析了高頻（大于200 Hz）擾動下雙饋風機系統的多頻率響應，并通過阻抗法和掃頻法分析了高頻段雙饋風機的振蕩風險。結論如下：

（1）當并網點存在頻率為fp的高頻擾動信號時，類似于次同步擾動，雙饋風機系統會向并網點輸出多個頻率為n1fp-n2f1的電流頻率響應，其中，fp和fp-2f1分量為主要的頻率響應分量，2fpf1和2fp-3f1分量幅值較小。

（2）雙饋風機系統向并網點輸出的電流頻率響應主要為來自網側換流器系統輸出的電流頻率響應。

（3）本文所建立的雙饋風機阻抗模型可對部分頻段的振蕩風險進行初步篩選和排查，未來需建立更加詳細的模型來實現對其他頻段振蕩風險的研究。