智能旋翼振動高階諧波控制方法

鄧旭東,胡和平,孟 微

(中國直升機設計研究所 旋翼動力學重點實驗室，江西 景德鎮 333001)

0 引言

直升機旋翼工作在復雜的非定常氣流環境中，前行側激波、后行側失速以及槳渦干擾等因素導致旋翼振動問題突出。振動載荷經旋翼軸傳遞引起機體振動，因此針對旋翼的控制是解決直升機振動問題的治本方法。智能旋翼采用智能材料作動器對槳葉整體或局部氣動面進行驅動，由此產生能夠抵消槳葉自身振動的附加氣動載荷。智能旋翼有主動扭轉槳葉(ATR)、主動格尼襟翼(AGF)以及主動后緣襟翼(ACF)等多種構型，其中ACF構型最具工程應用潛力，研究表明，采用恰當的控制方法，能有效抑制旋翼振動載荷。

針對智能旋翼振動控制方法，歐美國家開展了廣泛而深入的研究，大致可分為時域控制與頻率控制兩類。具有代表性的時域控制方法有基于線性系統的H∞方法[7-8]、基于狀態空間或傳遞函數模型的連續時間高階諧波控制方法(CTHHC)[4-6]以及神經網絡控制方法[3]。值得一提的是，歐直公司采用帶自抗擾能力的H∞控制器，分別在2006年與2009年對換裝ACF智能旋翼的EC145直升機進行了飛行驗證，結果表明施加主動控制后駕駛員座椅處的垂向振動降低到0.05g以下；MIT聯合波音公司采用基于傳遞函數模型的CTHHC方法，對帶后緣襟翼的SMART旋翼進行了閉環控制風洞試驗，槳轂垂向振動載荷最大降幅可達80%。以上兩項研究基本代表了歐洲與美國在該領域的標志性成果。頻域控制方面，以美國高校為主的研究人員針對基于準靜態傳遞矩陣的高階諧波控制開展了一系列理論與模型試驗研究[14-17]，結果表明在穩態飛行條件下，頻域方法對旋翼振動載荷有出色的控制效果。相比時域控制，頻率方法對計算資源要求更低，更易于實現。

在國內，智能旋翼振動控制研究起步較晚，主要進行了一系列理論跟蹤與半物理試驗工作。李春明[12]，夏品奇[13]分別采用神經網絡控制器與最優控制方法對ACF智能旋翼振動控制進行了理論分析。

本文以ACF智能旋翼為對象，結合廣義卡曼濾波識別算法與目標函數最優控制理論，構建了一種具有傳遞矩陣在線識別能力的頻域高階諧波控制方法。在此基礎上進行了閉環控制仿真，對參數影響與控制算法的魯棒性進行了分析，驗證了文中方法的有效性，同時得出了若干定性結論，可用于指導智能旋翼振動控制試驗。

1 高階諧波控制算法

對于N片槳葉的旋翼而言，槳轂振動載荷以頻率為NΩ的諧波量為主，由頻率為(N-1)Ω，NΩ以及(N+1)Ω的槳葉載荷集成得到(Ω為旋翼轉速)。因此ACF智能旋翼高階諧波控制的基本思路是通過對襟翼(N-1)Ω，NΩ以及(N+1)Ω諧波偏轉角的控制來抑制槳轂NΩ的振動載荷，控制流程如圖1。

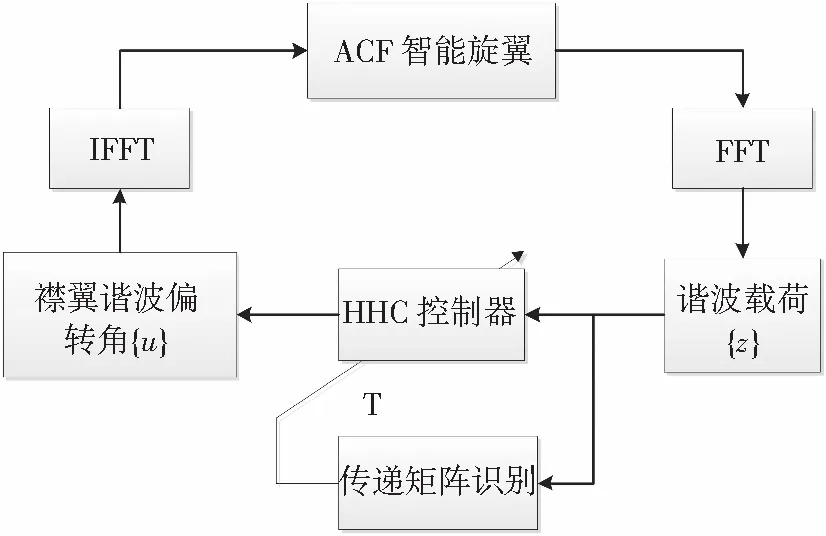
圖1 ACF智能旋翼高階諧波控制流程

其中傳遞矩陣識別與HHC控制算法是關鍵環節，其設計好壞直接影響振動載荷控制效果。u，z分別代表襟翼諧波偏轉角與旋翼諧波載荷的列向量，可表示為：

(1)

下標c，s分別代表余弦項和正弦項，N，N-1，N+1為頻率階次。考慮到槳轂載荷時域量FFT運算需要，通常令旋翼每旋轉整數倍圈更新一次u，傳遞矩陣T同步更新。

1.1 傳遞矩陣識別算法

ACF智能旋翼的傳遞矩陣模型建立在襟翼諧波偏轉角與槳轂諧波載荷之間的線性假設上，即：

(2)

其中下標k代表第k組樣本，一組樣本包含一個輸入列向量u和與之對應的輸出列向量z，可通過實測或計算得到。定義輸入、輸出樣本的增量矩陣為：

(3)

對于本文而言，Θ，Z，T分別為6×ns，12×ns，12×6矩陣，ns為識別所需的樣本數量。

傳遞矩陣T的識別采用廣義卡曼濾波方法，通過尋找T的最優解，使形如下式的性能指標函數JID達到極小值。

(4)

式中T*表示T的預估值；R，M分別為Z-TΘ，T-T*的協方差矩陣；下標i代表矩陣的第i行。當JID達到極小值時，有：

(5)

由式(4)、(5)可得：

TiΘRi-1ΘT-ZiRi-1ΘT-Ti*Mi-1+TiMi-1=0

由此可得到Ti的計算式：

(6)

將式(6)拓展到所有行：

(7)

T*可用上一步的T值代替，因此式(7)可視為傳遞矩陣的遞歸計算公式。

初始傳遞矩陣T0可通過預采集一定數量的樣本，利用數值微分法計算。矩陣R、M關系到識別精度，須預先設定，簡單起見可令R、M分別為對角陣，且各自的對角元素相等。通常廣義卡曼濾波識別效果同M與R對角元素之比直接相關，只需調整M/R即可對算法進行調諧。

1.2 振動控制算法

智能旋翼振動載荷高階諧波控制采用線性最優控制器，通過最小化目標函數Obj來給出相應的襟翼偏角輸入。

Obj=zkTWzzk+ukTWuuk+ΔukTWΔuΔuk

(8)

Wz，Wu，WΔu分別為輸出載荷、輸入偏角以及偏角增量所對應的權重矩陣，均為對角陣。當目標函數達到極小值時，?Obj/?uk=0，可得最優控制輸入為：

uk+1=(DkWΔu+DkTkTWzTk)uk-DkTkTWzzk

Dk=(TkTWzTk+WΔu+Wu)-1

(9)

下標k代表第k個控制步，每一步的控制輸入u與傳遞矩陣、權重矩陣以及上一步的輸入有關。

為調節控制量更新幅度，避免目標函數在控制過程中出現過大振蕩，引入修正系數α，即：

(10)

該控制算法性能依賴對權重矩陣與修正系數的調節，權重矩陣可采用如下設定方法：

(11)

式中系數βz，βu，βΔu用來設定向量z，u，Δu在目標函數中的占比，對角陣wz，wu，wΔu可調整向量中各元素之間的相對重要程度。對于ACF智能旋翼振動控制來講，主要目的是降低載荷向量z，但受限于襟翼運動能力，必須令u保持小角度，為保證相鄰兩步控制信號的連續性，還應使Δu盡量小。

2 算例與分析

以某4槳葉鉸接式ACF智能旋翼為例，分別從傳遞矩陣識別與振動載荷閉環控制仿真兩方面對本文所提出的高階諧波控制方法進行驗證。算例旋翼槳葉如圖2。

圖2 ACF智能旋翼槳葉

基本參數如表1。

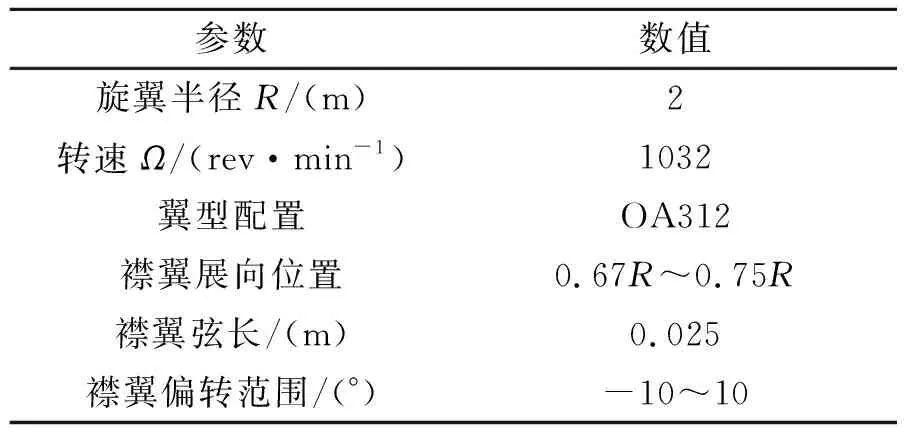
表1 算例旋翼基本參數

給定偏角輸入u，對應的旋翼振動載荷輸出z采用CAMRAD II計算得到，該軟件是一款成熟的直升機綜合分析軟件，已得到行業內的廣泛認可。所有計算均在旋翼前飛配平狀態下完成。

2.1 傳遞矩陣識別精度

令襟翼偏角輸入向量u的每個元素為-2.4°～2.4°之間的隨機量，在這種條件下計算70組輸入向量u對應的輸出z，并在每個輸入點處利用向前差分法計算z相對于u的雅克比矩陣TJ。

由于輸入、輸出數值上存在明顯的量級差異，為保證矩陣運算數值的穩定性，利用0偏角輸入下的載荷向量的絕對值abs(z0)作為輸出向量z的比例因子，輸入向量u的比例因子為2.4°，得到的70組輸入-輸出樣本用于傳遞矩陣識別，對應的雅克比矩陣可視為傳遞矩陣的確切值，定義識別誤差為：

(12)

令ns=6，M/R=0.001、0.01、0.05，樣本識別誤差分布如圖3。

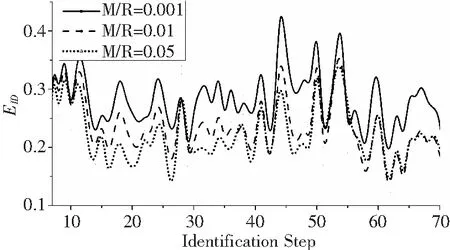
圖3 識別誤差分布(不同M/R)

由于識別運算需要ns個樣本，識別從第ns+1個樣本開始。圖中可見，識別誤差處于0.1～0.5之間，隨著M/R增大，誤差逐步減小。

令M/R=0.05，ns=2、6、10，樣本識別誤差分布如圖4。

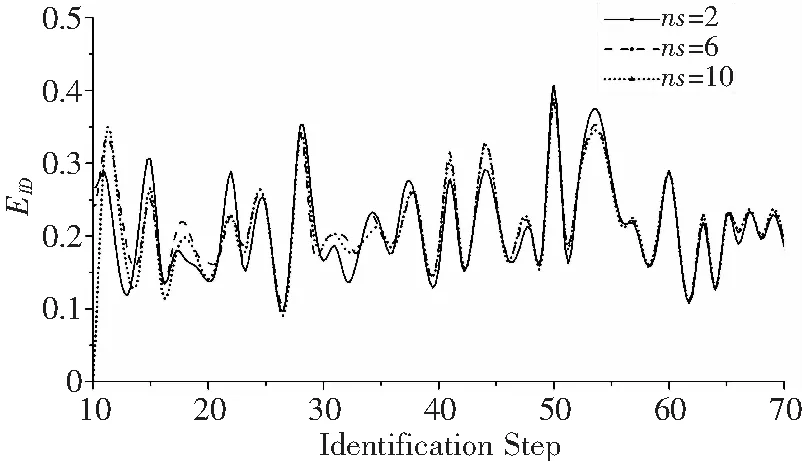
圖4 識別誤差分布(不同ns)

圖4表明樣本個數對識別精度影響不明顯，隨著識別步數增加，三條誤差曲線基本重合，因此僅增加樣本數量并不能提高識別精度。

2.2 振動載荷閉環控制仿真

2.2.1 特定狀態控制效果

采用帶傳遞矩陣在線識別的高階諧波方法對ACF智能旋翼進行振動載荷閉環控制仿真，旋翼工作狀態及算法參數如表2、表3所示。

表2 算例旋翼工作狀態

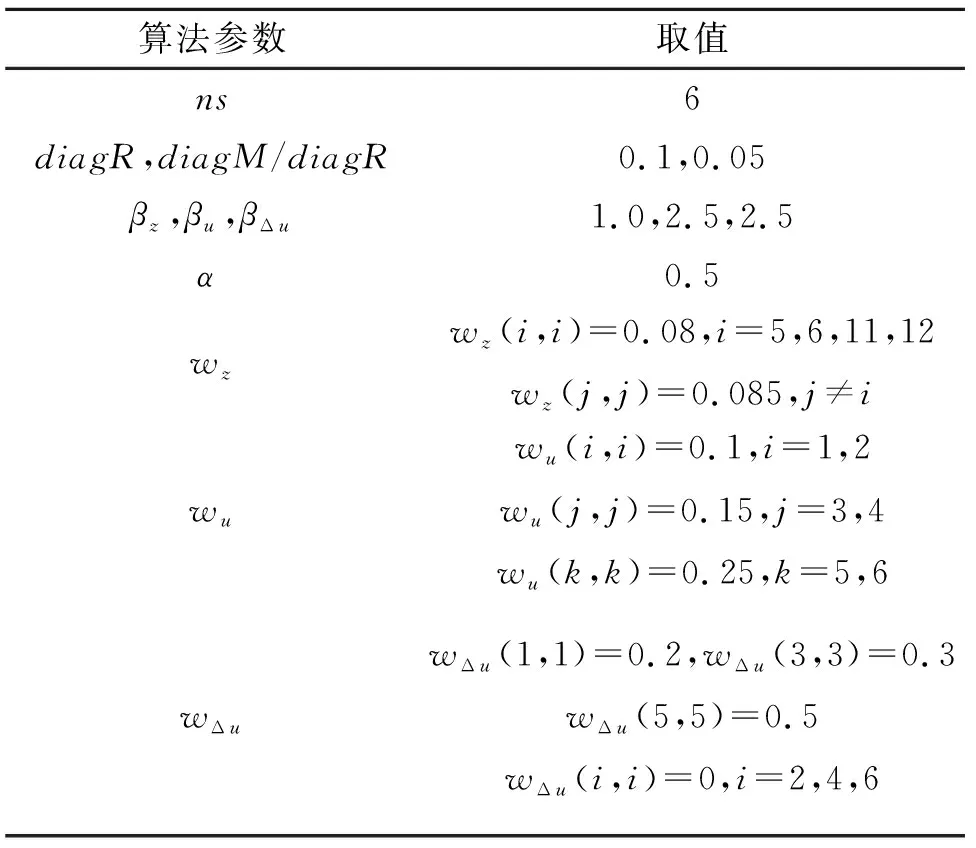
表3 控制算法參數

將基準狀態(0偏角輸入)下的振動載荷向量z0作為因子，定義目標函數的相對量：

Objr=Obj/(z0T·Wz·z0)

控制流程從0偏角輸入開始，目標函數的迭代過程如圖5。

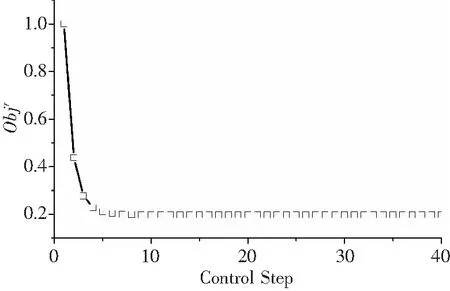
圖5 目標函數控制過程

由圖5可見，經過8次控制更新，目標函數約降低80%，隨后趨于平穩，實現最優控制。

圖6給出了算例旋翼基準狀態與最優控制狀態下，固定坐標系中4Ω無量綱槳轂載荷的對比。可見，三個方向上的旋翼振動載荷控制效果明顯，航向力F4x與側向力F4y的降幅超過40%；滾轉力矩M4x，俯仰力矩M4y以及垂向力F4z降幅在90%以上，扭轉力矩M4z的降幅也接近80%。

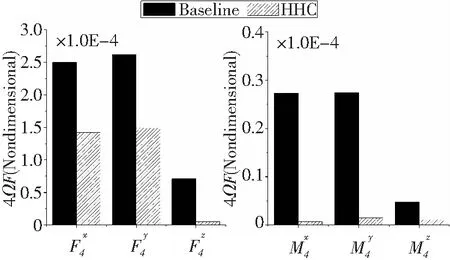
圖6 4Ω槳轂載荷控制效果

襟翼偏角向量u的更新過程如圖7所示， 6個分量在整個控制過程中均保持較小角度，連續性較好。

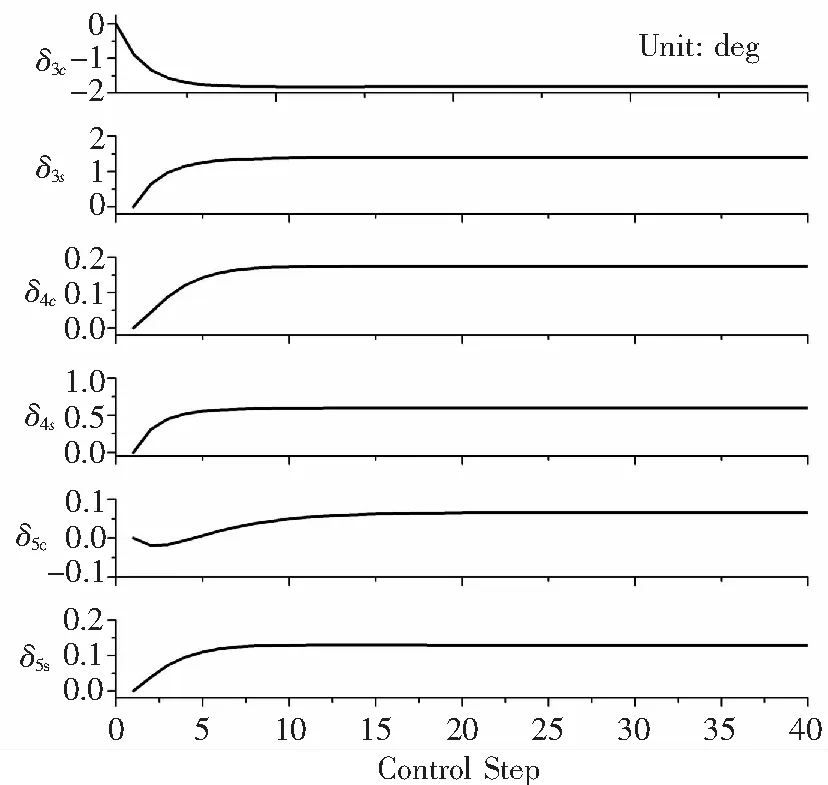
圖7 襟翼偏角輸入更新過程

2.2.2 權重矩陣影響

令前進比為μ=0.25，按照式(12)給出的權重矩陣設置方法，βz=1，分別令βu=βΔu=1、2、3 ，其他狀態與算法參數與表2、表3一致。目標函數迭代過程見圖8。

達到最優控制狀態后，無量綱4Ω槳轂載荷與襟翼偏轉角的時域量如圖9、圖10。

可見βu，βΔu越大，目標函數的降幅越小，控制器對旋翼振動載荷的控制能力越弱，這是由于襟翼偏角u及其增量Δu在目標函數中的比重升高，導致振動載荷z的比重降低，從而使其控制幅度減小。另一方面，βu，βΔu增大也降低了最優控制所需的襟翼偏角。

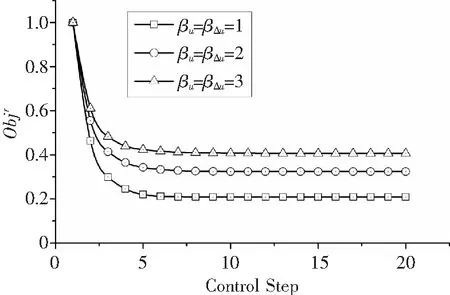
圖8 權重系數對目標函數的影響

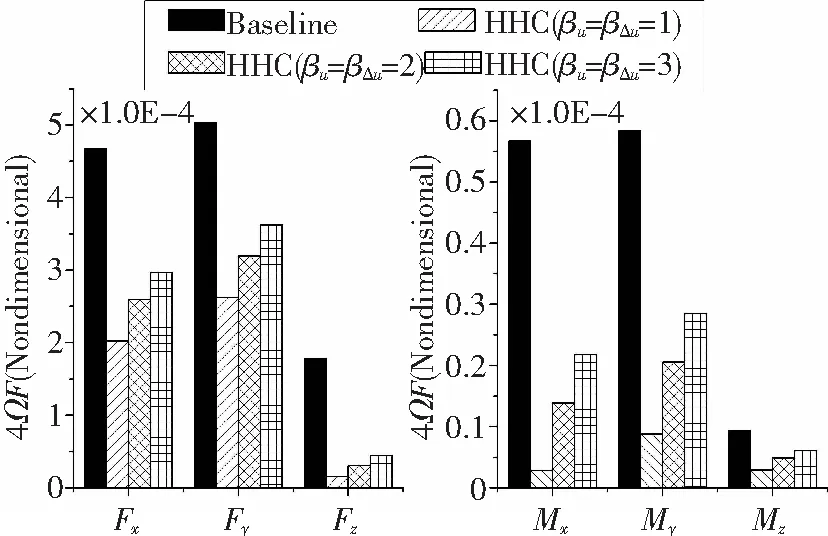
圖9 4Ω槳轂載荷控制效果對比

圖10 襟翼偏角對比

2.2.3 魯棒性驗證

為驗證控制器對旋翼工況變化的應對能力，采用表3給出的控制參數進行80步閉環仿真。控制以表2狀態為起始，并在進程中對旋翼工況依次進行如下改變：

1)第15步將μ提高到0.25；

2)第30步將CL/σ提高到0.08；

3)第45步恢復到初始狀態。

目標函數的變化歷程如圖11。

圖中可見，在第15、30、45控制步，目標函數有較大的波動，這是由于旋翼飛行狀態改變，導致輸入u到輸出z的傳遞關系發生較大變化，在線識別樣本中還包含上一狀態的u和z，無法準確識別T。隨著控制步增加，當前狀態的輸入、輸出數據逐漸填補進來，T的識別精度提高，目標函數得到了有效控制。第45步時旋翼恢復初始狀態，目標函數的控制水平隨即恢復。

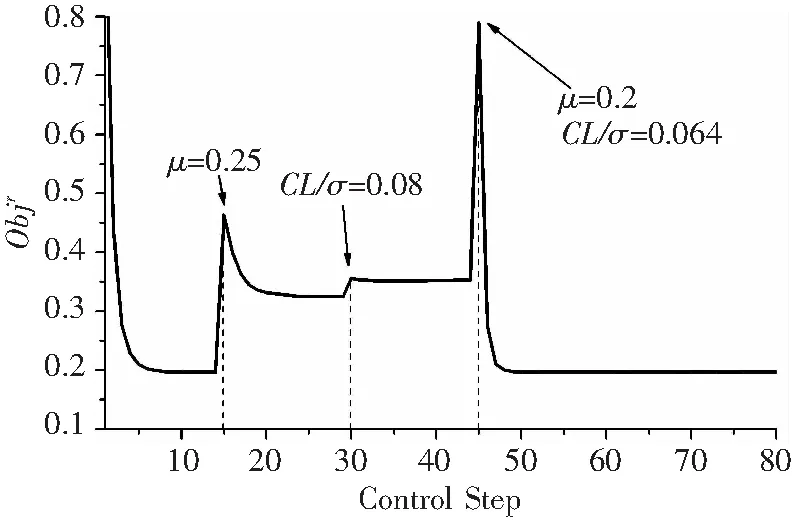
圖11 目標函數控制過程(變狀態)

為研究控制過程中4Ω旋翼振動載荷的變化規律，定義振動載荷相對量如下：

z0為對應狀態的基準載荷(0偏角輸入)，F4xr、F4yr、F4zr、M4xr、M4yr、M4zr的變化情況如圖12。

在各工況下重新達到最優控制狀態后，控制器對旋翼振動載荷的控制能力產生了不同程度的變化，其中槳轂力的控制能力變化不大，F4x與F4y的控制幅度均為40%左右，F4z的控制幅度保持在85%左右；槳轂力矩的控制能力變化明顯，初始狀態下M4x，M4y的控制幅度在90%以上，當前進比提高到0.25后，其控制幅度不到80%。M4z的控制幅度由初始狀態的80%變為60%。在工況改變的第15、30、45控制步，振動載荷各分量雖有波動，但總體上保持較低水平，只有垂向載荷F4z略微超過基準量。

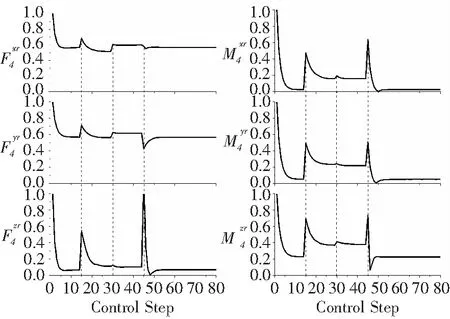
圖12 4Ω旋翼槳轂載荷相對量

3 結論

本文針對ACF智能旋翼，構建了一種帶傳遞矩陣在線識別的振動載荷高階諧波控制方法，通過閉環控制仿真對該方法的識別精度、控制效果、參數影響以及魯棒性等關鍵指標進行了分析凝練，形成結論如下：

1)對于周期性明顯的穩態飛行，采用頻域高階諧波控制能有效降低旋翼槳轂主通過頻率(NΩ)的振動載荷；

2)傳遞矩陣識別與控制量更新過程中涉及到大量矩陣求逆運算，為保持精度與數值穩定性，采用恰當的歸一化或無量綱處理是必要的；

3)ACF智能旋翼振動載荷控制的關鍵是在襟翼驅動能力范圍內實現載荷最小化，需要通過合理配置控制目標的權重矩陣來實現；

4)當閉環控制進程中旋翼工況發生變化，有可能導致某些方向的振動載荷產生較大的波動，而頻域控制需要一定的時間才能產生控制效果，因此在試驗過程中須對相關載荷進行實時監測，避免振動超限產生結構破壞。