基于分段線性坐標優化的退化壓縮感知水印檢測
陳 曉 鋒
(浙江大學寧波理工學院信息科學與工程學院 浙江 寧波 315000)
0 引 言
在無線移動信道(開放信道)上的多媒體數據傳輸面臨諸如版權保護和有限傳輸帶寬等安全問題。數字水印一般是隱含著著作權者的相關信息,用于版權歸屬設定,用戶對數據信息的處理需要首先對水印代碼進行處理。數字水印具有兩種屬性:永久嵌入屬性和易于讀取屬性,同時不能被人體視覺輕易感知到,并且嵌入的水印與原始信息之間不存在較為明顯的干擾。為了安全起見,嵌入水印不可被用戶輕易地刪除。雖然水印需要進行永久性標識,但相對而言不可對原始數據信息的訪問產生影響[1-2]。
當前的數字水印研究中已有很多成熟的算法。例如文獻[3]將圖像中常用的數字水印算法拓展到音視頻等多種格式數據文件中,采用的基本方式是利用擴頻方式進行數字水印的顯頻分量隱藏,問題是算法簡單的進行移植操作,其算法適應性相對較差。文獻[4]采用傅里葉算法對版權圖像的數字水印問題進行研究,將數字水印按照非遞增序列的形式進行嵌入,缺點是算法存在較大的失真問題,水印與原始圖像之間存在較大的干擾問題。文獻[5]采用圖像融合方式進行數字水印的嵌入,其可有效防止用戶的隨意復制,缺點是水印的嵌入分辨率較差。文獻[6]采用小波算法對數字水印問題進行研究,提出了具有可變換分辨率算法的數字水印檢測方法,缺點是算法的計算復雜度過高。文獻[7]設計了一種具有互補特性的數字水印檢測方法,算法的優點是不需要對圖像的原始數據信息進行參照,缺點是算法的水印檢測精度偏低。文獻[8]基于離散余弦變變換對數字水印算法的頻域檢測方案進行設計,可實現對水印圖像的信息進行調制,對于水印的魯棒攻擊性具有較強的抵抗能力。
上述算法在進行數字水印算法進行設計過程中雖然針對某一方面進行了針對性的設計,但是其優化解具有局限性,是一種局部極優的數字水印檢測方法。本文針對數字水印檢測算法設計了一種最優化計算模型,是一種多準則極值優化問題。近些年,在多準則極值優化問題研究中,已有很多成熟的計算方法,例如權值法、灰度值法、熵值法、均衡法等。這些方法對于多準則極值問題,具有一定的優化效果,但是問題是算法的主觀性過強,特別是算法的收斂性在理論上缺乏足夠的收斂依據。對此,本文利用分段線性坐標優化算法對多極值目標優化問題進行研究,實現對數字水印檢測的最優化實現。
從上述研究成果可知,以往的數字水印研究成果側重的是算法的實現,對于主機信號干擾HSI和衰減退化影響檢測器性能,考慮不是非常細致。為解決該問題,本文采用擴頻SS水印和壓縮感知CS進行算法融合,提出了一種優化問題模型,以最小化失真(包括CS重建和水印檢測)作為優化指標,采用檢測概率為特征的檢測可靠性約束,進行最優測量次數(提供帶寬)和嵌入強度的優化。
1 基于退化壓縮感知的擴頻水印檢測
在原始變換空間Ψ∈RN×N中,將長度為N的具有零均值和單位方差的獨立同分布(i.i.d)高斯模式P(∈RN)加到主機數據X∈RN×N中,如傅里葉、小波變換(這里使用)、離散余弦變換(DCT)等。SS水印可表示為:
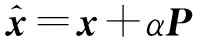
(1)
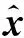

圖1 CS-SS水印圖像傳輸和水印檢測的系統模型
在檢測器側接收的CS測量y可表示為:

(2)
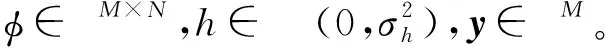
式(2)中的水印檢測可以被建模為兩個假設過程,H0(水印缺失)和H1(水印存在),如式(3)所示,均服從高斯分布。
(3)
式中:總干擾協方差矩陣是C可表示為:
C=E[yyH/H0]=E[(hφx+η)(hφx+η)H]=
(4)
式中:E(<φx,η>)=E(<η,φx>)=0;操作符〈p,q〉表示向量p和q的內積。基于φφH=IM,總干擾協方差矩陣C可改寫為:
(5)
基于式(5),在H0和H1情況下,y的概率密度函數(PDF)可表示為:
(6)
式中:det(·)表示矩陣的行列式。測試統計量t(y)可推導為:
(7)

(8)


(9)
(10)
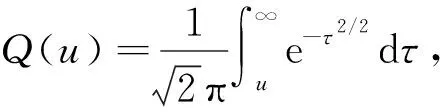
(11)
式中:對于已知的信道條件(退化函數)和給定的pfa,pd值取決于CS測量m的數目和水印強度α,即:
(12)
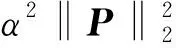
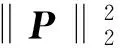
2 水印檢測可靠性優化
由于CS和水印檢測過程所導致的失真現象,可表示為如下模型:
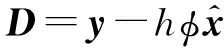
(13)
計算失真(e)的平均“L2”范數,具體計算過程如下:
(14)
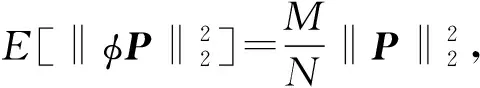
(15)
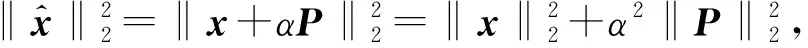
(16)
理論上,具有檢測可靠性約束的優化框架可以表述為:
(17)
(18)
(19)
式中:d2=z+α2+M2。將約束優化問題轉化為無約束優化問題,形式為:

(20)
當▽d2|M=0時,可得到d2的最小值,即d2的梯度。因此,可得:
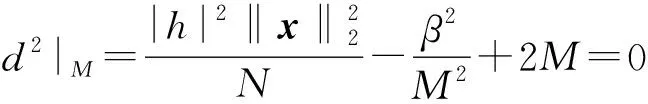
(21)
求解三次方程并放棄虛根,得到最優值M*的取值形式為:
M*= (b/2+((-a3/27+b/2)2-a6/729)1/2-
a3/27)1/3-a/3+a2/(9×(b/2+((b/2-
a3/27)2-a6/729)1/2-a3/27)1/3)
(22)
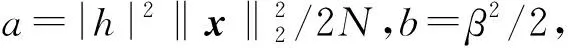
(23)
由此可得到目標函數(d2)的二階導數,計算形式如下:
(24)
式中:▽2d2|M是正的,這清楚地表明目標函數的值是最優M*值的最小值。因此,在給定的pfa=ξ中,pd的最佳值可以通過在式(13)中代入α*和M*來獲得。
3 分段線性坐標優化求解
3.1 算法描述
式(19)退化壓縮感知的擴頻水印檢測模型的求解,可采用坐標法進行優化。一般來說,對于給定的水印檢測模型網格頂點,主頂點位置上的擴頻水印檢測模型的值是最大的,而位于網匯聚點位置上的點最小,算法計算過程為:
Step1算法參數進行初始操作,設定t=1、k=1、i=1。
Step2設定分段線性坐標優化頂點νt=(i1,i2,i3),式中i1∪i2∪i3={1,2,3},參數i是分段線性坐標的圖標號。
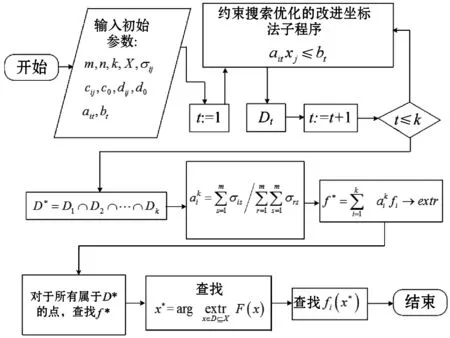
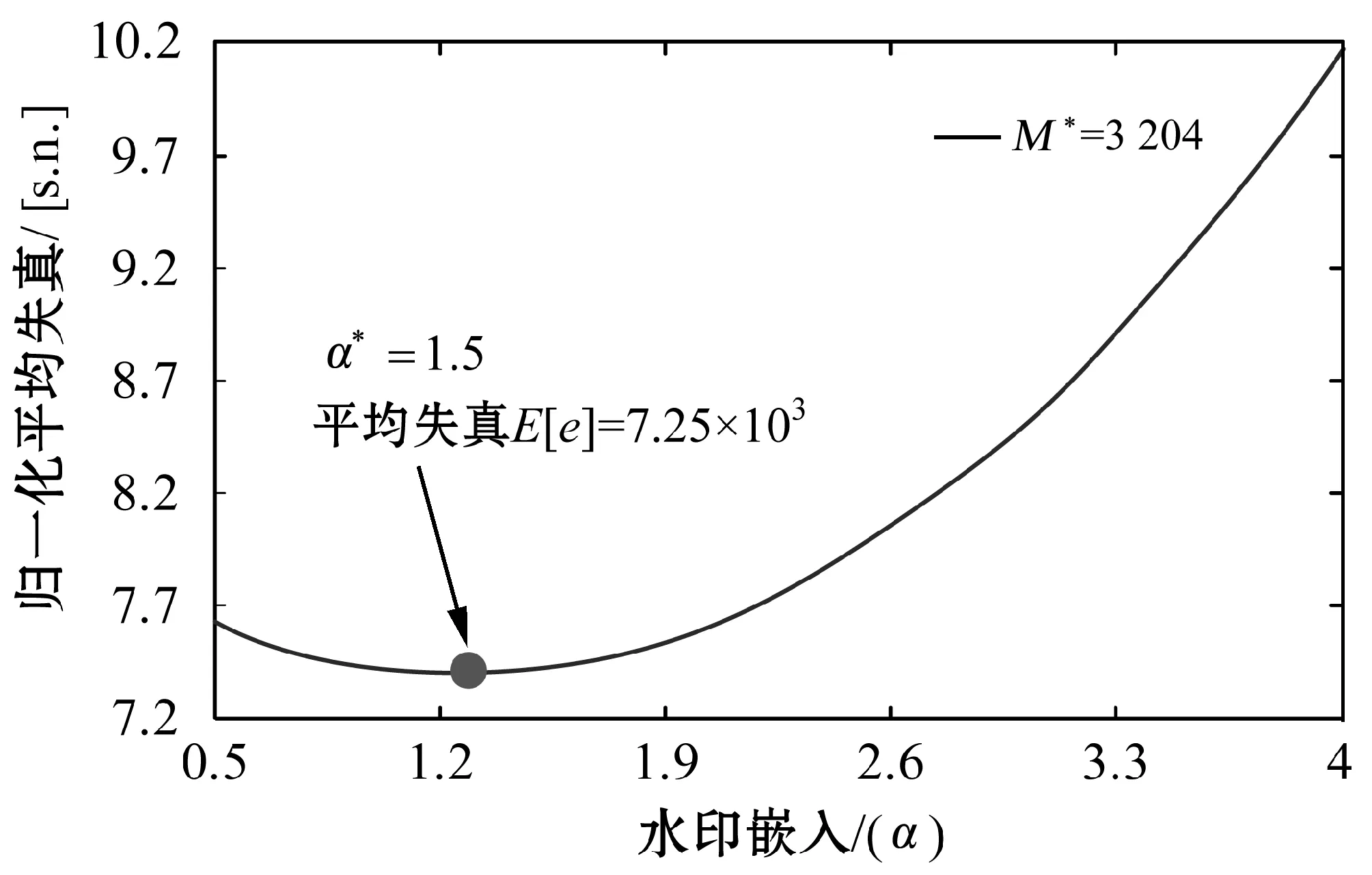
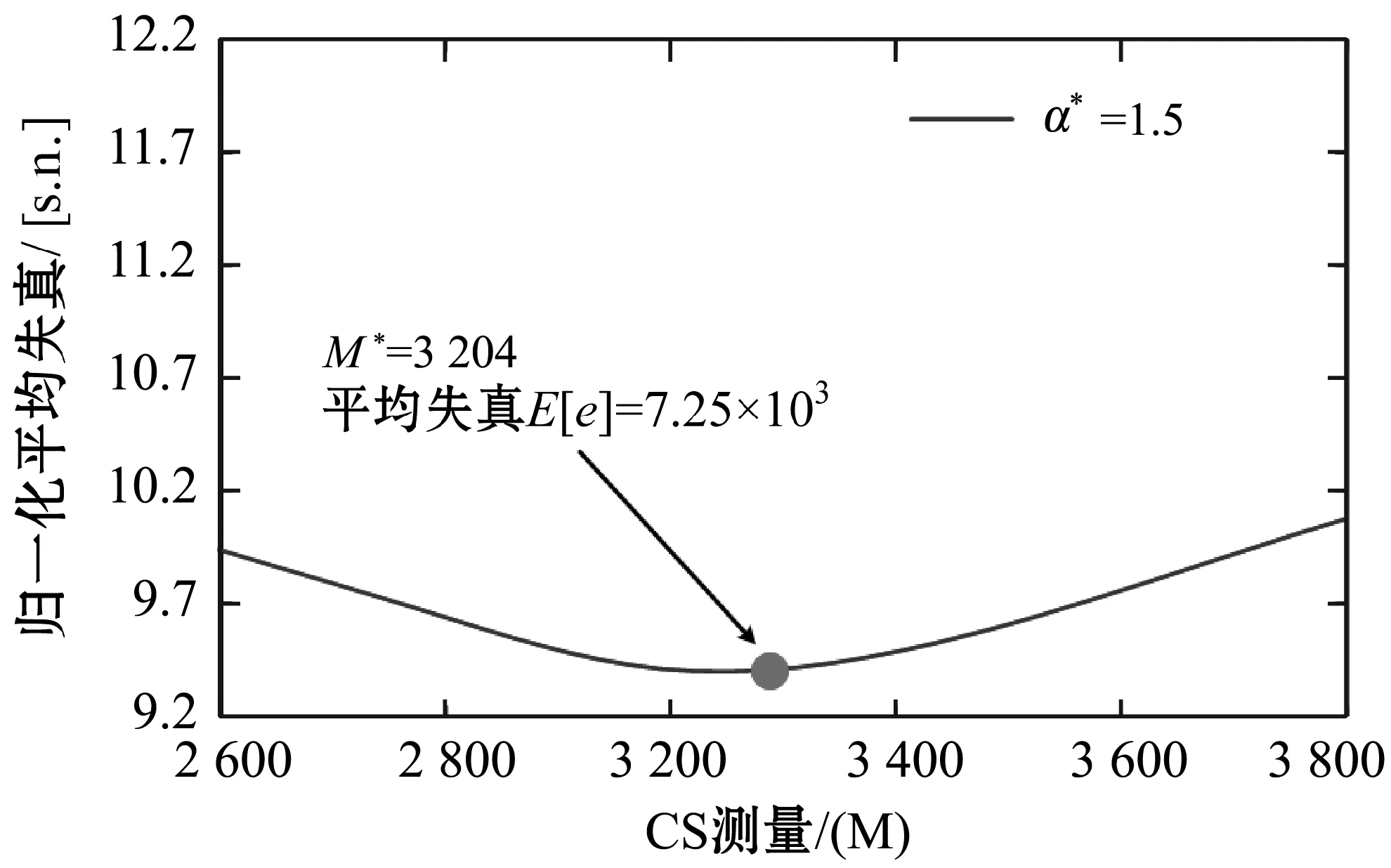
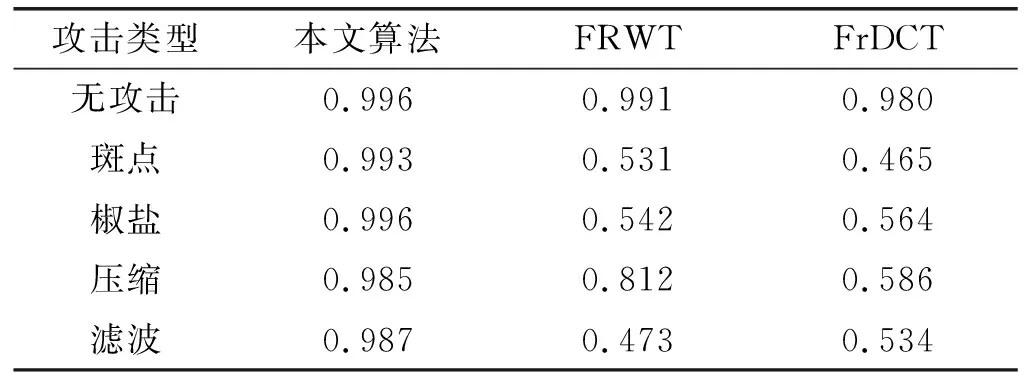
Step3查找xs=i,xs-1=max{Ns/xs},xs-2=max{Ns/(xs,xs-1)},…,x4=max{Ns/(xs,…,x5)}。采取升序方式對{Ns/(xs,xs-1…,x4)}進行序列的排列,且有j1 Step4查找xs=i,xs-1=min{Ns/xs},xs-2=min{Ns/(xs,xs-1)},…,x4=min{Ns/(xs,…,x5)}。采取升序方式對{Ns/(xs,xs-1,…,x4)}進行序列的排列,且有j1 Step5對于構建的坐標優化網絡,對f(p1)和f(pst1)進行對比,可對算法下一步的搜索方向進行確定,對于設定參數y*,若滿足f(p1)-y*≤y*-f(p1),按照從Sink節點到主頂點的逆向順序進行數字水印檢測模型的優化,并執行Step 6。若不滿足,則采取相反的方向進行算法目標函數的搜索優化,并執行Step 7。該算法過程的優點是算法的執行效率較高。 Step6采取降序方式對目標輸入xk排序,式中k∈Nk,jk>jk-1>…>j1。針對設定的序列jk?jk-1?…?j1進行坐標xk轉換,將產生k-1個坐標p2,p3,…,pk,得到算法的上層代碼,然后跳轉到Step 8。 Step7采取升序方式對xk排序,k∈Nk,jk>jk-1>…>j1。針對設定的序列jk?jk-1?…?j1進行坐標xk轉換,將產生k-1個坐標pst2,pst3,…,pstk,進而可得到算法的下層代碼。 Step8基于求解的坐標,形式如下:對于優化目標f(pn)=f(pn-1)-Δn-1,根據函數取值進行排列,式中μ(λ)為碼pn-1中jλ位置,Δn-1=(jn-jn-1)(cn-cμ(n-1))。 Step9按照順序對下列條件進行檢測: (a) 若滿足水印檢測模型條件f(pm)≥y*,則跳轉Step 10,繼續目標算法優化。 (b) 若滿足水印檢測模型條件f(pm) (c) 若滿足水印檢測模型條件f(pm) (d) 若滿足t+1≤6,則轉Step 2;否則,滿足該約束下對算法進行終結。 Step10假定k=k+1,若滿足k Step11采取降序方式對xk排序,k∈Nk,jk>jk-1>…>j1。針對設定的序列jk?jk-1?…?j1進行坐標xk轉換,可產生k-1個坐標q2,q3,…,qk。 Step12基于坐標f(qn)=f(qn-1)-δn-1,δn-1=(jn-jn-1)(cn-cμ(n-1)),對函數排列值進行查找,μ(λ)是函數目標排列碼qn-1中jλ所處的位置區域。 Step13若滿足水印檢測模型條件f(qn)≤y*,則保留坐標頂點qn,跳轉Step 10。 對于多準則極值優化問題,對分段線性坐標優化求解算法進行設計: Step1對于目標模型輸入,設定其參數約束以及目標準則。 Step2生成水印檢測模型的組合元素。 Step3對于設定的約束k,基于改進坐標法對組合問題排列進行求解,可得到可行解集D*子集Di?X,i∈Nk。 Step4查找可行解D*=D1∩D2∩…∩Dk。 Step7對于點x∈D*位置進行函數f*值優化求解。 Step8對選取優化方向與Step 7所得數值進行對比,可得目標極值。 Step9對數字水印檢測模型的線性分式函數近求解。終結算法。 數字水印檢測模型的線性分式函數求解算法如圖2所示。 圖2 算法流程圖 實驗平臺:CPU i7-6500k 2.9 GHz,RAM 6 GB DDR4 2 400 MHz,系統為Win10旗艦,仿真軟件是MATLAB 2013b。選擇lena(萊娜)測試圖作為載體,Punjabi Logo作為水印,大小是M/3×N/3,圖像大小M×N=300×300。 這里設定的最佳參數主要是M*和α。利用Daubechies 9/7小波對256×256,8位/像素萊娜圖像(圖3(a))進行小波變換,將其分解為3級。假定小波系數的分布遵循GSM模型。水印檢測在方差小于閾值(1 000)的小波系數集合中。圖3(b)和圖3(c)分別給出用于78%的CS測量的水印圖像(PSNR=44.86 dB)和重建水印圖像(PSNR=32.96 dB)。利用CS測量的最佳值(M*=3 204),水印檢測強度(α*=1.5),可獲得具有零均值和方差0.7(h~CN(0,0.7))的復正態分布的瑞利衰落的水印檢測強度,而具有零均值和方差0.25的加性高斯噪聲(η~N(0,0.25))。 (a) 原始圖像 (b) 水印圖像 (c) 重構圖像圖3 實驗圖像 最佳參數M*和α的選取結果如圖4所示。 (a) 最優CS測量中的歸一化平均誤差與水印檢測強度(M*=3 204) (b) 歸一化平均誤差與CS測量在最佳水印檢測 強度上的比較(α*=1.5)圖4 測量結果對比 圖5 檢測概率對比 根據圖5結果可知,文獻[6]中的工作提出了一種魯棒的和分層的CS水印方案,其中水印的檢測可以在加密域或解密域中完成。本文算法相對于文獻[6]算法可實現顯著性能改進,約提升5.43%,因為本文采用的是最優檢測器設計。 為了驗證所提出的算法對于數字水印檢測過程中高頻分量影響的魯棒性,利用噪聲點對數字水印的嵌入過程進行模擬攻擊測試。選取的模擬攻擊噪聲主要有4種類型,分別是:斑點、椒鹽、壓縮和濾波等。其中:斑點噪聲的參數設置是mean=0,var=0.4;椒鹽噪聲的參數設置是var=0.4;壓縮攻擊過程的參數設置是Q=20;濾波攻擊過程的參數設置是[50,50]。對比算法選取FrWT和FrDCT兩種算法,分別見參考文獻[14-15]。實驗結果如圖6所示。 (a) 斑點攻擊 (b) 椒鹽攻擊 (c) 壓縮攻擊 (d) 濾波攻擊圖6 水印檢測算法性能對比 根據圖6的實驗結果可知,當采用lena圖像作為水印圖像時,圖6(a)、(b)以及(d)所示的椒鹽攻擊、斑點攻擊、濾波攻擊中,其類似于真實環境下的人造邊緣攻擊,是一種高頻的攻擊形式。實驗結果顯示,本文算法相對于文獻[14-15]可得到更加清晰的數字水印圖像,而文獻[14-15]兩種算法檢測到水印圖像存在非常明顯的高頻干擾,水印圖像不夠清晰,甚至無法進行準確的識別。在壓縮攻擊算法中,本文算法可以提取到清晰的水印,而FrWT算法提取的水印雖可識別,但是存在一定的模糊性,效果相對較差,FrDCT提取到的水印難以識別。 圖6實驗對比結果通過視覺方式對算法的水印檢測性能進行了驗證和對比,是一種定性分析結果。下面從定量角度對算法的水印檢測性能進行實驗驗證和對比,結果如表1所示。 表1 水印檢測性能量化對比 根據表1實驗結果可知,對于選取的集中攻擊類型,本文算法對于水印檢測的效果均要優于選取的文獻[14-15]兩種對比算法。根據以上實驗結果,本文所提算法在水印圖像檢測過程中相對于選取的文獻[14-15]兩種對比算法具有更高的抗攻擊能力和魯棒性。 本文提出一種基于搜索優化改進坐標法的退化壓縮感知水印檢測算法,以最小化失真作為優化指標,采用檢測概率為特征的檢測可靠性約束,進行最優測量次數(提供帶寬)和嵌入強度的優化。采用圖論處理方式進行坐標搜索算法的優化過程改進,獲得一組能夠符合約束限制的解集,實現對水印檢測算法性能的提升。存在的問題:1) 本文算法側重于過程的實現和實驗的驗證,在理論分析方面稍顯不足;2) 算法在實驗室條件下得到了很好的驗證,對于真實應用場景的效果,有待于進一步驗證。這兩方面是今后研究的重點。3.2 改進坐標優化算法
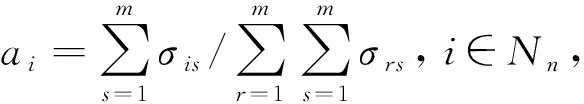
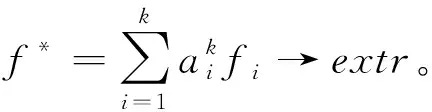
4 實驗結果
4.1 水印檢測:求最佳參數設置



4.2 抵御攻擊測試




5 結 語

