帶有冗余度的新型連續地月載荷轉移系統動力學與能量分析

陳振朋，李廣華，管瑋喬

(空軍航空大學航空作戰勤務學院，長春130022)

0 引言

隨著對月球、火星等初期探索的逐步開展以及相應關鍵技術的掌握,月球、火星等太空基地的建立將成為深空探索的必然趨勢。屆時,連續型、大批量地進行地月、地火太空人員和物資的轉移將成為必然。因此,針對低成本、可重復使用、高效率的星際轉移方式或運輸工具的研究,將是人們不得不考慮的一大技術難題。基于動量交換的連續地月載荷轉移系統(Motorized Momentum Exchange Tether,MMET)作為一種具有上述優點的地月轉移系統,將成為一種可能的地月物資運輸方式。

MMET概念首次由英國格拉斯哥大學的Cartmell教授提出[1],這種連續地月載荷轉移系統(Continuous Cislunar Payload Transfer System,CCPTS)由運行于地球某橢圓軌道的駐地載荷轉移子系統(Earth Motorized Momentum Exchange Tether,EMMET)和運行于月球某橢圓軌道的駐月載荷轉移子系統(Lunar Motorized Momentum Exchange Tether,LMMET)2部分組成。2套系統的結構相同,均由位于系統質心處的母星、2根等長的細繩和2套相同的抓捕機構組成。2套系統的工作原理相似,在驅動力矩的作用下,通過調整2個載荷的動量,可以同時實現載荷的升軌和降軌。

針對MMET系統的動力學研究,已經積累了大量的理論研究成果。Ziegler和Cartmell將細繩看作剛性桿,對該系統的動力學特性進行了初步研究[2-4]。研究結果表明,驅動力矩的存在會對母星的軌道參數產生微小的影響。哈爾濱工業大學的陽勇[5-8]博士在考慮細繩長度偏差、載荷質量偏差的前提下,建立了系統二維誤差動力學模型。細繩長度偏差和載荷質量偏差會對系統廣義坐標和廣義速度產生相似的影響,隨著細繩長度偏差增大,廣義坐標和廣義速度偏差量的最大值呈現出了線性增加趨勢。在此研究基礎上,他又從能量的角度對比分析了CCPTS系統與傳統脈沖變軌方式在載荷轉移過程中的能量消耗問題[9]。結果表明,在轉移相同質量的載荷時,CCPTS將消耗更少的能量。

以上研究內容主要集中于CCPTS的建模和能量分析方面,沒有考慮到系統的可靠性和轉移效率。由于CCPTS需要在復雜的太空環境中長期在軌運行,如果其中1根細繩被太空垃圾剪斷,整個系統就會失去運載能力,可靠性低。同時,如果第1次抓捕載荷失敗,系統需要經過很長時間的調整才能完成載荷的第2次抓捕,效率也比較低。考慮到轉移效率,Cartmell[10]教授曾提出過階梯式多級入軌系統的概念,而陽勇[9]則提出了具有6根細繩的 “摩天輪”式的載荷轉移系統。這2種系統的復雜度都很高,細繩展開過程有很大難度,可靠性低。鑒于此,本文從提高可靠性和轉移效率的角度出發,同時綜合考慮系統的復雜性,設計了帶有1套冗余抓捕機構的新型連續地月載荷轉移系統(New Continuous Cislunar Payload Transfer System,N-CCPTS)。本文首先采用Lagrange方法建立了NCCPTS的二維剛性動力學模型,計算分析了冗余抓捕機構對系統參數變化規律的影響,然后研究了在轉移相同質量載荷時,Hohmann變軌、CCPTS和NCCPTS 3種轉移方式所需的能量問題。研究結果表明,冗余抓捕機構的存在對系統參數變化規律的影響是小量；在轉移相同質量的載荷時,N-CCPTS所需的能量仍然小于Hohmann變軌；當橢圓軌道遠地點半徑足夠大時,N-CCPTS相比CCPTS更加節省能量,且轉移效率是CCPTS的2倍。該系統可以為高效率的連續地月物資轉移提供一種更加可行的方案。

1 N-CCPTS概念

N-CCPTS有2套相同的抓捕機構,并且在抓捕機構之間用加強繩進行了連接,以保持其空間構型。在軌運行過程中如遇某根細繩被剪斷的情況,可以主動剪斷與之對稱的細繩,從而保持結構的對稱性,使系統能夠繼續正常工作。N-CCPTS的結構如圖1所示。

與CCPTS相比,N-CCPTS只增加了1套抓捕機構,從而在不增加太多復雜度的前提下提高了系統的可靠性。同時,如果由于某些誤差的原因,工作中的抓捕機構沒能捕獲到載荷,冗余抓捕機構可以繼續捕獲載荷,從而提高系統的載荷轉移效率。

2 N-CCPTS二維剛性動力學模型

2.1 坐標系定義

(2)體軸坐標系OMxbybzb

OMxb是由低軌的抓捕機構、載荷組合體指向高軌的抓捕機構、載荷組合體,OMyb位于軌道面內且垂直于OMxb,OMzb與OMxb、OMyb構成右手坐標系。

2.2 動力學建模

在對N-CCPTS的初期動力學研究中,為了簡化計算,暫時不考慮系繩旋轉面與軌道面的夾角,忽略系繩的彎曲變形和軸向彈性變形,同時忽略第三體引力以及地球扁率等擾動因素的影響,建立NCCPTS在相對慣性坐標系(即軌道面坐標系)中的二維剛性動力學模型。假設在某一時刻,系統質心OM、抓捕機構E2／E4、抓捕機構和載荷組合體P1／P3、各細繩上距離質心距離為x的質量微元dm的位置如圖2所示,并且忽略加強繩的質量(相比于細繩,加強繩更細,質量更小),則有:

其中,ui＝αi＋θ,αi＝α＋(i－1)π／2(i＝1,2,3,4)。 對以上各式求導可得速度矢量的表達式:

由于系統做平面運動,由動能的定義可知,系統的動能可以表示為平動動能和轉動動能之和。其中,平動動能為:

式中,M＝MM＋2MP＋2ME＋4MT表示NCCPTS的總質量；MM、MP、ME及MT(MT＝ρAL)分別表示母星、載荷和抓捕機構組合體、抓捕機構及剛性桿的質量。

假設N-CCPTS的各部分均為圓柱體,且各部分的幾何尺寸如圖3所示,則系統的轉動動能為:

聯立式(9)和式(10),可得系統的總動能為:

假設細繩為剛性桿,因此不用考慮其彈性勢能,則勢能只由重力產生。由引力場中的勢能定義,可得系統各部分的勢能為:

在滿足動力學研究的前提下,為了簡化分析,對式(14)～式(16)采用Taylor多項式展開,并略去x／R、x／L二次以上的項,從而得到各部分勢能函數的近似表達式為:

結合以上各式,得到N-CCPTS的勢能為:

結合式(12)和式(20),可得系統的Lagrange函數為:

選擇(RM,θ,α)作為系統的廣義坐標,相應的廣義力為(0,0,τ)。其中,τ表示作用在母星上的驅動力矩,則N-CCPTS的動力學微分方程為:

2.3 能量方程

文獻[9]已經證明,無論是圓軌道還是橢圓軌道,在轉移相同質量的載荷時,CCPTS所需的能量均小于傳統Hohmann轉移方式所需的能量。由于航天器的運行軌道基本都是橢圓軌道,因此,本文以橢圓軌道轉移為例,對比分析在轉移相同質量的載荷時,3種載荷轉移方式(Hohmann變軌、CCPTS、N-CCPTS)能量消耗的區別。

假設停泊軌道為橢圓軌道,近地點半徑為rp－L,遠地點半徑為ra,此時,N-CCPTS所需的能量為:

式中,2是橢圓軌道實現載荷轉移所需的角速度。

3 動力學與能量分析

仿真參數如表1所示,各廣義坐標初值為:

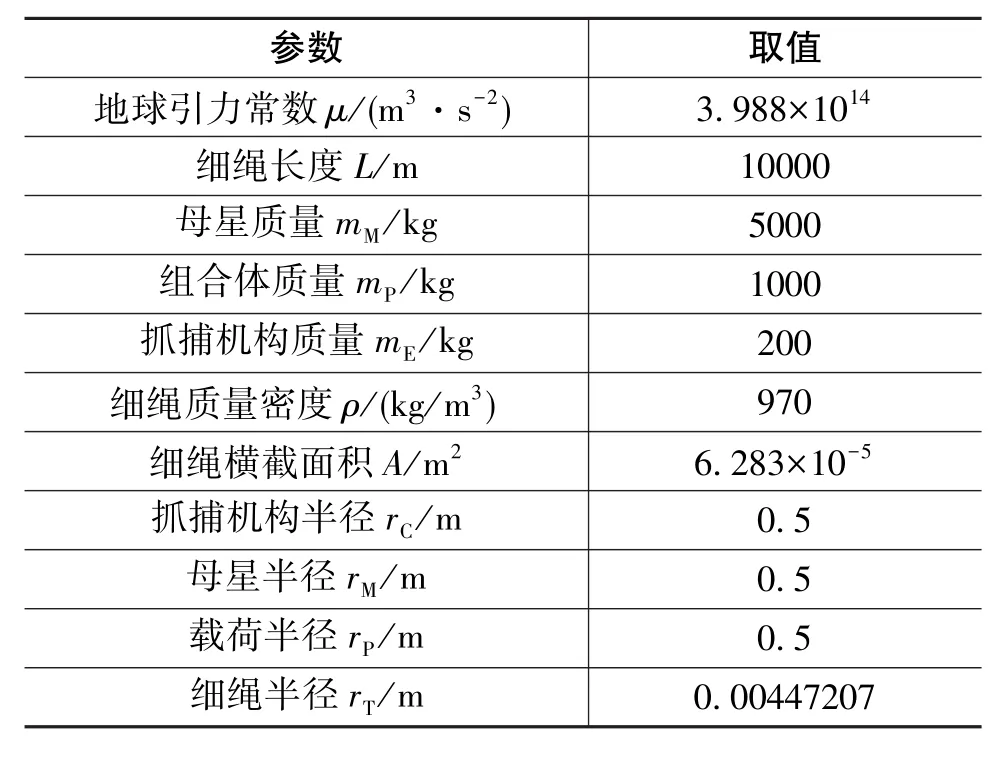
表1 N-CCPTS參數Table 1 Parameters of N-CCPTS

3.1 動力學分析結果

N-CCPTS系統的動力學方程與文獻[9]中CCPTS系統的動力學方程相比,兩者的差別主要在于M的動力學微分方程,定義:

其中,

無論α如何變化,3sin2α－1是一個有界的函數,將RM(0)以及表1的參數帶入Κ的表達式,計算結果約為4.66×10－7,可視為一個無窮小的數,因此Δ也可視為無窮小的數,可見該項對動力學方程的影響可忽略不計,冗余抓捕機構的存在對系統參數(軌道和姿態)變化規律的影響是小量,可以忽略不計。圖4所示的仿真結果表明,系統質心矢徑RM仍然隨時間做周期變化,相比于CCPTS,其在近地點和遠地點會有細微差別,但變化規律沒有改變。同理可以證明θ和α的變化規律,圖5和圖6分別給出了兩者的變化關系,與CCPTS相同。

3.2 能量分析結果

假設軌道近地點半徑滿足rp＝6.726×106m,3種載荷轉移方式所消耗的能量隨軌道遠地點半徑ra的變化關系如圖7所示。

由圖7可知,在轉移相同質量的載荷時,NCCPTS消耗的能量多于CCPTS,這是因為冗余抓捕機構的存在使得系統的轉動慣量增加,進而使得能量消耗增加,但其仍然少于Hohmann變軌。此外,3種載荷轉移方式消耗的能量都隨著軌道半徑的增加而減小,這說明增加軌道半徑可以減小能量的消耗。

為了反映CCPTS與N-CCPTS在能量消耗方面的細微差別,定義:

圖8給出了在橢圓軌道中,ΔE隨軌道遠地點半徑的變化關系。經過計算,當軌道遠地點半徑大于2.75×108m時,N-CCPTS所消耗的能量少于CCPTS。這表明,當軌道半徑足夠大時,N-CCPTS是更加節省能量的方案。

4 結論

1)冗余抓捕機構的存在提高了系統的可靠性和轉移效率；

2)相比于CCPTS,冗余抓捕機構的存在對動力學參數變化規律的影響是小量；

3)當初始軌道是橢圓軌道時,當軌道遠地點半徑足夠大時,在轉移相同質量的載荷時,NCCPTS方式更為節省能量。

綜上所述,相比于CCPTS,N-CCPTS是一種適用于連續地月物資轉移的更加可靠、高效和可行的方案。