基于無線傳感器網絡的不確定系統魯棒融合Kalman濾波

池小波，王 艷，賈新春

（山西大學 數學科學學院，太原 030006）

多傳感器信息融合估計在目標跟蹤和信號處理中起著重要作用，其基本原理是融合測量數據或局部估計，以獲得較高精度的最優估計[1]。基于Kalman濾波的融合估計通常包括集中式和分布式2種。與集中式融合相比，分布式融合需要較少的計算和通信負擔，并且更加靈活可靠。

基于Kalman濾波的網絡化融合估計問題受到了相關領域學者的廣泛關注[2]。針對網絡誘導特征，文獻[2-4]或者僅考慮對象到傳感器間存在時延的情形，均未考慮傳感器到估計器間存在的網絡誘導特征，或者只是考慮單一特征，因此帶有多種網絡誘導特征的分布式估計問題的研究仍然面臨眾多挑戰[5]。

由于建模誤差、網絡時延和丟包的影響使得系統中可能存在不確定性，而傳統的Kalman濾波方法需要已知模型參數和噪聲統計量，因此傳統的濾波方法不適用于帶有上述不確定性的問題，需要提出新的Kalman濾波方法來改進估計性能。

近年來，魯棒Kalman濾波受到極大的關注[3，6]，然而現有的魯棒Kalman濾波器僅適用于具有噪聲方差不確定性的系統，很少考慮模型參數不確定性[7]，且數究工作大多僅限于單傳感器系統的魯棒Kalman濾波設計。針對多傳感器系統的魯棒融合估計問題，特別是同時考慮模型不確定性、網絡誘導時延和丟包特征共存的分布式融合估計問題還很少被考慮[8]。考慮到相關分布式估計研究現狀，文中在分布式融合框架下，對帶有上述特征的多傳感器融合估計問題開展研究。針對帶有網絡誘導時延和丟包的無線傳感器網絡和不確定模型，文中提出基于魯棒Kalman濾波的分布式融合估計方法。

1 問題描述

1.1 分布式網絡化融合框架

考慮如下一類帶有不確定參數的線性動態系統

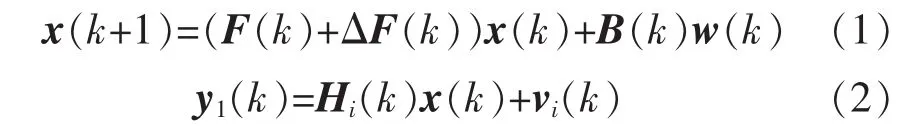
其中

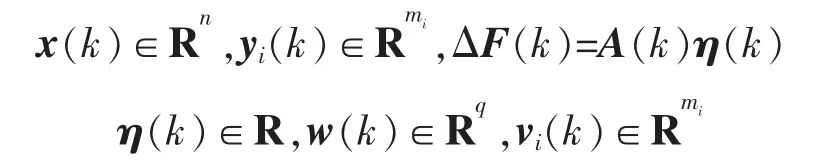
式中：x（k）為狀態向量；yi（k）為第個傳感器的量測輸出；ΔF（k）為狀態依賴的系統參數不確定項；F（k），A（k），B（k）和 Hi（k）為適當維數時變矩陣；η（k）為零均值高斯白噪聲；w（k）為系統的過程干擾，v（k）為量測噪音，且 w（k）和 vi（k）均服從零均值高斯分布，其協方差矩陣分別為 Q（k）和 Ri（k），i=1，2，…，N。

假設 w（k）和 vi（k）為相互獨立的高斯白噪聲，并滿足以下統計特性：

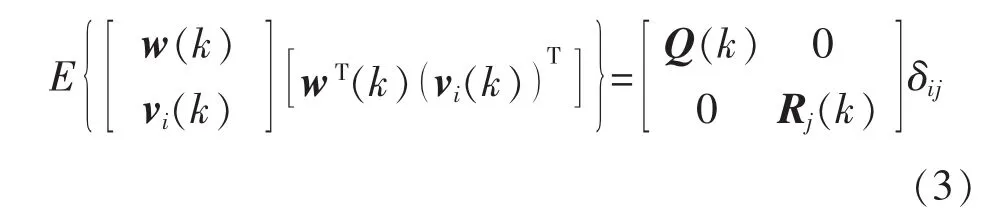
其中，當 i=j（其中 i，j=1，2，…，N），δij=1，反之則為0。 假設 x0，w（k）和 vi（k）相互獨立，滿足 E（x（0））=x0，Var（x（0））=P0。

假設，在無線通訊網絡中部署N個傳感器以監測不確定系統。分布式融合估計框架如圖1所示，框架中每個傳感器分別采樣系統（1）的量測輸出。采樣數據通過網絡傳輸時考慮網絡誘導時延和丟包等現象，局部估計器使用接收到的信息設計局部估計信號，最后通過CI融合方法得到比局部估計精度更高的融合估計。

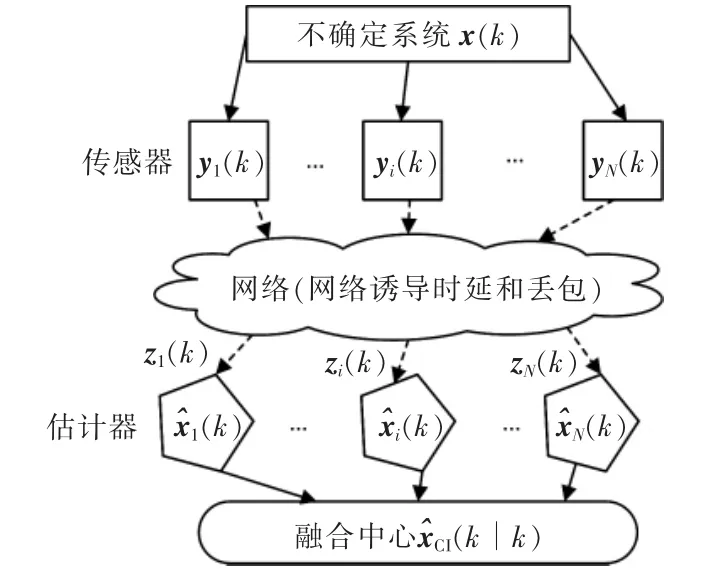
圖1 分布式融合估計框架Fig.1 Distributed fusion estimation framework

1.2 傳輸時延和丟包

由于網絡中存在時延和數據丟包，估計器收到來自傳感器的采樣數據滯后于最新的量測值，則k時刻估計器i收到的量測值為zi（k），即

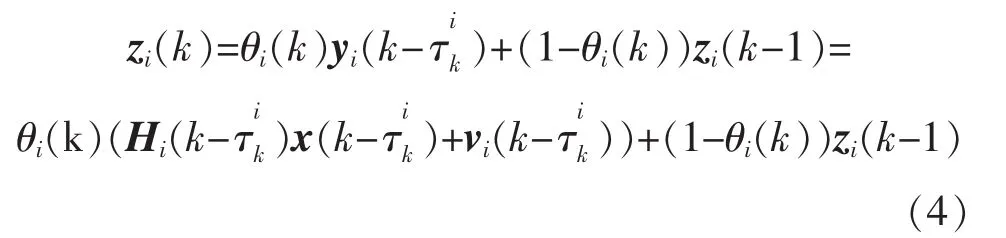
其中

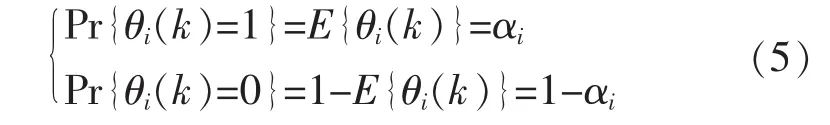
其中，不同的傳感器通過網絡傳輸時具有不同的丟包率，αi為傳感器i通過網絡的到達率，則有[4]

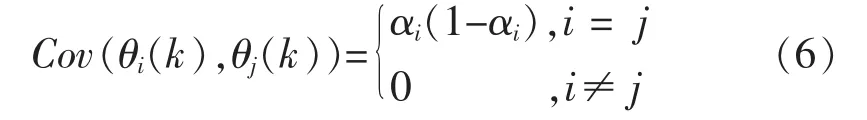
本文目的是同時考慮網絡誘導時延和丟包情形下，研究不確定性系統的最優融合估計問題。首先，基于革新序列（符號定義見文中式（12）），確定局部Kalman濾波增益Ki（k），使得誤差協方差矩陣 Pi（k∣k）最小（i=1，2，…，N），然后給出融合估計和PCI（k∣k）。

2 網絡化魯棒Kalman濾波的局部估計

值，即線性最小均方誤差估計x贊i（k∣k）可定義為

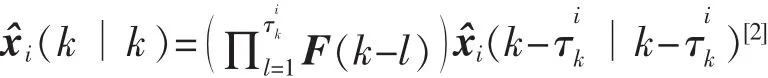
預測誤差和濾波誤差為

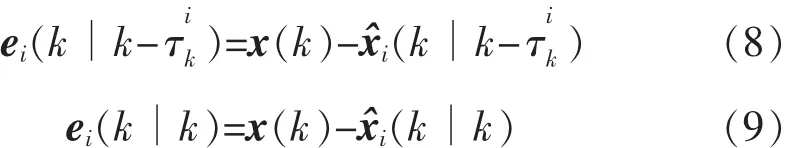
在實際工程應用中，由于噪聲和網絡因素的影響，傳統Kalman濾波器性能大大降低，且難以獲得全局最優估計。因此，需要設計具有時延和丟包的局部網絡化魯棒Kalman濾波器。文中將具有時延的量測分為一步時延（即＝1）和多步時延（即≥2）這 2種情形。

2.1 帶有一步時延的局部網絡化Kalman濾波

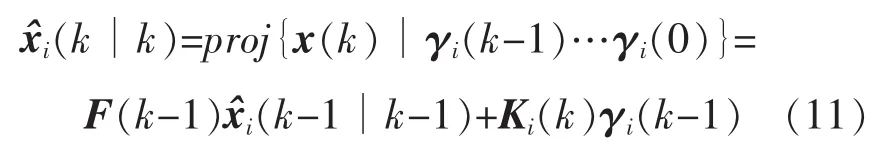
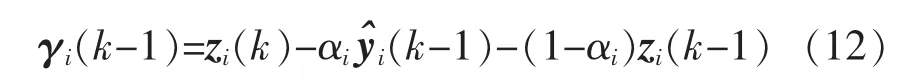
其中

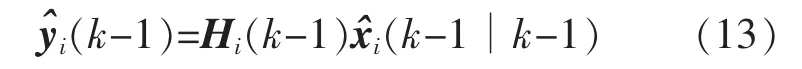
其相應的誤差協方差矩陣Ψi（k）為

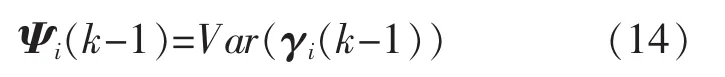
需要注意的是，與現存文獻中無時延Kalman濾波算法的不同之處在于，由于在k時刻估計器i收到 zi（k），其中 zi（k）由序列

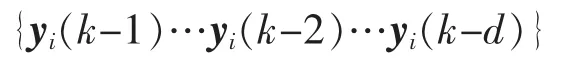
考慮到估計誤差的均值 E（ei（k∣k））＝E（x（k）-由于零均值白噪聲的特性 E（γi（k-1））=0，進一步可得 E（ei（k∣k））＝0，因此估計值是無偏的[10]。

定理1革新序列的誤差協方差可由式（12）和式（14）遞推得到

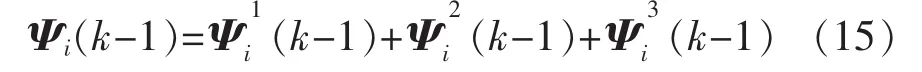
其中

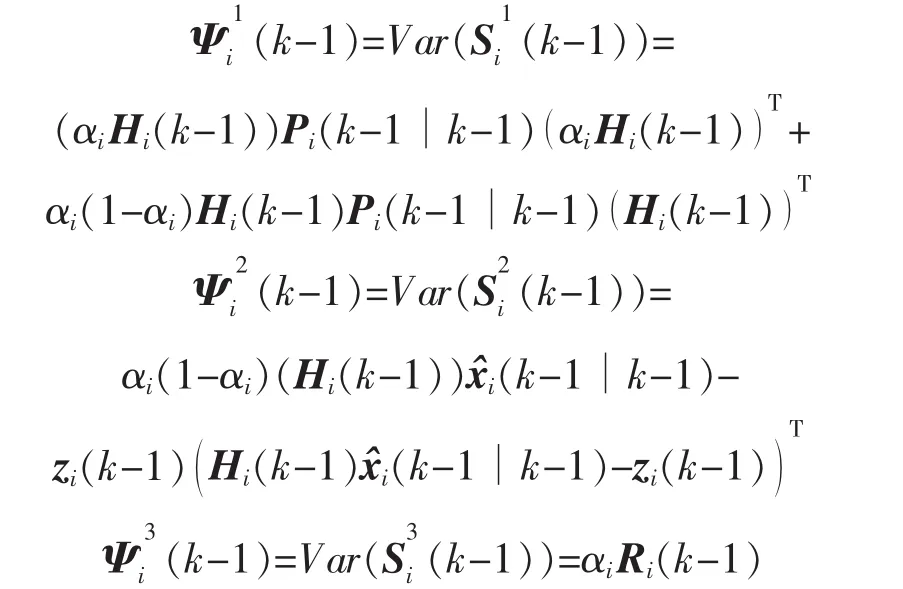
證明：將式（4）（7）代入式（8），則有

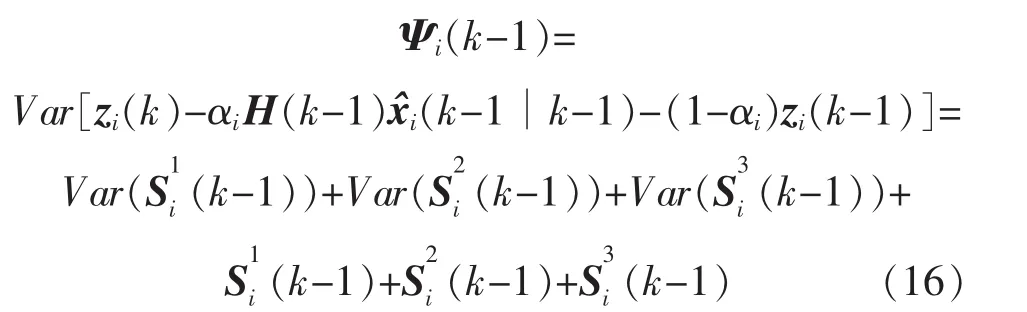
其中

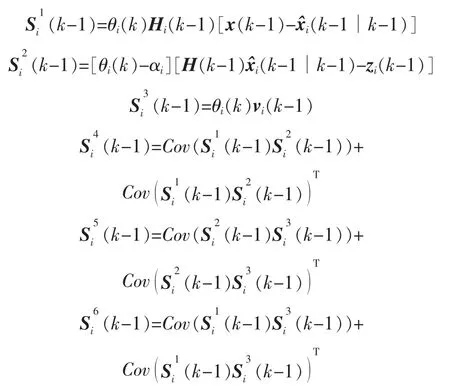
由于 x（k），w（k），vi（k）和丟包 θi（k）相互獨立，則

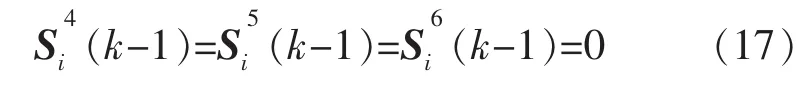
由式（16）（17）可得式（15），證畢。

定理2估計器i在k時刻的局部魯棒Kalman濾波可由如下遞歸方程給出

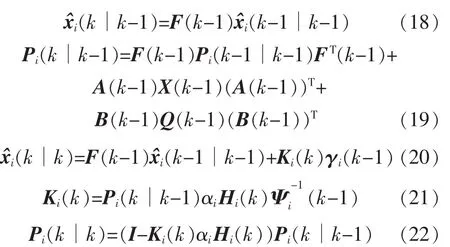
式中：Ki（k）為濾波增益；γi（k-1）為革新序列。

證明：將式（1）（18）代入式（8），可得

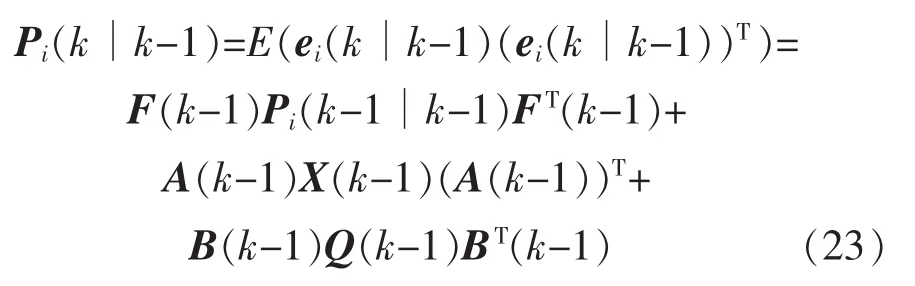
其中

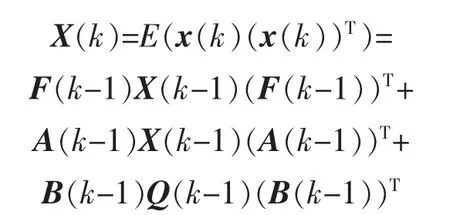
類似于Pi（k∣k-1）的計算，濾波的誤差協方差矩陣可得

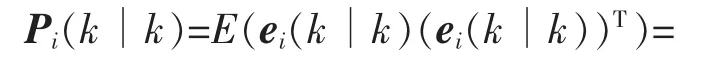
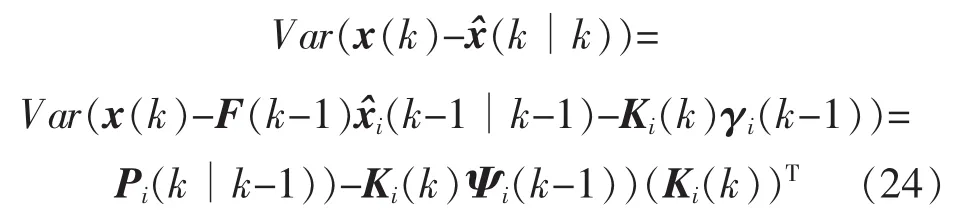
通過選擇適當的 Ki（k），可使濾波誤差Pi（k∣k）最小化。由

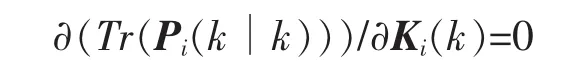
可得 Ki（k）；式中 Tr（·）為矩陣的跡，即

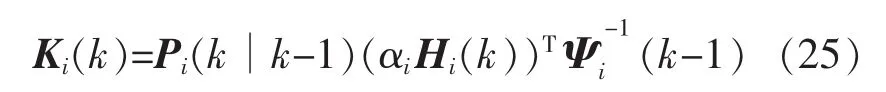
將式（25）代入式（24），可將 Pi（k∣k）重新寫為

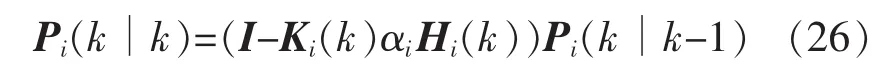
2.2 多步時延的局部網絡化Kalman濾波

傳感器的采樣數據通過網絡傳輸時，不同的傳輸時刻具有不同的隨機時延。當時刻k的時延2時，系統由重組的采樣數據和更新序列的多步預測進行局部估計。

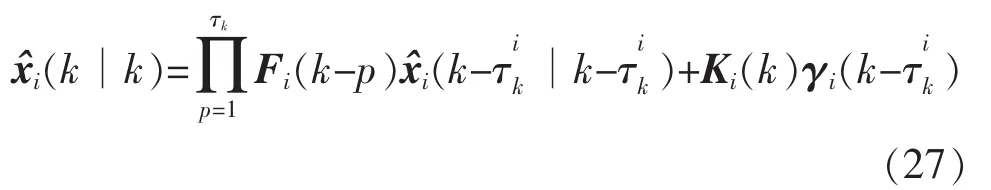
系統（1）可以重新寫為

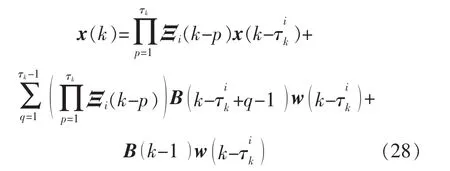
其中

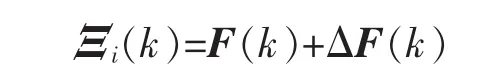
將式（27）（28）代入式（9），可遞推得到誤差協方差矩陣

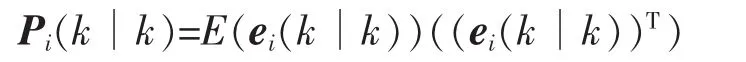
為了減少計算負擔，多步時延情形的融合估計設計類似于一步時延情形。

3 分布式融合估計

基于CI融合算法，在k時刻融合中心利用收到的估計器i和j的局部估計進行融合[6]，則融合估計和融合的誤差協方差矩陣 PCI（k∣k）為

式中：ωi（k）為優化權值系數，滿足，其可通過最小化性能指標 J=tr（PCI（k∣k））來確定。

算法1帶有時延和丟包的多傳感網絡化系統魯棒融合Kalman濾波。

輸入初始化局部狀態和誤差誤差協方差矩陣，并確定過程噪音和量測噪聲誤差協方差矩陣的初始值 Q（x）和 Ri（x）。

輸出局部狀態估計和相應誤差協方差 Pi（k∣k）。

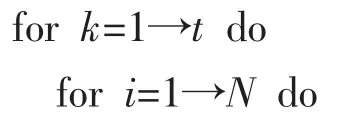
①傳感器i將采樣數據yi（k）傳輸給局部估計器，在此過程中考慮網絡化誘導時延和丟包現象，根據式（4）估計器端收到的采樣數據 zi（k）；

②根據式（12）計算基于一步時延即τk=1和丟包的革新序列 γi（k-1）；

③根據式（15）計算其相應的協方差 Ψi（k-1）；

⑤根據式（20）計算濾波增益 Ki（k）。

end for

for i＝1→N do

①利用補償機制，根據式（27）計算多步時延即τk≥2 的局部狀態

②結合式（28）計算相應誤差協方差 Pi（k∣k）。

end for

和協方差矩陣 PCI（k∣k）。end for

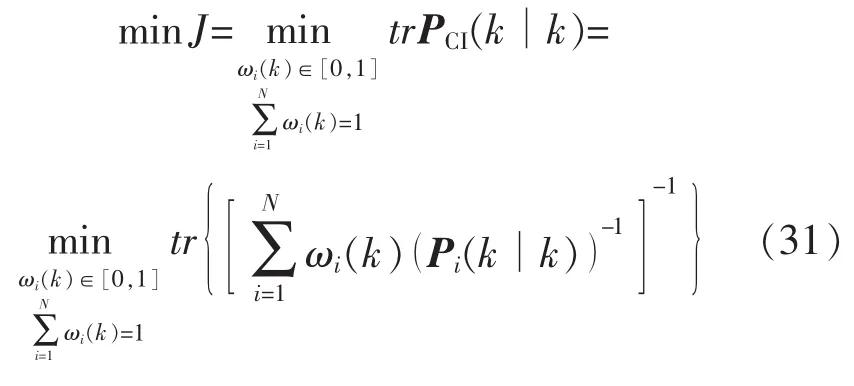
長期實踐表明，協方差矩陣偏離對角線的元素比對角線元素小很多，因此也可通過相應矩陣的跡來得到[6]，即

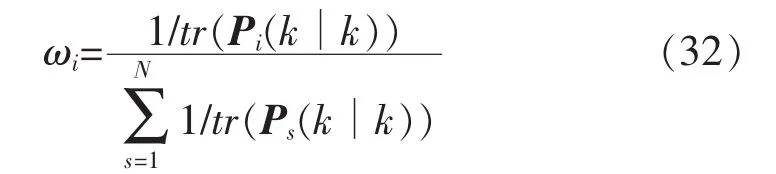
通過使用CI融合方法避免了交叉協方差的計算，減少了計算負擔。所提的分布式融合估計方法見算法1。

4 仿真例子

考慮基于傳感器網路場景中的移動目標追蹤問題。假設由3個傳感器節點分別對目標進行采樣，ΔF表示由移動目標的建模誤差引起的模型不確定性，系統可近似表示為

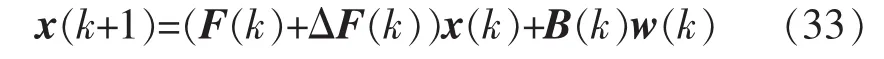
其中

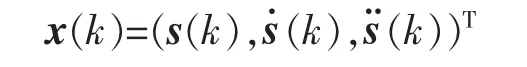
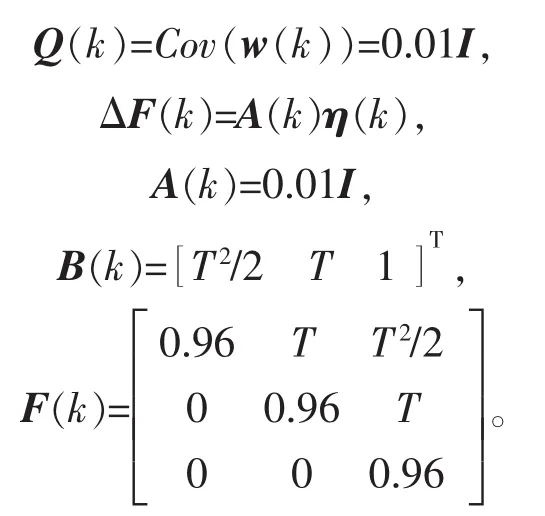
時刻kT傳感器i的采樣數據為

其中

式中：H1（k），H2（k），H3（k）為量測傳輸矩陣。

考慮傳輸過程的網絡化誘導特征，則相應的估計器收到的觀測值為

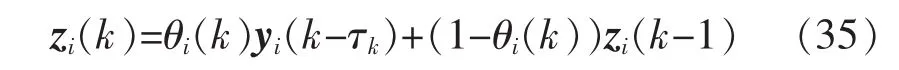
考慮τk=1的情形，假設系統的量測噪聲的協方差矩陣為

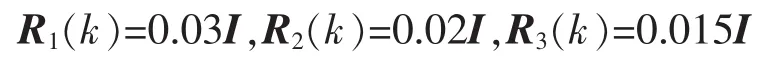
系統的初始值為

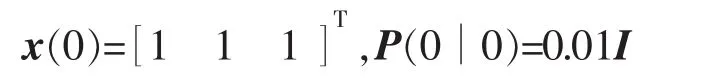
為了表明所提分布魯棒濾波的有效性，與分布式加權融合估計方法進行了比較。

假設，3個傳感器的數據包到達估計器的概率分別為0.72，0.76，0.74。系統的位置、速度和加速度的估計如圖2所示。

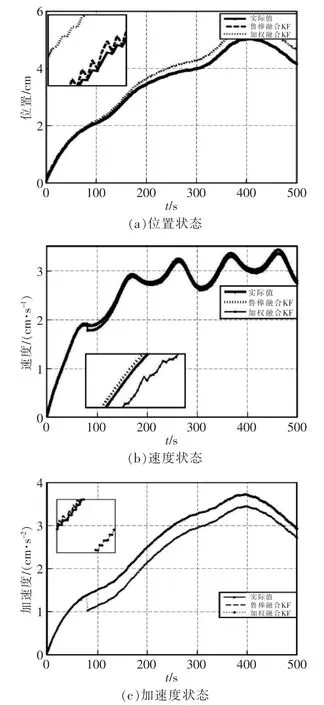
圖2 兩種方法對位置、速度、加速度狀態的估計Fig.2 Estimation of the state of position，velocity，acceleration by two methods

由圖可見，在考慮時延和丟包的情況下，本文融合估計算法具有很好的跟蹤效果。另一方面，局部估計和融合估計的誤差協方差如圖3所示，該圖揭示了融合估計的誤差方差陣的跡明顯小于各局部估計的誤差協方差陣的跡。由此，仿真說明了所提分布式魯棒Kalman濾波估計可以快速收斂到穩態，減少不確定干擾對系統產生的影響，且可提高系統的估計性能，即分布式魯棒CI融合估計方法具有更高的估計精度。

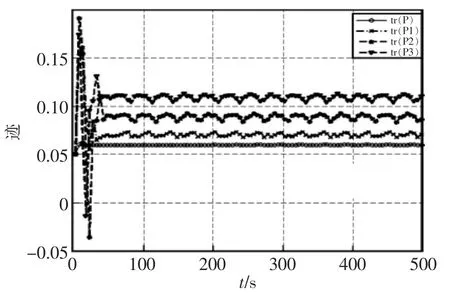
圖3 局部估計和融合估計的誤差協方差Fig.3 Error covariance of local estimation and fusion estimation

5 結語

針對具有網絡誘導傳輸時延和丟包的模型不確定性系統的分布式融合估計問題，設計了一種局部網絡化無偏Kalman估計器；在避免計算互協方差的情形下，利用CI融合方法將融合局部估計得到全局優化估計。仿真結果表明，融合中心的誤差協方差矩陣的跡比每個局部傳感器都小，融合估計精度更高。