基于GIS和地統計學的衡水市降水量空間變異性分析

陳 浩

(河北省衡水水文水資源勘測局，河北 衡水 053000)

0 引 言

隨機性與非線性是降水量在時空維度上呈現的主要特點，當前學者主要側重其在時間維度上的變化，采用信息熵、Mann-Kendall檢驗、趨勢分析、小波方差等方法對降水的傾向斜率、演變趨勢、震蕩周期等進行探討，而對其在空間上的分布特征研究不多。GIS和地統計學以空間自相關性變量理論為基礎，采用空間估計方法對降水量的全局特征進行估計。例如，原立峰等[1]采用高斯等模型對鄱陽湖流域降水空間分布進行全局預測，并發現其與地形之間存在顯著空間相關性；邵惠芳[2]介紹了變異函數和Kriging插值原理在降水空間變異分析中的應用，并試圖解釋其地帶性特征；李占玲等[3]運用地統計學原理研究了甘肅省近40年氣溫和降水的空間分布模型，發現降水和氣溫的分布中心發生季候遷移。衡水市地處華北海河沖積平原帶，受海陸位置與季風環流影響，區域降水呈現明顯的空間差異性，本研究借助地統計理論在GIS平臺上研究其空間分布模式，以期為區域水資源空間優化與調配提供依據。

1 資料與方法

1.1 資料來源

本研究中使用的氣象數據來源于中國氣象科學數據共享服務網站(http://data.cma.cn/site/index.html)。該數據由中國氣象局整編全國756個氣象站點，由于站點檢測起始時間不一致，部分站點數據存在較多遺漏，故而以研究時域為1989-2016年。衡水境內的站點有7個站點，時間分辨率屬逐日,各站點均無遺漏，質量可靠。

1.2 半方差函數

降水是典型的區域化變量，其在不同空間位置上具有相關、相似等特征，而這種特性是由結構性和隨機性綜合反饋而成。降水的空間結構性體現為其分布格局受環境過程影響表現出與之相應的規律性，隨機性則是脫離穩定機制之外而呈現的相對 ‘異常’特征。半方差函數是地統計學解釋降水空間格局分布規律的基礎[4]。其數學意義為給定間距h相隔的監測點測值之差平方的數學期望，定義如下:

(1)

式中：γ(h)為半方差函數值；h為不同觀測點對之間距離；N(h)為以h尺度下的所有觀測點對數量；Z(xi)和Z(xi+h)分別為位置xi和xi+h處變量監測值。

初始狀態下即h=0時，若存在以非零值C0，則稱為塊金方差，表征為系統內的隨機成分或實驗誤差；γ(h)隨著h的增加至A0時趨于穩定，γ(h)在該狀態下的函數值記作C0+C為基臺值，其中C為結構方差，表征系統內部穩定性，A0定義為變程，表征系統結構性影響范圍區間。其空間結構性可用塊基比C0/C0+C來度量，一般認為C0/(C0+C)<25%，表明變量具有強烈的空間相關性，25%～75%表明變量具有中等的空間相關性，>75%表明變量的空間相關性較弱；C0/(C0+C) <50%，表明結構性因素對變量的空間變異起主導作用，C0/(C0+C)>50%，則表明隨機因素是變量空間變異的主要原因。

1.3 分形維數

分形維數為變量分布格局復雜程度的度量，其數學定義為變量變異函數的雙對數關系logγ(h)∝logh在一定觀測尺度h上的線性關系[5]：

(2)

式中：H為線性斜率，取值為[0,1]；FD為分形維數，值域(1，2]，FD隨著H的增加而減小。

對于區域降水空間分布，其分維數越小則其分形越好，表明降水分布趨勢性強，空間漸變性、連續性好；其分維數越小，則其分形特征越長，表明區域降水異質格局強，分布離散、連續性差、全局趨勢弱。

1.4 研究數據源與處理平臺

本文采用Excel2016軟件對降水資料進行描述性統計分析，SPSS 21.0用于Kolmogorov—Smirnov法的正態分布檢驗，對于未能通過5%水平雙尾檢測的序列數據進行轉換，使之符合地統計分析需要。地統計分析中，半方差模型擬合與參數計算、空間分維數計算在GS+9.0中進行，Surfer 13.0中完成普通Kriging 插值分析。站點數據只能反映局域降水信息，為直觀顯示其全域空間格局，采用Kriging插值法并以高程作為輔助進行無偏最優估計。

2 衡水市降水量空間變異性分析

2.1 衡水市降水量統計特征

表1為1989-2016年衡水市7個氣象站點的降水年月數據統計結果。由表1可知，28年間年度總降水量在331.3～849.32 mm之間，總體均值為524.8 mm，其變異性較小，僅為10%，表明年際氣溫變化不大，呈弱變異。各個季度內，全省降水量描述性統計較為一致，如最大值、最小值、標準差、均值等，表明降水分布的季節性不均衡，同時季節內部變率較小。從分布形態上看，除了1-4月份的數據為負偏態，其余為正偏態；峰度系數表明1、4、5、9、11月份的數據為緩峰分布，其余為尖峰分布，K-S檢驗表明，9月份的降水數據符合正太分布，余者均不符合。在后續進行空間結構、分形維數、 空間自相關分析的時候，需要將其進行對數或者均方差轉換，使其符合正態分布形式。從變異系數來看，2、5、6月份降水變異較小，介于16%～20%之間；1、3、4、7、11、12月份變異程度居中，介于20%～30%之間；8-10月份降水的變異系數高于30%，變異程度為最高。

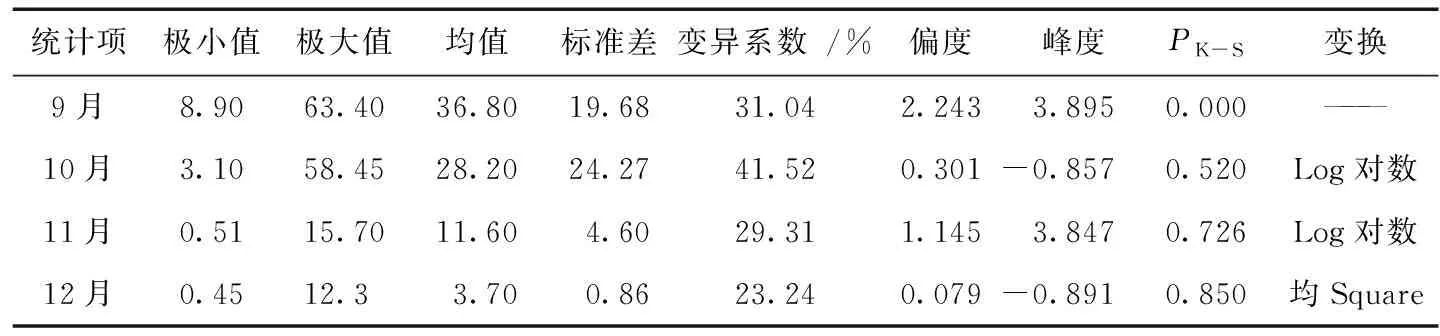
續表1

2.2 衡水市降水空間結構特征

半方差函數計算時需要設定其滯后距離總長和步長，通常認為其步長應該大于最小觀測距離，滯后距離小于最大觀測距離的1/2。經計算測站之間的相對距離，設定其參數值分別為40、600 km。GS+9.0中提供了高斯、線性、球面、指數4種空間擬合模型，其中大部分的時間序列降水符合高斯模型，個別年份以指數模型擬合最佳。為便于比較同質條件下年降水空間結構差異，經過對數變換后均采用高斯模型。該模型能夠擬合較大觀測尺度變量分布特征，穩定性較好。結果顯示，決定系數R2介于0.893～0.982，殘差RSS小于10-2，表明高斯模型擬合程度高，能夠揭示區域年降水的空間結構。見圖1。

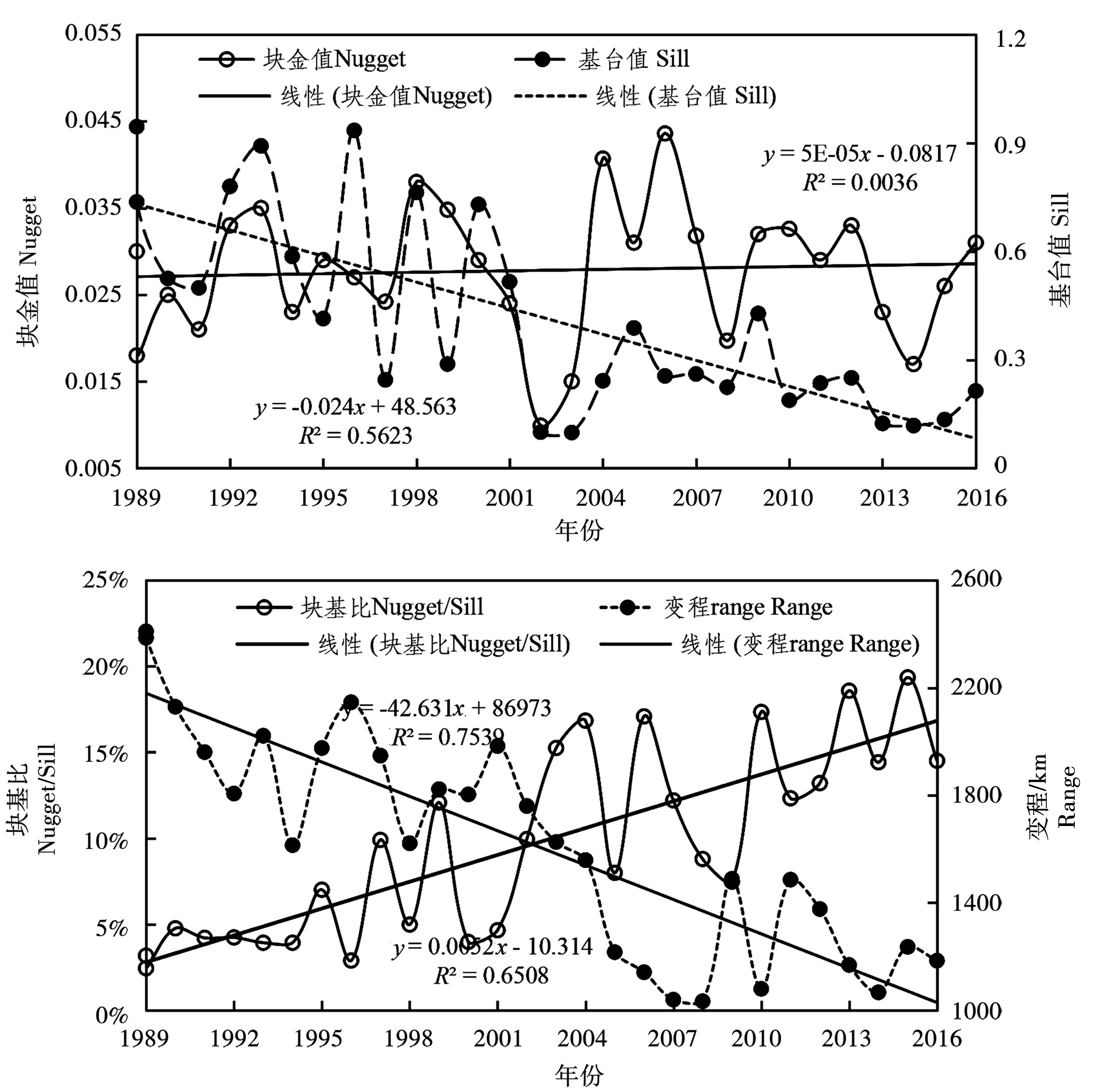
圖1 1989-2016年衡水市降水量半方差結構參數變化趨勢

由圖1可知，各時間序列內研究區年降水量空間分布存在一定的塊金方差，其值介于0.015～0.043 6之間，表明降水過程受到一定隨機因素如氣候異常、人為干擾的影響，但其變化趨勢并不顯著；而基臺值介于0.098 4～0.935之間，以y=-0.024x+48.563的形式呈逐漸減小(R2=0.562 3,P<0.05)，說明其內部結構性規律減弱。28年間各年度降水量的塊基比均小于25%，說明其空間分布特性具有強烈空間自相關性，反映了衡水市降水空間分布受自然因素(氣候過程、水循環、地形、海陸位置等)控制，但塊金效應以y=0.005 2x-10.314的形式線性增強(R2=0.650 8,P<0.05)，由此可知其結構性逐漸減弱、隨機性趨于增加。28年間變程的變化范圍介于1 033～2 410 km之間，綜合趨勢以y=-42.631x+86 793的形式遞減變化，由此可知衡水市降水空間自相關范圍減小，表明其分布格局破碎化程度高、異質性強，領域之間相關性削弱。

2.3 衡水市降水空間分形維數特征

分形維數作為區域化變量空間分布格局復雜度的度量，其值越大表明降水的空間分布越復雜，空間異質性越強。應用前述分形維數方法，得到1989-2016年衡水市降水量分形維數變化趨勢，見圖2。由圖2可知，2002年全市降水量的分形維數最小，僅為1.531，表明該年降水量空間分布最為簡易，全市降水量分布差異性小；而2016年其分形維數最大，達到1.792，說明該年度降水量空間分布最復雜，全局降水量差異性巨大。研究時域內分形維數的均值為1.634，其呈y=0.007 9x-14.09，R2=0.716 6的形式變化，說明近28年來全市降水分布復雜性呈線性增加，且達到顯著性(P<0.05)。

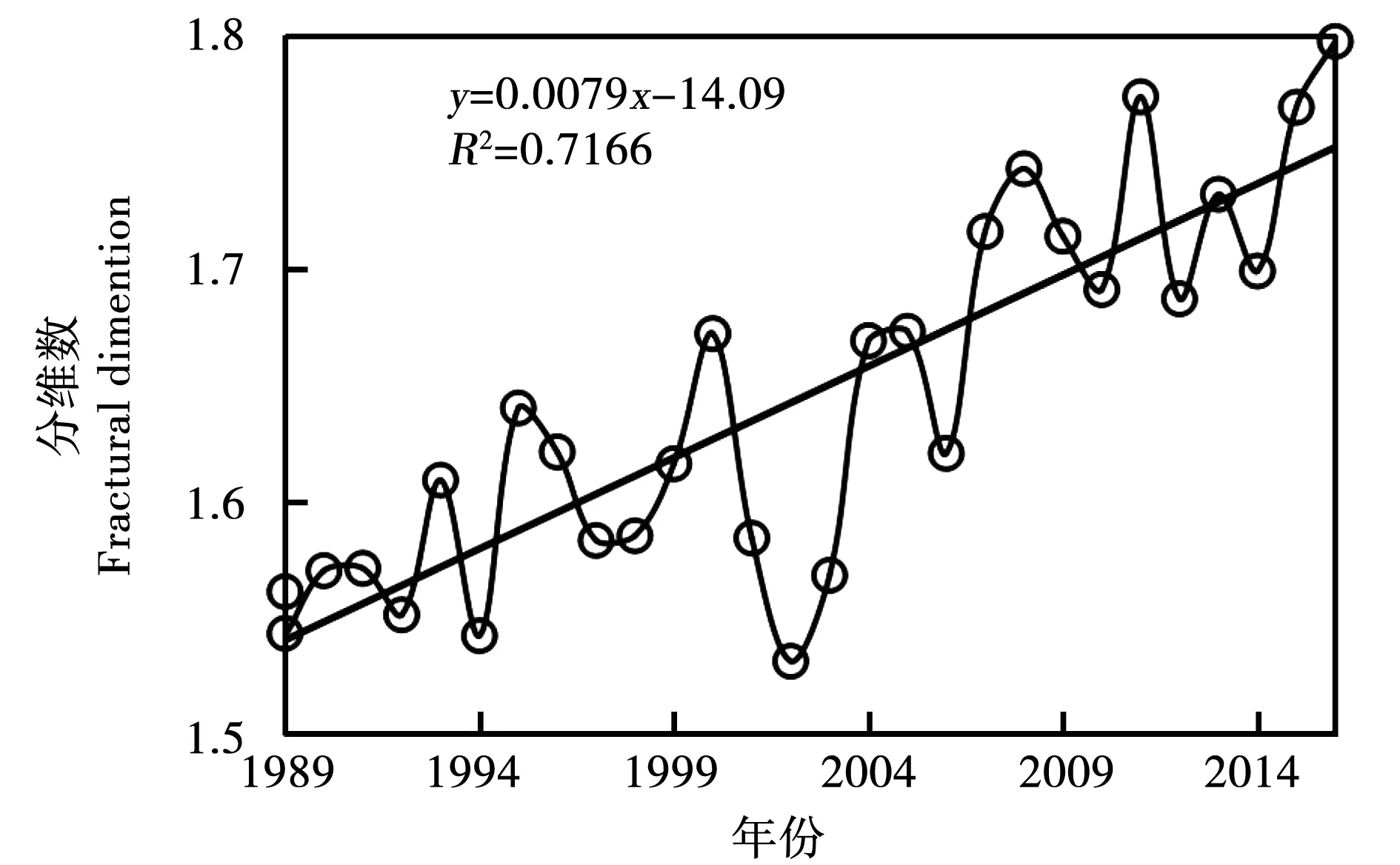
圖2 1989-2016年衡水市降水量分形維數變化趨勢

2.4 衡水市降水量空間分布特征

衡水市面積廣闊，域內雖然地貌形態差異不大，但是經緯度相差略遠、與海洋距離位置不一，加上全市下墊面環境差異大，這就使得區域降水量空間分布存在異質性。以1989-2016年各站點年降水量平均值為基礎，在Surfer13.0軟件上采用普通Kriging插值法進行全局預測，得到衡水市降水量空間分布圖，結果見圖3。由圖3可知，全市以安平縣降水量為476.2 mm，為全市最低；其次為棗強縣，達481.5 mm；市轄區的冀州區與武邑縣、饒陽縣的降水量相差不大，在510～515 mm之間；而武強縣、故城縣、景縣的降水量明顯高于其他地區，達到554.2、558.3和552.6 mm。總體而言，全市降水空間分布不均衡，由東向西遞減。

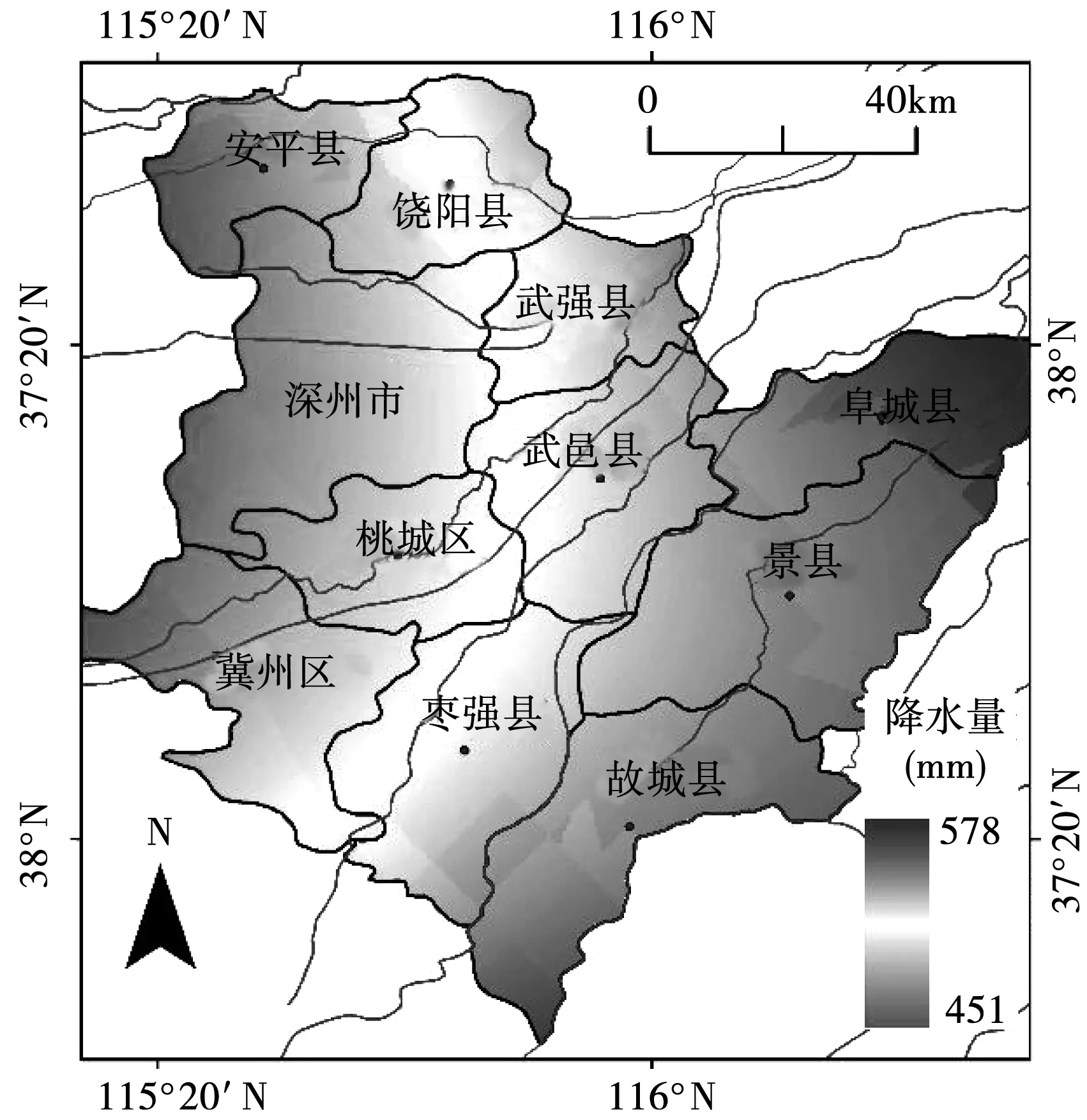
圖3 衡水市降水量空間分布格局

3 結 論

受水循環過程、海陸位置依據區域地理環境等因素影響，降水在空間上分布呈現出不均衡性，地統計學以區域化空間自相關理論能夠定量解析其空間結構性規律和空間布局。本研究表明，1989-2016年來衡水市降水量的空間分布結構性規律趨于減弱，且其空間分布越來越復雜；近28年來全球氣候變化加劇，導致局部降水的不確定性和隨機性加強，表明全市降水空間分布的不可測性增加，這與相關學者的研究結論相一致。衡水市降水空間分布的隨機性增加，意味著該地區極端降水的發生概率增大，因此今后應注重災害防御和區域水資源管理對策的調整。