基于出口選擇概率的修正社會力模型的行人疏散研究

霍富昌，姜志俠，謝繼軒，張時赫，薛天坤

（長春理工大學 理學院，長春 130022）

社會力模型是一種應用廣泛、仿真效果最接近實際情況的行人運動模型。社會力模型可以對行人在實際疏散過程中表現出來的模式和行為進行仿真模擬[1-3]。大量學者對社會力模型進行研究，陳濤等為解決原有社會力模型中存在的速度振蕩問題，引進相對速度對原始模型進行優化[4]。汪蕾等引進了相對速度，并引入恐慌因子對行人的期望速度進行修正，得到了社會力修正模型，在一定程度上，能夠較好的仿真突發事件下的行人疏散運動[5]。

雖然社會力模型有著眾多的優點，但其也存在一定的局限性。尤其是在行人疏散過程中，原始模型沒有有效的機制來防止行人重疊現象，而且當行人密度較大或較小時，會發生一些不符合實際的現象。

基于原始社會力模型，引入緊張因子、相對速度以及出口吸引力對社會力模型進行修正，然后借鑒元胞自動機模型，建立防重疊機制并確立相應的出口選擇機制，最后建立多出口行人疏散綜合模型，對多出口場所內的行人疏散行為進行仿真模擬。

1 模型

1.1 原始社會力模型

Helbing的社會力模型基于牛頓第二定律，行人i所受合外力fi（社會力）是由行人自身驅動力、行人與行人間的相互作用力f、人與障礙物ij間的作用力fiω三個力聯合產生，由此建立物理方程[6]：

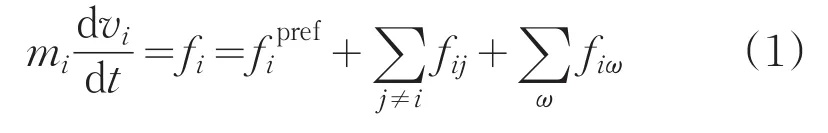
式中，mi代表行人i的質量，vi代表行人的實際速度。

（1）行人自身驅動力

行人自身驅動力是指行人i在期望時間τi內以實際速度vi向期望速度前進，具體物理方程為：

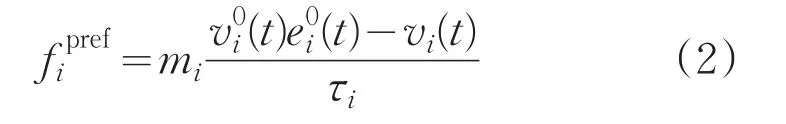
（2）行人與行人間的相互作用力

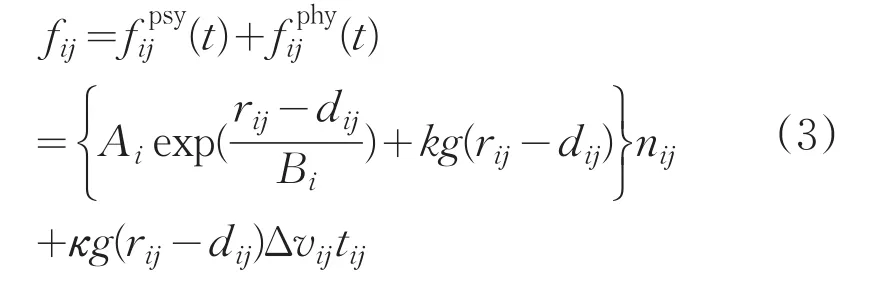
式中，Ai、Bi、k、κ為常量參數，rij=ri+rj代表行人i和行人j的半徑之和，代表行人i和行人j質心間的距離，代表由行人j到行i的單位向量，切向向量從而，g(x)是一個分段函數，具體函數如下：

（3）人與障礙物間的作用力

與行人間的作用力類似，人與障礙物間的作用力fiω可表示為：

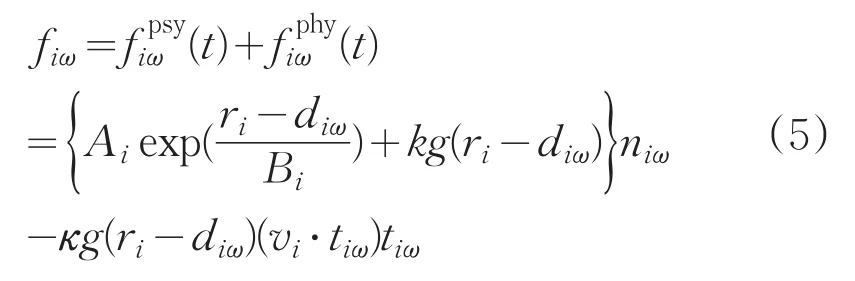
同樣，對于墻或障礙物而言，diω代表行人i的質心到障礙物表面的距離，代表障礙物指向行人i的單位向量，切向向量。

1.2 修正社會力模型

針對社會力模型中存在的問題，以及結合現實行人疏散行為，對社會力模型做出一些修正。

（1）期望速度修正

在實際的疏散場景中，行人的期望速度往往不是一成不變的，Helbing加入緊張因子ni(t)來對期望速度進行修正，行人的期望速度可修正為[3]：

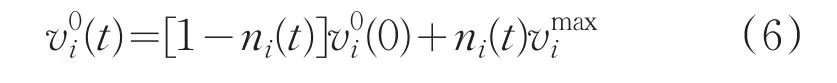
（2）相對速度修正

基于陳濤對相對速度的分析，結合Helbing的社會力模型，考慮相對速度對行人疏散過程中的心理作用力的影響，則社會力原模型中行人與行人間的相互作用力fij及行人與障礙物之間的相互作用力fiω分別可修正為[3]：

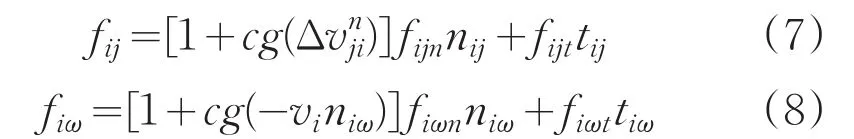
式中，fijn和fiωn稱為法向社會心理距離作用力，稱為法向社會心理速度作用力。表示疏散人員i和疏散人員j的法向速率差。為相對速度影響系數，代表速度力與距離力的比例關系。

（3）引入出口吸引力

Lakoba認為出口會對行人產生吸引力fik，其具體表達式為[7]：

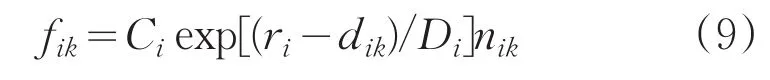
式中：k代表出口，Ci為常數。

類似相對速度優化中相對速度的影響，在此定義門的相對速度影響系數Ck，其中因門無法移動，只有人員i會移動，從而簡寫為。同時結合原模型fik可得優化公式：

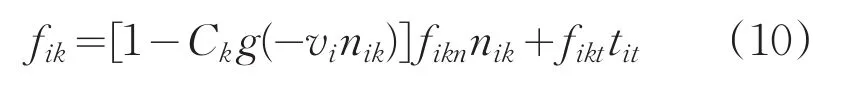
社會力模型修正為：

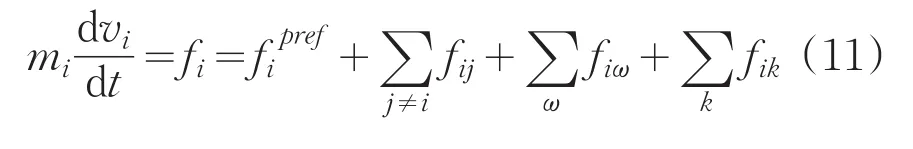
2 出口選擇

在對社會力模型的研究中發現，社會力模型在仿真過程中會出現行人重疊現象，因此參考元胞自動機模型將場所化為網格，規定一個行人只能占據一個網格，且行人不能直接越過網格，以來建立簡單的防重疊機制[8-11]。

為了解決出口利用不均勻的問題，通過考慮行人與出口的距離以及出口處行人密度對出口選擇的影響，基于概率決策，參照文獻[12]和[13]，引入出口選擇函數：

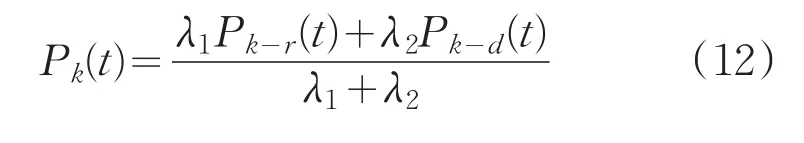
式中，

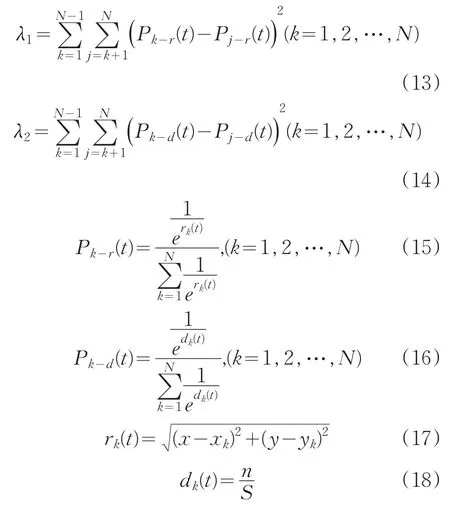
式中，Pk(t)為t時刻選擇出口k的概率，λ1是距離指數，即概率Pk-r(t)占Pk(t)所對應的比重，λ2是密度指數，即概率Pk-d(t)占概率Pk(t)所對應的比重，Pk-r(t)是只考慮行人距離時行人在t時刻選擇出口k的概率，Pk-d(t)是只考慮行人在出口區域的人員密度時行人在t時刻選擇出口k的概率，rk(t)是行人距離出口的距離，dk(t)是出口區域處的人員密度，N是出口總數。

3 構建多出口行人疏散模型

基于修正后的社會力模型，結合出口選擇機制，構建多出口行人疏散優化模型，具體模型如下：社會力模型即公式（11）中各修正項由公式（2）、公式（6）、公式（7）、公式（8）和公式（10）構成。出口選擇函數是由公式（12）、公式（13）、公式（14）、公式（15）、公式（16）、公式（17）和公式（18）構成。

當某時刻行人與出口的距離相等且各出口區域處人員密度也相等時，則有：

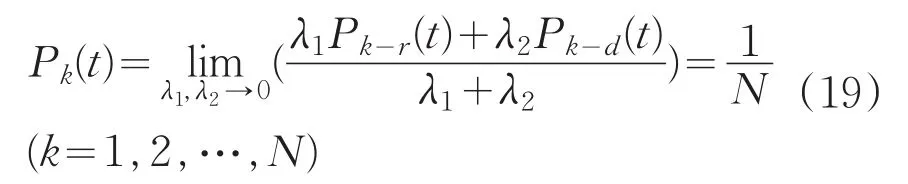
此時行人選擇各出口的概率均相等。此時判定選擇的出口，以行人i建立坐標系，比較各出口對于行人i位置的方向m與社會力方向fi的夾角θ大小，夾角最小的即為所選擇的出口。

出口選擇函數對出口引力進行比重均衡，比較概率，最可能選擇出口與行人行進方向是否一致，即朝向出口的Pk(t)最大為不改變出口選擇。若行人改變出口則不考慮此出口引力，將剩余出口引力均衡計算，重新模擬該時段；若不改變，則按原步驟繼續進行，繼續下一個時段模擬，以此循環，直至行人通過出口結束。模型模擬流程圖如圖1所示。

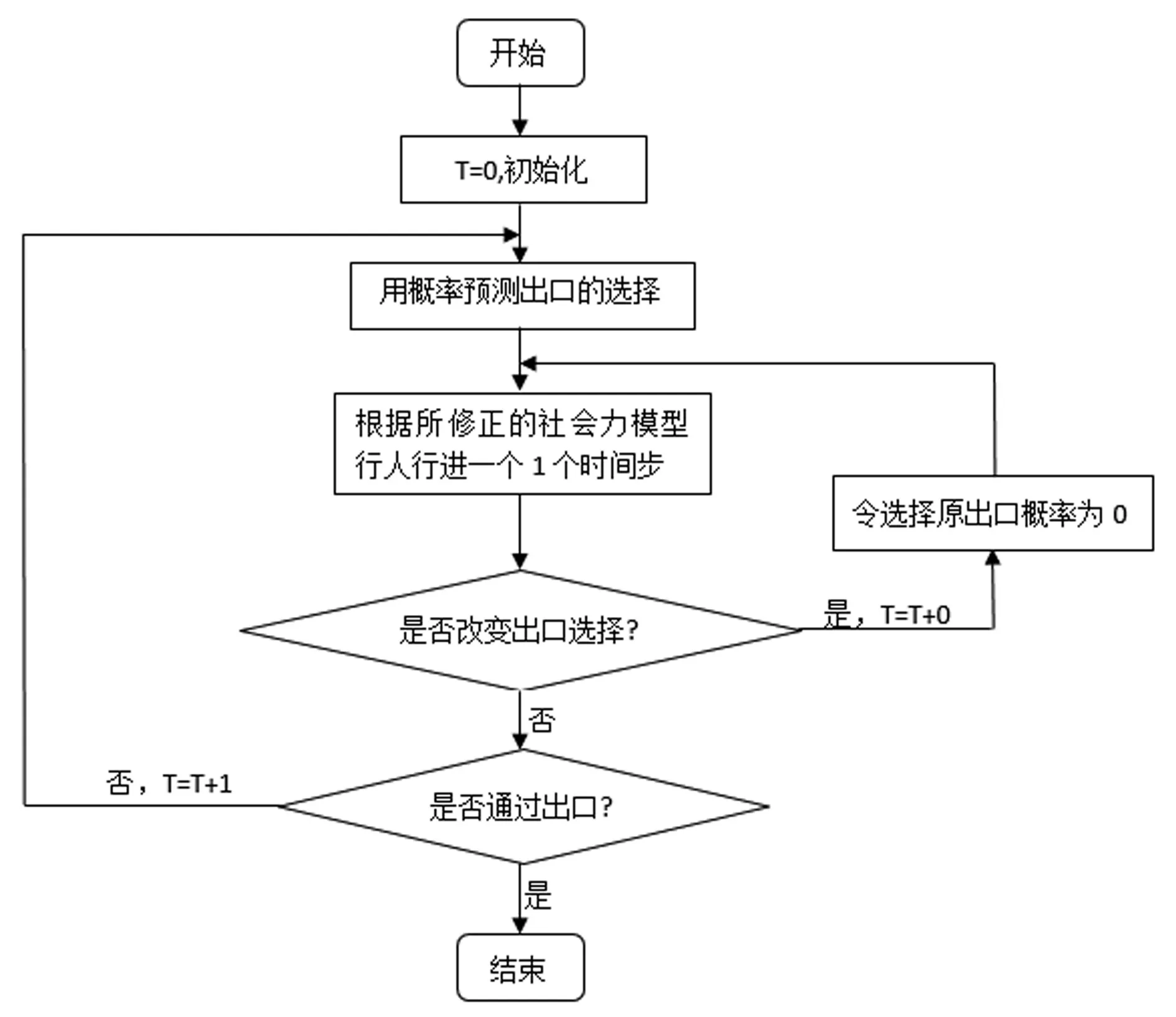
圖1 行人模擬過程流程圖

4 模型應用分析

4.1 仿真模擬

為了驗證提出的基于出口選擇概率的修正社會力模型的科學性和可用性，進一步通過仿真模擬來進行模型應用分析。選取15m×15m的房間為疏散環境，假設該房間內有兩個出口A、B，兩個出口規格相同。設置初始疏散人員為100人，隨機分布在房間內，初始分布如圖2所示。

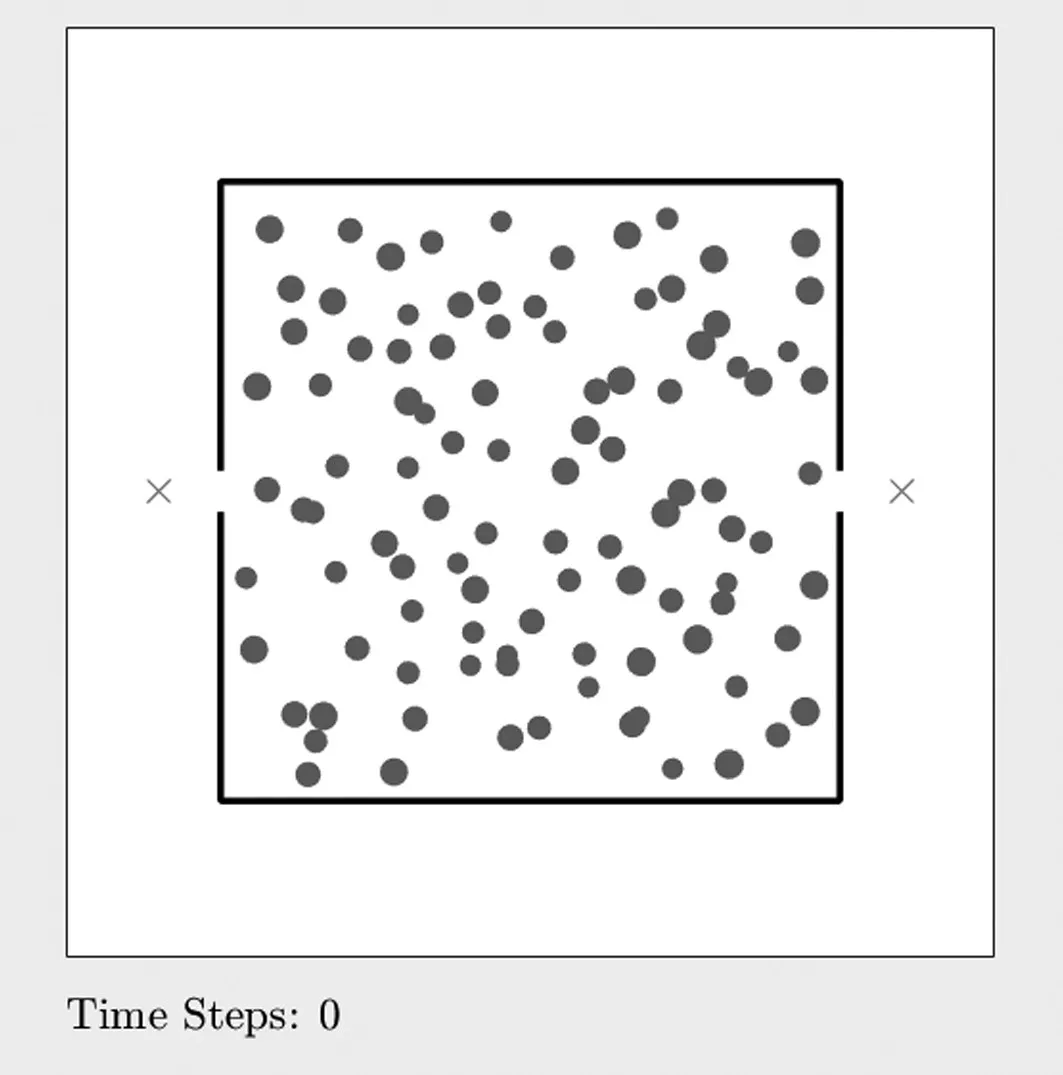
圖2 行人疏散模擬初始分布示意圖

在疏散開始階段，行人選擇出口時主要是根據到出口的距離，并且在一段時間內更換出口的可能性較小，從而會出現行人呈半圓形聚集在出口位置，行人大致會分為涇渭分明的兩部分，如圖3所示。然而隨著疏散進行等到大量行人聚集在出口位置時，距離因素已不是行人選擇出口的主要因素，出口處行人密度成為選擇出口的主要因素，部分行人將會放棄距離最短的出口而選擇出口處行人較少的出口進行疏散，這與現實生活中的行人疏散情景相符合。

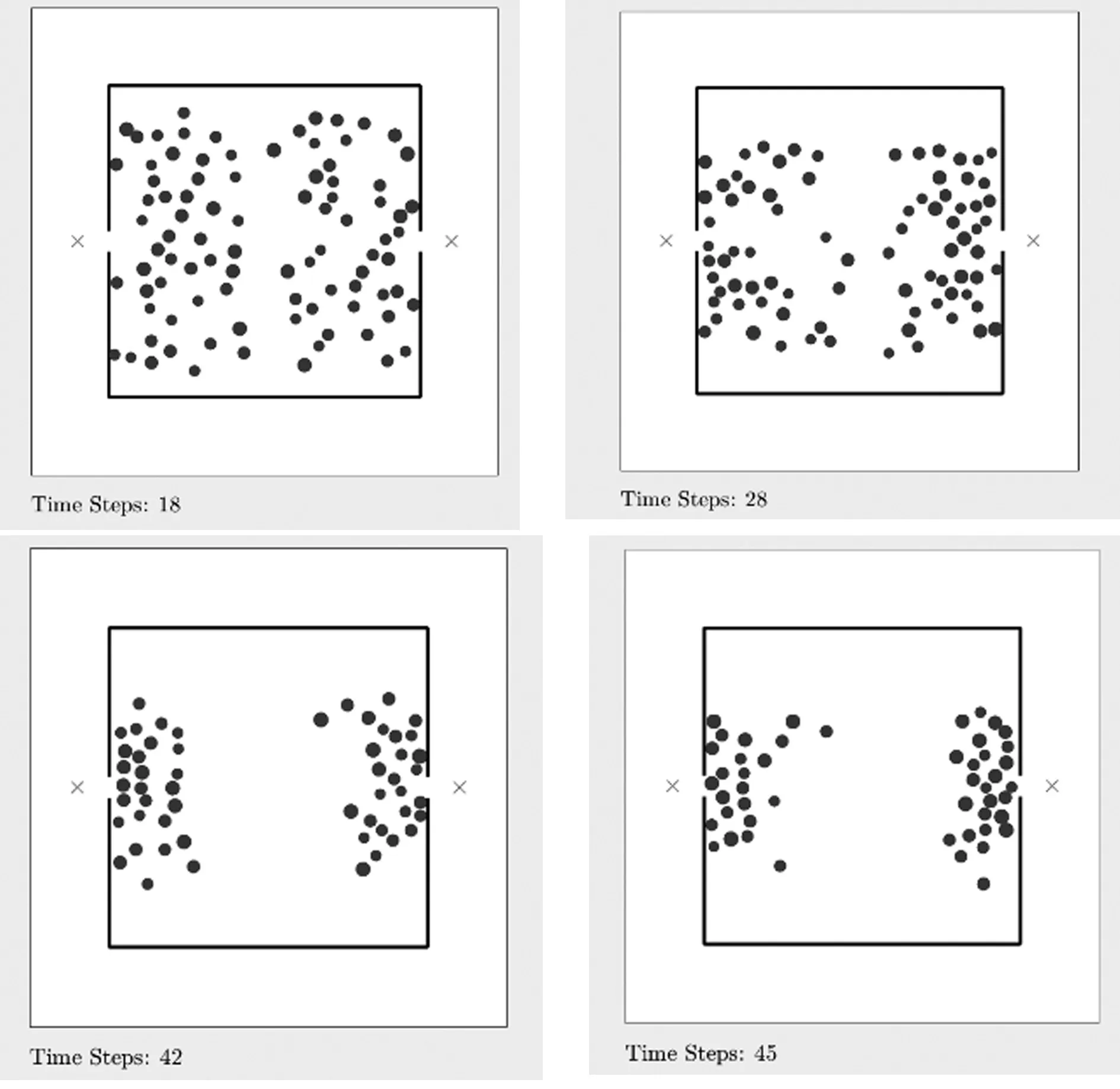
圖3 行人疏散過程示意圖

4.2 討論分析

對多出口綜合模型進行討論分析，對比三種模型的疏散效果，即方案1（不使用社會力只基于概率決策的出口選擇的理想模型）和方案2（不使用出口選擇函數只使用修正后社會力模型）進行仿真模擬（具體方案如表1所示），得到結果如表1所示。

表1 不同的出口選擇方案中各出口承擔的疏散人數（人）

表1表示行人選擇不同疏散方案時的各出口承擔的疏散人數。對比圖表發現，方案1中，是純理想化狀態，行人不受外界其他因素影響，只考慮距離和行人密度，因此各出口承擔的疏散人數相等。但在現實情境中行人的疏散卻是受到多方因素的影響，各出口承擔的疏散人數明顯不相等。方案3中各出口承擔的疏散人數趨于相等，這是優化后的綜合模型，這與實際相符，說明優化模型和算法的正確性。

為了驗證模型的有效性，分別選取疏散場景為15m×15m（場景1）、15m×30m（場景2）、30m×30m（場景3），對這三種場景下的行人疏散進行研究。

統計在不同疏散場景種不同模型的疏散時間，用來分析三種模型所得的出口優化方案對疏散效率的影響，得到了三種模型下的行人疏散的總時間，結果如下表所示。

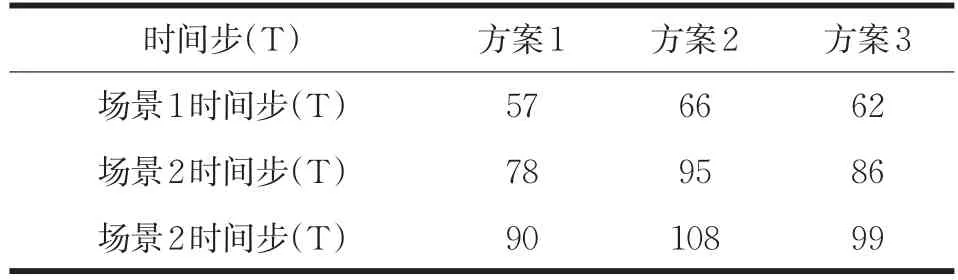
表2 不同模型不同場景下行人疏散總時間

由表2可知：在不同的疏散場景中，方案1是最為理想的狀態，時間最短，但這種狀態在現實情景中不可能出現；方案2行人疏散所花費時間最長，疏散效果最差；方案3時間趨近于方案1，比較合理，接近理想化疏散。

行人在實際的疏散過程中選擇出口是受多種因素的影響，往往由于出口處行人過多導致疏散效率過低。在模型中加入基于概率決策的出口選擇函數，實質是考慮行人與出口的距離以及出口處行人的密度對行人出口選擇的影響。在行人進行出口選擇時，行人將會綜合考慮行人與出口距離及出口處行人密度等因素，選擇一個對行人自己相對有利的出口進行疏散，從而達到一個比較理想的效果。模擬結果顯示：引進基于概率決策的出口選擇函數更能真實反映多出口選擇下行人的疏散行為。

5 結語

基于實際情形以及社會力模型的復雜性，本文引進相對速度和出口吸引力以及對期望速度加以限制來對社會力模型進行修正，并且建立了簡單的防重疊機制，引進基于概率決策的出口選擇函數，構建了基于出口選擇概率的修正社會力模型，對行人疏散問題進行研究。通過進行仿真模擬，構建的多出口行人疏散綜合模型能夠較好的反映現實場景中的行人疏散行為，與實際行人疏散行為相符合。因此，該模型具有重要的意義和參考價值。