基于球面矢量的四元數姿態插值
普亞松 張文斌 郭德偉 閔 潔
(1.紅河學院 工學院 云南省高校高原機械性能分析與優化重點實驗室;2.西北工業大學 現代設計與集成制造技術教育部重點實驗室)
姿態運動軌跡規劃是工業機器人一項重要內容。本文提出用單位球面上的三維矢量進行姿態四元數插值,描述了該方法的推導與使用步驟,結合單位球面上的三維矢量,對四元數插值姿態的合成進行說明。算例驗證了該插補方法合理可行。
引言:工業機器人末端執行器在工作空間的運動軌跡規劃是一項重要的內容,合理的運動軌跡對工業機器人的工作質量、效率和使用壽命有著極大的影響。工業機器人末端執行器的運動軌跡規劃分為位移規劃與姿態規劃,姿態規劃比位移規劃更為復雜,本文僅對姿態插值規劃進行研究。
剛體運動姿態的表示方法主要有旋轉矩陣、歐拉角和四元數。四元數描述姿態主要有如下優點:1)避免萬向節鎖死現象;2)運算效率更高;3)便于提供平滑插值。所以四元數大量運用以各種旋轉的場合,目前已成為主流趨向。
姿態插補的一般方法是球面線性插補(Slerp),該方法推理與運用都比較簡單,但不直觀形象,四維向量夾角的物理意義不明顯。本文采用球面矢量進行四元數姿態插補,用三維矢量直觀表達四元數,有助于理解四元數姿態合成的過程,并能夠實現姿態平滑插值。
1.四元數與轉動
四元數一般表示方法為:
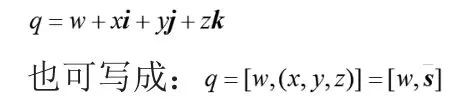
w稱為四元數的實部,稱為四元數的虛部或向量部。實部為零,即w=0時,四元數稱為純屬四元數。
任意兩個四元數:
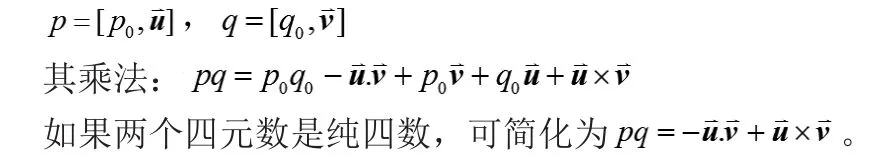
單位四元數可以用轉角與轉軸表示:

其中θ為轉角,為轉軸矢量,公式里帶入的角度值為轉角的一半。如圖1a所示,剛體上一點,繞轉軸 ,轉動θ角,轉動之后新的位置點為,該轉動過程用數學方程描述為:,其中S1,S2分別為組成的純四元數,四元數物理意義明顯,一個四元數對應一個轉動。
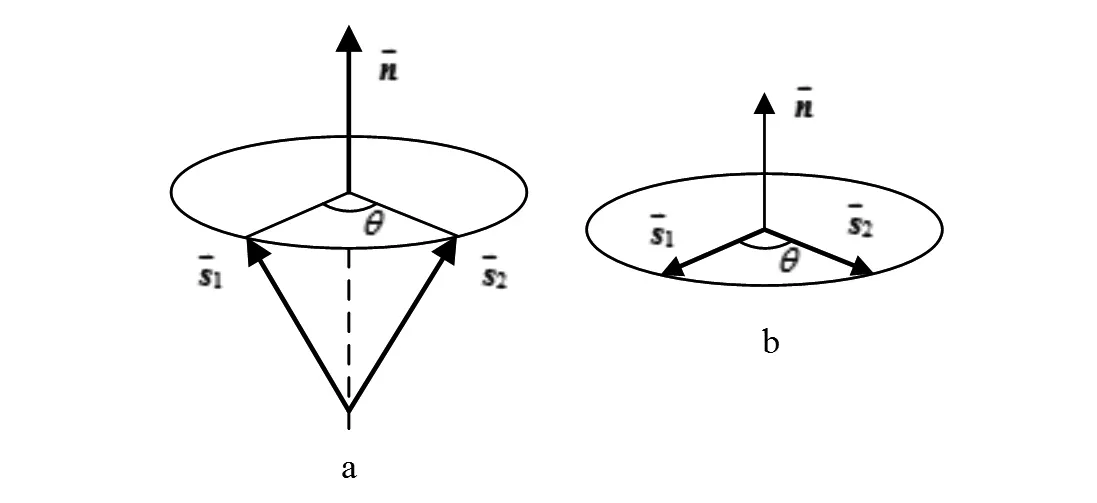
圖1
如果被旋轉的矢量與旋轉軸正交,如圖1b所示,則轉動過程用數學方程描述為:,此時的四元數格式變為:。正交書寫格式可以相應地轉換為非正交的格式。
2.矢量法四元數姿態插值的原理與步驟
2.1 姿態與四元數
剛體轉動之后,不僅是剛體上質點的位置坐標發生了變化,而且剛體的方位,也即姿態,也會發生相應的變化。一個四元數對應一個轉軸與轉角,也就意味著發生了一個轉動,對應著一個姿態。剛體連續轉動,每一個轉動對應的四元數分別為,最終合成的姿態qe,。剛體無論發生多少個轉動,可視為最后合成一個轉動,可由一個轉軸與轉角一次性轉動到位。
剛體姿態插值時,已知剛體初始姿態,可理解為經歷一個轉動,對應四元數為qs。還知道結束姿態,也理解為經歷一個轉動,對應的四元數為qe。初始姿態再經歷一個過渡轉動(對應四元數為qm)之后變為結束姿態,也即,初始姿態的轉動再疊加一個過度轉動可合成為一個結束姿態的轉動,。均勻分配中間過渡轉動,能得到一系列的末尾插值姿態qei,。
2.2 單位球面矢量表達四元數
剛體姿態插值時,知道初始姿態與結束姿態,對應四元數分別為qs,qe,可求初始姿態與結束姿態之間過渡轉動的四元數qm,,可得到過渡轉動qm的轉角θ和轉軸。
綜上所述,初始姿態與結束姿態之間過渡轉動的四元數qm,可由單位球面上垂直于過渡轉動轉軸的兩個旋轉向量表示。如圖2所示,兩個旋轉向量垂直于轉軸,夾角為轉角θ,一個向量旋轉到另一個向量時,在單位球面上形成一段圓弧,這兩個向量及圓弧就表示過渡轉動的四元數qm。均勻分配圓弧上的點,則可以得到均勻分配得到一系列過渡轉動四元素qmi,與初始姿態疊加之后,得到一系列均勻的插值姿態qei。這樣,四元數在超復數空間S3轉化為歐氏空間單位球面上的圓弧及其向量,直觀形象,有肋于理解姿態插值以及合成過程。
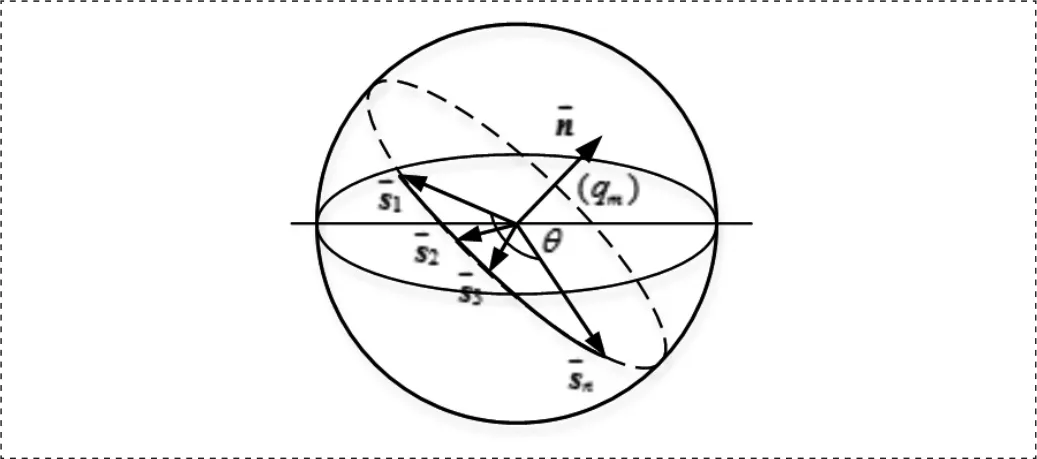
圖2
2.3 單位球面上的空間圓弧參數方程
再結合本研究的需要,單位球面上的空間圓弧可表示為如下方程。

2.4 矢量法四元數姿態插值的步驟
1)由給定的初始姿態與結束姿態得到過渡轉動的轉軸矢量與轉角,相關方程為。
2)由空間圓弧參數方程,在旋轉圓弧上取一系列均勻的點,相關方程上述。
3.算例驗證
算例:已知工業機器人未端執行器繞定軸X轉30度為初始姿態,繞定軸Y轉45度為結束姿態,均勻插值中間姿態。
根據上述方法與步驟,配合Matlab軟件進行相關的編程計算,可求得相關插值姿態。
解算過程如下:
2)得到空間圓弧方程:
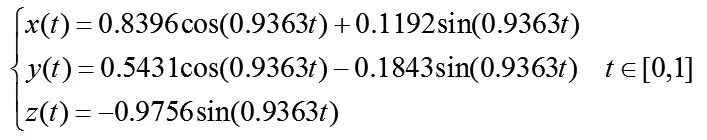
3)t在區間內按間隔為0.01均勻取100個值,得到空間圓弧上100個點的向量。
4)每個點的向量寫成純四元數,并與起始點進行上述相關運算,最后得到均勻插補姿態。
圖3為本算例對應的插補姿態圖,從圖中可以看出,姿態轉角平滑,變化均勻,無沖擊,有利于機械臂使用壽命。圖4為姿態轉角對應到繞X/Y/X軸轉動的歐拉角,從圖中可以看出繞X/Y/Z軸的轉角是線性變化的,各軸轉速基本保持定值,勻速平穩轉動,說明姿態插值合理可行。

圖3

圖4
4.結束語
用單位球面上的圓弧及向量表達四元數,均勻分配圓弧上的點,通過圓弧上各點向量進行姿態四元數插值,得到的插值姿態平穩無沖擊,結果合理可行。該方法比較直接地展現了四元數插值姿態的合成過程,有助于進一步進行機械手姿態的相關研究。

