加權復合算子在Dirichlet空間上的有界性
林慶澤
(廣東工業大學應用數學學院,廣東 廣州 510520)
0 引言
當0<p<∞時,用Ap表示單位圓盤Δ上滿足
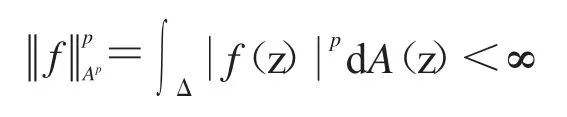
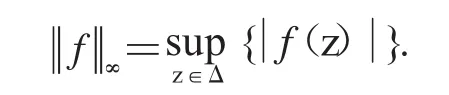
Dirichlet空間D(p0<p<∞)為f'屬于Bergman空間Ap的單位圓盤Δ上所有滿足的解析函數f組成的空間.
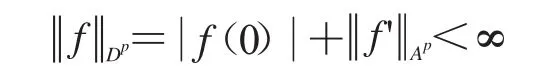
容易驗證,當1≤p<∞時,Dp是一個Banach空間.記H(Δ)表示單位圓盤Δ上所有解析函數組成的函數空間.若φ,φ,f∈H(Δ)且φ(Δ)?Δ,則定義加權復合算子為
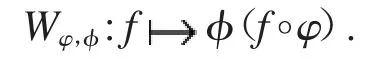
近年來,關于加權復合算子Wφ,φ作用在不同的函數空間上的研究是一個熱門的研究課題.文獻[1-2]得到了加權復合算子Wφ,φ作用在Hardy空間上有界性等性質.文獻[3-4]給出了Wφ,φ作用在不同加權Bergman空間之間和不同Hardy空間之間的有界性和緊性等性質的刻畫.另外,文獻[5-7]還研究了加權復合算子Wφ,φ作用在Bloch型空間上的有界性、緊性和本性范數等性質.
關于加權復合算子的研究背景,最具代表性的成果是文獻[8]證明了Hardy空間H1上的線性等距變換都是加權復合算子,緊接著Forelli在文獻[9]中證明了當1≤p<∞,p≠2時,在Hardy空間Hp空間上也有相同的結論.文獻[10-11]證明了導數Hardy空間Sp和Dirichlet空間Dp上的線性等距變換也有類似的結論.在加權Bergman空間上,Kolaski在文獻[12-13]上得到了線性等距變換可以表示為加權復合算子的相似結論.
對于加權復合算子Wφ,φ,如果令φ(z)=z,便得到了乘法算子Mφ:fφf;如果φ≡1,則得到復合算子Cφ:ff φ.近幾十年,這兩種算子在不同的函數空間上的有界性和緊性等性質的研究也是一個熱門的研究課題,可參考文獻[14-16].而在導數Hardy空間Sp上的復合算子的研究則開始于Roan的文獻[17].隨后,MacCluer在文獻[18]中用Carleson測度刻畫了Sp空間上的復合算子的有界性和緊性.Contreras和Hernandez-Diaz[19]將導數Hardy空間Sp上的加權復合算子的有界性和緊性的研究轉化為研究Hp空間上的加權復合算子的有界性和緊性.受文獻[19]思路的啟發,Kumar[20]利用Carleson測度[21]將Dirichlet空間Dp上的加權復合算子的有界性和緊性的研究轉化為研究Ap空間上的加權復合算子的有界性和緊性.
受文獻[22]的啟發,當2<q≤p<∞時,本文給出了Dp空間中元素的基于有限零點的分解并得到了當φ是Δ上的共形滿射時Dirichlet空間Dp到Dq上加權復合算子Wφ,φ的有界性的充要條件:Wφ,φ在Dp到Dq空間上是有界的當且僅當φ∈Dq.而作者與其他合作者關于加權復合算子Wφ,φ在導數Hardy空間Sp上的有界性的類似成果可參考文獻[23].
1 加權復合算子Wφ,φ在Dirichlet空間Dp上的有界性
下面命題1的證明思路參考于文獻[24-25]:
命題1若2<p<∞,則對于任意的f∈Dp,,從而Dp?H∞.
證明 若f∈Dp,則由定義f'∈Ap.由文獻[26-27]我們有
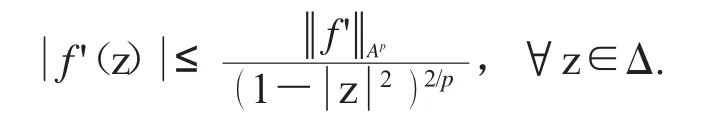
因此,
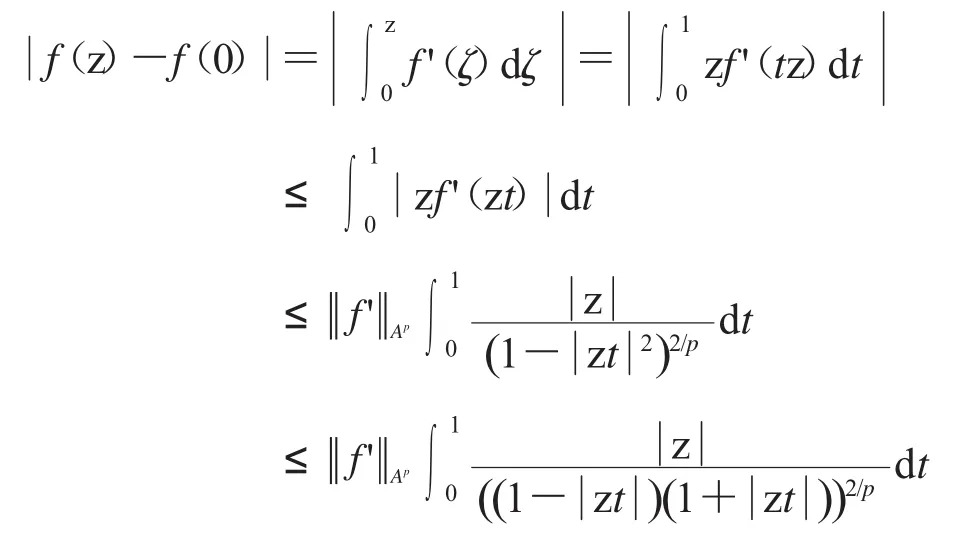
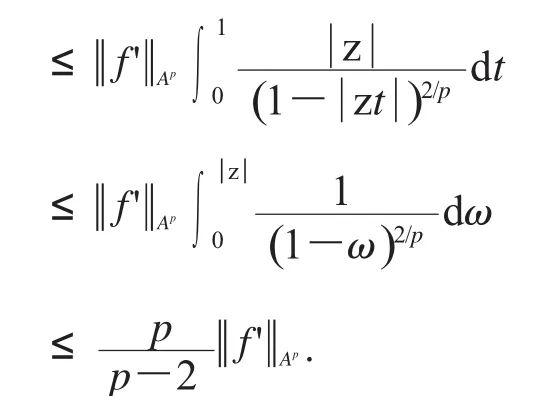
從而,
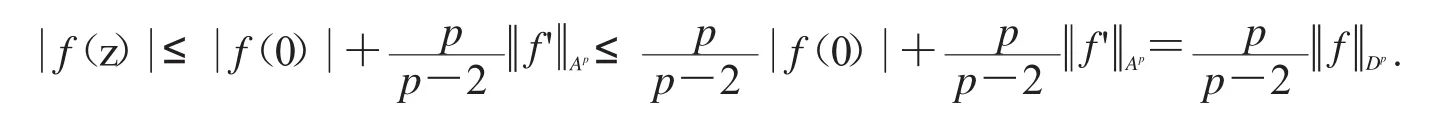
證畢.
下面的引理可參考文獻[27]:
引理1若φ是Δ上的解析函數且φ(Δ)?Δ,p>0,則對于?f∈Ap,都有
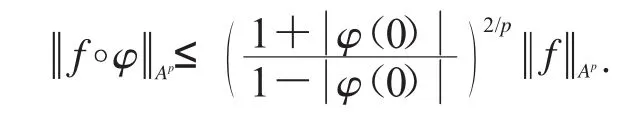
我們證明下面的命題.
命題2若2<p<∞,當φ是Δ上的共形滿射,f,g∈Dp時,以下結論成立:
(1)φ'∈H∞;
(2)存在某個與p和 φ 有關的常數cp,φ>0,使得;
證明(1)由復分析可知,φ是Δ上的共形滿射當且僅當存在某個a∈Δ以及單位模復數 ,使得
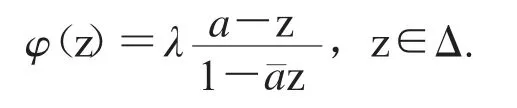
從而
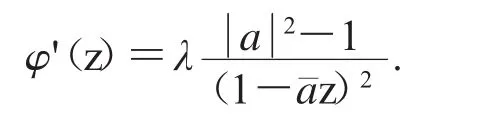
(2)由命題1,我們有
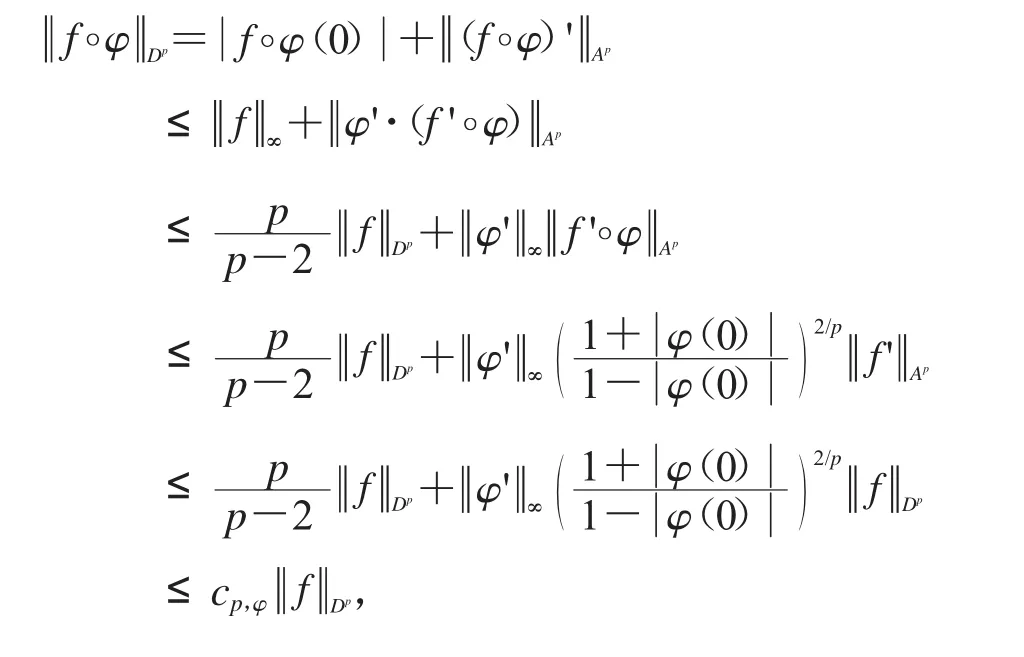
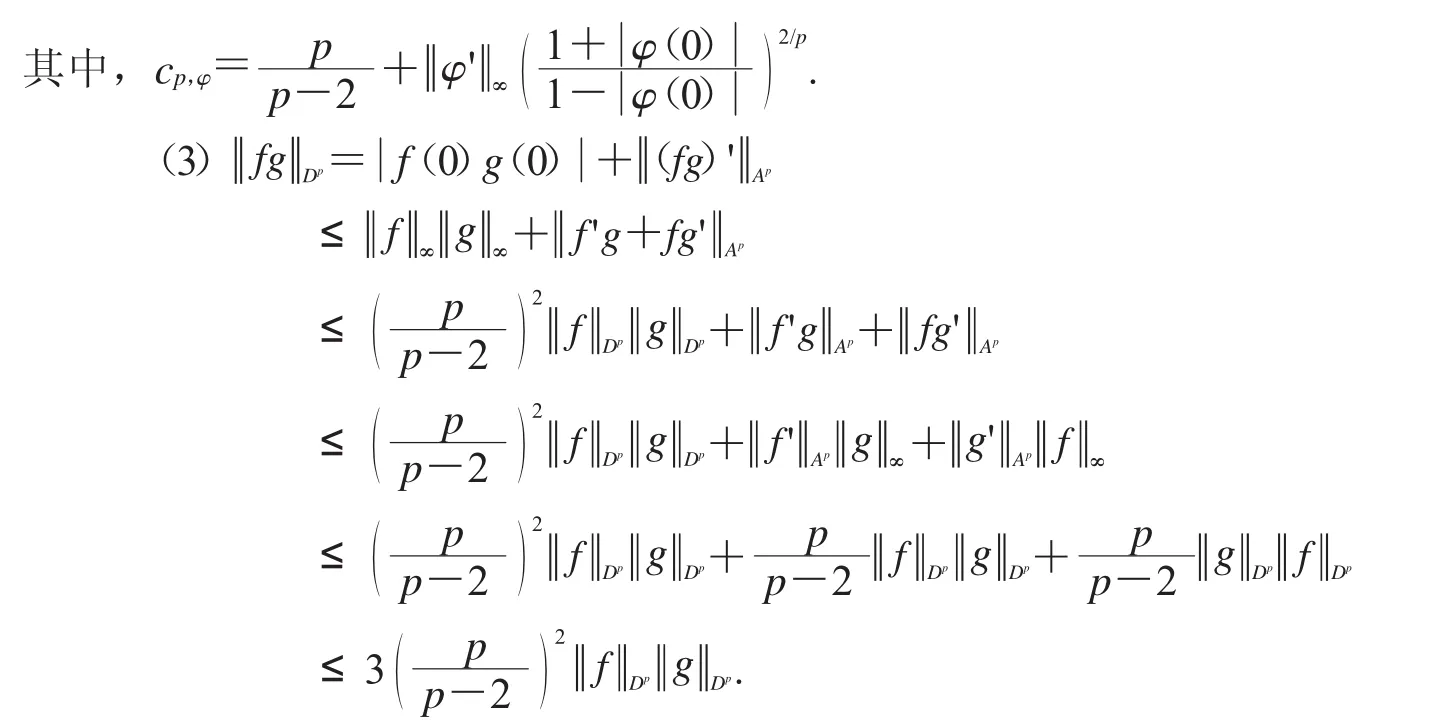
證畢.
由命題2中(3)可推出,若2<p<∞,則Dp對于函數的乘法運算構成一個Banach代數.
下面給出Dp空間中元素的基于有限零點的分解.
命題3若2<p<∞,f∈Dp,而ζ∈Δ是f的n階零點,那么存在g∈Dp,使得g(ζ)≠0 且 f(z)=(z-ζ)ng(z),z∈Δ.
證明 由 ζ∈Δ 是 f的 n階零點,故存在 g∈H(Δ),使得 g(ζ)≠0且 f(z)=(z-ζ)n·g(z),z∈Δ.下面證明 g∈Dp.
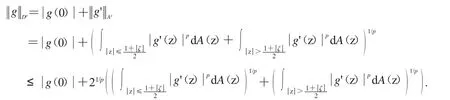
由于g∈H(Δ),上面不等式右邊第一個積分必定有界,現只需考慮第二個積分的上界.命題證畢.

推論1若2<p<∞,f∈Dp,而ζ1,ζ2,…,ζn∈Δ是f的零點(可以相同),那么存在g∈Dp,使得g(ζ)i≠0,i=1,2,…,n,且.
對于任意給定的z0∈Δ,若2<p<∞,由可知,線性泛函作用在D(p2<p<∞)空間上是有界的.下面的推論給出了線性泛函Ez0與算子Mz-z0作用在Dp空間上的聯系.
推論2若2<p<∞,當線性泛函Ez0與算子Mz-z0作用在Dp空間上時,有:
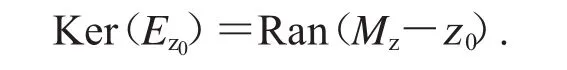
證明 對于任意的f∈Ke(rEz0),由命題3,存在g∈Dp使得f(z)=(z-z0)g(z),z∈Δ,即 f∈Ran(Mz-z0).反過來則是顯然的.證畢.
下面給出當φ是Δ上的共形滿射時加權復合算子Wφ,φ在Dp空間上的有界性的充要條件.
定理1當2<q≤p<∞時,若φ,φ∈H(Δ),φ(Δ)?Δ,且φ是Δ上的共形滿射,則加權復合算子Wφ,φ在Dp到Dq空間上是有界的當且僅當φ∈Dq.
證明 若Wφ,φ是有界的,則取f=1,由
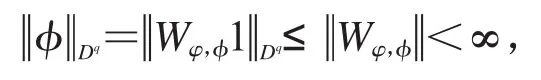
可知φ∈Dq.
現假設φ∈Dq,則由命題2,有
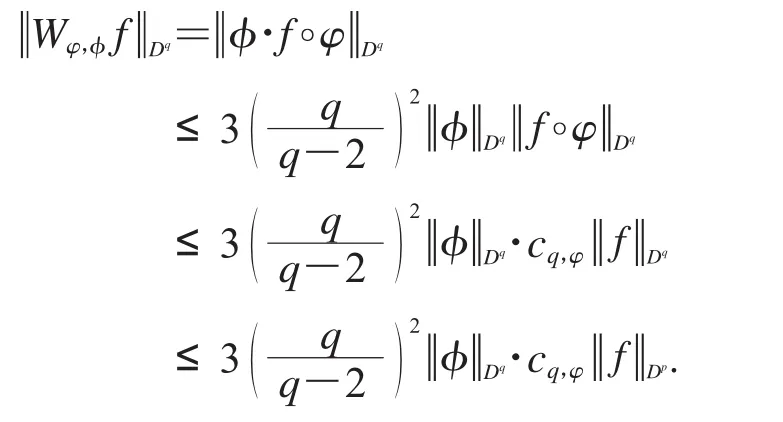
亦即Wφ,φ在Dp到Dq空間上是有界的.證畢.
當取φ(z)=z,z∈Δ時,由定理1,我們得到了關于乘法算子Mφ在Dp到Dq空間上有界性的充分必要條件:
推論3當2<q≤p<∞時,若φ∈H(Δ),則乘法算子Mφ在Dp到Dq空間上是有界的當且僅當φ∈Dq.
注1文獻[28]證明了當0<q<p<∞時,若φ∈H(Δ),則乘法算子Mφ在Dp到Dq空間上是有界的當且僅當φ≡0.

