CT系統參數標定及成像

謝睿誠，劉楚欣，潘玉媚，李 健

（汕頭大學理學院數學系，廣東 汕頭 515063）

0 引言

CT，即計算機斷層成像技術，是一種依據外部投影數據重建物體內部結構圖像的無損檢測技術.CT系統示意圖見圖1.

王召巴[1]在2001年從濾波反投影算法的基本原理著手，分析了CT系統旋轉中心偏移對圖像重構所造成的影響；Olander等[2]利用Radon變換性質把角度相差180°的投影經過平移與翻轉，計算出旋轉中心的偏移量；李增云等[3]再次證明了物體質心與其投影質心關系定理，并提出了利用部分投影快速校正CT系統旋轉中心的方法.這些方法理論上可以準確地確定CT系統旋轉中心的位置再進一步進行圖像的重構，但現實中往往因為其計算復雜，實操性不強等原因而難以在醫學和工業方面被廣泛應用.

由于CT系統對系統旋轉中心在托盤中的位置、探測器單元之間的距離以及X射線的180個方向等參數有極高的要求，這極大地增加了CT系統制造和安裝的難度.本文運用濾波反投影和Radon變換等，針對CT系統參數標定及成像展開研究.

1）建立了直接求解模型，求解CT系統旋轉中心在正方形托盤中的位置、探測器單元之間的距離以及該CT系統使用的X射線的180個方向，然后利用重構法驗證其結果.

2）建立濾波反投影模型計算未知介質的衰減系數，然后通過Radon變換和Beer-Lambert定律導出吸收率的計算公式，并由此計算未知介質吸收率.并根據此前確定的標定參數對吸收率數據進行校正，得出指定位置的吸收率，并重構出未知介質的圖像.

3）定義模板標定參數與實際參數的誤差為精度度量指標，定義重構前后吸收率的變化為穩定性度量指標.然后以矩形和正方形代替橢圓和圓建立新的標定模板，減少濾波反投影中插值方法產生的誤差.最后，通過對比兩個模板重構前后吸收率差距和重構前后吸收率變化量，認為方形模板的精度和穩定性比橢圓形模板更好.

本文的原文獲得2017年全國大學生數學建模競賽一等獎，所采用的數據亦來自2017年全國大學生數學建模競賽（http://www.mcm.edu.cn/html_cn/node/460baf68ab0ed0e1e 557a0c79b1c4648.html）.

1 問題提出

1.1 問題提出

問題1：在正方形托盤上放置兩個均勻固體介質組成的標定模板，模板的幾何信息如圖2所示，其中每一點的數值反映了該點的吸收強度，這里稱為“吸收率”.根據這一模板及其接收信息，確定CT系統旋轉中心在正方形托盤中的位置，探測器單元之間的距離以及該CT系統使用的X射線的180個方向.

問題2：附件3是利用上述CT系統得到的某未知介質的接收信息.利用問題1中得到的標定參數，確定該未知介質在正方形托盤中的位置，幾何形狀和吸收率等信息.另外，請具體給出圖3所給的10個位置處的吸收率.

問題3：附件5是利用上述CT系統得到的另一個未知介質的接收信息.利用問題1中得到的標定參數，給出該未知介質的相關信息.另外，請具體給出圖3所給的10個位置處的吸收率.

問題4：分析問題1中參數標定的精度和穩定性.在此基礎上自行設計新模板，建立對應的標定模型，以改進標定精度和穩定性.

圖1 CT系統示意圖

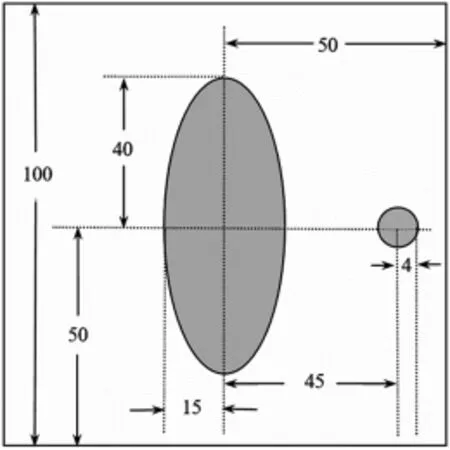
圖2 模板示意圖（mm）

圖3 10個位置示意圖

2 CT圖像重構模型推導

2.1 Radon變換和吸收率

根據文獻[4]，附件3中的接受信息數據即Radon變換的投影函數值，問題2、3是要求根據投影函數值來求吸收率，我們以衰減系數為橋梁構建投影函數值與吸收率之間的關系.Radon變換示意圖見圖4.

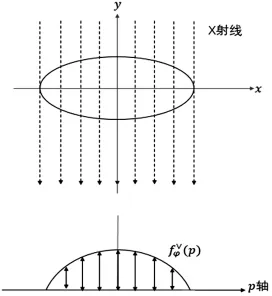
圖4 Radon變換示意圖

2.1.1 Radon變換（投影函數值與衰減系數的關系）

設p軸與X射線垂直，p＝xcosφ＋ysinφ.設未知介質的函數為f（x，y），未知介質經X射線投影在p軸上得到，即：

上述是Radon變換的原理，但在這個問題中，我們已知的數據是附件3中的接收信息數據即Radon變換的投影函數值，要通過來求 f（x，y）的函數值，得出物質的吸收率來畫出物質的圖像，因此本問題可以轉換為求Radon變換的逆過程，根據文獻[4]，這個過程就是圖像重構的過程，我們將采取濾波反投影的方法來得到f（x，y）.

2.1.2 Beer-Lambert定律（衰減系數轉換為吸收率）

由Beer-Lambert定律[8]可知：

其中，A為物體的吸光率，K為吸收率（對于某種均勻的物質，K為常數），l為介質厚度，c為吸光物質濃度（對均勻物體，c為常數）.

設μ為衰減系數，令

即衰減系數和吸收率之間的關系是線性關系.

據公式（1）和公式（4）有：

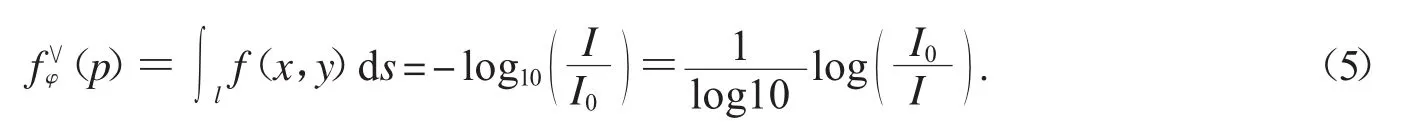
因此可以根據物體在不同角度下X射線的接收信息利用濾波反投影原理來重構物體.

2.2 濾波反投影原理

2.2.1 投影切片定律：

F（ωcosφ，ωsinφ）見 2.1和 2.2.2中說明.

2.2.2 二維傅里葉變換及極坐標變換：

定義

為f（x，y）的二維傅里葉變換.

令 u＝ωcosφ，v＝ωsinφ，則有函數

式中G（φω）為通過φ角的F切片，對固定的φ，G（φω）只有一個自變量.

那么上式可以表示為：

2.2.3 濾波器（文獻[5]）：

根據傅里葉變換的卷積定理：

2.2.4 傅里葉逆變換

但我們運用上式的離散化形式：

2.3 濾波反投影原理在本題中的應用

濾波反重構原理要應用于本題重構過程中，還需要解決下面兩個問題：插值方法的選擇和濾波器的選擇.

2.3.1 插值方法的選擇

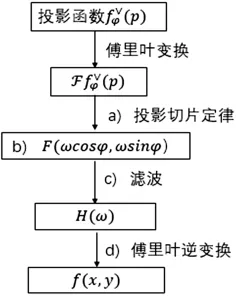
圖5 濾波反投影步驟圖

a）線性插值

線性插值中插值點xi，i＝1，2，…，511對應的投影函數的計算公式如下所示：

b）三次樣條插值

三次樣條插值法中插值點 xi，i＝1，2，…，511對應的投影函數的計算公式如下所示：

其中ai，bi，ci，di為參數，由確定.

2.3.2 濾波器的選擇

我們選擇的濾波器是Cosine濾波器，Cosine濾波器是在Ram-Lak濾波器的基礎上乘上一個Cosine函數.

Ram-Lak濾波器：

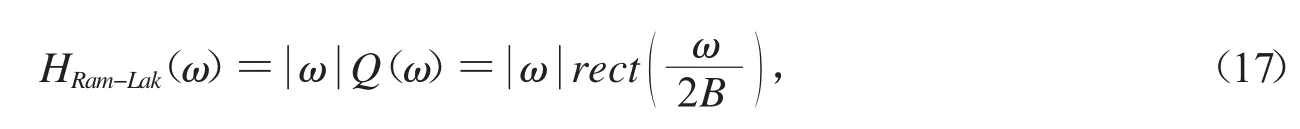
3 問題1模型的建立與求解

3.1 確定探測器單元之間的距離d

探測器單元之間的距離d，可理解為探測器單元數密度的倒數，即該問題可通過求解探測器單元數密度來解決.

a）根據附件提供的第151次旋轉數據，光源平行于y軸時，接收到信息的探測器單元個數n為108個.結合模板的幾何信息可知，108個探測器單元個數對應的實際距離l為30 mm，即探測器單元數密度ρ為：

b）根據附件中第61次旋轉的數據，光源平行于x軸時，接收到信息的探測器單位個數為288個.圖2模板示意圖提供的長軸長度為80 mm，類似地，根據a）可求出探測器單位數密度同樣為3.6個/mm，探測器單元之間的距離d為0.277 8 mm.

經以上分析可得探測器單元之間的距離為0.277 8 mm.

3.2 確定CT系統使用的X射線的180個方向

利用重構原理（詳見2.1 Radon變換和吸收率），將附件2數據進行重構圖像，得到的重構圖像如圖6所示：

觀察圖6發現，附件2數據重構圖像發生了明顯的角度偏轉.利用橢圓與圓圓心連線與水平方向的夾角即重構所得圖像的偏轉角度為29.649 3°.因此，掃描光源初始方向為與x軸負半軸夾角為60.350 7°，從第四象限指向第二象限的方向，掃描光源最終方向為初始方向的逆方向，每次CT系統逆時針旋轉1°.

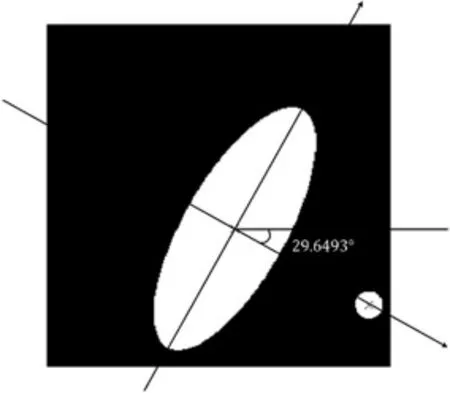
圖6 附件2數據重構得到的圖像

3.3 求解CT系統旋轉中心

利用3.2中得到的初始旋轉角度，對重構圖像進行修正結果如圖7所示.

由于橢圓模板在標定時放置在托盤的正中央，其重構圖像也應該在正中央，可是圖像中橢圓形的中心與圖像中心并不重合，因而可以利用橢圓中心與圖像中心的偏差來確定CT系統的旋轉中心.

以重構圖像的橢圓圓心為原點，建立圖8所示坐標系，圖像中心位于直角坐標坐標系的第二象限，求得圖像中心的位置為（-8.998 5，5.999 1）.

圖7 調整角度后重構得到的圖像

圖8 置于坐標系的重構圖像

4 問題2，3模型的建立與求解

4.1 吸收率校正模型

利用濾波反投影原理對標定模板的180個角度的接收信息進行重構，并利用3.2和3.3中所得角度和旋轉中心位置，對重構圖像的方向和位置進行校正.可得圖像標定模板中吸收率為1.000 0處的衰減系數的觀測值中位數為0.490 4，標定模板中吸收率為0.000 0處的吸收率中位數為0.000 1.由Beer-Lambert定律，可以得吸收率與衰減系數關系為：

4.2 問題2圖像重構

依據2中建立的模型，利用濾波反投影原理對附件3所給的接收信息進行重構，并利用公式（21）進行校正，得到重構圖像如圖9所示，問題中指定的10個位置處的吸收率結果如表1所示.

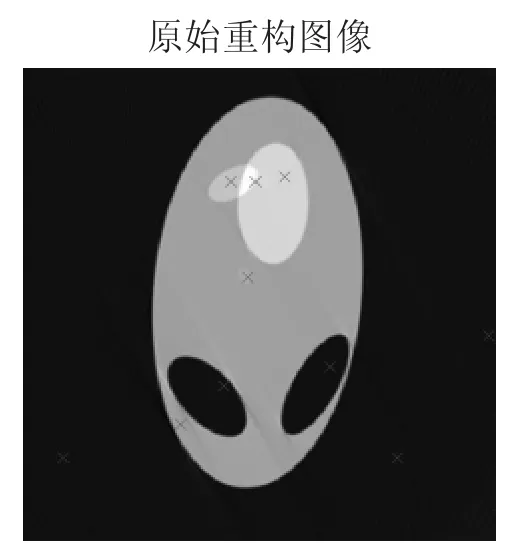
圖9 原始重構圖像（標記指定位置）

表1 圖9所給10個位置處的吸收率結果

4.3 問題3圖像重構

利用2中建立的模型，根據濾波反投影模型將CT系統得到的未知介質接收信息，即附件5數據進行圖像重構，并利用公式（21）進行優化，得到的重構圖像如圖10所示，問題指定的10個位置處的吸收率結果如表2所示.

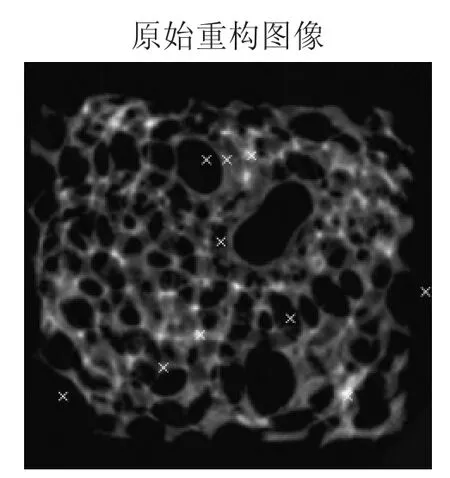
圖10 原始重構圖像（標記指定位置）

表2 圖3所給10個位置處的吸收率結果

5 問題4模型的建立與求解

5.1 模型的建立

5.1.1 精度評價

1）模板位置對校正精度的影響

通過平移，旋轉變換，改變模板的位置并對模板做Radon變換，得到模板的接收信息，并利用3中確定旋轉中心和初始投影角度的方法，求解旋轉中心和初始投影角度.與實際位置進行比較，重復多次并求平均值，得到平均誤差作為精度估計依據.

2）Radon變換再重構的吸收率差距

對模板作Radon變換得出模板的投影數據，再用投影數據運用2中建立的重構方法還原圖像，在模板和重構得到的圖像中建立相同的坐標系，比較相同坐標下兩者的吸收率數值差距，設前者為fo（x，y），后者為fl（x，y）.

用L2范數來衡量fo（x，y）和fl（x，y）之間的差距R，設已知吸收率的點構成m×m的矩陣：

用均方誤差來衡量吸收率的差距大小，均方誤差計算公式為：

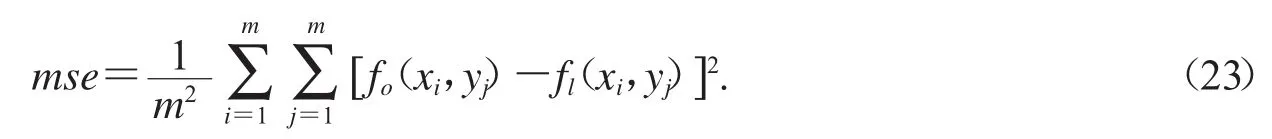
5.1.2 穩定性評價

我們用各參數對精度的影響來衡量模板的穩定性，在兩種模板的精度足夠好的情況下，通過改變反投影方向數、旋轉中心平移距離、初始旋轉角度大小以及計算精度指標中的重構前后吸收率差距的變化量來說明其穩定性，即吸收率差距變化不大就認為模板的參數標定精度穩定，反之則不穩定.

5.2 新標定模板設計

5.2.1 原始標定模板誤差成因分析

a）角度變化引起的探測器數目變化量

附件2中被判斷為X射線掃描光源方向平行于x軸的數據有7組，即第58次掃描至第64次掃描得到的接收信息的探測器單元個數相同.考慮造成這樣現象的原因是當X射線掃描光源方向旋轉至與x軸夾角較小的區域內時，每逆時針旋轉一次引起標定模板投影的接收數據變化量極小，且CT系統測量的精度不高，不足以反映出如此微小的變化量.

b）插值方法的適應性

由于重構方法中應用的是線性插值方法，橢圓的邊緣為圓弧狀，線性插值并不能完全貼合橢圓邊緣，在線性插值中會引起誤差.即使用其它插值方法如多項式插值方法也不可以完全貼合，因此原始模板會在重構圖形時產生誤差.

5.2.2 新模板設計

針對原始模板的不足之處，我們構建新的模板（方形模板）如圖11所示：

圖11 新模板示意圖

圖12 新模板吸收率

如圖11所示，新模板（方形模板）由矩形和正方形組成，矩形中心在正方形托盤的中心，矩形和正方形均關于正方形托盤的水平對稱軸對稱，其幾何信息如圖11所示.

5.3 模板測試

我們對橢圓模板（原始模板）以及方形模板（新模板）做Radon變換以及重構，并進行精度分析和穩定性分析.

5.3.1 精確度評價對比

對橢圓模板和方形模板做20次不同的平移變換和30次不同角度的旋轉變化，并計算坐標和旋轉角度與實際值的平均誤差（見表3）.

表3 橢圓模板和方形模板的校正精度對比

從表3可以看出，橢圓模板和方形模板的標定參數的誤差都比較小，精度較高，因而兩個模板都適合參數標定.

5.3.2 穩定性評價對比

由于CT系統是以等角度間隔掃描一次方式離散進行的，我們定義CT系統掃描1周所做投影的數量，也即重構圖像時可以利用的輪廓數量為反投影方向數.為探究在反投影方向數減少，投影方向的角度間隔增大時，兩種模板的穩定性.以反投影方向數為橫坐標，以模板原吸收率與重構后模板吸收率的歐幾里得距離和均方誤差為縱坐標，建立平面直角坐標以呈現橢圓模板和方形模板在吸收率差距這一精確度指標上的差別.

由圖13和圖14可以看出，在反投影方向數范圍為（0，180]時，方形模板與橢圓模板相比，重構前后吸收率差距都比較小，并且在減少反投影方向數時，方形模板吸收率差距的變化量比橢圓模板的要小，這說明方形模板的穩定性比橢圓模板的要高.

進一步探究模板擺放時旋轉中心位置及旋轉角度對精度的影響，分別以旋轉中心平移距離和旋轉角度為橫坐標，以模板原吸收率與重構后模板吸收率的歐氏距離為縱坐標，建立平面直角坐標系得到圖15，圖16（平移距離）以及圖17圖18（旋轉坐標），橢圓模板和方形模板在穩定性指標上的差別見圖15-圖18.

由圖15圖16可以看出，在調節旋轉中心的位置變化時，橢圓模板的誤差要稍小于方形模板，并且二者的誤差都很小（mse＜0.001），很難區分方形模板與橢圓模板的精度和穩定性差距.進一步的，從旋轉角度變化的影響來探究（見圖17圖18）橢圓模板和方形模板的差距.

圖13 不同反投影方向數下兩種模板重構前后吸收率差距對比（以歐幾里得距離衡量）

圖14 不同反投影方向數下兩種模板重構前后吸收率差距對比（以均方誤差衡量）

圖15 不同平移距離下兩種模板重構前后吸收率差距對比（以歐幾里得距離衡量）

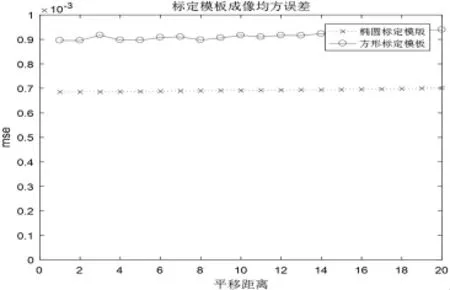
圖16 不同平移距離下兩種模板重構前后吸收率差距對比（以均方誤差衡量）

圖17 不同旋轉角度下兩種模板重構前后吸收率差距對比（以歐幾里得距離衡量）

圖18 不同旋轉角度下兩種模板重構前后吸收率差距對比（以均方誤差衡量）

由圖17和圖18可以看出，在改變旋轉角度（橫坐標）時，在旋轉角度大于10°時，方形模板重構前后的吸收率差距比橢圓模板的小，并且在旋轉角度小于10°時，二者誤差都很小，因而認為模板的擺放角度對標定精度影響不大.

綜上所述，改變反投影方向數時，方形模板的穩定性優于橢圓模板；平移，旋轉時方形模板和橢圓模板重構的誤差都極小.故使用方形模板作為標定模板要優于橢圓模板.

6 模型評價

本文建立的濾波反投影模型實現簡單，精度高，運算量小，能獲得較好的重建圖像，對實際生產中的CT系統參數的修正有一定的幫助，但重構所得圖像邊緣出現偽影，雖然我們使用的中值濾波有效平滑去除圖像的噪聲點，但未能完全消除其影響，這也是后續深入研究的一個方向.