基于改進人工魚群算法的回歸模型參數估計

于卓熙，靳雨佳

（1.吉林財經大學 管理科學與信息工程學院；2.吉林省互聯網金融重點實驗室，長春 130117）

0 引言

多元線性回歸分析[1]是一種重要的數據分析方法，廣泛應用于工業、農業、醫學、社會調查、生物信息處理等領域。多元線性回歸分析的重點是參數估計問題。如今，解決參數估計問題最常用的方法是最小二乘法，但是由于該方法的計算過程復雜且程序不具有通用性，對于結構復雜、規模較大等特征的數據具有一定的局限性。近些年，隨著遺傳算法、群智能技術的飛速發展，將智能優化算法應用于回歸模型的參數估計已經越來越受到歡迎。劉錦萍等[2]應用改進的粒子群算法對多元線性回歸模型進行參數估計，通過測試實驗表明，估計結果顯著提高；楊兆軍，楊川貴等[3]將粒子群算法和支持向量機結合，應用于回歸模型的參數估計研究；張姣玲等[4]應用人工蜂群算法估計多元線性回歸參數；彭宇文,郭莉莎等[5]將改進的模擬退火算法應用于線性和非線性回歸模型的參數估計。然而，遺傳算法在編碼和解碼環節復雜繁瑣，在處理復雜數據時優化效率會降低；粒子群優化算法往往會由于初始化參數設定問題，使算法在尋優過程中易陷入局部最優解，而搜索不到全局最優解。

針對人工魚群算法在尋優過程中獲取精確解方面存在不足，本文通過對人工魚群算法的參數和魚群行為進行改進，將改進的人工魚群算法應用于回歸模型的參數估計中,并通過對比實驗，表明改進的算法有效、實用且簡單。

1 模型與算法介紹

1.1 多元線性回歸模型

在多元線性回歸分析中,對隨機變量y進行預測時,往往有多個因素影響著其未來值的變化，當 y與x1，x2，…，xn(n≥1)之間基本存在線性關系時，需要用多元線性回歸法進行預測。在n個自變量的情況下,多元線性回歸模型為：

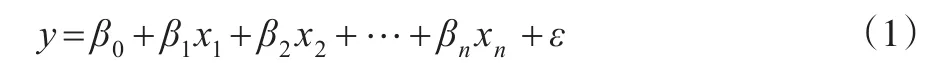
其中，β0，β1，β2，…，βn是 n+1個待估參數。

1.2 人工魚群算法

人工魚群算法[6](Artificial Fish-swarm Algorithm，AFSA)是李曉磊等通過長期觀察魚的活動規律及特點，提出的動物自治體優化方法，它是一種群智能的高效尋優方法。

人工魚群的狀態可以用向量 Xi=(x1，x2，...，xn)表示，其中 xi(i=1，2，3，...，n)表示欲尋優變量；人工魚當前所在位置的食物濃度表示為Y=f(Xi)，其中Y為目標函數；人工魚個體之間的距離表示為；Visual表示人工魚的感知范圍；Step表示人工魚移動的步長；δ表示擁擠因子。人工魚群算法的基本思想是選擇部分人工魚完成初始化操作，通過覓食行為、聚群行為和追尾行為不斷更新自己，以迭代的方式尋找最優解。

2 改進的人工魚群算法

2.1 算法參數的改進

本文引入內核函數對人工魚的視野和步長進行自適應調整[7]，無需對算法整體做大規模變動。具體方法是應用內核函數對時間參數進行調整，分別帶入到下面視野和步長的函數中，對它們做動態性調整。

其中，Visualmax為最大視野，Stepmax為最大步長。設定算法運行初期人工魚的視野和步長最大，使算法在運行初期能夠快速收斂，突破局部極值的限制。算法在運行過程中，K(x)逐漸減小，直到趨于零，此時，視野和步長均為最小值，使算法在運行后期能夠獲取到全局精確解。

2.2 聚群行為的改進

對魚群的聚群行為進行改進[8]，設定Xi(t)為魚群的當前狀態，第i條人工魚代表一個可行解向量Xi，Xi=，nf為人工魚視野內的同伴數量，Xc(t)表示魚群的中心位置。若f(Xc(t))·nf＜δ·f(Xi(t))，則意味著人工魚鄰域內同伴魚群中心食物濃度較高且擁擠度較低，人工魚向全局最優位置Xbest和伙伴的中心位置的向量和的方向前進一個步長；若f(Xc(t))·nf＞δ·f(Xi(t))，則人工魚執行覓食行為，表達式如下所示：

2.3 人工魚個體與適應度函數定義

利用改進的人工魚群算法進行多元線性回歸參數估計[9]。把多元線性回歸模型中的一組參數看作一條人工魚,種群中的每一條人工魚代表模型估計問題中的一個候選解,第i條人工魚Xi表示為

應用適應度函數來評價種群中的每條人工魚，定義如下：

對適應度函數求極值，可以得到一組參數估計量，即為最優解。

2.4 改進的人工魚群算法步驟

應用改進的人工魚群算法進行參數估計的主要步驟流程圖如圖1所示[10]：

圖1 改進的人工魚群算法流程圖

3 仿真實驗及結果分析

為了驗證本文提出的改進的人工魚群算法在多元線性回歸模型參數估計中的應用，選取了表1中所示的數據，已知變量y，受變量x1，x2和R2的影響，建立多元線性回歸模型如下：

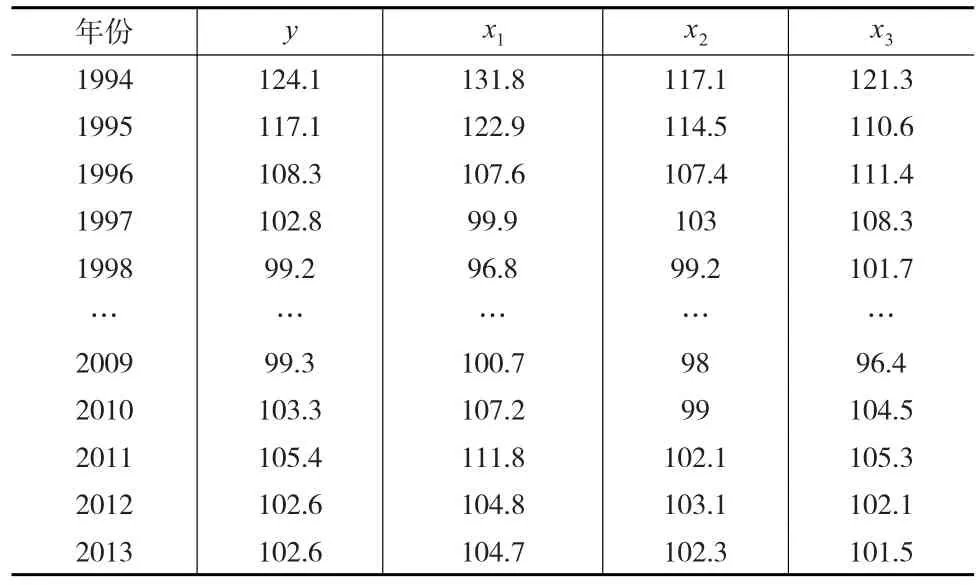
表1 參數估計的數據

表2是改進的人工魚群算法，人工魚群算法和最小二乘法進行參數估計的對比結果，包括線性回歸模型的參數估計值，殘差平方和，最優解和運行時間。

表2 算法參數估計對比結果

從表2可以看出，應用改進的人工魚群算法進行參數估計的結果優于人工魚群算法和最小二乘法的結果，而且在尋找最優值上有所提高，加快了運行時間。

應用人工魚群算法和改進的人工魚群算法得到的一次典型實驗曲線分別如圖2和圖3所示。

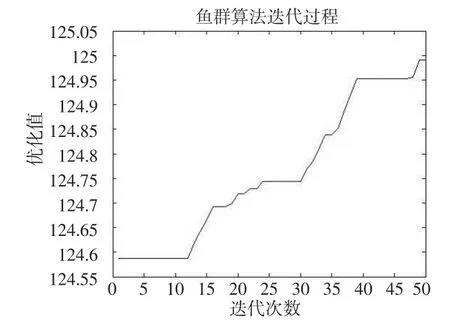
圖2 人工魚群算法的典型實驗曲線

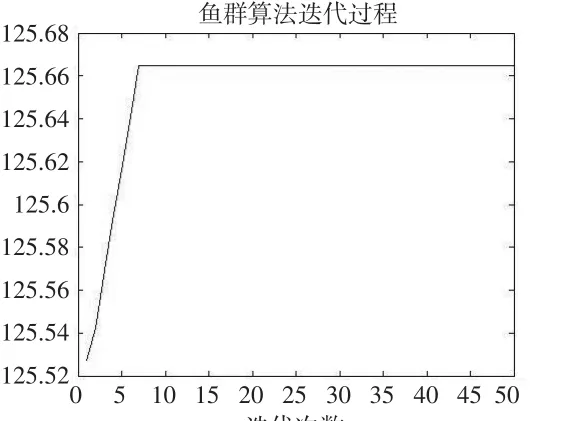
圖3 改進的人工魚群算法的典型實驗曲線

從圖2和圖3的對比來看，使用人工魚群算法進行參數估計時在124.588處陷入到局部最優解。然而，改進的人工魚群算法能夠突破局部極值，搜索到全局最優解。

4 結束語

針對人工魚群算法在獲取精確解時的局限性，本文首先對算法參數做出了改進，并利用改進的人工魚群算法對多元線性回歸模型的參數進行了估計，通過與人工魚群算法和最小二乘法的參數估計結果進行對比，應用改進的人工魚群算法得到的參數估計結果和運行時間都有所提高，而且改進的算法運行時間短這一優勢會隨著參數個數的增加而越發明顯，可以將此方法推廣到對一般回歸模型的參數估計中，本文提出的改進的人工魚群算法為回歸分析中參數估計問題提供了一種新的有效解決方法。