偏航工況下風力機尾流特性分析
周文平,賀元成
(1.六盤水師范學院電氣工程學院,貴州六盤水553004;2.瀘州職業技術學院,四川瀘州646005;3.四川理工大學機械工程學院,四川自貢643000)
0 引 言
風力機處于自然環境中,當風力機偏航運行時,旋轉周期內葉片附著環量會隨方位角變化,在葉片后緣拖出包含有尾隨渦和脫體渦的非穩態尾流區[1]。尾流區的存在會導致葉片承受周期變化的氣動載荷,加劇葉片的揮舞和擺振,甚至影響輸出功率的質量[2]。
在對風力機處于偏航工況下的尾流特性和氣動性能進行分析時,傳統的動量葉素理論(BEM)需要加入動態入流修正模型才能預測隨時間變化的渦尾跡結構和非定常氣動性能,而且計算精度較差[3]。 計算流體力學(CFD)數值模擬雖能較好地模擬葉片周圍的流動特性和氣動性能,但計算費時且受數值耗散等因素影響較多[4]。渦流理論基于不可壓縮和定常流動假設,能較準確的模擬尾跡結構,尤其是在風力機偏航運行時,能夠自動計入偏斜尾跡結構對風輪性能的影響[5- 6]。因此,考慮風力機偏航運行時尾流的復雜性,渦流理論是最適合的氣動性能分析方法。本文采用基于渦流理論的自由尾跡模型對風力機處于偏航工況下的尾渦結構進行計算,分析其對尾流特性及氣動性能的影響規律。
1 計算模型
1.1 葉片升力面模型

圖1 自由尾跡模型分析示意
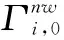
(1)
式中,ψ為葉片方位角;Δψ為方位角步長;i取0~Nr-1之間的值。
由Betz卷起理論[7],近尾跡區是不穩定的。假設近尾跡在轉過30°后聚合并卷起為單根葉尖渦,形成遠尾跡。以壽命角ξ表示遠尾跡的發展,并以步長Δξ將遠尾跡離散為有限個遠尾跡節點。初始葉尖渦的環量Γfw(ψ,0)等于上一時刻葉片上附著環量的最大值,即
(2)
葉片坐標系中,初始葉尖渦展向位置為
(3)
式中,Ri和Ro分別為葉根和葉尖半徑。
葉片渦格附著渦環量可通過求解控制點處物面不穿透條件方程得到[8],即
(4)
式中,Inm為升力面上第n個渦格對第m個渦格控制點的法向影響系數矩陣,假設葉片為剛性葉片,則該系數為常數,只需計算一次;Vm為近尾跡和遠尾跡在渦格控制點處的誘導速度,其值由自由尾跡模型計算得到;Wm為來流風速V∞與葉片微段旋轉速度的合速度;nm為渦格控制點的法向矢量。求解該線性方程組即可得到每個葉片渦格上附著渦的環量。
1.2 尾跡模型
尾跡模型將葉片后拖出的尾跡渦線以步長Δξ離散為有限個直線渦段,每個節點以當地速度在流場中自由運動。尾跡幾何控制方程為
(5)
式中,r為尾流場中節點的位置矢量;t為時間;V為節點速度,可表示為
(6)
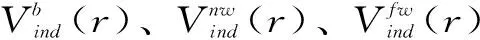
給出初始條件,對式(5)沿時間t積分,即可以得到尾跡形狀的時間歷程。考慮計算的準確性、穩定性和計算效率,對方程的求解采用一階歐拉顯式差分,即
r(ψ+Δψ,ξ+Δξ)=r(ψ,ξ)+V(ψ,ξ)Δψ/Ω
(7)
2 計算流程
自由尾跡計算過程如下:
(1)給定入流和葉片參數,由升力面模型生成葉片渦格和近尾跡渦系。
(2)由剛性尾跡模型[10]生成遠尾跡的葉尖渦系。
(3)由式(6)計算當前方位角時近、遠尾跡各節點的誘導速度。
(4)沿方位角步進Δψ,由式(3)、(7)計算ψ+Δψ方位角的尾跡形狀。
(5)由式(4)的物面不穿透條件計算該方位角時的渦格環量。
(6)由式(1)、(2)計算近尾跡區及葉尖渦環量。
(7)當計算方位角是2π的整數倍時進行收斂判斷。收斂則計算結束,否則進行下一步。
(8)重復步驟(3)繼續進行尾跡計算。
3 計算結果
計算對象為MEXICO的3葉片風力機[11]。該風力機葉片數為3,風輪半徑2.25 m,采用DU 91-W2-250、RIS? A1-21及NACA 64- 4183種翼型。計算來流風速14.99 m/s、轉速424.5 r/min、偏航角γ=30°時的尾渦結構和尾流特性。
3.1 葉尖渦位置
圖2給出了自由尾跡模型計算得到的葉尖渦位置,并與文獻[12]由實驗得到的前3圈葉尖渦位置進行比較。可以看出,盡管受來流風和自誘導的影響,尾跡結構擾動較明顯且呈現一定的卷起趨勢,但尾渦位置的計算值和實驗值取得了較好的一致,僅僅在第2、3圈尾跡的下風側低估了軸向位移。
對偏航工況時的尾渦結構進行分析時,尾跡偏斜角χ(即尾跡中心線與旋轉軸的夾角)是一個重要的參數。對圖2的葉尖渦結構進行分析可知,該工況下的尾跡偏斜角約為44°,大于偏航入流角γ,這與文獻[3]中的結論是一致的,表明自由尾跡模型是有效的。

圖2 30度偏航時葉尖渦位置
3.2 尾流區橫向速度分布
風力機尾流區的流動決定著葉片氣動載荷及下游風力機的入流情況。
圖3給出了槳盤平面的下游0.15 m處的軸向、切向及徑向速度分布。其中尾跡誘導速度表示由近尾跡及遠尾跡組成的尾跡渦的誘導速度分量之和,葉片誘導速度表示葉片附著渦的誘導速度分量,合速度由總誘導速度與來流風速相加得到。
從圖中可以看出,尾流速度沿風輪中心呈現不對稱分布,流動的非穩態特性較明顯。在y=±2 m附近有明顯的突變,這是由于葉尖渦的存在對周圍流動產生的影響導致的;風輪中心y=0 m附近處的速度突變則是由近尾跡區葉根附近的渦格引起的。
進一步分析渦系對尾流區的影響發現,葉片附著渦對尾跡區流動的影響主要在軸向和徑向方向,對切向流動的誘導影響較小;尾跡渦的誘導影響主要在切向和徑向方向,對軸向流動的誘導影響較小。從圖3b可以看出,尾跡渦對y軸負方向位置的切向誘導影響大于正方向位置的影響,導致尾跡渦整體往y軸負方向偏移,這也解釋了3.1節中得到的尾跡偏斜角大于偏航入流角的結論。從圖3c可以看出,偏航工況時,尾渦會在尾流區誘導出較大尺度的徑向流動。徑向流動的存在使得葉素之間存在較大的干擾,也會影響風力機的失速特性。因此,在將BEM理論用于偏航工況計算時,需要對二維流動假設及翼型氣動升阻力特性進行相應的修正。
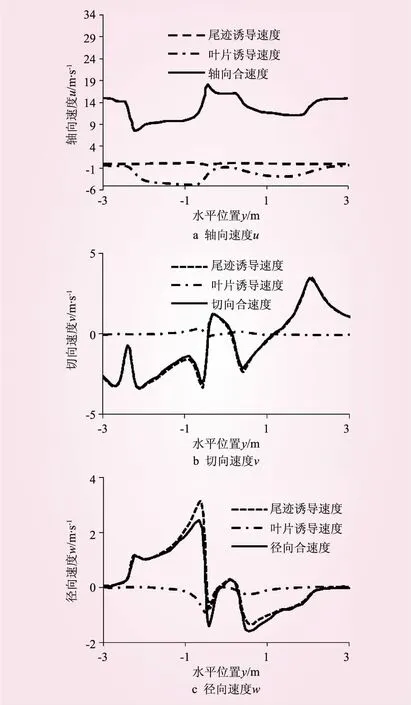
圖3 槳盤下游0.15 m處尾流速度分布
3.3 尾流區縱向速度分布
對圖2所示的尾流區內直線L1、L2上的氣流速度進行計算。L1和L2直線分別位于葉片上、下風側80%展向,與風輪旋轉軸呈30°夾角的位置上。
圖4給出了L1和L2直線上速度分布。可以看出,切向速度指向y軸負方向,沿L1直線逐漸增大,在槳盤下游約1 m達到最大值。此后,隨著L1直線進入尾流中心區域,葉尖渦的誘導影響減小,切向速度分量逐漸減小接近0。與切向速度不同,徑向速度隨著軸向距離的增加逐漸增加。
由于L2直線穿越上風側的葉尖渦區,且該區域的葉尖渦結構存在較大的擾動,因此流速的擾動也較大。L2直線穿出渦區后,徑向速度迅速降為0。
上述結果表明,在葉尖渦所圍成的尾流區內,流動以軸向流動和徑向流動為主;在尾流區外,流動以軸向流動和切向流動為主。

圖4 尾流速度軸向分布
4 結 論
結合升力面模型和基于渦流理論的自由尾跡模型研究對偏航未對準時風力機尾渦結構及流場特性進行分析,結果表明:
(1)風力機偏航運行時,尾渦呈現出非對稱的偏斜結構,且尾渦偏斜角大于偏航入流角。
(2)在尾流區內部,葉片附著渦對尾流區流動的
誘導影響主要在軸向和徑向方向,尾跡渦的誘導影響主要在切向和徑向方向。因此,偏航工況時,尾流區存在大尺度的徑向流動,會影響葉片的失速特性和升阻特性,在進行風力機設計及氣動性能計算時,需予以考慮。
(3)在尾流區內,流動以軸向流動和徑向流動為主;在尾流區外,流動以軸向流動和切向流動為主。這為風場內風力機的優化布置提供了理論指導。

