一種基于UPF的軸承剩余壽命預測方法

文 娟， 高宏力

(西南交通大學 機械工程學院 先進驅動節能技術教育部工程研究中心，成都 610031)

作為一種關鍵零部件，軸承被廣泛應用于各種機械系統中。通常軸承的工況復雜，工作環境惡劣，因而頻繁出現各種故障。一旦軸承出現故障，可能會造成整個機械系統停機，帶來災難。因此，適時監測軸承狀態，并根據狀態監測結果指導維修計劃對于提高系統可靠性與降低生產成本具有重要意義。狀態維修(Condition-Based Maintenance)主要包括兩個部分，故障診斷和故障預警[1-3]。故障診斷的主要任務為判斷系統能否正常工作，一旦不能工作，將會停機并更換故障零部件。故障預警的主要任務為判斷系統的當前狀態，并根據當前狀態對系統的剩余服役壽命進行預測，并使用預測結果指導維修計劃的制定。準確的故障預警能夠在確保安全的情況下節約維修費用，因而受到了越來越多研究者的關注。

通常壽命預測可以分為兩種，基于數據驅動的方法和基于模型的方法。數據驅動的方法試圖通過機器學習方法建立狀態監測數據與系統退化過程之間的關系。Tian等[4]提出了一種利用失效數據和未失效懸疑數據建立人工神經網絡(Articial Neural Network)壽命預測模型的方法。Tran等[5]利用時間序列技術和支持向量機(Support Vector Machines)對剩余壽命進行預測。與數據驅動方法不同，基于模型的方法主要通過建立能夠反應退化過程的數學模型來對剩余壽命進行預測。Gebraeel等[6-8]在數學模型的建立方面完成了許多工作。模型建立后，通常需要利用貝葉斯推斷理論結合狀態監測數據估計系統狀態和模型參數，并完成壽命預測。

傳統的實現貝葉斯推斷的方法有卡爾曼濾波(Kalman filter, KF)和擴展卡爾曼濾波(Extended Kalman filter, EKF)，都已成功應用到壽命預測中[9]。粒子濾波(Particle filter, PF)是一種利用一群具有特定權值的粒子近似狀態估計值的方法。與KF方法不同，PF算法不受限于高斯假設，特別適用于非線性非高斯應用場景，已經在壽命預測領域得到了許多應用[10-11]。但是，PF算法存在粒子退化的缺陷，在經歷了一定的迭代步數后，許多粒子的權值變得極小。而粒子的退化會影響剩余壽命預測的準確度[12]，因此，如何有效降低PF方法中的粒子退化程度，進而減小預測誤差，是基于PF的壽命預測方法中存在的一大問題。選擇合適的重要性采樣概率分布函數是解決這一問題的有效方法。無跡粒子濾波(Unscented Particle filter, UPF)就是一種利用這種方式解決粒子退化問題的改進粒子濾波算法[13]。UPF結合了PF和無跡卡爾曼濾波(Unscented Kalman filter, UKF)的優點，利用UKF算法獲得一個合適的重要性采樣概率分布，從而有效降低粒子退化程度。為了解決基于PF軸承剩余壽命預測中的粒子退化問題，本文提出一種基于UPF的軸承剩余壽命預測方法，即通過UPF結合數學模型與軸承的狀態監測信號估計軸承的當前健康狀態，并給出其剩余壽命的估計值。

1 UPF算法

1.1 貝葉斯估計

大部分的動態系統都可以由兩個方程描述，狀態轉移方程和觀測方程為

θt=ft(θt-1,nt-1)

(1)

yt=ht(θt,vt)

(2)

式中：ft—Rnθ×Rnn→Rnθ為上一時刻到當前時刻的狀態轉移函數；ht—Rnθ×Rnv→Rny為當前狀態θt的觀測函數；nt為獨立同分布過程噪聲；vt為獨立同分布測量噪聲。

分別使用θ0：t={θ0,…,θt}和y1:t={y1,…,yt}代替當前所有狀態和所有觀測值。我們的目的是得到后驗概率p(θ1:t|y1:t)。根據馬爾科夫過程特性，我們無需追蹤所有已有狀態，只需遞歸地計算p(θt|y1：t)便可得到后驗概率。具體地，每一時刻的先驗概率密度分布函數和后驗概率密度分布函數分別如式(3)和式(4)所示

(3)

(4)

1.2 UPF算法

PF算法的本質是利用一群具有特定權值的粒子來近似系統狀態，通過更新粒子權值和粒子來實現最優估計。具體地，系統狀態后驗概率密度分布函數可以表示為

(5)

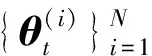
標準PF算法中，通常采用系統的先驗分布作為重要性采樣分布，這種做法能夠簡化計算過程，但是容易使PF算法陷入粒子退化問題中。與標準PF算法不同，UPF利用UKF生成重要性采樣分布，充分利用最新的觀測值，能夠有效地解決粒子退化問題。

UPF的具體實現步驟如下：

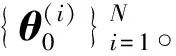
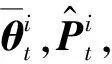
步驟3根據式(6)利用當前時刻t的測量值更新各粒子所對應的權值。

(6)

并根據式(7)對權值進行歸一化處理。

(7)

步驟4重采樣。為了增加有效粒子的數量，提高計算效率，需要移除權值極小的粒子，并復制權值較大的粒子，這個過程稱之為重采樣。一個簡單的實現過程如下[14]：

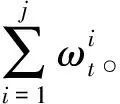
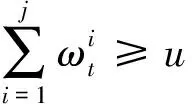
(8)

步驟5狀態估計。利用更新后的粒子及其權值估計當前時刻t的狀態

(9)

步驟6然后返回至步驟2，重復之后的步驟，直到t=T(T為測量值的數量)。

2 基于UPF的軸承剩余壽命預測方法

軸承的整個工作周期可以分為三個階段，正常階段，退化階段以及失效階段。當軸承處于失效階段時，意味著軸承已經不能正常工作，需要進行更換。因此，本文只考慮前兩個階段的剩余壽命預測。軸承的狀態監測數據有振動信號、溫度和聲發射等。其中，由于振動信號采集方便，而且對軸承的性能退化十分敏感，因而被廣泛應用于軸承的故障診斷和剩余壽命預測中[15]。因此，本文從振動信號中提取特征，將其作為軸承性能退化的指標。

本文提出的方法如圖1所示。根據已知的歷史失效軸承數據利用隨機過程模型建立軸承的退化模型。在針對具體軸承進行壽命預測時，首先判斷其是否開始退化，當檢測到其開始退化時，利用UPF方法結合數學模型和測量數據，更新模型參數，估計軸承的退化狀態，并實現軸承的剩余壽命預測。通常，信號的不同特征描述的是信號的不同方面，因而能從不同角度反映軸承的退化狀態。在軸承的故障診斷與壽命預測中，峭度對于早期故障比較敏感，但對于故障的發展惡化并不敏感，而均方根值(Root Mean Square, RMS)反映的是振動能量隨故障發展的增長，因而對于軸承故障發展程度較為敏感。因此，本文利用峭度監測故障的出現，采用RMS評估軸承的故障發展程度，并預測其剩余壽命。

圖1 基于UPF的軸承壽命預測方法流程圖Fig.1 Flowchart of the proposed method

2.1 軸承退化檢測

在軸承的整個工作周期中，軸承有很長一段時間都處于正常工作狀態。在這個階段，我們沒有必要預測軸承的剩余壽命。因此，檢測軸承的退化起點，僅在軸承的性能退化階段預測其剩余壽命能夠有效節約計算資源。此外，正確區分正常狀態與退化狀態的監測數據，能夠有效避免正常狀態數據的干擾，提高壽命預測的準確度。因此，本文在針對具體軸承進行壽命預測時，先判斷其工作狀態，當檢測到其開始退化時，才開始預測其剩余壽命。

軸承振動信號的峭度是一個無量綱參數，與軸承的負載及參數無關。通常，峭度指數對于軸承的早期故障比較敏感，但對于故障的發展與狀態惡化并不敏感。因此，本文采用振動信號的峭度值來判斷故障的出現，即確定軸承剩余壽命預測的起始點。首先，計算軸承正常工作狀態下振動信號峭度值的均值μ與標準差σm，定義軸承狀態正常的峭度值區間為[μ-3σm,μ+3σm]。狀態監測過程中，當tf時刻的峭度值mf超出該區間時，則認為軸承振動信號出現異常。由于振動信號的采集以及特征提取中存在一定的隨機誤差，會造成誤判。為了消除這一影響，引入Li等研究中的觸發機制來判定軸承的退化起始點，具體步驟如下：

步驟1首先，定義l= 0，當峭度值第一次超出3σm時，定義該時刻點為FPT0；

步驟2令l=l+1，當時間點tf滿足連續l+1個時間點的峭度值{mf+k}k=0:l滿足{|mf+k-μ|>3σm}k=0:l，則定義時刻tf為FPTl；

步驟3使l由1逐漸增大直到l滿足FPTl=FPTl-1，則認為軸承此時出現故障，并定義FPTl為軸承的剩余壽命預測起始點。

通常，由隨機噪聲造成的異常狀態不可能連續出現l+1次，因此上述觸發機制能夠很好地消除隨機噪聲對軸承退化檢測的影響。采用以上方法檢測到軸承退化后，在后續的狀態監測過程中，根據軸承振動信號預測軸承的剩余壽命，從而為軸承的維護維修提供參考。

2.2 退化模型

軸承的退化模型是用來描述軸承健康狀態與其工作時間關系的數學模型。由于RMS描述的是信號強度，能夠反應軸承整體損傷，對于軸承的故障發展程度較為敏感。因此，當使用2.1節中方法檢測到軸承退化后，采用RMS來表征軸承的故障發展程度。RMS是一個有量綱參數，會受到負載、安裝等工況的影響，因而容易引發錯誤的預測結果。為了降低這一影響，利用相對RMS值(Relative Root Mean Square，RRMS)作為健康指標，用于軸承剩余壽命預測。RRMS的具體定義為

(10)

式中：XRRMS(t)為信號采集時刻t的RRMS值；XRMS(t)為該時刻的RMS絕對數值；XRMS(FPTl)為軸承剩余壽命預測起始點的RMS絕對數值。

通常，機械設備的退化過程是一個隨機過程。機械設備隨機退化過程的不確定性主要來源于四個方面：①臨時不確定度；②單元-單元不確定度；③非線性不確定度；④測量不確定度。Si的研究中提出了一種包含前三種不確定度的自適應退化模型。結合該模型與軸承的退化特點，建立軸承的退化模型為

X(t)=a+λtb+σB(t)

(11)

式中：X(t)為時刻t的RRMS值；a為系統的初始狀態，通常等于0；λ為時變參數，代表系統的退化速度；b為系統的非線性度；σB(t)為服從正太分布N(0，σ2)的布朗運動。

在軸承的狀態監測過程中，很難準確地對軸承的運行狀態進行測量，因而采用振動信號這種間接測量方式反應其健康狀態，但間接測量結果與其真實狀態間存在一定的誤差。同時，信號處理與特征提取過程中都會產生一定的誤差。因此，得到的特征與軸承的真實狀態之間存在誤差，這些誤差統一作為測量噪聲。因而建立軸承的測量方程為

Y(t)=X(t)+ν

(12)

式中：ν為軸承的測量噪聲，服從正太分布N(0,γ2)。

由于工作環境和材料參數等各方面的原因，每個軸承的參數λ，b取值均不相同。為了準確地預測軸承剩余壽命，必須準確地估計各個參數的值。根據軸承的退化模型，可以得到其狀態轉移方程和測量方程

(13)

式中：η=σ(B(tt)-B(tt-1))服從正太分布N(0,σ2Δt)，Δt=tt-tt-1。

2.3 剩余壽命預測

軸承退化模型確定后，便可以通過1.2節所述的UPF算法步驟利用測量值對模型參數進行更新，得到測量時刻t的模型參數，并估計此時的退化狀態。利用退化模型傳遞現有分布，可以預測t+p時刻的狀態。在PF算法中，一種比較簡單的預測方法就是計算每個粒子在t+p時刻的狀態，從而得到系統的狀態。

(14)

假設t時刻得到的粒子能夠準確地表示t時刻的系統狀態，則可以通過遞推的方式，最終得到t+p時刻的狀態。遞推公式為

(15)

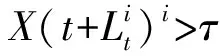
3 案例分析

為了闡述提出方法的有效性，采用實際試驗中得到的全壽命周期振動信號對提出方法進行驗證。并將提出方法與傳統PF方法進行對比，說明提出方法的優越性。

3.1 試驗臺與試驗數據

本文所采用的數據由FEMTO-ST機構提供，該數據曾用于2012年壽命預測與健康管理數據挑戰[16]。采集該數據的試驗平臺如圖2所示。通過加速性能退化技術，該試驗系統能夠在較短時間內收集軸承的全壽命周期數據。試驗中，軸承振動信號的采樣頻率為25.6 kHz，數據長度為2 560，每隔10 s采集一次。試驗中，分別采集了橫向和垂向的振動信號。但試驗過程中施加的力為徑向力，因此，橫向振動信號更能反映軸承的工作狀態。因此，本文選用橫向振動信號進行分析，從橫向振動信號中提取特征表征軸承的健康狀況。

圖2 加速壽命試驗臺Fig.2 Overview of the experimental platform

圖3為一個典型的軸承全壽命周期振動信號。由圖可以看出，軸承經歷了一段較長的正常工作時間，然后開始退化，一旦開始退化后，軸承的性能迅速退化直至失效。

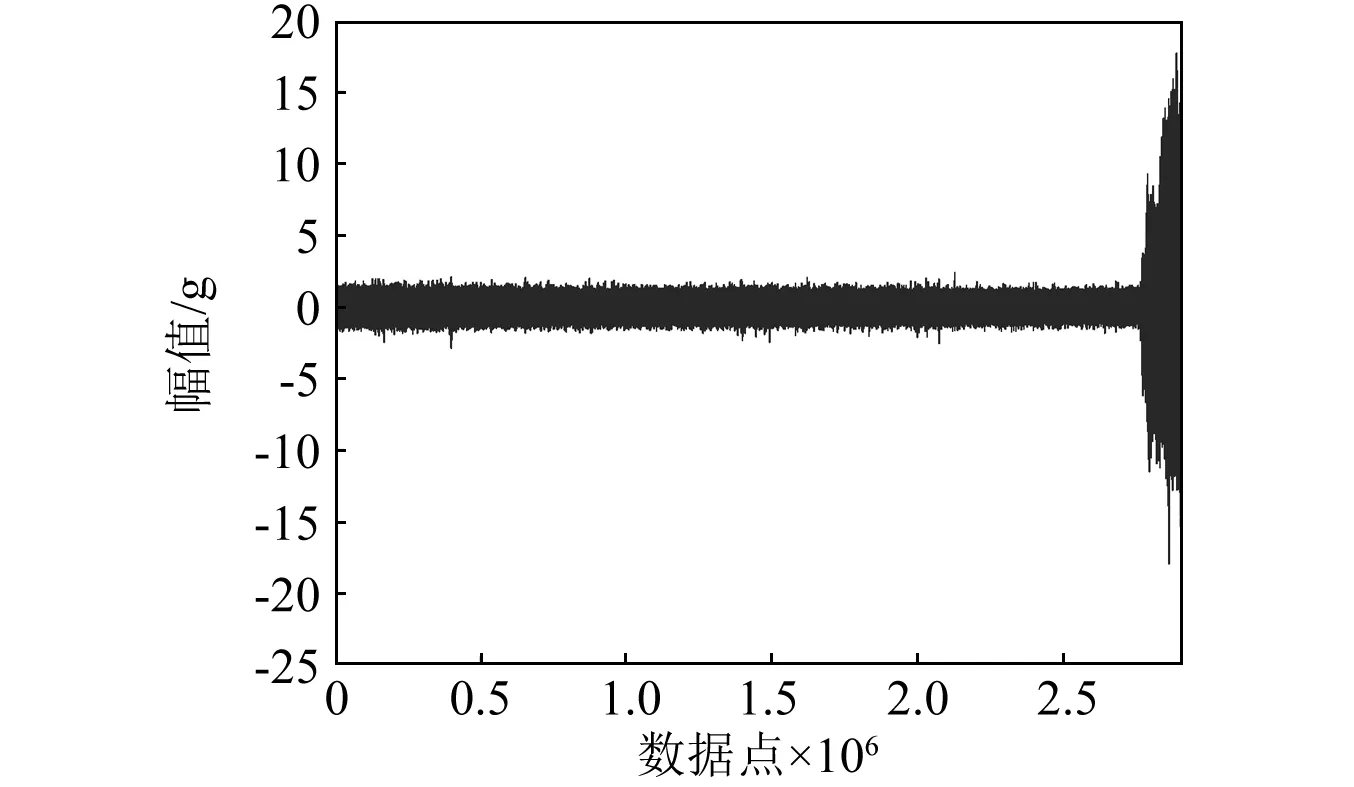
圖3 軸承振動信號Fig.3 The vibration signal of a bearing

3.2 軸承剩余壽命預測

本文提出的方法需要先判斷其是否進入退化階段，即找出第一個剩余壽命預測點，然后再對軸承進行剩余壽命預測。根據第2部分所述方法，提取軸承振動信號的峭度值與RMS，如圖4與圖5所示。首先，根據2.1節所述方法，利用峭度值判斷軸承退化起始點。由圖4可知，當軸承正常工作時，峭度值比較穩定，同時由于隨機噪聲的存在，這個過程中也會出現異常值。采用2.1節中所述觸發機制消除隨機噪聲的影響，結果表明，當t=10 910 s時，軸承開始退化，如圖4中的豎線所示。因此，選擇t=10 910 s為軸承的第一個剩余壽命預測點。相應地，圖5中的豎線表示軸承的退化起始點，此時軸承的RMS值變化較大，此后RMS值一直隨著退化程度的加深而增大。

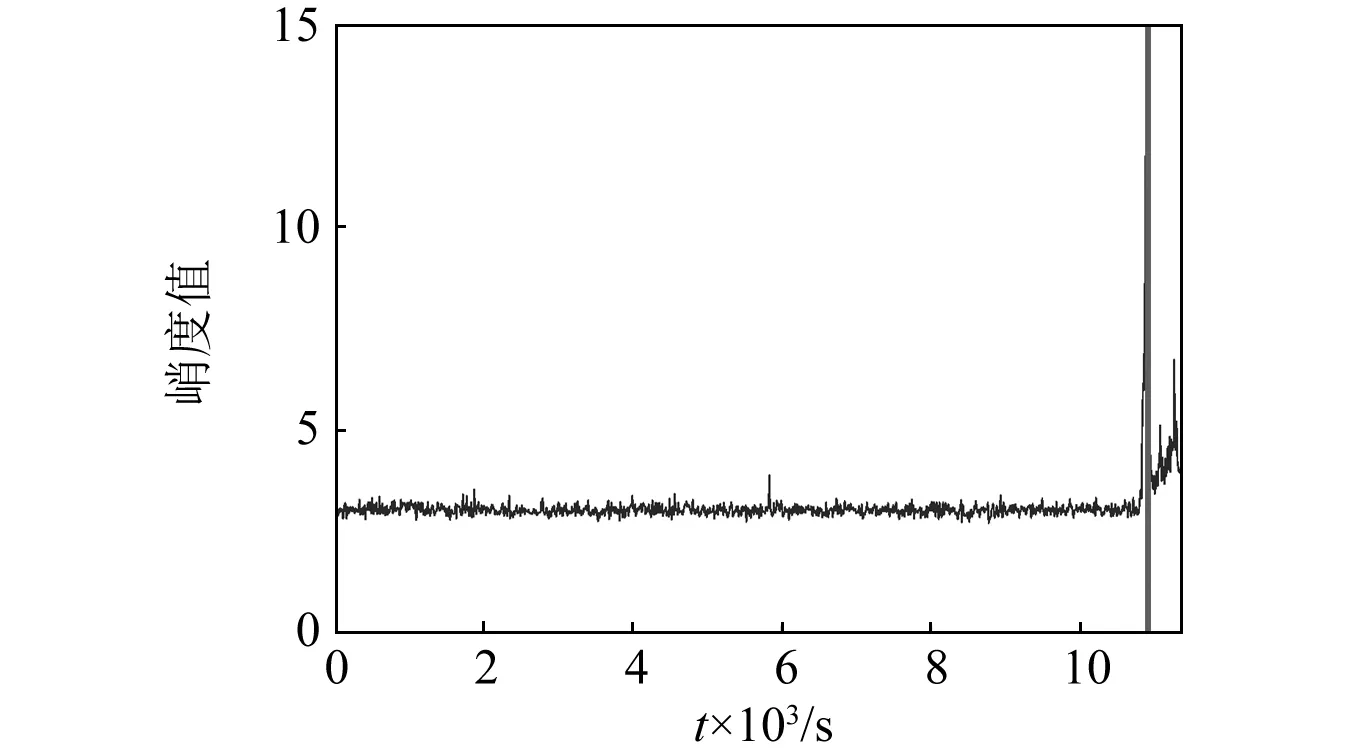
圖4 軸承振動信號的峭度值Fig.4 Kurtosis results

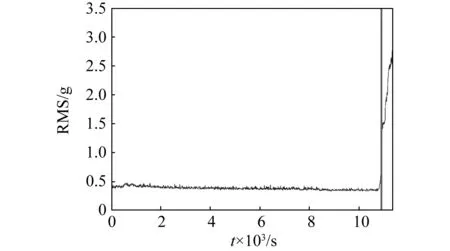
圖5 軸承振動信號的RMS值Fig.5 RMS results

檢測到軸承開始退化后，計算每一個信號采集時刻的RRMS值，利用2.2節與2.3節所述方法完成軸承的剩余壽命預測。圖6為退化模型參數的更新過程，圖中橫坐標0 s表示第一個剩余壽命預測點，后續橫坐標值均表示當前時刻距離第一個剩余壽命預測點的時間，圖7、圖8、圖9以及圖10中橫坐標的意義均與圖6一樣。由圖可知，剛開始進行參數估計的時候，由于涉及的測量信息較少，參數估計結果存在較大誤差。隨著測量數據的增多，參數λ與參數b均逐漸收斂于真實值。因此，采用本文提出方法能夠有效地利用測量數據估計退化模型參數。

為了說明本文提出方法的有效性，將PF方法作為對比。分別利用兩種方法對軸承退化階段的狀態進行追蹤，得到的結果如圖7所示。由圖可知，PF方法和UPF方法都能夠準確地追蹤RRMS值，在少數點處，UPF的估計結果比PF的估計結果更為準確。

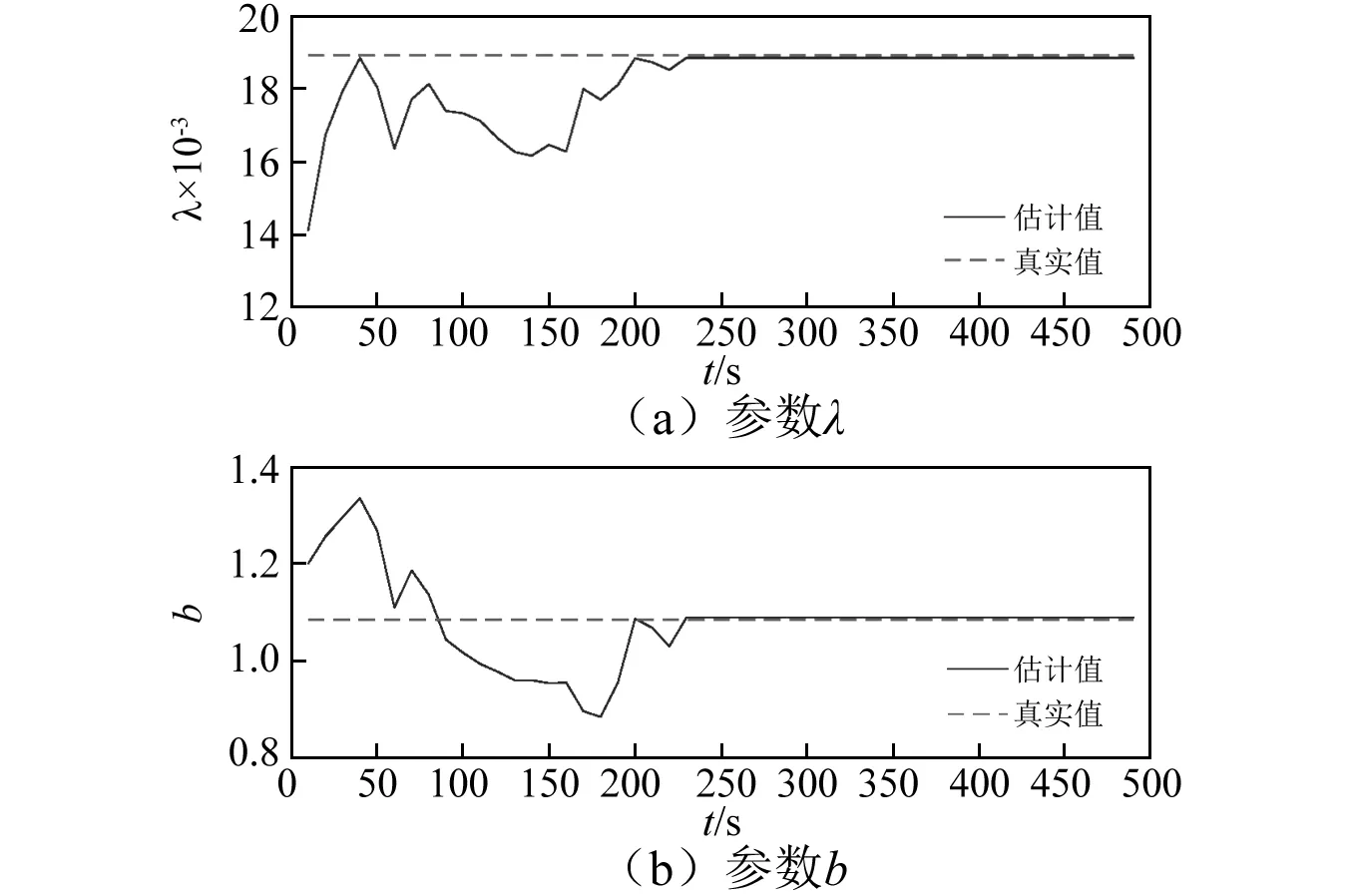
圖6 退化模型參數更新過程Fig.6 Update process of model parameters

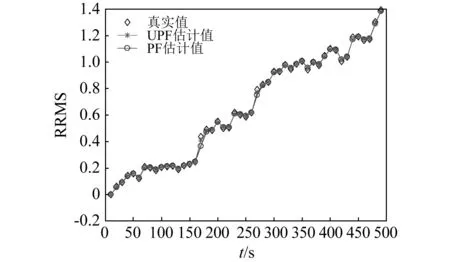
圖7 軸承退化過程中RRMS估計值Fig.7 RRMS estimations of bearing degradation process

為了驗證相對于PF方法，UPF方法能夠有效解決粒子退化問題，采用有效粒子數來衡量狀態更新過程中粒子的退化程度[17]。狀態估計過程中，兩種方法所選擇的粒子數均為1 000，整個過程中，兩種方法的有效粒子數如圖8所示。由圖可以看出，迭代開始后，兩種方法的粒子均迅速退化，但整個過程中，UPF方法的有效粒子數始終大于PF方法的有效粒子數。

為了驗證UPF方法在壽命預測中的作用，選用第10個時間點和第35個時間點的預測結果來說明UPF方法相對于PF方法的優越性。圖9為已知10組數據時的預測結果，由圖可以看出與PF方法相比，UPF的預測誤差較小。已知10組數據時，使用PF方法預測到RRMS值超過失效閾值的時間為580 s，而真實的失效時間為490 s，因此，其剩余壽命預測誤差為90 s。而當使用UPF方法時，預測到RRMS值超過失效閾值的時間為520 s，其預測誤差為30 s。圖10為已知35組數據時的預測結果，由圖10可知，隨著測量值的增加，兩種預測方法的準確度都隨之增加。但UPF方法的預測結果依然比PF方法好，此時，PF預測方法預測軸承的失效時間為520 s，預測誤差為30 s，而UPF方法預測軸承失效時間為480 s，預測誤差為10 s。UPF方法的預測誤差低于PF方法的原因可以解釋如下：在UPF方法中，每個粒子均采用UKF方法進行了更新，因而不會與實際狀態產生很大的偏差。在后續權值更新過程中，由于其與測量值相差不會過大，因而避免了大部分粒子權值過小發生退化，能夠更好地估計系統狀態。因此，UPF方法能夠有效解決PF方法中的粒子退化問題，提高軸承剩余壽命預測的準確度。

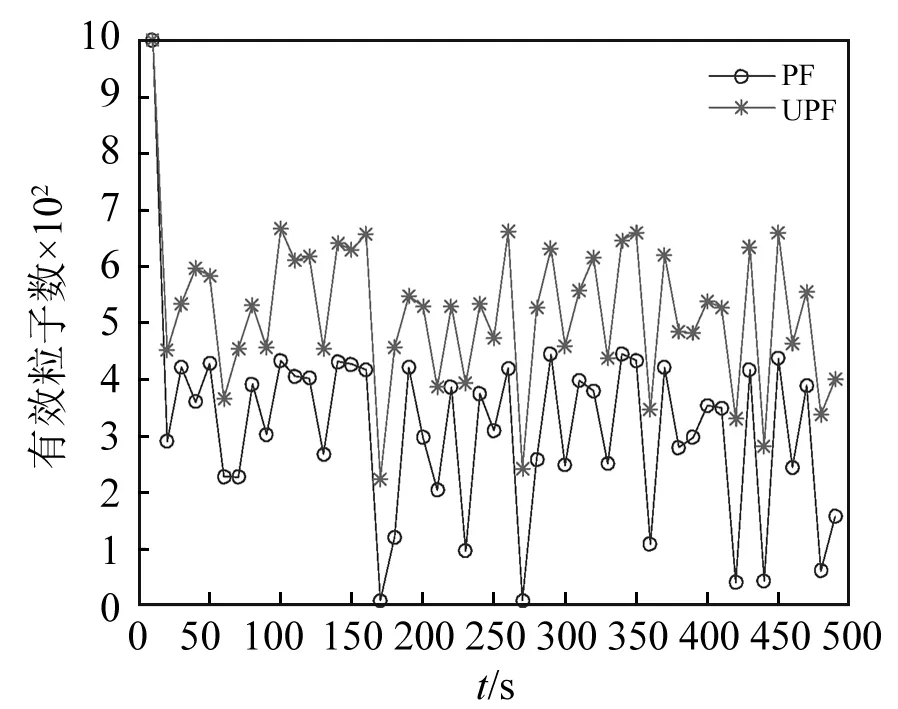
圖8 有效粒子數對比Fig.8 Comparison of the effective sample sizes

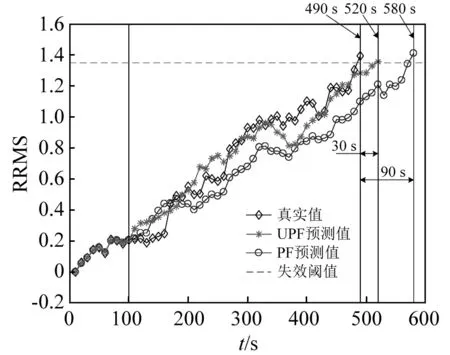
圖9 10組數據時的預測結果Fig.9 Prediction results with 10 measurements

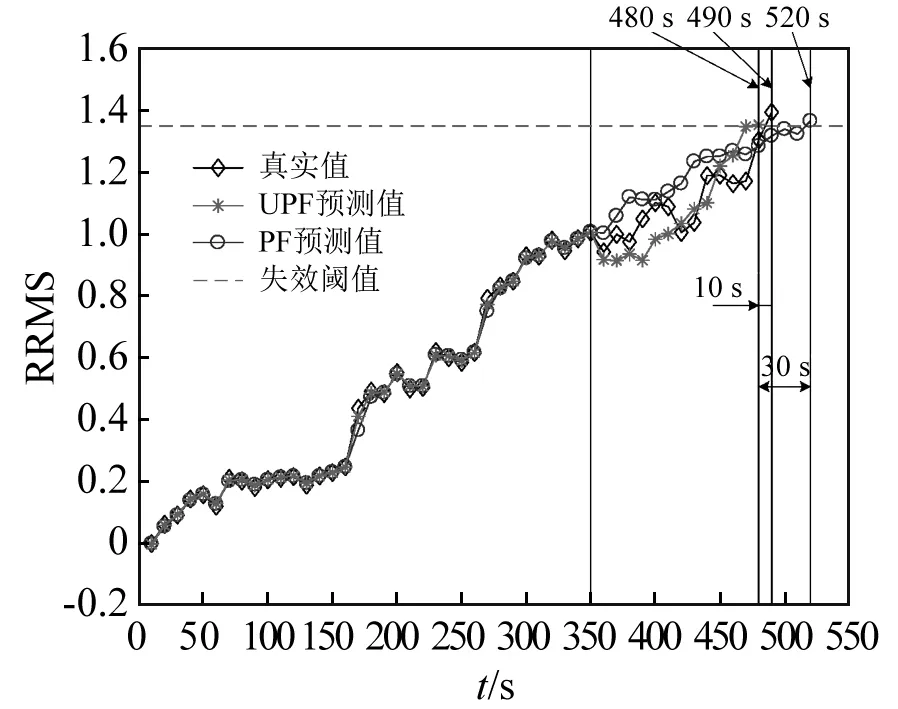
圖10 35組數據時的預測結果Fig.10 Prediction results with 35 measurements

4 結 論

PF算法是一種廣泛用于解決目標追蹤問題的方法。近年來，PF技術被引入剩余壽命預測領域。但隨著迭代次數的增加，PF算法會出現粒子退化問題。UPF算法結合PF和UKF，能夠有效解決這一問題。本文提出了一種基于UPF的軸承剩余壽命預測方法，結合隨機過程模型與UPF方法，對退化過程中的軸承狀態進行追蹤，并完成其剩余壽命預測。結果表明，UPF方法能夠有效彌補PF方法粒子退化這一缺陷，與傳統PF方法相比，本文提出方法能夠更加準確地預測軸承的剩余壽命。