數形結合在解題中的應用
吳新平(湖北省監利縣蘆陵中學,湖北 監利)
在歐洲,早在17世紀,法國著名數學家笛卡爾就已經針對數形結合進行了系統的總結與分析。尤其是笛卡爾通過坐標系的建立從而創立了解析幾何學,更是為數學的研究提供了更加廣闊的思路。中學作為學生九年義務教育以及進入大學教育的一個過渡階段,采用系統的教學方式培養學生發現問題和解決問題的解題思路,能夠對學生之后的學習過程進行有效的培養。
一、借助于方程的曲線解決最值問題
方程曲線是在進行方程解答過程中極為常見的一種方式方法,在具體的運算過程中,應該注重對這一方式的推廣和運用。以下題為例:
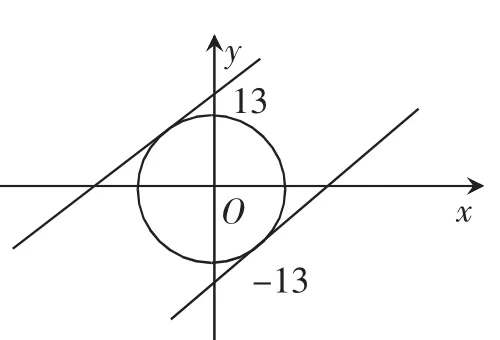
圖1
通過對題目進行分析不難了解到,針對二元函數y-3x=b在限定條件下求值問題,如果采用構造直線的方式來進行,將能夠對解題方法進行簡化。具體解析:首先應該令y-3x=b,從而得出 y=3x+b,即可將原來的問題轉化為:在橢圓形上求一點,使得過該點直線的斜率為3,同時可以顯示在y軸上的截距最大或者最小。通過畫圖可以了解到(圖1),當直線與橢圓形相切時,則有最大截距與最小截距。
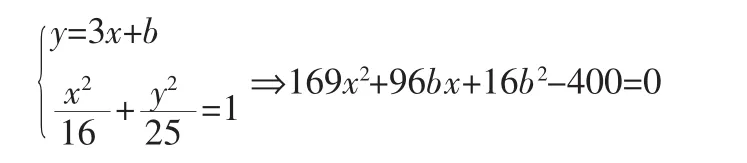
由Δ=0得b=±13,故y-3x的最大值為13,最小值為-13。
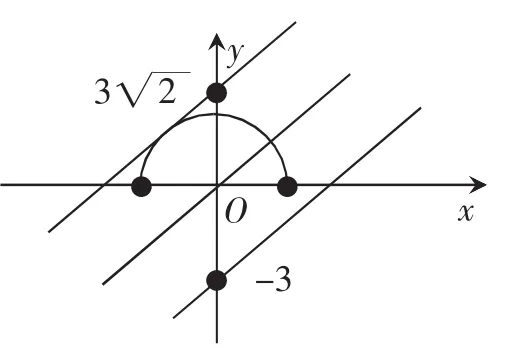
圖2
二、借助于函數圖象解決取值范圍問題
采用函數圖象的方式進行數學取值范圍問題的解決也是較為常見的方法之一,在具體進行問題解決的過程中,可以以下題為例:
三、借助于函數圖象解決不等式的值域問題
采用函數圖象來表示不等式之間的關系同樣也是在數學教學以及階梯過程中常見的一種方法,以下題為例:
這一題不采用數形結合的方法,采用常規的解法如下:
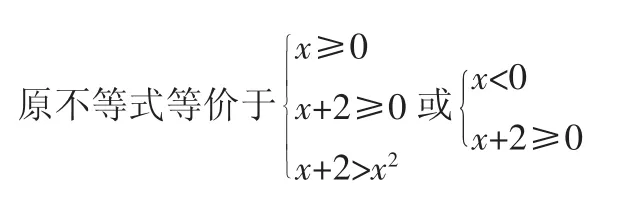
通過這一解法需要對x的各個幾何進行劃分,極易出錯:解得0≤x<2或-2≤x<0,故原不等式的解集為或
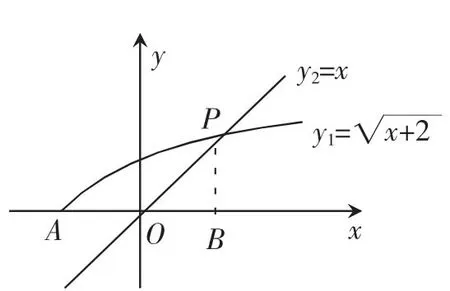
圖3
同時可以了解到,在解決具體問題的過程中,采用數形結合的方式將代數問題進行了圖像具化,只需要設置兩個函數,同時結合圖像就能夠將答案進行總結,方便快捷,同時也能使思路變得更加清晰。
總之,數形結合的實質是將數學常規語言以及較為常見和直觀的圖像圖形進行聯系,廣大數學教師隊伍應該對數形結合思維更加重視,使學生的課程學習過程更有效率。

