回歸教材 發展思維能力

潘強 李鋒

《普通高中數學課程標準（實驗）》（以下簡稱“課標”）提出：“高中數學課程應注重提高學生的數學思維能力，人們在學習數學和應用數學解決問題時，不斷地經歷直觀感知、觀察發現、歸納類比、空間想象、抽象概括、符號表示、運算求解、數據處理、演繹證明、反思與建構等思維過程，這些過程是數學思維能力的具體體現……”，那么，怎樣才能有效提高學生的數學思維能力？眾所周知，教材是一種豐富的課程資源，是課堂教學中師生互動的橋梁，同時也是學生開展思維活動、發展思維能力的主要載體，下面，筆者選取人教A版《數學選修2-1》（以下簡稱“教材”）中的具體例子，談談如何回歸教材，落實“用教材教”，充分發展學生的思維能力.

1 重視章引言及課后拓展性材料的教學，創設情境激活學生思維

章引言是教材的一部分，是教材編寫者精心設計，它置身于每一章的開頭，以簡明扼要的語言介紹本章的內容、地位及應用，以及蘊涵其中的思想方法與人文背景，體現本章知識的生長點與思維方法，是學生學習本章的開場白，作用不容忽視，一些拓展性材料如“觀察與猜想”、“閱讀與思考”、“探究與發現”、“信息技術應用”等由于不在教材正文常常被忽視，筆者認為它們作為新教材特色之一是教材正文有益的補充與延伸，具有較強的靈活性與開發空間.

案例1 平面截圓錐

教材在章引言中介紹了圓錐曲線的來源——“平面截圓錐”，在“2.2.1橢圓及其標準方程”課后的“探究與發現”欄目以“為什么截口曲線是橢圓”為題，介紹了數學家Germinal Dandelin從純幾何角度出發給出的證明，由此可見，教材對“平面截圓錐”的教學功能非常重視，以其為“源”引出概念，以其深刻背景為“墊”，統一了概念和名稱，以其簡捷漂亮的證明為“流”，疏通了概念，學生從中感受到圓錐曲線來源于現實生活，體會數學與生活的聯系，欣賞圓錐曲線的一種和諧統一的美，經歷了由具體實例觀察發現、抽象概括出圓錐曲線以及猜想證明的思維歷程，

教學中要有效利用這些素材創設有效情境激發學生思考與探索，要“挖”出隱藏于教材之中內涵豐富的思想，要利用每一個契機發展學生思維，明確橢圓生成方式之一——平面截圓錐，教材在數學家Germinal Dandelin的幾何證明之后又提出一個問題：用一個與圓柱的母線斜交的平面截圓柱，你能仿照上述方法，證明所得到的截口曲線也是橢圓嗎？

例1（2008年高考浙江卷·理10）如圖1，AB是平面a的斜線段，A為斜足，若點P在平面a內運動，使得△BP面積為定值，則動點P的軌跡為 （? ）

A.圓

B.橢圓

C.一條直線

D.兩條平行直線

顯然，命題者正是以平面截圓柱為背景來考查學生的思維能力，體現了高考“源于教材而高于教材”的命題思想，因此，平常教學中一定要回歸教材，研究教材，滲透思想，發展思維.

2 變式引領，開放探究，充分發揮教材例題與習題的教學功能

例題與習題都是經過教材編寫者精挑細選的，它們可改造成為探究性問題的素材，對其進行“變式練習”是開發學生思維的有效方法，

案例2（教材P49習題2.2A組7）如圖2，圓0的半徑為定長r.A是圓0內一個定點，P是圓上任意一點，線段AP的垂直平分線，和半徑OP相交于點Q，當點P在圓上運動時，點Q的軌跡是什么，為什么？

利用定義學生容易得出點Q的軌跡是橢圓，倘若就此擱筆，無異于“入寶山而空返”，錯失一個發展學生思維能力的好機會，筆者曾對該題進行了適度開發，充分挖掘蘊涵其中的教學功能，現簡要摘錄片段如下：

教師：若條件沒有點A在圓O內的限制，點Q的軌跡是什么？

通過演示，學生發現：當點A在圓上，點Q與0重合;當點A在圓外，點Q“不翼而飛”，表明直線l與半徑OP沒有交點，如何改變題設的條件使得交點Q出現，其軌跡又是什么？（借助畫板直觀演示，最后學生共同歸納出以下情形，如圖3）

生：當點A在圓外時，直線l與OP所在的直徑的交點的軌跡是以0，A為焦點的雙曲線左支位于圓O內的部分;直線l與射線PO的交點的軌跡是以0，A為焦點的雙曲線的左支;直線l與直線OP的交點的軌跡是以0，A為焦點的雙曲線，

本例通過開放探究，開拓學生思維，用運動變化的觀點揭示曲線的變化規律，訓練學生觀察、歸納、運動變化、數形結合、分類討論的思想方法，欣賞并體會其中蘊涵的數學美，提升思維品質，

教師：若直線AM，BM斜率之積為4/9，點M的軌跡方程如何？由此你發現了什么？

通過對例題的適當改編，進一步激活學生思維，并創設情境讓學生“拾級而上”，知識的生成自然、水到渠成，學生經歷從特殊到一般的歸納思維，接受函數與方程、歸納類比、分類討論、化歸轉化等數學思想方法的熏陶，體驗了先猜想后證明的數學理性思維的本質，

上述案例2通過改變題設的條件引發學生進行開放探究，案例3通過對不同形式的特殊實例的研究中發現規律，并將其推廣到一般的情形，以此擴大題目的訓練功能，與其煞費苦心從大量泛亂的教輔材料中挑選，不如從貼近學生實際的教材中精選例題或習題，通過改變題目的設問方式、加強或削弱條件、在一定范圍下將該題進行引申或推廣等進行有意義的變式訓練，實踐證明，“變式練習”重復而不呆板，為學生思維能力的發展搭好了“腳手架”，既夯實了雙基，又提升了思維的品質.

3 充分挖掘教材例、習題中蘊含的數學思想方法，發展數學思維能力

張奠宙教授提出：數學教師要具有數學思想方法的教學意識，掌握數學思想方法的內涵，將數學思想方法用于解題，發展學生的數學思維能力，因此，我們要以形成數學思想來統領日常的課堂教學，尤其是函數與方程、數形結合、分類討論、化歸轉化思想，比如上述案例無一不滲透這四種重要的思想方法，在教師精心設計與合理引導下，通過變式引領，開放探究，發展學生的直觀感知、觀察發現、歸納類比、抽象概括、推理證明等思維能力，“課標”把推理論證能力確定為一項基本能力，對推理論證能力的要求既包括原來的演繹推理，又包括歸納、類比猜想等合情推理，推理論證被認為是數學學科以及數學家實踐的中心，是進行數學學習活動必備的首要的能力，因此教學中，要引導學生正確處理猜想與證明的關系，即不僅注重數學發現、創造過程中的合情推理——歸納與類比，而且將這種非形式化的探索式論證轉化成有效的數學證明，比如截口曲線是橢圓的幾何證明;案例3的代數證明等，這樣，學生的思維不只是停留在感觀的基礎上，而是向深層次發展——繼續探究問題的本質，用理性思維去驗證所得的猜想.

4 充分利用教材進行審美意識的培養，體會數學的美學意義

圓錐曲線這部分內容，處處都有“美”的痕跡，值得大力開發，對學生進行審美意識的培養，提高審美能力，比如“平面截圓錐”體現圓錐曲線光滑美、動態美、統一與和諧美;圓錐曲線的定義具有統一美與數學語言美;圓錐曲線的方程蘊涵簡潔美等等，本文幾個案例的探究過程中，也處處體現出上述各種美，還有解題方法的簡潔美以及所折射出數學思維的理性之美等，所有這些在教師精心設置的問題情境下，通過學生的親身體驗、用心感悟，培養其強烈的審美意識，同時對數學的美深刻的感悟，對數學的美學意義深切的體會，進一步提高學生學習的興趣和探究數學問題本質的欲望，

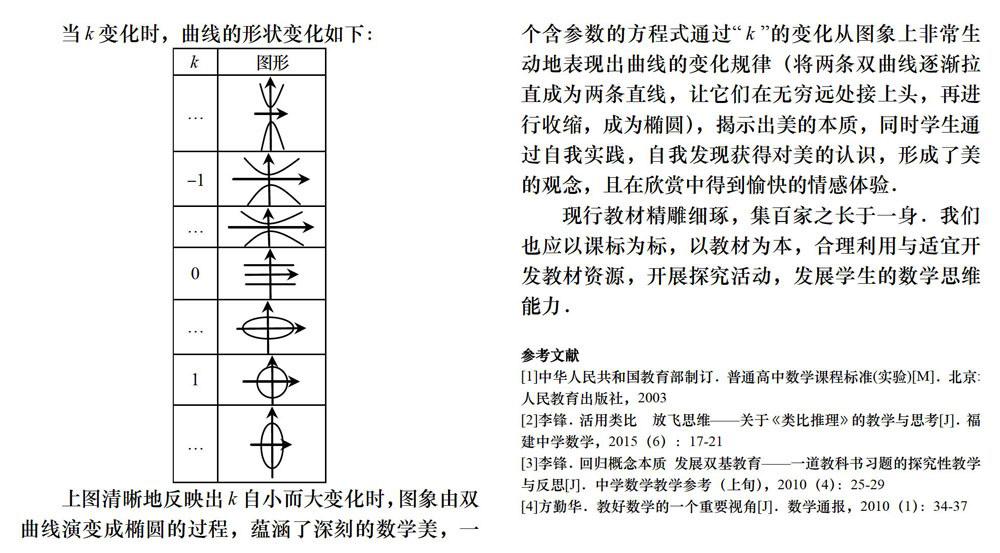
案例4（教材改編）幾何畫板探索方程KX2+y2=1所表示的曲線當K變化時，曲線的形狀變化如下：

上圖清晰地反映出K自小而大變化時，圖象由雙曲線演變成橢圓的過程，蘊涵了深刻的數學美，一個含參數的方程式通過“K”的變化從圖象上非常生動地表現出曲線的變化規律（將兩條雙曲線逐漸拉直成為兩條直線，讓它們在無窮遠處接上頭，再進行收縮，成為橢圓），揭示出美的本質，同時學生通過自我實踐，自我發現獲得對美的認識，形成了美的觀念，且在欣賞中得到愉快的情感體驗，

現行教材精雕細琢，集百家之長于一身，我們也應以課標為標，以教材為本，合理利用與適宜開發教材資源，開展探究活動，發展學生的數學思維能力，

參考文獻

[1]中華人民共和國教育部制訂.普通高中數學課程標準（實驗）[M].北京：人民教育出版社，2003

[2]李鋒，活用類比放飛思維——關于《類比推理》的教學與思考[J].福建中學數學，2015 （6）：17-21

[3]李鋒，回歸概念本質發展雙基教育——一道教科書習題的探究性教學與反思[J].中學數學教學參考（上旬），2010 （4）： 25-29

[4]方勤華.教好數學的一個重要視角[J].數學通報，2010 （1）： 34-37