基于MEA模型的作戰飛機裝備保障需求研究
陳 博,徐常凱,杜加剛
(勤務學院航材四站系,江蘇 徐州221000)
隨著部隊戰斗力的不斷提升與發展,航空兵部隊參加演習作戰任務越來越頻繁,后勤保障部隊的保障壓力也越來越大,不斷擔負各種各樣的作戰保障任務,在作戰任務中某一項備件不能夠正常使用都可能會導致飛機發生因缺件而停飛的現象,使航空兵部隊的作戰效能大大降低,對整場演習作戰任務產生不良影響。現在大多數研究集中與對平時的作戰裝備消耗預測上,由于在作戰條件下的影響因素復雜,不確定因素大,所以對于作戰裝備預測消耗研究相對較少,且采用的一般神經網絡、灰色系統等算法都具有一定的魯棒性,預測結果易陷入局部最優解,難以準確地把握裝備的消耗預測水平,本文結合保障經驗與相關文獻,對作戰裝備保障的消耗影響因素進行深入分析,并在此基礎上,對基于思維進化算法的作戰飛機可修件保障需求量確定的求解步驟進行詳細介紹。
1 裝備消耗數量預測影響因素分析
攜行裝備的消耗數量受不同種類的影響因素的制約,與此同時,這些不同種類的因子對消耗量的影響程度也各不相同,通過數據的統計與分析,可將影響攜行器材消耗數量的因素分為四大類[1],包括任務因素、裝備的可靠性因素、人為因素以及地理環境因素。
(1)任務因素
不同種類的任務模式對攜行裝備消耗數量的影響可謂千差萬別,例如在航空兵進行空中進攻作戰時,其裝備的消耗量較大,進行防御作戰時作戰裝備消耗數量相對較小,對于任務的影響程度可以采用飛機的出動強度、起落架次以及空中作戰時間等參數進行量化[2],其根據具體執行任務情況而定。
(2)攜行裝備的可靠性水平
攜行裝備的可靠性水平主要是指作戰裝備在一定時間內、在一定條件下無故障地執行指定功能的能力或可能性[2]。可通過可靠度、失效率、平均無故障間隔等來評價攜行裝備的可靠性,在此基礎上考慮保障任務的實際情況,包括執行任務飛機上的裝備的裝機時間以及歷史任務的消耗數據。裝備裝機時間主要是指在執行任務時飛機上的裝備的工作情況,對于裝機時間長的裝備其剩余壽命較短,所以在預測時其需求量很可能需要增加。據統計戰時裝備故障率λ(t)根據裝備類型的不同而服從三種不同的分布包括指數分布、正態分布以及威布爾分布[3],通過各分部服從的概率分布密度以及可靠度的計算,可以表示出各類部件的故障率,服從不同分布的故障率函數的計算方法如下所示:
1)指數分布
根據保障經驗故障率服從指數分布的裝備約占攜行裝備的90%,大部分電子設備就屬于這類分布,服從指數分布的裝備其消耗特點主要具有無記憶性即在t時刻后,其發生故障率與t時刻之前的狀態無關,其壽命長短不會縮短。為方便敘述,設攜行裝備第項器材(i=1,2,3,···n)服從指數分布,j為該項器材失效的次數,由此可計算出該項作戰器材的故障率[4]:
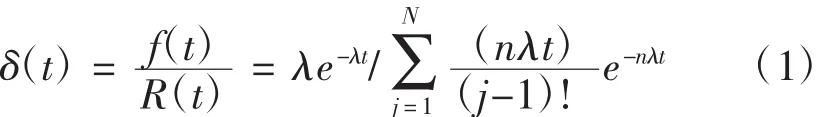
其中n表示單個裝備上該項器材的安裝的數量,1/λ表示第i項作戰裝備的平均故障間隔時間(MTBF),t為該項作戰裝備的實際使用時間,N表示在作戰任務中的總失效次數。
2)正態分布
攜行裝備保障中裝備壽命服從正態分布的分布函數器材發生第j次故障的概率為:

其中μ為器材壽命均值,可用于表示為第i項攜行裝備的平均故障間隔時間,σ為標準差,可由該項器材的長期保障數據經驗得到,-∞<t<+∞;其可靠度函數為:

可以計算出服從正態分布的作戰裝備的故障率為:

此類作戰裝備故障的產生原因是由于細微的器材消耗累積而成的,一般可用于計算非金屬的常進行磨損的器材。
3)威布爾分布
威布爾分布主要適用于對部分不可修復類的攜行器材的壽命分布函數進行擬合[5],當第i項作戰裝備服從參數為(α,β)時,其概率密度函數以及分布函數為[6]:

其中α為形狀參數;β為尺度參數;t≥0;其可靠度函數為:

可計算出服從威布爾分布的作戰裝備故障率函數為:

由上述可知通過輸入執行某次任務的作戰裝備器材的相關參數即可得到計算出概念器材的故障率,例如假設不可修復器材A是故障率服從指數分布的電子類器材,單機安裝數為2,其平均故障間隔時間為300 h,已經使用18 h,在某次作戰任務中飛機的空中戰斗時間為8 h,通過公式可計算出器材A發生第2次故障的故障率為:

(3)人員因素
在某些任務環境下,由于裝備保障條件較為惡劣,人為的因素對攜行裝備消耗的影響更大,裝備保障工作人員的保障水平就是其中一項非常重要的影響因素,裝備保障人員在進行裝備保障的過程中對器材的收發是否符合規范流程、對器材的管理是否按照業務規范、對器材的封裝保管是否細致正確,這都將影響攜行裝備的消耗量,特別是在特殊的任務環境下,對保障業務越熟悉制定的保障計劃以及處理應急的時間就越合理,攜行裝備需求量就越小。
(4)地理環境因素
地理環境主要是指裝備保障部隊在執行保障任務過程中所處地形、氣候、溫濕度等自然環境因素,其對攜行器材的消耗數量的影響也是十分巨大的,例如在高原地區因其空氣稀薄、溫度低、晝夜溫差變化劇烈、風沙灰塵較多、紫外線強烈等原因使液壓系統、裝備氣源、電氣、動力系統等航空設備的消耗量增加;與此同時,相關研究表明溫濕度的急劇變化或者過高、過低對通信設備會產生一定的不良影響。按照以上原則并根據相關文獻[7]進行的層次分析法,對不同屬性的攜行裝備和地形地貌進行分類,并依據其屬性對其受環境的影響程度進行量化,量化結果如表1.

表1 環境對攜行裝備消耗的影響因素量化
2 基于MEA算法的可修備件需求預測模型
在對作戰裝備消耗的各影響因素進行分析的基礎上,本文采用思維進化算法來進行優化,思維進化算法(MEA)是在傳統的種群算法的基礎上發展形成的啟發式搜索算法,其主要是在一定的約束范圍內通過不斷的迭代,找到對于目標函數的最優值。
思維進化算法采用了遺傳算法的相關概念包括“種群”、“個體”、“環境”等概念并在此基礎上進一步細分,設立全局公告板用來實現各種群之間信息的交流,設立局部公告板記錄子種群的進化過程,其具體過程包括:
(1)網絡初始化
由于思維進化算法沿用了遺傳算法的群體、進化等概念,因此網絡初始化部分基本相同,這里可以借鑒遺傳算法的網絡初始化部分內容。
(2)子群體生成
根據適應度函數計算個體適應度值,得分最高的前M個個體選定為優勝個體,(M+1)~(M+N)個個體作為臨時個體,以優勝個體和臨時個體為中心,分別生成M個優勝子群體和N個臨時子群體。
(3)趨同操作
各子群體內部個體進行局部競爭轉變為勝者的過程,競爭過程持續到子群體成熟,即不再產生新的勝者,此時的子群體得分為最優個體的得分,并將結果粘貼到全局公告板上,直到所有子群體成熟,趨同工作才結束。
(4)異化操作
成熟子群體之間為成為勝者而進行的全局競爭,從全局公告板上比較優勝子群體和臨時子群體得分,通過得分篩選出全局最優個體。異化結束后,計算最優個體適應度值,判斷是否滿足迭代次數和精度要求,不滿足則返回網絡重新進行(2)~(3)步操作。進化結束后解碼最優個體作為網絡結構初始權值和閾值,本文中模型的建立和運算在Matlab環境中進行。思維進化算法的優化過程如圖1所示[8]。
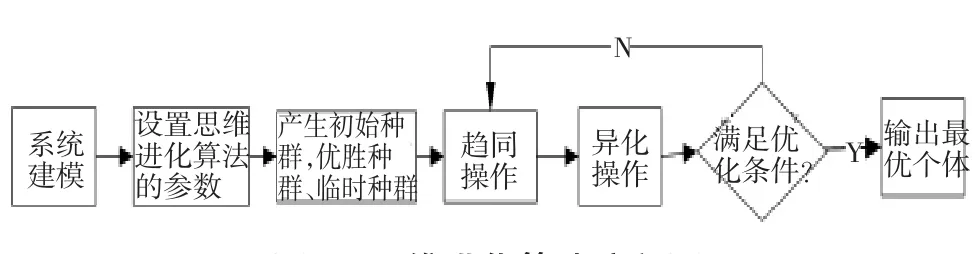
圖1 思維進化算法流程圖
算法初始先隨機選取n個群體,并根據設置的函數計算各群體對應的分數,再在此基礎上對數據進行趨同和異化的操作,本文將某次作戰飛機消耗器材分為為N個。按照正態分布隨機抽取Nj個種群,追求經濟的最小化,從而確定出Y個優勝子群體和P個臨時子群體,在此基礎上對各個子種群進行趨同操作進行種群遷徙,遷徙策略公式為:

其中Ωi(t)為t時刻種群的行為;δi(t)為其相應的變化量;In(t)為其包含信息的濃度;Fbi(t)表示在整個種群搜索的結果;hbi(t)表示某個種群在尋優過程中的結果;c1與c2表示學習因子;r1和r2表示之間的隨機數;?為慣性權重。由此可以進一步挑選出優勝種群,并在此基礎上進行變異操作,將成熟子群體作為中心點進行搜索,產生新的種群,并根據評級函數與之前的種群進行競爭,再按照約束條件判斷在此備件需求預測的情況下,是否能夠保證飛機可用度達到標準,最終輸出作戰飛機器材配置數據。
3 算例分析
本文在上述算法分析的基礎上,收集作戰飛機的裝備保障的相關數據,結合部隊的具體保障實際,對算法中的參數進行具體的假設,并在此基礎上進行計算檢驗,證明算法的有效性與合理性。
本文通過Matlab軟件實現對作戰裝備消耗數量預測的思維進化神經網絡組合模型[9],并對預測出的結果進行分析,選取空軍某一殲10飛機裝備保障部隊在執行過去10次轉場保障任務中的某項攜行器材的消耗數量,首先取前5組數據作為訓練數據對思維進化算法神經網絡進行訓練,剩余5組作為測試集對訓練出的模型閾值進行測試,網絡共進化學習100次,部分數據如表2所示。

表2 攜行裝備的各項影響因素預測消耗數據
先將數據進行思維進化優化,再將其帶入到神經網路中進行優化計算,根據算法輸入端與輸出端的個數,設置中間層的節點數,其參數具體設置如表3.

表3 參數設置表
最終完成網絡訓練,其優勝子種群的趨同過程如圖2所示。

圖2 優勝子種群優化
其臨時子種群的趨同優化過程如圖3所示。

圖3 臨時子種群優化
最終選出得分最高的種群,得到該次任務該項器材最優的消耗預測數量,與實際任務的平均誤差為1.168 3%,具體數值如表3所示。

表3 不同任務的器材消耗數量
4 結語
作戰飛機裝備保障需求預測是作戰備件供應保障的重要內容。本文首先對各作戰飛機裝備消耗的影響因素進行的深入分析,并在此基礎上,充分構建初始種群然后通過思維進化算法進行優化,最后通過具體算例進行實現,結果表明該方法能夠實現在一定條件下裝備需求預測功能且精度較高,有很好的實用價值,對于增加飛機備件保障的軍事效益與經濟效益具有重要意義。

