電能質量暫態擾動模糊分類分析

, , ,

(1.國網安徽省電力有限公司，合肥 230000;2.南瑞集團有限公司(國網電力科學研究院有限公司)，南京 210000)

0 引言

隨著電網規模的不斷發展，各類用電設備越來越多。一些性能高、效率高的敏感性高科技設備對電能質量的要求也在不斷提高，要求電網電能質量能滿足不同設備的使用需求[1-3]。而設備運行過程中容易產生電磁擾動信號等，對電能質量造成很大影響，對電能質量擾動信號的分類監測成為重點[4-6]。電能質量擾動分類主要從擾動信號特征提取和信號識別來實現[7]。目前應用較多的特征信號提取法包括小波變換[8-10]、傅里葉變換[11-13]、S變換[14]，對特信號的識別主要包括基于規則的分類[15]、基于支持向量機分類[16-18]和人工神經網絡分類法[19]等。本文在綜合相關研究方法的基礎上，采用小波變化來實現對平穩信號和非平穩信號的特征提取，并通過改進的支持向量基法來實現一對多的特征向量分類，從而滿足電網電能質量暫態擾動信號的識別和分類。

1 特征擾動信號提取

1.1 小波信號去噪

電能質量暫態擾動主要有電壓的暫升和暫降，電壓終端、暫態脈沖和暫態振蕩。該類型擾動信號通常采用暫態時間與電壓的變化關系來展現。這種暫態擾動在某一時間段內，不僅可以以單一形式發生，同時幾種擾動信號能夠相互組合，如電壓暫降和暫態振蕩等，變為復雜度更高的組合電能質量暫態擾動。因此，電網質量暫態擾動信號是一種多變的形式。

實際電網中，由于設備運行、外界環境電磁干擾等使得設備采集到的電能擾動信號包括多種復雜的噪聲信號，使得造成擾動信號完全掩蓋了噪聲信號，因此就需要去掉信號中的噪聲分布。根據小波去噪遠離，對于一個噪聲信號，可表示為式(1)。

S(t)=f(t)+ε*e(t)t=0,1,…n-1

(1)

上式中：S(t)為帶噪信號；f(t)為擾動信號；e(t)為噪聲信號；ε為信號偏差。對于e(t)可以認為是一個服從N(0,1)的高斯白噪聲。

獲得了電能質量信號后，若需要從信號中提取擾動信號，首先需要將噪聲信號從擾動信號分離。對于電網中電能質量擾動信號通常為一類低頻穩定信號，而噪聲信號更多的表現為高頻信號。在經過小波變換后，擾動信號的小波系數具有較大幅值，而噪聲信號則依然表現為高斯分布，具有的小波系數幅值較小。因此，可通過選定合適的閾值來分離噪聲信號和擾動信號，考慮到軟硬閾值在缺陷，本文采用一種改進的閾值函數來進行信號的分離，如式(2)。

(2)

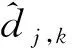
圖1 小波去噪信號流程

1.2 小波信號提取

在進行擾動信號分類前，需對信號進行處理選取能夠表征擾動信號的特征量來作為輸入量。特征量的選取直接關系到后續電能質量擾動信號的的分類效果，其中電能擾動信號的小波變換系數和分解層數的確定是實現小波信號提取的關鍵[20]。

1.2.1 小波基函數的確定

目前針對小波函數的選取主要根據工程經驗、應用對象以及小波基函數的性質來選取。針對電能質量擾動信號特征，要求選取的小波函數在時域和頻域上具備優異的局部性，且對電網中的不規則變化能較快反應。同時，在對于暫態電能質量，在進行時域分析時，要求小波變換能夠準確提取非穩態信號的突變成分，即在特定尺度上實現電能質量暫態擾動信號的小波變換。

本文在參考多種小波函數的，針對暫態擾動信號特點，決定采用Daubechise小波函數進行電能質量擾動信號的提取。Daubechise小波函數具有具有正交、時頻域支撐，具備快速速衰減的優勢，能滿足電能質量擾動信號奇異點的檢測。在參考相關文獻[21]的基礎上，對比了Daubechise系列，決定采用濾波長度系數為4的Db4系列作為電能質量問題分析。

1.2.2 分解層數的確定

合理的確定小波變換分解層數是準確提取電能質量擾動信號特征量的重點[22]。為滿足電能質量暫態擾動的時頻域暫態特性，保證基頻處于最低子頻帶中心，降低子頻帶受基頻分量的影響。本文根據信號采樣來確定小波分解層數。小波分解頻帶劃分采用式(3)。

(3)

式中：fs和f0分別為信號采用頻率和信號基頻；P為分解層數。

1.2.3 小波變換的特征提取

擾動信號經過多尺度分解成一系列相對應的系數。當對電能質量擾動信號進行l層分解后，定義小波變化在各層的能量分布為式(4)。

(4)

式中：j=1,2,…,l。擾動信號經過l層分解得到一個l維特征向量P作為向量機輸入值，即可得到式(5)。

P=[ED1,ED2…EDl]

(5)

由于上述方法獲得的擾動信號能量分布特征向量較為接近，在實際應用過程中很難進行分類，因此通常在獲得的P中減去理想電壓信號Pref，獲得二者的能量差分布特征向量ΔP作為向量機的輸入值。

1.3 電能質量暫態擾動分類

支持向量機(SVM)是將不同種類樣本通過原始空間或映射到高維空間構造成最優超平面[23]。如圖2所示。

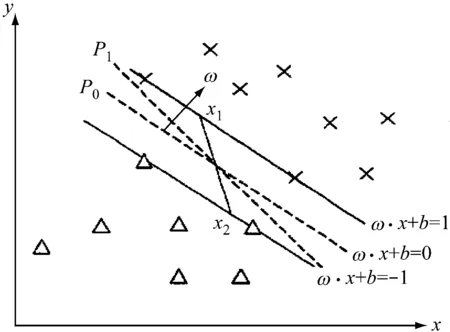
圖2 線性可分下的超平面示意圖

圖2中的兩類點分別為兩種樣本。假設樣本是線性可分的，則通過SVM獲得的學習結果是一個超平面，將獲得的超平面稱之為判別函數。根據經驗風險最小化準則，有無數個相同類型的超平面，因而能夠達到較好的分類目的，但卻不具備強度的預測推廣力。根據統計學理論結構最小化準則，通過學習獲得的最終結果應是尋找到系統的最優超平面P0，要求P0同時具備較大的分類間隔和理想的分類效果。

本文中主要是針對電網電能質量暫態擾動進行分類，因此，選擇采用多類分類支持向量機。即每個SVM分類器只針對一個電能質量暫態擾動判別，如針對電壓暫態問題，當經過分類器判定輸入波形為電壓暫升類型時，對應的分類器輸出為1，否則為0。類似的其他SVM輸入結果為0或1，最終獲得輸出向量O=[o1,o2,…ol]，理論上，只有對應的SVM輸出為1，其余均為0，當輸出向量中存在多個1時，表明該擾動為符合擾動類型。

在分類步驟可以看出，采用SVM分類中可知，用SVM作分類時需要對核函數參數g以及懲罰參數c等進行調節才能獲得較理想的分類結果。本文采取交叉驗證思想來選定最優參數。選用K-CV方法選定核函數g和最佳懲罰函數c的相關參數。具體步驟為：將g、c參數在(2-10,210)選定值；利用網格搜索法獲得相應的參數度(2-10,210)(ci,gi),i=1,2,…m,j=1,2,…n；利用K-CV交叉驗證法對參數對(ci,gi)確定分類最佳參數對(cbest,gbest)，若有多組(ci,gi)對應相同的最佳參數對，則選定最小的參數對(ci,gi)作為最佳參數；根據獲得的最佳參數對來縮小對應的g、c參數取值范圍，重新進行分類選擇直到獲得最佳參數對(cbest,gbest),電能質量擾動分類流程圖,如圖3所示。

圖3 電能質量擾動分類流程圖

2 仿真實例驗證

為驗證基于小波變換對電能質量暫態擾動信號的識別和分類準確性，本文選定電壓暫降、電壓暫升、暫態振蕩和暫態脈沖、電壓中斷五種單一電能質量暫態擾動指標和電壓中斷+暫態振動和電壓暫降+暫態振蕩的復合型電能暫態擾動信號進行分析，設計每種擾動樣本各500個，隨機選擇其中的350個樣本用于SVM分類訓練樣板，剩余150個用于樣本測試。為模擬實際噪聲，在樣本上施加了一個疊加白噪聲，經過去噪處理后采用選定的DB4小波進行10層分解，并提取信號中的特征向量，構建SVM分類器，并在基于Mathb軟件上進行仿真訓練測試。為表現一對多方法的優越性，本文分別對比分析了BP神經網絡分類器和改進的SVM分類器的訓練和測試進行了對比分析。獲得的擾動結果分類如表1所示。

從獲得的試驗結果可以看出，采用改進的SVM電能質量暫態擾動分類法的單一暫態擾動指標的平均準確了為96.5%，而采用BP神經網絡分類器的分類準確率為91.6%，同時，加入的兩種通過仿真結果對比分析可知，電壓終端+暫態振動和電壓暫降+暫態振蕩的復合型電能暫態擾動信號準確率也在94%以上，明顯優于BP神經網絡法的91%，采用改進的SVM法能有效識別電網中存在的電能質量暫態擾動。

可以看出，采用改進的SVM訓練法的訓練時間遠遠低于BP神經網絡法，因此，在分類快速性和高效性方面采用改兩種不同訓練法的訓練和測試試驗,結果如表2所示。

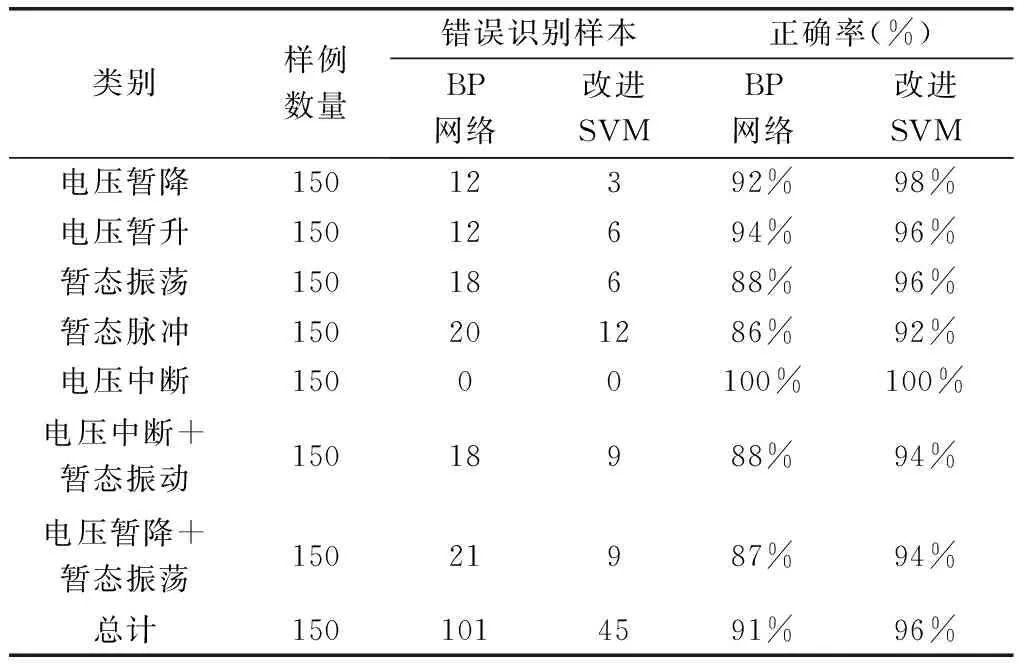
表1 電能質量暫態擾動分類結果

表2 分類器訓練測試時間

進的SVM分類法也明顯優于BP神經網絡法。

3 總結

基于電能質量暫態擾動信號的暫態多變特征，提出一種基于小波變換來實現電能質量暫態擾動信號的特征值識別和信號分類。提出一種改進的閾值函數來進行信號的分離，實現對電能擾動低頻穩定信號和高頻噪聲信號的分離；采用Daubechise 4小波函數進行電能質量擾動信號的提取。為保證基頻處于最低子頻帶中心，降低子頻帶受基頻分量的影響，利用小波分解頻帶進行擾動信號分層。并利用K-CV方法選定相關的擾動信號參數。實例驗證表明，采用本文提出的改進型SVM法能有效提高電能質量暫態擾動的分裂準確率和效率。